基于双圆弧曲线优化的玻璃切割系统
何发富,张李超
(华中科技大学 材料成形与模具技术国家重点实验室,湖北 武汉 430074)
1 动机与双圆弧的定义
1.1 曲线拟合在加工中的重要性
伺服电机与驱动器组成的半闭环控制系统,应用极其广泛。由于该半闭环控制系统不完全反馈功能会导致加工轮廓局部失真[1]。为满足加工精度要求,必然要设置额定加工速度、加速度等加工参数来限定加工。传统数控加工系统采用直线段逼近曲线会造成轮廓曲线的不连续和波动[1],轮廓的局部曲率过大也会导致机床抖动加剧、加工误差增大等现象发生。因此二维轮廓的平滑处理可以提高加工质量以及增加机床设备工作的平稳性。一些研究者基于尖点、切点、敏感点及可拟合点对曲线进行分段处理,重构优化加工轮廓以消除敏感点对加工质量的负面影响[2]。从实际应用方面来看,G1曲线的路径可以降低刀具的过切情况、降低高速加工中机床震动及提高产品成形表面质量[3]。本文对分段后的轮廓进行双圆弧曲线拟合,保证曲线的G1连续性及控制曲线的局部曲率。改善高速加工中不平稳的问题,并满足曲线拓扑结构不变的要求。
分段圆弧样条曲线[4]是工程应用的常规方法。本文的目的是使用一系列的圆弧曲线来插补轮廓,并保证圆弧曲线位于指定的容差带内。这种方法的优点:易保证曲线一阶连续、降低原始轮廓微小波动产生的干扰、减少原始轮廓数据量。根据双圆弧公共点相切的特性,指定曲线通过的节点的切线方向,即可保证拟合的双圆弧曲线一阶连续;当原始轮廓波动的振幅小于容差带的允许误差时,干扰波动可以被消除;可以使用较少的双圆弧曲线拟合轮廓,实现数据压缩。
1.2 双圆弧曲线的构造
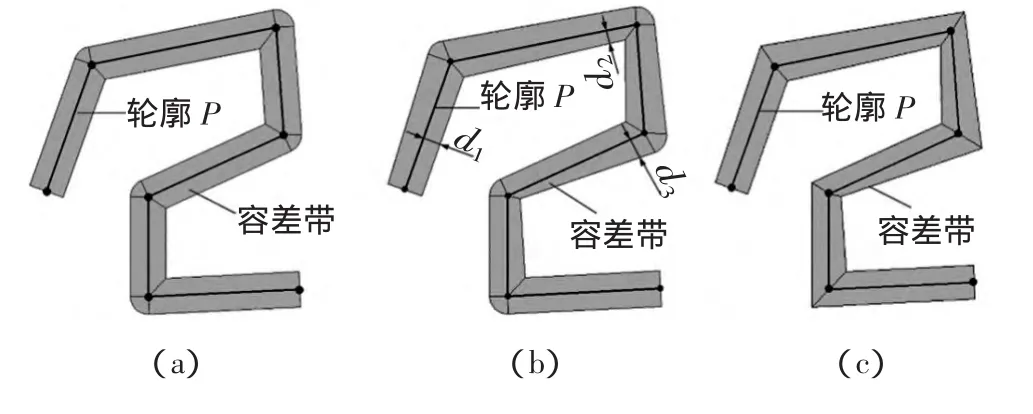
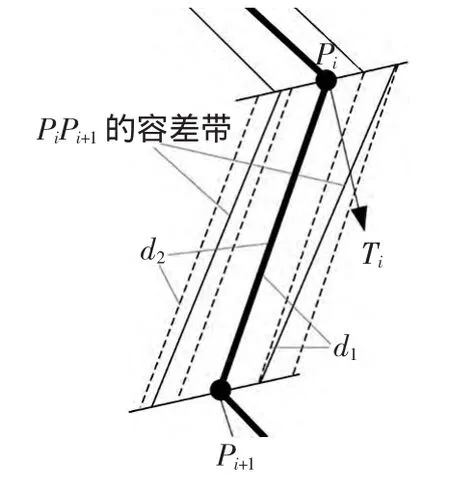
根据Bolton[5]的定义,双圆弧是一对首尾相连并且连接点切线方向相同的圆弧。杨旭静[6]对它的几何计算公式进行了推导。如图1,平面上任意两点Ps和Pe以及过这两点的单位矢量Ts和Te,存在多条首尾分别过Ps和Pe两点且首尾端单位切矢分别为Ts和Te的双圆弧,这些双圆弧形成一个双圆弧族。图1所示为双圆弧族中的一个双圆弧,Pc为连接点,V为Ps到 Pe的向量,θ1、θ2分别为 V 到 Ts、Te的夹角(顺时针方向为正,反之为负),ω1为Ts到PsPc的夹角,ω2为 PcP2到 PcPe的夹角,l=||PsPe||,ρ=||P1Pc||。设 k=||P1Pc||/||P1P2||为 Pc分割 P1P2的比例参数(0 设 ns=PsO1、ne=PeO2,圆心可表示为: 图1 双圆弧几何模型 给定参数条件k,利用上述方程便可以确定双圆弧方程及相关的几何数据信息,杨旭静[6]已经证明参数条件k与圆弧曲线的曲率是单调关系。那可通过k的取值方法不同,找出符合使用者自定义的最优条件的双圆弧。 根据行业习惯,如果θ1、θ2的符号相同,构造曲线为S型双圆弧,反之构造C型双圆弧。 基于容差带拟合双圆弧曲线,容差带直接决定了曲线的拟合精度及拓扑结构。M.Held[7]提出基于轮廓生成的四边形、扇形、扇盘形组成的k-dops的容差带算法,它维持曲线的拓扑结构稳定。为消除在轮廓“瓶颈”处容差带重叠可能会导致曲线自交现象,需要对重叠的k-dops进行紧缩处理,这一处理导致容差带过渡紧缩及算法性能问题。后来M.Held[8]再提出基于V图的生成方法计算非对称的容差带,这虽然保证了生成的曲线不会发生自相交的情况及在轮廓“瓶颈”处容差带过渡紧缩现象,但生成V图复杂性[9]使它不适用于大数据量处理及实时性要求较高的系统;杨旭静提出基于曲线偏置的局部实时容差带,但曲线的偏置本身就是一个复杂的过程,加之检测曲线与曲线的位置关系的复杂性使它存在计算复杂的缺点。本文提出一种快速生成非匀称的容差带算法,使轮廓拟合的切线连续双圆弧曲线位于容差带内,并对容差带进行优化处理,解决容差带过渡紧缩及曲线自相交拟合错误的问题。 对给定的平面轮廓(平面多边形或折线)P,根据M.Held的定义[7],包含P的区域C,如果其边缘到P的单向 Hausdorff距离 h(p,C)p∈P等于常数 ε,称 C为P的容差带,ε为P的容差带容差。对于折线,其容差带需要去掉首尾端的半圆形区域。如果一个包含P的条形区域C,其边缘到P的单向Hausdorff距离 h(p,C)p∈P小于等于常数 ε2大于等于常数 ε1,称区域 C 为 P 的非匀称容差带,区间(ε1,ε2)为 P 的非匀称容差带容差,图2b为图2a对应的非匀称容差带。 图2 轮廓P容差带 容差带的边缘轮廓由线段和相对较小的圆弧组成,圆弧的数量与线段的数量一致。对计算机来说,圆弧的处理复杂程度是线段的几倍甚至上百倍,这将消耗很多的计算机资源。本文提出了一种解决方法。称去掉小圆弧的容差带为准容差带,相应的,称去掉小圆弧的非匀称容差带为准非匀称容差带,图2a对应的准非匀称容差带如图2c。大量的实际结果表明,准容差带与容差带对双圆弧曲线的约束效果一致,因此在下文将使用准容差带来代替容差带。 定义1:线段端点沿线段法向的偏移距离为线段的端点容差距离εe,线段端点沿端点切线法向上的偏移距离为线段端点法向容差距离εv。轮廓P一般容差带的线段端点容差距离εe等于容差ε,非均匀容差带的线段端点容差距离εe与容差区间(ε1,ε2)满足关系式:ε1≤εe≤ε2。 基于李敏[2]对多边形或折线轮廓的预处理方法,将轮廓分割为多段可拟合的轮廓段。一段可拟合的轮廓段P,其离散点Pi(i=1,2,…,n),设P的一般容差带容差为ε,非均匀容差带的容差ε1=0.5ε、ε2=ε,其非均匀准容差带的计算方法如下: (1)计算节点Pi的切矢Ti(1≤i≤n)。非封闭的轮廓端点节点切矢使用G.H.Liu[10]的方法构造。取端点及相邻点 P1、P2、P3,令 A=P2-P1,B=P1-P2,C=A×B,那么 P1的单位切矢T1=D×C/‖D×C‖,其中 D=(‖A‖2(B×C)+‖B‖2(C×A))/2‖C‖2,非端点节点使用平行向量法[11]求其单位切矢; (2)如图3,预测相邻节PiPi+1生成双圆弧的形状,确定线段PiPi+1的非均匀容差带的容差带。已知节点 Pi、Pi+1及曲线切矢 Ti、Ti+1,可预测双圆弧曲线类型。如果为C型双圆弧曲线,则紧缩曲线凹侧的端点容差距离,如紧缩后的端点容差距离为ε1,凸侧端点容差距离不变。如果为S型双圆弧曲线,则根据切矢与线段的夹角比例系数 k(k=min(|θ1/θ2|,|θ2/θ1|),0 (3)整合所有轮廓线段的容差带,得到最终的容差带。对于节点Pi(i=2,3,…,n),其非均匀端点法向容差距离分别在线段Pi-1Pi和线段PiPi+1的容差带中计算了两次,由于两次计算的值不可能完全一致,这必然导致线段Pi-1Pi和线段PiPi+1的容差带在节点Pi处出现断裂。为了消除这种断裂现象,本文将取端点法向容差距离较大的值来重新计算容差带的坐标,得到轮廓的一个连续非均匀容差带。 图3 节点Pi、Pi+1的生成的容差带d1=ε1<ε2=d2,(ε1,ε2) 为轮廓 P 的非匀称容差带容差区间 可拟合的轮廓P,其离散点Pi(i=1,2,…,,n)。取P0Pn进行拟合,如果拟合的双圆弧曲线包含于轮廓P的容差带,拟合结束,否则将对P0P(n/2)和 P(n/2)Pn进行拟合,直到拟合成功。如果这个过程中存在某两相邻节点PiPi+1(1≤i 图4 容差带的整合,取节点处εv较大的值作为目标距离。 如图5所示,轮廓存在一些所谓“瓶颈”的现象,“瓶颈”处的容差带出现重合,在曲线拟合时可能会出现曲线自交现象,改变轮廓的拓扑结构,这在工程中是致命的错误,这直接使加工件报废甚至会损坏机床。为了避免这轮廓“瓶颈”处的拟合错误,本文将提出一种有效的解决方法。 图5 容差带去重叠-拟合曲线与原始轮廓拓扑结构一致 曲线自交的必要条件是容差带的重叠,那么解决曲线自交的有效办法就是消除容差带的重叠现象,也即是对容差带进行去重叠化处理。简单而有效的方法就是把重叠区域从中间分割,这样容差带永远只可能相接而不会重合,根据拟合中曲线必须在容差带内的这一条件,保证了拟合后的曲线不会发生自相交的情况。如图6a是去容差带去重叠化后的拟合结果。 本文提出的基于轮廓非均匀容差带的双圆弧拟合算法,已经实现并集成到玻璃切割系统的二维轮廓优化处理模块中,在南京烨拓自动化设备有限公司的自动化球面玻璃切割设备中成功应用。使设备的加工速度由原来的6.5m/min提高到10m/min,加工面的粗糙度也明显得到改善。 图6 容差带去重叠-拟合曲线与原始轮廓拓扑结构一致 由于水刀玻璃切割适合厚板慢速切割[12],常规玻璃都采用金刚石刀头进行切割。由于玻璃易碎、硬度高等特性,决定了其加工过程中不能有太大的震动,否则刀具容易被损坏,同时加工面将很粗糙甚至产品报废;再者,刀具与毛坯表面的接触力要均匀且适中,接触力过小会导致割痕浅,以至后续加工失败,接触力过大产生的深割痕难以在后续加工中去除,影响加工质量。由此,为减小报废率,玻璃切割设备必须运行平稳,切割轮廓路径需平滑。 为了达到轮廓平滑的要求及设计方便,玻璃切割轮廓一般由直线、圆弧及Nurbs样条曲线组成。在玻璃切割领域,轮廓基本是根据需要反求而来,这个过程容易导致轮廓在曲线与曲线的连接处切线微小的不连续,极大的限制了加工速度及加剧了机床的震动,这就需要在后续进行平滑重构处理。 目前数控系统不支持Nurbs样条曲线,通常的方法是使用线段来插补样条。本文采用线段来插补轮廓,然后再使用双圆弧来拟合线段轮廓,由于拟合后的双圆弧曲线G1连续,即可实现重构后的轮廓平滑。图7展示了重构后局部轮廓的平滑效果,图7a中圆圈处轮廓存在微小的不连续,这些不连续很微小,重构后的曲线在链接处切线连续,实现消除原始轮廓微小切线不连续的缺陷。 图7 重构消除了原始轮廓的不平滑 重构的另一个方面可以大大的减少轮廓的数据量,原始的方法是使用短线段及圆弧来标示轮廓,从局部上来看,在误差允许范围内,多条线段可以使用一个圆弧来表示,使用双圆弧重构的方法是可以极大限度的使用最少的圆弧数量来表示原始轮廓,实现数据压缩。图8所示轮廓的原始线段和圆弧的数量为554,重构后的圆弧数量为31,图中轮廓上的小黑点为圆弧与圆弧之间的连接点。大量的实验室数据表明重构对原始轮廓的数据压缩比例约为1%~20%。 图8 重构后圆弧数量大大减少 重构的稳定性也可以通过容差带的去重叠化处理得到保证。重构后的轮廓的拓扑结构保持与原始轮廓的拓扑结构一致,保证重构后的在轮廓“瓶颈”处不会发生自相交情况。容差带在轮廓“瓶颈”处发生重叠,拟合的曲线虽然都在轮廓对应的容差带内,但不能保证曲线在容差带的重叠区域放生自交,改变轮廓的拓扑结构。实验结果证明算法可以有效的把重叠区域相对平均的分配给竞争区域,实现容差带相邻而不重叠,保证拟合曲线不会出现自交拟合错误,保证拟合曲线与原始轮廓拓扑结构一致。 对有n个离散节点的轮廓,算法计算节点切矢、准非匀称的容差带的时间复杂度分别为O(n)、O(2n)。假设相邻节点的双圆弧曲线都在容差带内,最坏情况下,算法拟合曲线的时间复杂度为O(log2n),总时间复杂度为O(log2n+3n)。表1显示了算法在拟合曲线的各个阶段的时间消耗,从表中数据显示,算法的复杂度为线性的,对处理数据量比较大的轮廓也非常快,重构不会成为系统处理轮廓的瓶颈。 表1 时间消耗 表中时间时间t(单位为ms),拟合n个节点轮廓的双圆弧曲线,轮廓的容差带容差为(0.05,0.1)。合计的时间包括了轮廓节点的前期处理。实验平台:Windows NT系统,intel 1.7GHz处理器,4GB内存。 经使用双圆弧拟合技术进行平滑重构后的2D轮廓,投影到球面上的三维加工路径依然是一阶连续的。应用平滑处理技术后,原来的玻璃切割设备的加工效率得到大大的提高,在没有使用双圆弧拟合技术前,当加工速度超过6.5m/min时,机床会发生明显的震动及加工质量下降问题,使用双圆弧拟合技术平滑处理轮廓后,加工速度可以提高到10m/min,加工质量也明显得到改善,图9展示使用双圆弧拟合技术前后的加工件质量。 图9 双圆弧拟合平滑处理,改善加工质量 本文针对伺服控制器加电机的半闭环控制加工设备,为解决存在的运动不平稳、加工质量粗糙问题,提出并实现了一种对二维轮廓重构优化的平滑处理技术。采用一种基于轮廓容差带控制曲线拟合误差的双圆弧拟合算法对可拟合轮廓段进行平滑处理,并满足拟合曲线与原始轮廓拓扑结构一致,有效的控制曲线拟合误差,实现了加工轮廓的G1连续。通过加工对比试验发现:二维轮廓经平滑处理后,加工效率显著提高,零件质量显著改善,轮廓更加光顺,误差更小,很好地解决了机床抖动频繁影响运动平稳性的问题,验证了本文提出的平滑处理算法是合理可行的。 [1]王海涛,赵东标,高素美.参数曲线的自适应实时前瞻插补算法[J].计算机集成制造系统,2010,16(2):385-389. [2]李 敏,张李超,莫健华.一种数控加工二维轮廓的平滑处理技术[J].计算机集成制造系统,2011,12(17). [3]刘爱林.片材叠层制造中若干关键技术的研究[D].武汉:华中科技大学,1999. [4]杨雨牲,赵晓东.一种简便的圆弧样条曲线拟合方法及计算[J].锻压机械,1996,2:51-52. [5]Bolton KM.Biarc curves[J].Computer Aided Design,1975,7(2):89-92. [6]杨旭静.自由曲面高性能数控加工刀具路径技术研究[D].湖南大学博士学位论文,2006. [7]M.Held,J.Eibl.Biarc approximation of polygons within asymmetric tolerance bands[J].Computer Aided Design,2005,37(4):357-371. [8]M.Heimlich,M.Held.Biarc approximation,simplification and smoothing of polygonal curves by means of Voronoi-based tolerance bands[J].International Journal of Computational Geometry and Applications,2008,18(3):221-250. [9]Oswin Aichholzer,Wolfgang Aigner.Divide-and-conquer for Voronoi diagrams revisited[J].Computational Geometry,2010,43:688-699. [10]G.H.Liu,Y.S.Wong,Y.F.Zhang,H.T.Loh.Adaptive fairing of digitized point data with discrete curvature.Computer-Aided Design,2001,34:309-320. [11]张三元,伍家凤,梁友栋.3D数据点列的双圆弧样条插值[J].浙江大学学报(理学版),2000,27(5):540-543. [12]温效康,宋拥政,梁志强.高压水切割技术的试验研究[J].锻压机械,1994,29(5):15-19.
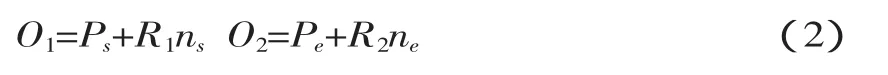

1.3 双圆弧拟合算法的发展
2 双圆弧拟合算法的实现
2.1 非匀称容差带的定义
2.2 非均匀准容差带的生成
2.3 双圆弧曲线拟合

2.4 容差带的优化

3 在玻璃切割系统中的应用

3.1 玻璃切割设备及加工轮廓要求
3.2 轮廓的平滑化重构



3.3 加工质量

4 结束语

