闭式压力机组合机身数值模拟与试验研究
詹俊勇,仲太生,高建和
(1.江苏扬力集团有限公司,江苏 扬州 225127;2.扬州大学,江苏 扬州 225127)
由于压力机向大型化、重型化发展,越来越多的闭式压力机采用组合式机身。与整体机身相比,组合机身不仅可使压力机的承载能力提高,而且具有结构紧凑、刚度大、重量轻、制造难度低、方便运输等特点。其结构由横梁、立柱及底座三部分构成,各部件之间由拉紧螺杆通过液压螺母施加预紧力连接成一个整体,机身空载时处于一种预应力状态,施加工作载荷后机身各部分的结合面始终保持紧密接触,不能出现间隙和错位[1-2]。
传统的对闭式压力机组合机身结构的研究,多是将机身各部件进行简化并且连接在一起进行计算[3-4],忽略各部件的接触关系。随着组合式预应力机身研究的深入,这种简化对压力机机身的研究结果是有影响的[5-6],不能正确反映组合式机身各部件的实际接触状况,且无法有效施加合适的预紧力,最终影响计算结果准确性。
因此,本文利用接触力学闭式压力机组合式机身进行分析,并结合有限元模型对闭式压力机组合式机身的预紧力进行研究,并将有限元计算的结果与试验所得结果进行验证,以确保计算结果的可靠性。
1 闭式压力机组合机身接触界面分析
1.1 接触界面
闭式压力机组合机身的横梁与立柱、上液压螺栓端面,底座与立柱、液压螺栓端面之间的接触区域存在接触的界面定义为接触界面,接触界面存在着非线性,其非线性来源于两个方面:一方面,接触界面的区域大小和相互位置以及接触状态事先未知,且随时间变化,需要在求解过程中确定;另一方面,接触条件是非线性的,为单边性的不等式约束。该接触问题中各接触界面的接触行为为有摩擦接触,采用库仑摩擦模型分析界面摩擦问题E。各部件的接触状况在工作时是未知的,存在着3种接触状态,即分离状态、有相对滑动的滑动接触状态、无相对滑动的粘结接触状态[7-8]。
当预紧力足够抵抗工作载荷和振动时,机身的接触状态为粘结。当预紧力不足以抵抗工作载荷和振动,各部件之间会产生间隙和错移,接触状态为分离或者滑动状态。
1.2 接触边界条件
接触界面可能出现3种接触状态,其相应的定解条件和校核条件E分别为粘结、滑动和分离[9-10]。
1.2.1 粘结
定解条件:

校核条件:
1.2.2 滑动
定解条件:

校核条件:

若不满足,转为粘结,若满足,则搜寻新的接触位置。
1.2.3 分离
定解条件:
t+ΔtFNA=t+ΔtFNB=0,为无接触力作用自由边条件。
校核条件:
(t+ΔtxA-t+ΔtxB)gt+ΔtnTB>εd,若不满足,则转为粘接。
上述3种条件中用A、B代表两个相互接触的接触面,定义A为接触体,B为目标体;N、T分别代表法向分量、切向分量;u为位移;μ为摩擦系数;ε为避免小量误差而规定的某个小量。此处不区别动静摩擦系数,假设,μd-μs=μ,g代表两接触点的距离,F代表接触力。
1.3 接触问题的增量描述及变分求解
1.3.1 接触问题的增量理论分析
接触过程依赖于时间,接触界面的区域和形状以及接触界面上运动学和动力学状态是事前未知的,故采用增量方法求解此类接触问题E。材料与时间t+△t位形内物体的平衡条件及力边界条件相等效的虚位移原理可表示为:
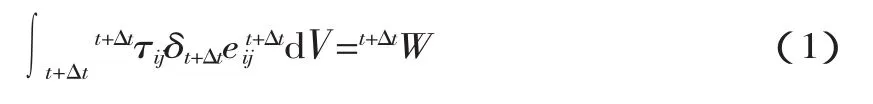
式中:t+ΔtW——时间t+Δt位形的外载荷虚功。

由于式(1)t+Δt位形未知,因此采用更新拉格朗日格式进行位移增量ui求解,该格式中所有变量以时间t的位形作为参考位形。得到增量求解的非线性表达式为:

将式(3)线性化处理得到:
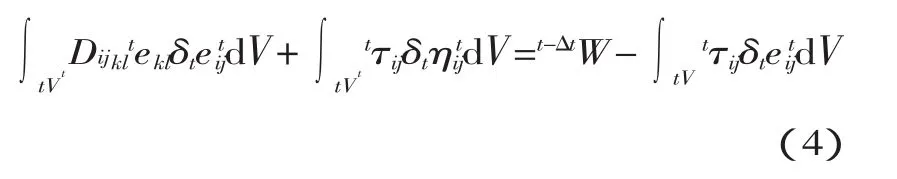
以上述方程变分的结果得到关于位移增量ui的线性方程组。
式(1)~(4)中t+Δtτij是时间 t+Δt位形的欧拉应力,δ、e分别代表真应力和真应变的瞬时变化率。S、V、ρ分别代表表面积、体积及质量密度。
1.3.2 变分法求解位移增量的方程
为将接触边界条件引入接触方程,利用拉格朗日乘子法将附加约束条件引入泛函求解关于位移增量的线性方程组,其泛函表示为:
∏=∏u+∏CL
式中:∏u——原问题中不包括接触约束条件的总位能;
∏CL——用拉格朗日乘子法引入接触约束条件的附加泛函。
对于不同的接触条件引入相应的边界条件,用泛函的变分,令δ∏=δ∏u+δ∏CL=0得到求解方程。
(1)粘结接触状态虚功表达式

接触面上t+ΔtSCA和t+ΔtSCB上的接触力为

(2)摩擦滑动接触状态虚功表达式

对于拉格朗日乘子λN,求解时需补充法向不可贯入约束条件:

2 拉紧螺杆预紧力分析
压力机在工作时,横梁、底座和立柱之间不得产生间隙和错位,为此必须给拉紧螺栓以预紧力,使机身受压,有一定的预压缩量,同时拉紧螺栓相应受拉,有一定伸长量。当工作时,机身的预压缩量减小,螺栓进一步伸长。通常因横梁和底座的截面很大而高度较小,对于立柱而言,其压缩量可忽略不计。故对机身变形只是考虑立柱的变形。图1是拉紧螺栓和立柱的变形情况简图[2]。

图1 螺栓和立柱变形示意图
由图1,如设λl为预紧后拉紧螺栓伸长量,λz为预紧后立柱压缩量,λl′为工作时拉紧螺栓的伸长量,λz′为工作时立柱残余压缩量,则拉紧螺杆在压力机工作时比预紧时所增加的伸长量为Δλl=λl′-λl,立柱在压力机工作时比预紧时所减少的压缩量为Δλz=λz′-λz。由 Δλl=Δλz=Δλ 得:

在弹性范围内,螺栓和立柱的受力和变形都是线性的,如图2表示。
机身受到公称力Pg作用时,拉紧螺栓除承受立柱给它的反作用力(即立柱的残余预紧力)以外,又多加了机床的公称压力Pg,所以此时螺栓受力从Py增为Pl,而立柱受力从Py减为Pz(Pz为残余预紧力)。
由图可知

此时相应的变形量,螺栓从λl变为λl′,立柱从λz变为 λz′。

图2 螺栓和立柱的力-变形图
施加预紧力的目标是要使得横梁、立柱和底座之间不产生间隙,即立柱的变形量为零,若将工作压力增至 ZPg(Z 称为预紧系数),使得 λz′=0,则立柱的变形量变为零。
则式(9)为

根据虎克定律

式中

同理

把上述诸式代入式(10)得

3 数值计算
在三维软件中建立闭式压力机组合式机身模型[10],按照有限元分析的要求对其进行适当的简化,组合式机身中横梁、立柱、底座的材料为Q235-A,拉紧螺杆材料为40Cr,机身工作台的材料为HT250,为保证模型特征的完整性,已取得最佳的计算结果,本文不选用传统对称分割三维模型的方法,而采用整机模型作为计算模型,如图3所示。
将闭式压力机机身导入到有限元软件,横梁与立柱、液压螺栓端面之间,底座与立柱、液压螺栓端面之间的接触区域定义为“Face to Face”接触,接触面摩擦系数为0.15。在拉紧螺杆中部设置预紧力单元,将预紧力定量施加于预紧力单元可使整个机身受到预应力作用。机床在工作时承受两个方向相反、大小相等的载荷,一个是作用在曲轴支撑孔上,方向朝上;另一个作用在工作台上,方向向下,机身重力加速度为9806.6mm/s2。曲轴安装孔上的作用力和工作台上的载荷分别是以均布面载荷的形式作用于机身上,同时给机床的拉紧螺杆上加上预紧力载荷。认为地基为刚性固定平面,压力机机座通过地脚螺栓与地基相连的部分6自由度全约束。

图3 闭式压力机组合式机身模型

图4 闭式压力机组合机身边界条件示意
对模型进行求解,求得机身等效应力云图与等效变形云图如图5、6所示。

图5 闭式压力机组合等效应力云图

图6 闭式压力机组合等效变形云图
4 压力机的试验
试验内容主要包括应力测试与变形测试。应力测试主要对闭式压力机进行静态测试,测试压力机在最大静载下的全场应力分布情况;变形测试是测试压力机在最大静载下机身工作台的变形[11-12]。
测试仪器选用YE2539高速静态应变仪,测试精度为 1με,测试范围 0~±19999με;CWY-DO 位移传感器测试测试精度0.01mm,测试范围10mm;Br120—2AA电阻应变片。CRAS V7.0振动及动态信号采集分析系统,采集精度0.0001m/s2;AZ308数据采集系统,KD6005应变放大器。
应力测试的主要内容是:根据压力机机身的受力分析,在均匀应力区、应力集中区、弹性挠曲区等危险应力区选取适当的应力测点,粘贴上电阻应变片。测试中将电阻应变片与静态应变仪连接,模拟实际工况给压力机加载,再在计算机上通过软件将各测点的应变值采集下来。变形测试的主要内容是:将位移传感器布置在机身工作台上,再将位移传感器经数据采集系统连接到计算机,模拟实际工况给压力机加载,通过振动及动态信号采集分析系统软件进行数据采集。

图7 应力测试

图8 变形测试
由应力测试结果可知,绝大部分测点应力不超过40MPa,机身工作台最大变形发生在工作台中部,变形量达到0.671mm,测试结果与有限元分析结果基本吻合,误差在15%以内,见表1所示。
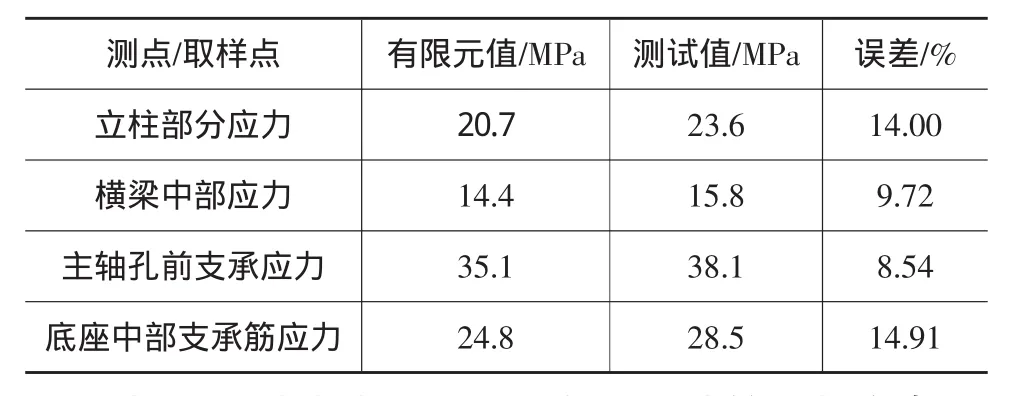
表1 机身受载时各主要测点与有限元计算取样点的数值比较
由变形测试结果可知,有限元计算的机身角变形值与实测值基本吻合,如表2所示。
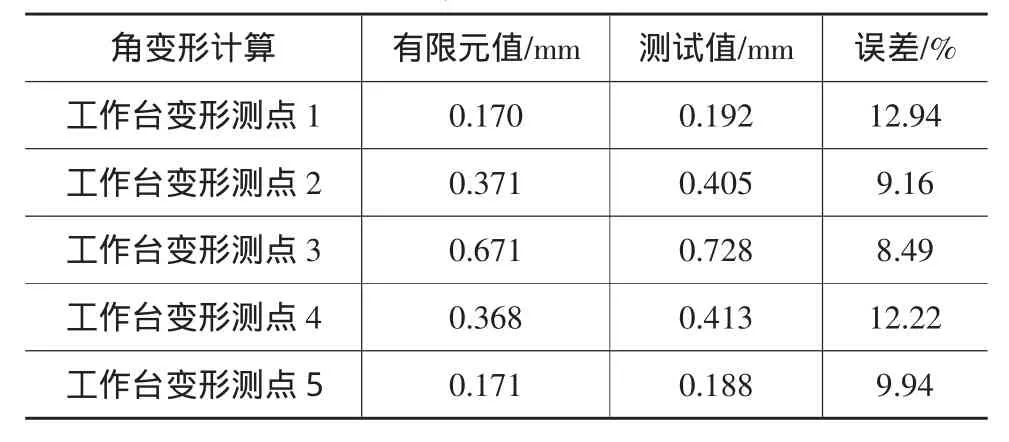
表2 机身受载时实测的变形值与有限元计算值的比较
5 结论
(1)对闭式压力机组合机身的接触问题进行分析,合理定义各部件之间的接触,施加合理预紧力可以获得较为准确的计算模型。
(2)合理定义闭式压力机组合机身计算模型的边界条件,可以获得较为准确的计算结果。
(3)通过有限元分析和结构试验相结合的方法对闭式压力机组合机身做了细致的分析对比,有效避免了因单独进行有限元计算或结构测试带来的误差,提高了分析结果的可靠性,同时证明了分析方法的可行性。
[1]范宏才.现代锻压机械.北京:机械工业出版社,1994:52-53.
[2]何德誉.曲柄压力机.北京:机械工业出版社,1951:129-152.
[3]李德军,李培武,管延锦,等.22MN液压机整体框架式机身的有限元分析[J].塑性工程学报,1995,2(3):55-62.
[4]沈炜良,金 红,陈 玮.高速压力机组合机身的有限元分析[J].现代制造工程,2004,(5):56-57.
[5]吴生富,聂绍珉,等.大型锻造液压机全预紧机架的整体性分析[J].燕山大学学报,2006,30(2):143-146.
[6]吴生富,金 淼,等.大型锻造液压机全预紧组合机架的整体性及影响因素分析[J].塑性工程学报,2006.13(2):1l0-l13.
[7]樊瑜瑾,杨晓京,等.磨粒磨损中微观接触过程的有限元分析[J].机械工程学报,2005,41(4):35-37.
[8]K L Johnson,徐秉业.接触力学[M].北京:高等教育出版社,1992:368-369.
[9]叶 红,颜廷武,刘元胜.法兰连接中的螺栓预紧力[J].有色矿冶,2005,21(3):46-48.
[10]詹俊勇,黄建民.SolidWorks导入实现ANSYS参数化建模[J].金属加工,2010,4:71-72.
[11]詹俊勇,黄建民.JH21-63型压力机机身的有限元分析与结构测试[J].锻压装备与制造技术,2010,45(2):61-63.
[12]叶 亮,高建和,田万英,等.激光切割机横梁的模态特性分析[J].扬州大学学报(自然科学版),2009,2:75-78.

