不同侧向入口旋风分离器流场数值分析
陈启东,左志全
(1.常熟理工学院,江苏常熟 215500;2.常州大学,江苏常州 213016)
不同侧向入口旋风分离器流场数值分析
陈启东1,左志全2
(1.常熟理工学院,江苏常熟 215500;2.常州大学,江苏常州 213016)
利用雷诺应力模型(RSM)对直切单入口、直切双入口、斜切单入口、斜切双入口、斜切螺旋面单入口、斜切螺旋面双入口6种不同侧向入口旋风分离器内部气相流场进行了计算分析。结果表明:双入口结构旋风分离器内部压力场和速度场具有更好的对称性与稳定性;仅改变入口斜切角度对旋风分离器内部速度场和压力场的分布影响不大;当本文中6种分离器内部具有相近的切向速度径向分布时,斜切螺旋面入口结构分离器压力损失减少约25%,入口所需总压降低17%,处理相同气体量的能耗约下降17%;斜切螺旋面双入口(XS-L型)分离器是一种综合性能比较优的旋风分离器。
旋风分离器;侧向入口;压降;入口总压;能耗
1 前言
旋风分离器现在已经广泛应用于化工、石油、矿山等工业部门,旋风分离器的结构也呈现出多样性。结构多样性体现之一就是入口结构多样性,很多学者专家对不同入口结构的旋风分离器进行了数值计算分析,王振兴等[1]的研究成果表明,矩形入口长宽比为1.5时压降最低,对粒径小于2.5 μm的颗粒,圆形入口分离效果最差,梯形入口分离效果最好;钱付平等[2]的研究阐述了不同入口截面角旋风分离器的分离特性,最后得出入口具有一定截面角则有利于颗粒分离;吴彩金等[3]研究了斜切双入口旋风分离器流场,发现本结构能够很好地改善单入口旋风分离器流场的不对称性,同时减小内部局部涡流。
在此基础上,本文对入口截面为矩形的直切单入口旋风分离器(ZD型)、斜切单入口旋风分离器(XD型)、直切双入口旋风分离器(ZS型)、斜切双入口旋风分离器(XS型)、斜切螺旋面单入口旋风分离器(XD-L型)、斜切螺旋面双入口旋风分离器(XS-L型)等6种不同侧向入口旋风分离器在不同入口流速下的流场进行计算,对比分析6种分离器内压力分布与速度分布,找出不同侧向入口结构对流场分布的影响。
2 数值计算模型
根据以往学者研究结果[4~6]可知,由于雷诺应力模型摒弃了各向同性的涡黏假定并且更加严格地考虑了流线弯曲、旋涡、旋转和张力快速变化,能够很好地预测分离器内部的强制涡与自由涡,计算结果与实验测量值也最吻合,所以本文计算采用雷诺应力模型(RSM)。RSM模型可以参考文献[7]。
利用ICEM软件采用六面体网格对本文中的模型进行网格划分。借用商业软件Fluent对旋风分离器内部气相流场进行数值计算。求解器选择基于压力的求解器,采用非稳态计算[8],时间步长1E-4 s[9],计算方法采用SIMPLIC算法,压力采用PRESTO离散格式,动量采用二阶离散格式,湍动能、湍动能耗散率采用QUICK离散格式,其他采用默认格式。
3 几何模型与边界设置
3.1 几何模型
本文计算采用的物理模型,双入口旋风分离器的入口高度是单入口旋风分离器入口高度的一半,排气管底端与入口底端对齐,不同单入口分离器入口高度和宽度分别相同,不同双入口分离器入口高度和宽度分别相同,其他尺寸都相同。本文中ZD型模型采用参考文献[10]中模型,结构尺寸如下(单位:m):D=0.19,a=0.038,b=0.095,de=0.064,s=0.095,h1=0.285,h2=0.475,d0=0.072 5。旋风分离器的物理模型如图1所示。
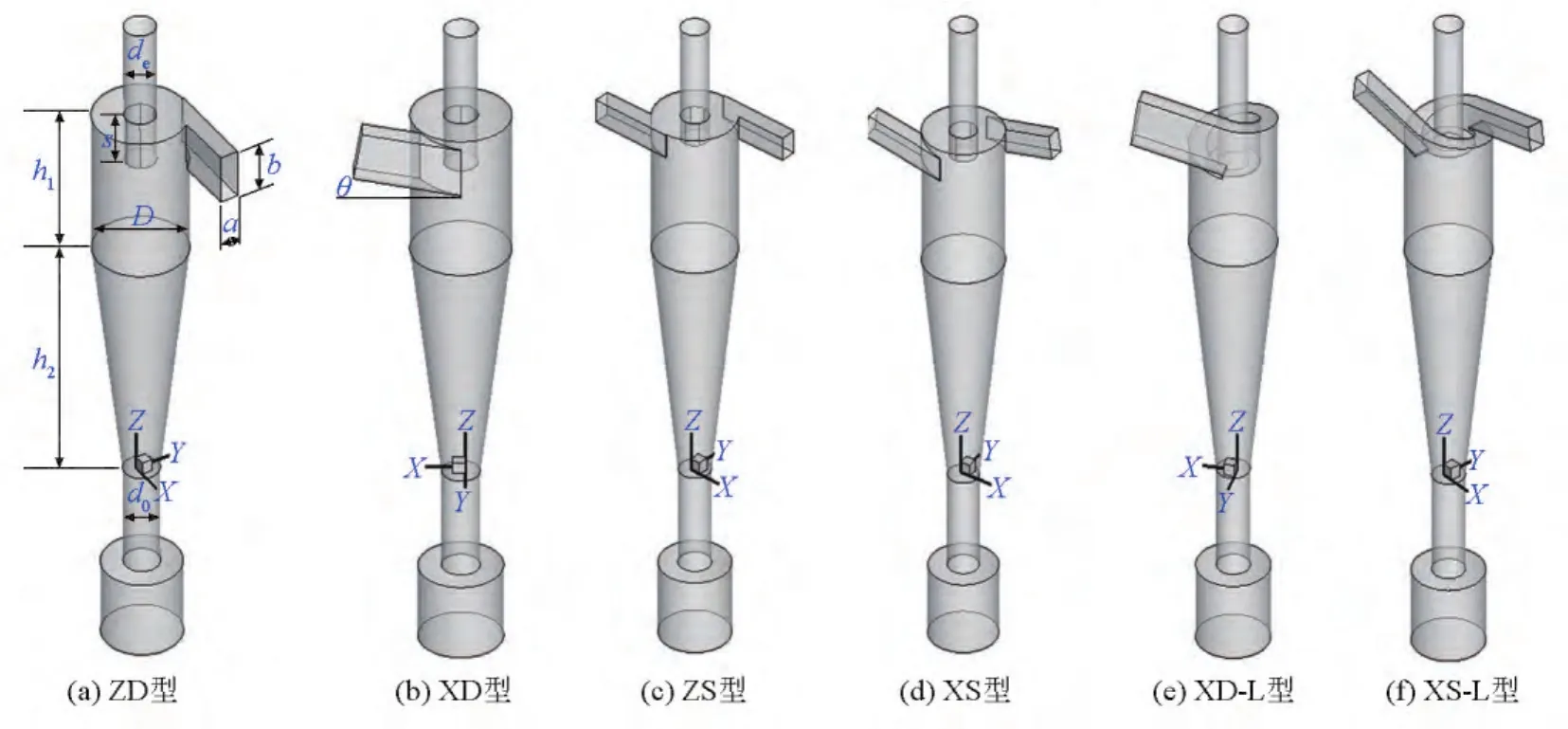
图1 旋风分离器物理模型Fig.1 Geometry of cyclone
3.2 边界条件设置
1)入口采用速度入口(velocity-inlet)。
2)排气口采用压力出口(pressure-outlet)[11],静压为0。
3)壁面采用无滑移边界,近壁采用标准壁面函数处理。
4 计算结果分析
4.1 计算模型和设置适用性验证
为了验证数值计算模型和设置的合理性以及计算结果的可靠性,本文利用前述数值计算模型和设置计算文献[10]中所给模型3个横截面上的切向速度和轴向速度,并与文献[10]中实验所测结果进行比较,如图2所示。比较结果显示,运用本文数值计算模型和设置计算出来的切向速度和轴向速度能够较好地吻合文献[10]中实验测得的数据。在切向速度径向分布上捕捉到了切向速度随径向距离增加而增大的内部强制涡以及切向速度随径向距离增加而减小的外部自由涡的Rankin组合涡的分布特点,除此,在轴向速度径向分布上还捕捉到了旋风分离器内壁面附近下旋流、中心区域上旋流的双涡运动结构,并且内外旋流的交接面位置与实验测得的结果基本一致。上述比较结果说明,本文采用的数值计算模型及相关设置适用于后面旋风分离器内部流场计算。
4.2 不同入口斜切角XD型分离器分析
对比了入口斜切角分别为5°、10°、15°、20°、25°的分离器在进口为7.5 m/s的流速下的切向速度和轴向速度的径向分布。随着入口斜切角的增大,切向速度在强制涡区域内径向分布几乎没有变化,在自由涡区域,切向速度随着入口角度增大而减小;轴向速度随着入口斜切角度的增大而增大,在靠近壁面的下旋流中,轴向速度径向分布相差不大,在中心区域的上旋流中,入口角度越大,轴向速度径向分布相差越大。靠近壁面的轴向速度小一点,有利于延长颗粒的分离时间,靠近中心附近的上旋流轴向速度对颗粒分离的影响不明显,如图3所示。
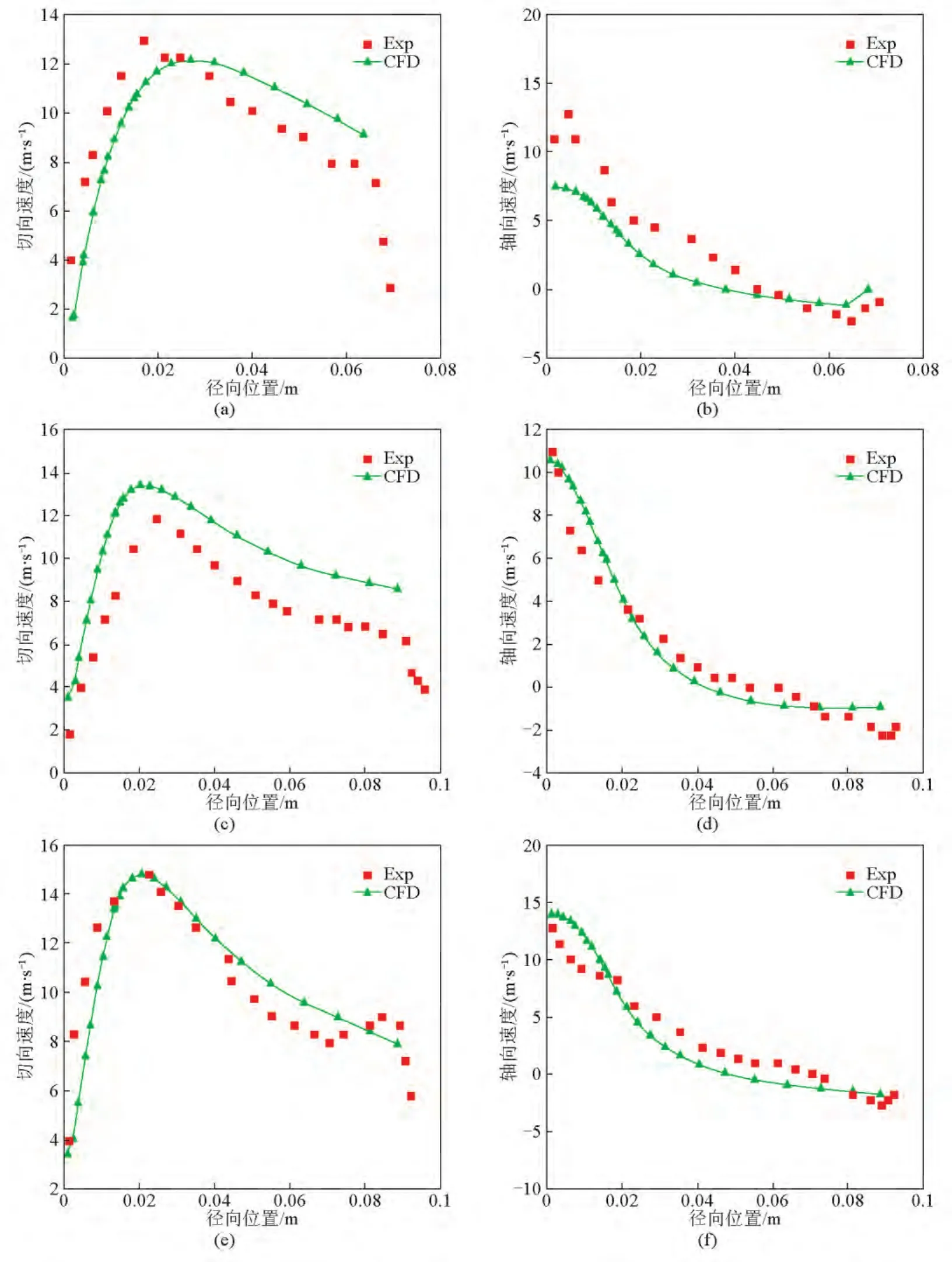
图2 旋风分离器内不同轴向位置上切向速度、轴向速度CFD计算结果与文献[10]中LDA测量结果比较(从上到下横截面为z=0.26 m,0.56 m,0.635 m)Fig.2 Comparison of the time averaged tangential and axial velocity between the RSM simulations and LDA measurements[10]at different axial sections(from top to bottom:sectionz=0.26 m,0.56 m,0.635 m)
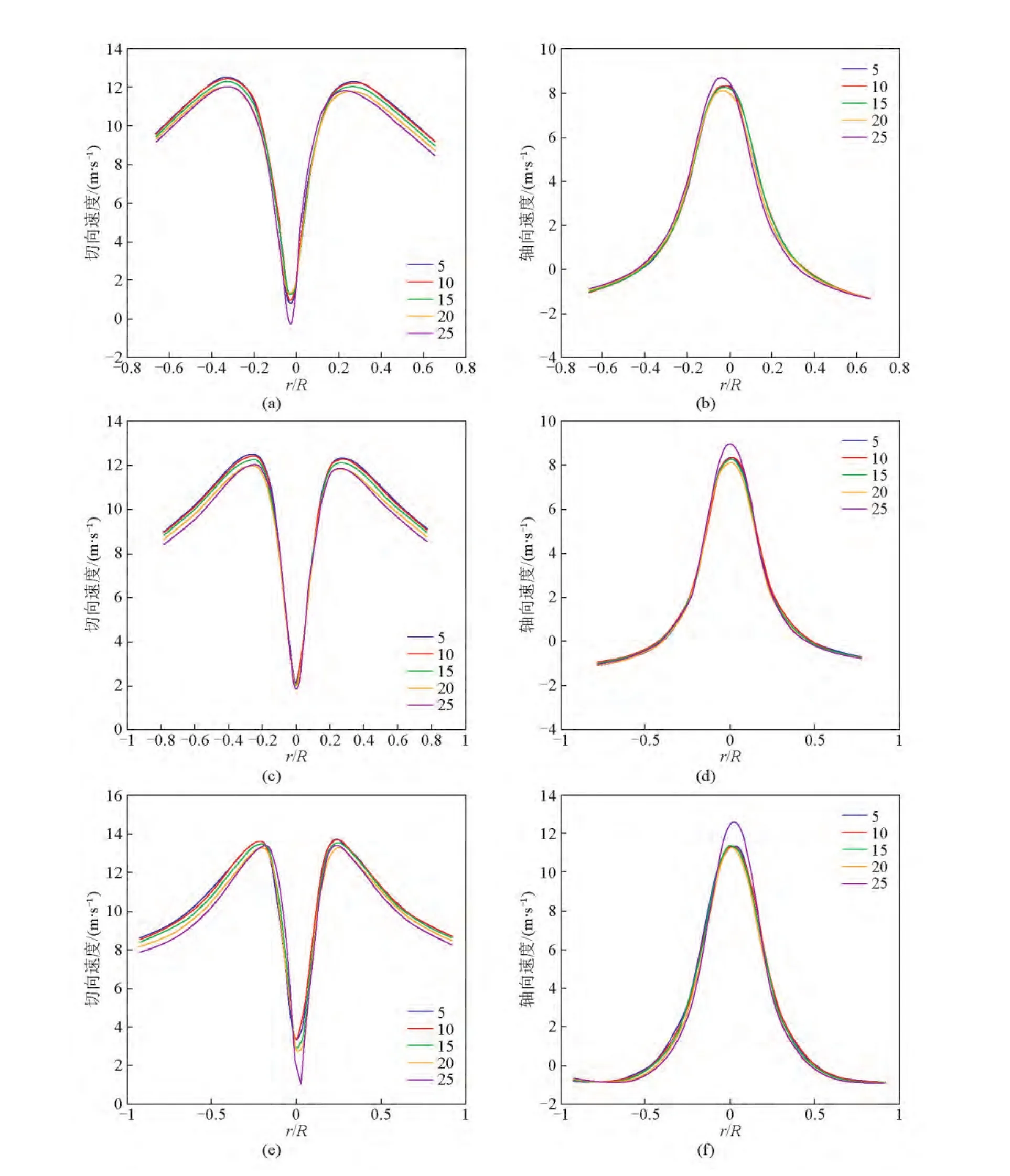
图3 不同入口斜切角XD型分离器3个横截面上切向速度、轴向速度径向分布(r为径向位置,R为筒体半径;从上到下横截面为z=0.26 m,0.36 m,0.56 m)Fig.3 The radial profile for the time averaged tangential and axial velocity at different sections for different inlet angle cyclone XD(r is the radial distance,R is the cyclone radius;from top to bottom:sectionz=0.26 m,0.36 m,0.56 m)
图4给出了分离器入口总压及压降随着入口斜切角度增大的分布。从图4可得出,随着入口斜切角度的增大,入口总压和压降都在减小。与入口角度为5o的分离器相比,入口斜切角为10o的分离器内切向速度分布曲线与之相差很小,两者几乎重合,入口总压低0.7%,压降低1%;入口角度为25°的分离器内自由涡区域切向速度分布曲线比之要低0.5~1 m/s,占入口角度为5°的分离器内切向速度峰值的6%左右,入口总压低7.3%,压降低8.8%。综合对比得出,增大入口斜切角度有利于减阻,降低压降,但效果有限,与此同时会减小自由涡区域切向速度,减弱分离效果。因此,本文所列的几个入口倾斜角度中,入口倾斜角为10°的入口结构相对较优。

图4 不同入口斜切角XD型分离器入口总压、压降Fig.4 The inlet total pressure and the pressure drop for different inlet angle cyclone XD
4.3 不同侧向入口分离器对比分析
本节对ZD型、XD型(入口斜切角为10°)、ZS型、XS型(入口斜切角为10°)、XD-L型、XS-L型6种不同侧向入口结构分离器内压力场与速度场进行分析讨论。
4.3.1 压力分布分析
图5给出了6种分离器在入口流速为7.5 m/s下的两个横截面(z=0.26 m,0.56 m)上的静压径向分布图。观察图5中6种分离器静压径向分布图发现,静压在径向上由壁面往中心逐渐减少,由于中心处气流高速旋转,中心区域形成了半径很小的负压区柱。从图5还可看出,沿着径向方向上压力梯度最大。单入口结构的分离器内静压分布出现了摆动现象,ZD型摆动幅度最小,XD-L型摆动幅度最大。静压分布的不均衡会导致分离器内气体流动不均匀,出现气体撞击壁面现象,从而引发筒壁震动。而双入口结构的分离器内静压分布呈现出很好的对称性。分离器内部对称的静压分布减少了因气流扰动而损耗的能量。对比后还可以得出,XD-L型、XS-L型分离内部负压气柱要短于其他分离器,并且负压区在排尘口上游区域就消失了,避免了负压气流将灰斗内颗粒重新卷扬。在同样的入口流速下,ZD型、XD型、ZS型、XS型4种分离器内部静压径向分布很接近,XD-L型、XS-L型分离器内部静压径向分布比较接近,并且在中心区域静压分布曲线要高于前四者,而在外部区域要低于前四者。
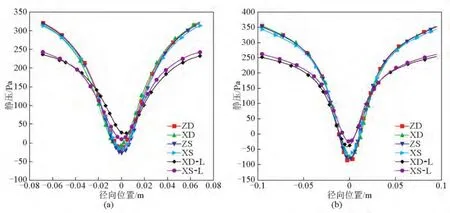
图5 不同侧向入口分离器不同截面上静压分布(从左到右为截面z=0.26 m,0.56 m)Fig.5 The contours plots for the time averaged flow variables of static pressure(from left to right:sectionz=0.26 m,0.56 m)
4.3.2 压降分析
压降又叫压力损失,引起压力损失的因素有很多[12],但主要是由于气体与旋风分离器内壁摩擦所引起的能量损失和气体因旋转而产生的能量损耗。计算不同入口流速下流场,根据计算结果绘制不同分离器各自压降、入口总压随入口流速平方的分布图以及各自压降随入口总压分布图,见图6、图7。
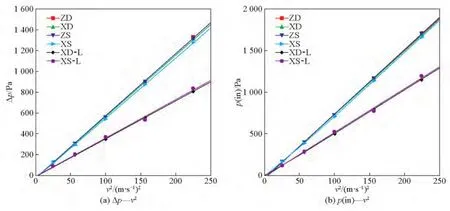
图6 6种分离器压降、入口总压与入口流速平方关系Fig.6 The relationship between the pressure drop and the inlet velocity squared as well as the inlet total pressure and the inlet velocity squared
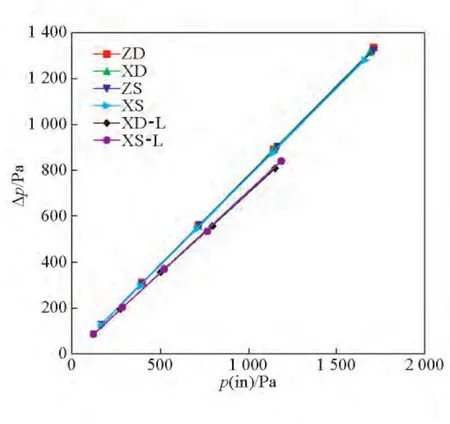
图7 6种分离器压降与入口总压关系Fig.7 The relationship between the pressure drop and the inlet total pressure
由图6a可知,在相同入口流速下,ZD型、ZS型、XD型、XS型4种分离器内部压降高于XD-L型和XS-L型分离器内部压降,并且随着入口流速的增大,压降的差值也变得越来越大;ZD型、ZS型、XD型、XS型4种分离器压降随速度平方分布曲线几乎重合,XD-L型和XS-L型分离器内部压降随速度平方分布曲线几乎重合,这说明仅仅改变进口结构的倾斜角度并不能有效地降低分离器内压降,而旋风分离器顶部为螺旋面结构能很好地起到减小压降作用,当入口切入形式确定时,分离器是相差180°的双入口还是单入口结构对分离器压降影响很小。观察图6b发现,入口总压与入口流速平方分布趋势和压降与入口流速平方的分布趋势相同,在同样的入口流速下顶部为螺旋面结构的分离器入口总压要小于其他4种分离器入口总压,根据N=PQ可知,其所消耗的能量也越小。
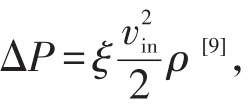
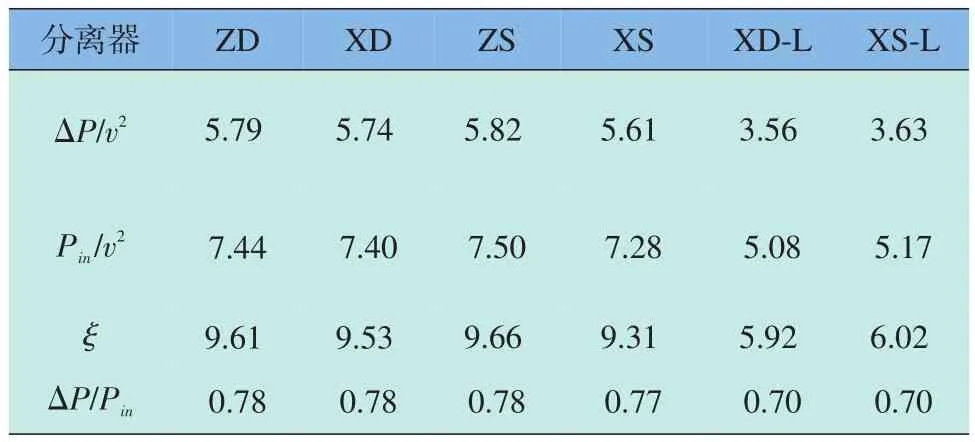
表1 旋风分离器性能参数表Table 1 Cyclone performance parameters
从图7中可以看出,旋风分离器压降与入口总压成线性关系,把压降与入口总压的比值定义为压降率,用来衡量压力损耗程度。4种旋风分离器各自压降率不随入口流速的变化而变化,为一定值。各自分离器压降率列于表1。从表1中可以得出,XD-L型、XS-L型两种分离器压降率要低于其他4种分离器,差值约为0.07。
4.3.3 速度分析
图8为6种分离器在入口流速为7.5 m/s下纵截面(Y=0)上的切向、轴向和径向速度分布云图。
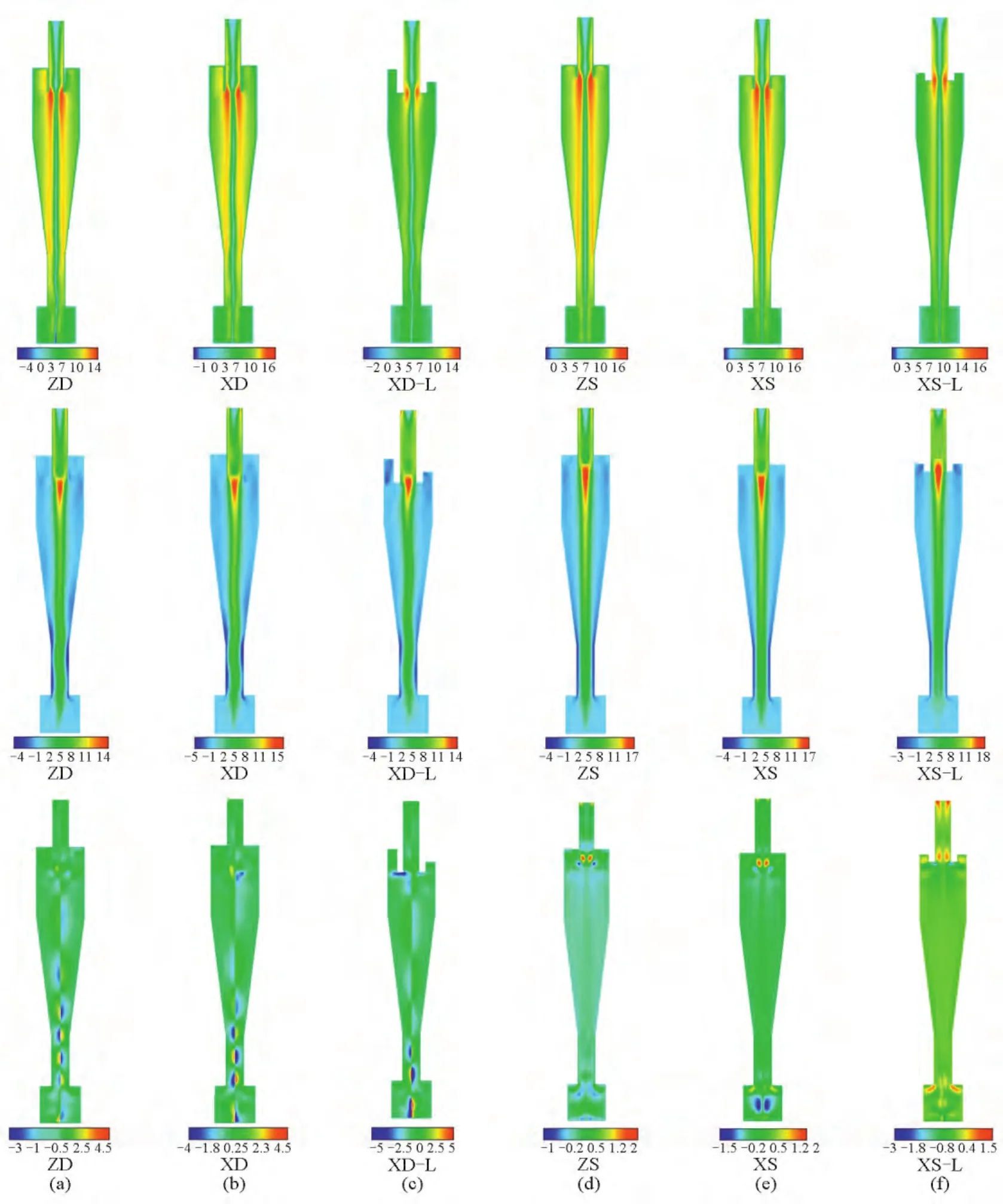
图8 从上到下为6种分离器纵截面(Y=0)切向速度、轴向速度、径向速度云图Fig.8 The contours plots for the time averaged flow variables at Y=0 from top to bottom:the tangential velocity,axial velocity and radial velocity
从图8切向速度云图可以看出在轴向上切向速度径向分布具有一致性,单入口结构分离器内切向速度分布具有摆动性,并且在排尘口下方中心轴附近出现了切向速度数值为负的现象,说明这里出现了二次涡,而二次涡容易引起颗粒返混,相反地,双入口结构分离器内切向速度径向分布呈现了很好的对称性,并且没有出现二次涡现象。从云图中也可以直观地看出切向速度最大值分布在与排气管直径相近的圆柱面上。从图8轴向速度云图可以看出壁面附近轴向速度为向下的下旋流,中心区域轴向速度为向上的上旋流,并且轴向速度最值出现在排气口下端处。下旋流能够将壁面附近的颗粒输送到灰斗内,上旋流将气体排出分离器。单入口分离器内轴向速度分布也呈现摆动现象,而双入口分离器呈现出很好的对称性。从图8径向速度云图可以看出单入口分离器在中心轴两边出现了正负对应的径向速度分布,说明气体在这些地方出现了左右摆动的流动状态,而双入口分离器呈现出较好的对称性。
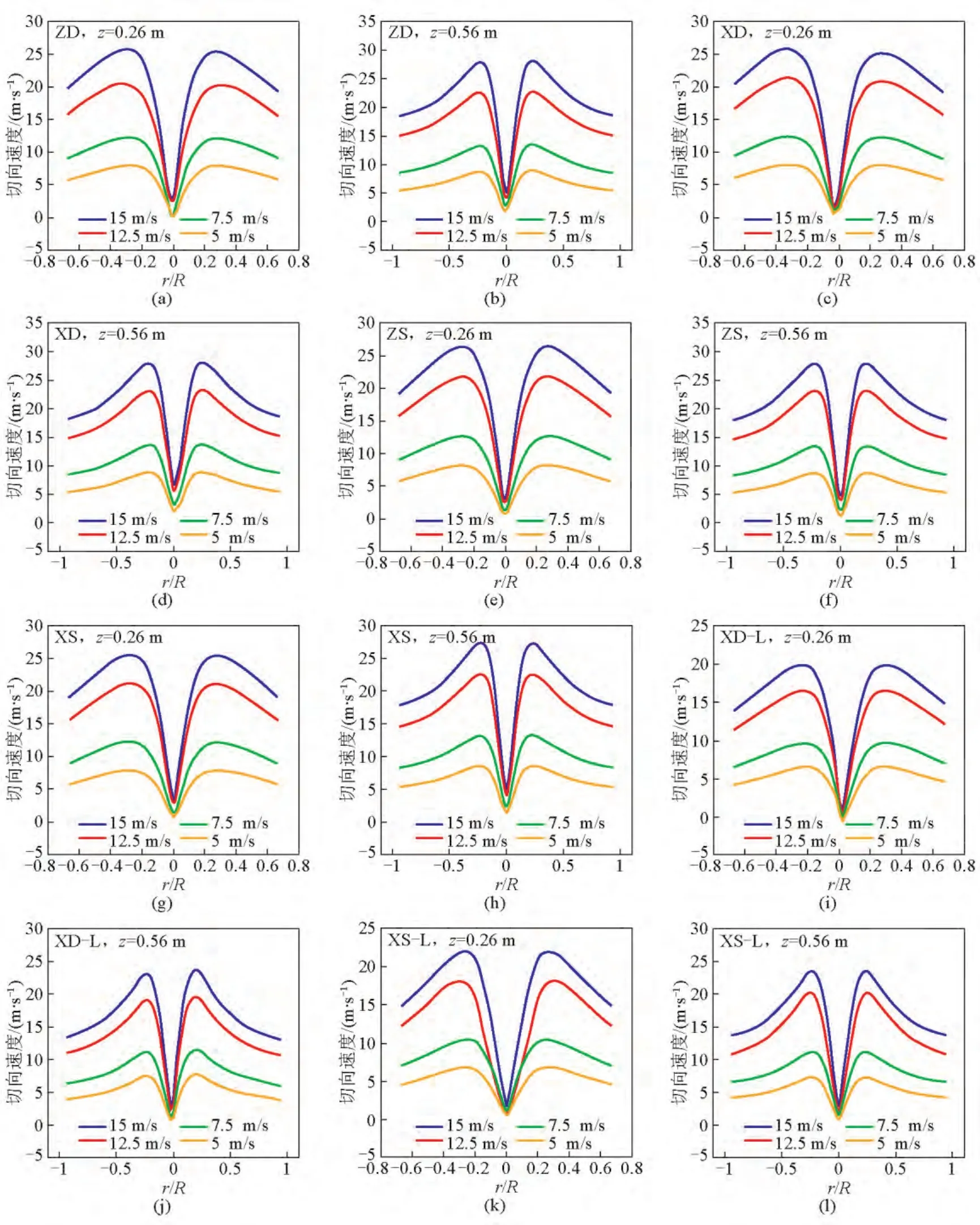
图9 6种分离器不同横截面上不同入口流速下切向速度径向分布Fig.9 The radial profile for the time averaged tangential velocity at different sections for different inlet velocity
根据之前切向速度云图分析中得到的旋风分离器内部切向速度径向分布在轴向上具有一致性的特点,图9给出了分离器直筒部分一个横截面z=0.56 m和锥形管部分一个横截面z=0.26 m上在不同入口流速下的切向速度径向分布,通过比较发现,不同分离器在相同位置的横截面上切向速度分布趋势相近。表2和表3统计了两个横截面上不同入口流速下切向速度峰值与入口流速的比值以及峰值所在的位置,由表2和表3可以发现,入口流速增加,各个分离器内横截面上峰值所在的位置几乎没有变化,直筒部分切向速度峰值所在圆柱面半径小于锥形管部分,但差值很小,并且各个分离器间横截面上峰值所在位置偏差较小。随着入口流速的增加,切向速度峰值与入口流速比值变化很小,故可用两个横截面的均值来表示分离器内流场切向速度与入口流速的比值,vZDτmax/v=1.73,vXDτmax/v=1.75 , vZSτmax/v=1.76 , vXSτmax/v=1.71 ,vXD-Lτmax/v=1.44 ,vXS-Lτmax/v=1.48 ,结合表1,可得到压降、入口总压与分离器内最大切向速度最大值平方的比值,结果列于表4。从表4中可以发现,ZD型、XD型、ZS型、XS型4种分离器压降、入口总压与切向速度峰值的比值很接近,XD-L型、XS-L型两种分离器压降、入口总压与切向速度峰值的比值很接近。结合图10和之前所论述,当6种分离器具有相同的切向速度峰值的时候,切向速度径向分布也很相近,并且后两者入口流速约是前四者入口流速的1.2倍。结合表4可得如下结论,当分离器内部具有相近的切向速度径向分布的时候,螺旋面入口结构分离器压力损失减少约25%,入口所需总压要低17%左右,处理相同气体量的能耗约减少17%。
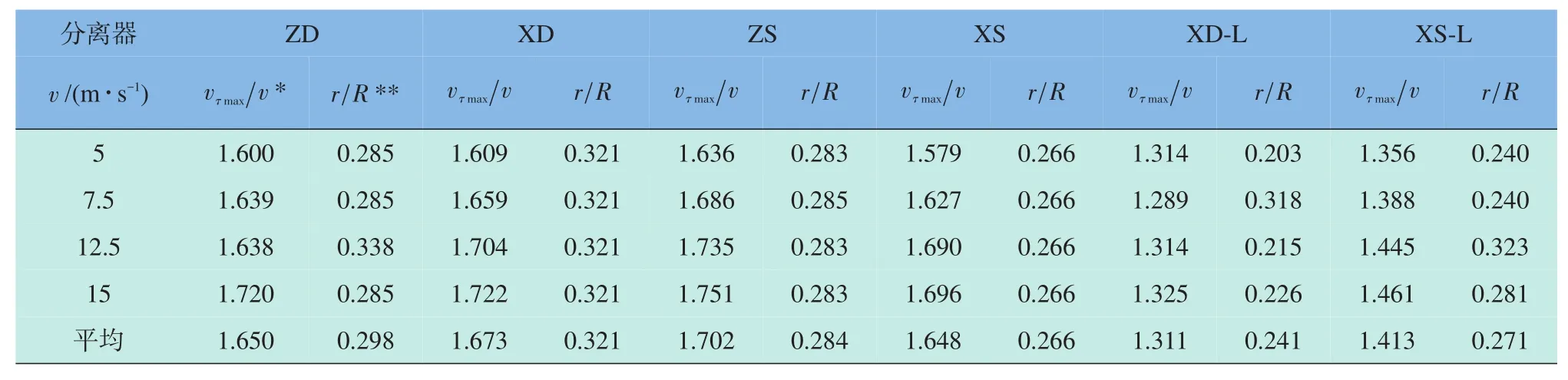
表2 横截面z=0.26 m上切向速度最大值与入口流速比值及最大切向速度位置Table 2 Comparison between the maximum tangential velocity value and ratio of inlet velocity and its position at sectionz=0.26 m
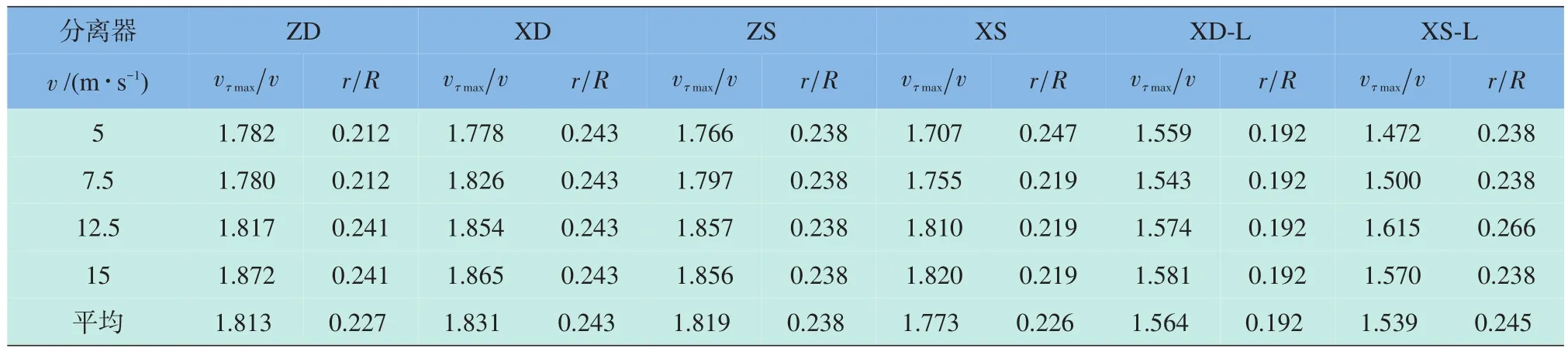
表3 横截面z=0.56 m上切向速度最大值与入口流速比值及最大切向速度位置Table 3 Comparison between the maximum tangential velocity value and ratio of inlet velocity and its position at sectionz=0.56 m

表4 分离器压降、入口总压与切向速度峰值平方比值Table 4 The ratio between the pressure drop and the maximum tangential velocity squared as well as the inlet total pressure and the maximum tangential velocity squared
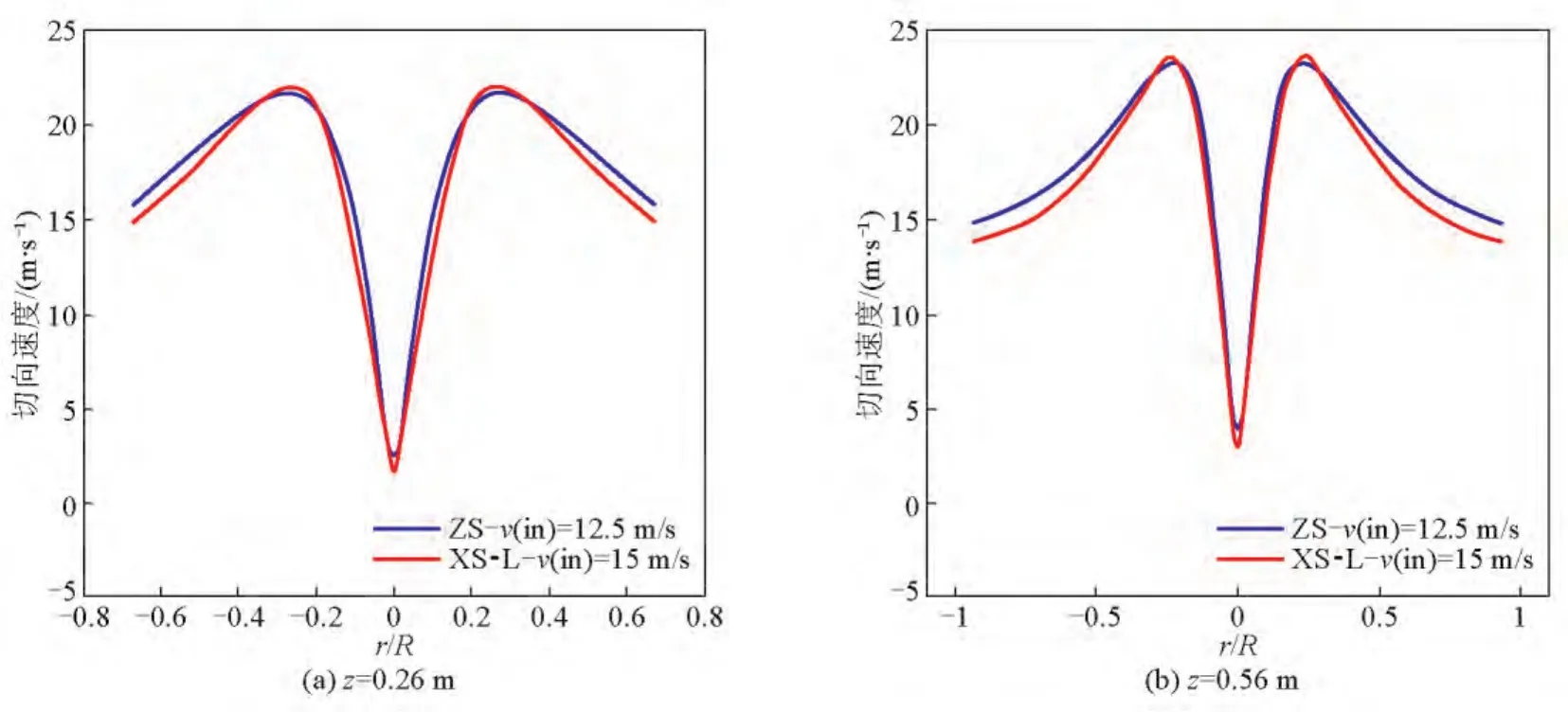
图10 具有相同切向速度峰值的切向速度径向分布Fig.10 The radial profile for the time averaged tangential velocity at different sections with same maximum tangential velocity
5 结语
1)双入口结构旋风分离器内部压力场和速度场具有更好的对称性与稳定性。
2)仅改变入口斜切角度对旋风分离器内部速度场和压力场的分布影响不大。
3)当本文中6种分离器内部具有相近的切向速度径向分布的时候,螺旋面入口结构分离器压力损失要减少约25%,入口所需总压要低17%左右,处理相同气体量的能耗要下降17%左右。
4)XS-L型分离器是一种综合性能较优的旋风分离器。
[1]王振兴,毕荣山,李玉刚,等.入口形状对旋风分离器性能的影响[J].青岛科技大学学报(自然科学版),2012,33(3):277-281.
[2]钱付平,黄星玮,纪国富.不同入口截面角旋风分离器的分离特性[J].锅炉技术,2010,41(4):14-18.
[3]吴彩金,马正飞,韩 虹.斜切双入口旋风分离器流场的数值模拟[J].煤矿机械,2010,31(9):61-63.
[4]冯喜平,赵胜海,李进贤,等.不同湍流模型对旋涡流动的数值模拟[J].航空动力学报,2011,26(6):1209-1214.
[5]张 雅,刘淑艳,王保国.使用RSM模型对旋风除尘器内湍流各向异性的数值模拟[J].工程热物理学报,2005,26(增):41-44.
[6]Mehdi Azadia,Mohsen Azadib,Ali Mohebbia.A CFD study of the effect of cyclone size on its performance parameters[J].Journal of Hazardous Materials,2010,182:835-841.
[7]张师帅.计算流体动力学及其应用[M].武汉:华中科技大学出版社,2011.
[8]赵 通,杨亚平,刘俊龙.稳态与非稳态下旋风分离器气相流场数值模拟方法研究[J].动力工程学报,2012,32(8):591-597.
[9]Khairy Elsayed,Chris Lacor.Numerical modeling of the flow field and performance in cyclones of different cone-tip diameters[J].Computers&Fluids,2011,51:48-59.
[10]Fraser S M,Abdel-Razek A M,Abdullah M Z.Computational and experimental investigations in a cyclone dust separator[J].Journal of Process Mechanical Engineering,1997,211:247.
[11]王玉梅,杨淑霞,孙国刚.旋风分离器出口边界条件对其流场模拟的影响[J].化工装备技术,2008,29(2):1-4.
[12]金国淼.除尘设备[M].北京:化学工业出版社,2002.
Numerical analysis on different lateral inlet cyclone flow field
Chen Qidong1,Zuo Zhiquan2
(1.Changshu Institute of Technology,Changshu,Jiangsu 215500,China;2.Changzhou University,Changzhou,Jiangsu 213016,China)
Numerical simulation and calculation were performed on the gas-phase flow field of the straight tangential cyclone with single entry,straight tangential cyclone with double entries,bias tangential cyclone with single entry,bias tangential cyclone with double entries,bias tangential helicoidal cyclone with single entry,bias tangential helicoidal cyclone with double entries by using RSM model.Results showed that,the pressure field and velocity field of the cyclone with double entries had better symmetry and stability;only changing the inlet angle had a limited influence on the pressure field and velocity field.When the tangential velocity distribution were similar in the six kinds of cyclone studied in this article,compared with other cyclones’,the pressure drop of the bias tangential helicoidal cyclone decreased about 25%;the inlet total pressure needed was about 17%lower;the energy consumption dropped about 17%.Moreover,bias tangential helicoidal cyclone with double entries(XS-L type)had a better energy efficiency ratio,and its performance was the most excellent.
cyclone;lateral inlet;pressure drop;inlet total pressure;energy consumption
O355;TH48
A
1009-1742(2014)02-0058-10
2013-08-29
陈启东,1962年出生,男,江苏无锡市人,教授,长期从事机械振动、流体机械的教学和研究工作;E-mail:cqd666@163.com

