水泥砂浆立方体抗压强度尺寸效应的试验研究

苏 捷，方 志

（湖南大学土木工程学院，长沙 410082）

水泥砂浆立方体抗压强度尺寸效应的试验研究

苏 捷，方 志

（湖南大学土木工程学院，长沙 410082）

通过36组强度等级分别为M30、M50和M80且边长分别为70 mm、100 mm、150 mm和200 mm的水泥砂浆立方体试件的抗压试验，研究了不同强度等级水泥砂浆试件抗压强度的尺寸效应，建立了强度等级与抗压强度尺寸效应的关系，提出了水泥砂浆抗压强度尺寸效应率的计算公式，通过试验数据验证了该公式的适用性。

水泥砂浆；尺寸效应；强度等级；立方体抗压强度

1 前言

尺寸效应是指材料的力学性能随着试件或结构几何尺寸的变化而变化[1]。大量研究结果表明，试验确定的强度不再是材料完全重复的性质，而是依赖于结构和试件几何尺寸的参数。为准确描述水泥砂浆材料的真实力学性能，对其尺寸效应进行系统研究显得尤为必要。目前国内外对混凝土材料力学性能的尺寸效应进行了一些研究[2～12]，但对水泥砂浆抗压强度尺寸效应的研究少有文献报道。此外，在对混凝土力学性能进行细观数值模拟时，通常将硬化水泥砂浆基体的力学性能假定为一常数进行分析，忽略其自身的尺寸效应，该假定的有效性尚未得到试验证实。

基于此，本文较系统地试验研究了不同强度等级水泥砂浆立方体试件抗压强度的尺寸效应，分析了强度等级对抗压强度尺寸效应的影响，得到了水泥砂浆抗压强度的临界尺寸和临界强度，建立了适用范围较广的水泥砂浆抗压强度尺寸效应率计算公式。

2 试验概况

2.1 试件模型

水泥砂浆试件的边长分别为70 mm、100 mm、150 mm和200 mm，试件尺寸如图1所示。每一尺寸的试件包含M30、M50和M80这3个强度等级，每种规格试件制作3组，立方体试件总计36组。

2.2 试验材料及配合比

各试件均采用P.O.42.5普通硅酸盐水泥，7 d和28 d抗压强度分别为38.0 MPa和58.1 MPa。所采用的硅灰的平均粒径为88nm，表观密度为2.20g/cm3，比表面积为21 m2/g。水泥和硅灰的化学成分见表1。细骨料采用细度模数为2.5的中砂，减水剂为聚羧酸系高效减水剂，减水率为25%。各强度等级水泥砂浆试件的配合比见表2。

表2 水泥砂浆配合比Table 2 The mix composition of mortar

水泥砂浆试件在成型24 h后脱模，移入标准养护室进行养护，养护温度保持在（20±1）℃，相对湿度保持为95%，试件养护龄期为28 d。每种尺寸和强度等级的水泥砂浆试件各制作3组，共计36组即108个水泥砂浆立方体试件。

2.3 试验装置及试验方法

抗压试验在YA-2000型压力试验机上进行，抗压试验装置见图2。水泥砂浆的抗压试验按照标准试验方法进行[13]。由于砂浆的抗压强度与加载速率有关[14]，全部试件均以0.3 MPa/s的速率进行加载以消除加载速率对试件抗压强度的影响。

3 试验结果

水泥砂浆立方体抗压强度如表3和图3所示，表3中试件编号采用Cx-y的形式表示，其中C表示立方体砂浆试件；x表示强度等级；y表示试件尺寸。例如，C30-100表示强度等级为M30、边长为100 mm的水泥砂浆试件。

图2 抗压试验装置Fig.2 Testing setup

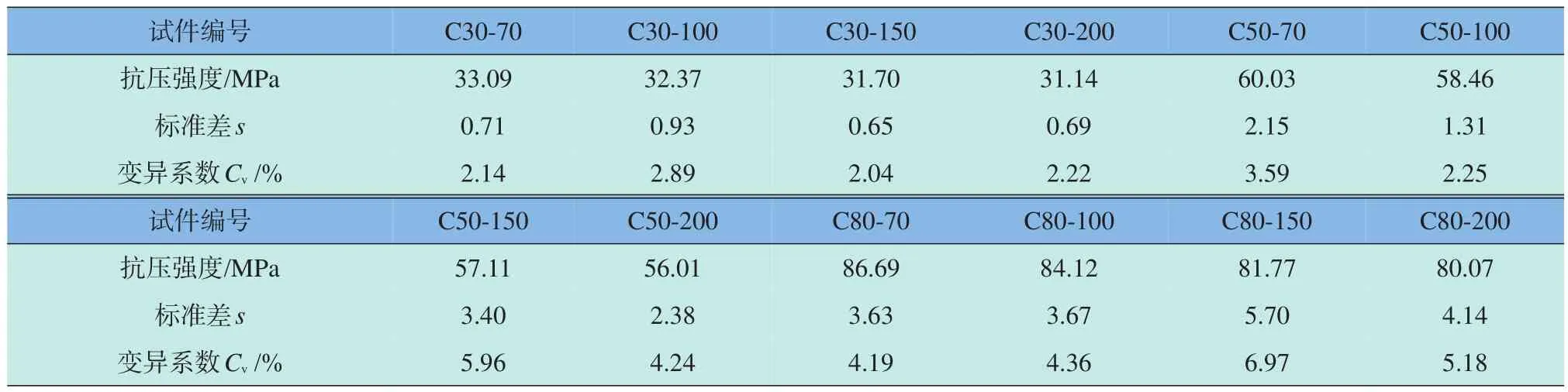
表3 水泥砂浆立方体抗压强度实测值Table 3 Mortar cubic compressive strength

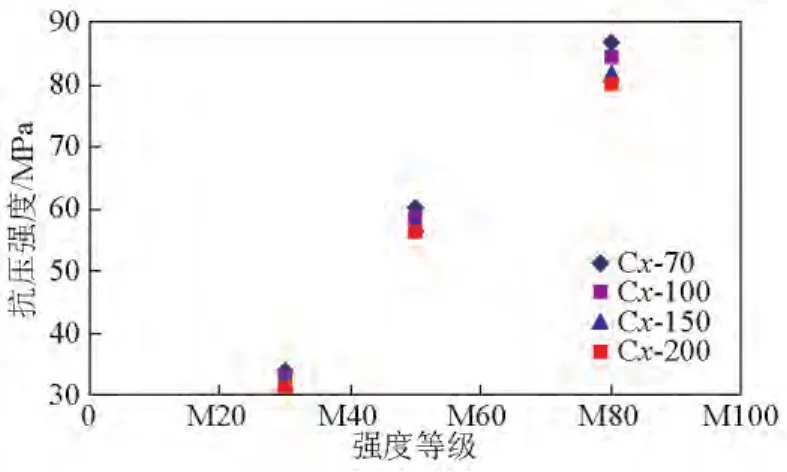
图3 水泥砂浆立方体抗压强度Fig.3 Mortar cubic compressive strength

由表3可知，各试件抗压强度的变异系数均小于7%，表明试验结果的离散性较小。从图3可以看到，各强度等级水泥砂浆试件的立方体抗压强度均随试件几何尺寸的增大而减小，抗压强度具有尺寸效应现象。

4 尺寸效应分析

4.1 抗压强度的尺寸效应

引入尺寸效应度对各试件立方体抗压强度的尺寸效应进行描述，且定义尺寸效应度γ为

式（1）～（3）中，fm,cu,70、fm,cu,100、fm,cu,150和 fm,cu,200分别表示边长为70 mm、100 mm、150 mm以及200 mm水泥砂浆立方体试件的抗压强度。

水泥砂浆立方体抗压强度尺寸效应度γ的值列于表4。图4为砂浆抗压强度尺寸效应度随强度等级变化的规律。

表4 立方体抗压强度尺寸效应度γTable 4 Detail of dimensional effect parameter γ

从表4和图4可知，水泥砂浆立方体抗压强度的尺寸效应具有以下规律。

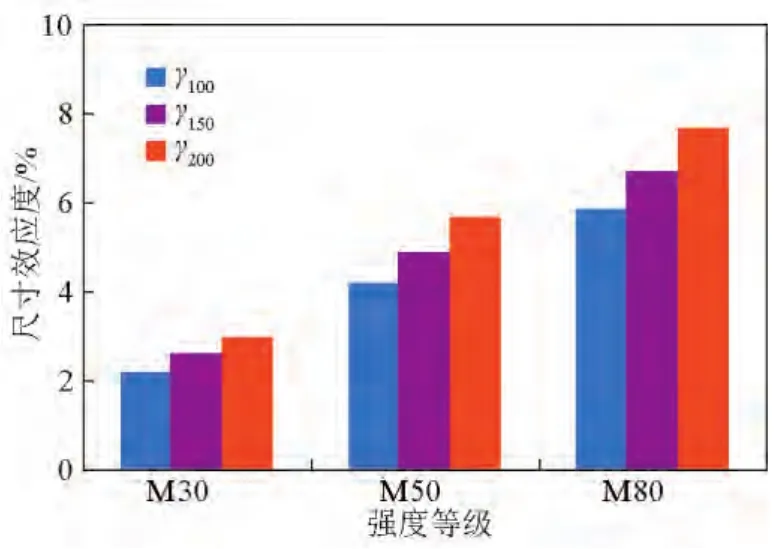
图4 不同强度等级试件的尺寸效应度γFig.4 Comparison of dimensional effect parameter γ

1）水泥砂浆立方体抗压强度具有尺寸效应现象，表现为随着试件几何尺寸的增大，相应的抗压强度逐渐减小。边长100 mm、150 mm和200 mm试件的抗压强度依次约为边长70 mm试件的98%、95%和93%。

2）水泥砂浆立方体抗压强度尺寸效应随着强度等级的提高而明显增强。强度等级为M80和M50水泥砂浆试件抗压强度的尺寸效应度分别约为强度等级M30水泥砂浆试件的2.6倍和1.9倍。造成该现象的主要原因是高强水泥砂浆试件的密实度较普通水泥砂浆更高，试件内部包含初始缺陷特别是微裂缝的数量较少，在荷载作用下，试件开裂后裂纹发展速度较快。此外，高强水泥砂浆破坏时的损伤断裂区较普通水泥砂浆更小，因此，其破坏所需的能量低于普通砂浆，导致高强水泥砂浆具有更强的尺寸效应现象。

4.2 尺寸效应率

基于能量释放准则的尺寸效应理论认为准脆性材料的尺寸效应是在达到峰值荷载前，由于一条长裂纹或一个具有微裂纹的大片断裂扩展区发生稳定的增长，特别是由于应力的重分布和由于长裂纹和大片微裂纹区的存在而引起的储存能的逐渐释放引起的[15，16]。基于能量平衡和变形协调条件，美国西北大学Bazant教授得到了试件在受压失效时的名义强度σN的尺寸效应率，如下：

式（4）中，σ∞、Db为常数，分别为尺寸极大时的名义抗压强度和结构特征尺寸；D为试件的边长。将水泥砂浆试件的抗压强度代入式（4）可得到各强度等级水泥砂浆抗压强度的尺寸效应率计算公式（5）～（7），拟合曲线见图5，M30、M50和M80水泥砂浆试件抗压强度的相关系数分别为0.932 2、0.944 6和0.920 9，这表明尺寸效应率计算公式与试验结果吻合较好，各尺寸效应率计算公式能较好地预测水泥砂浆的抗压强度。

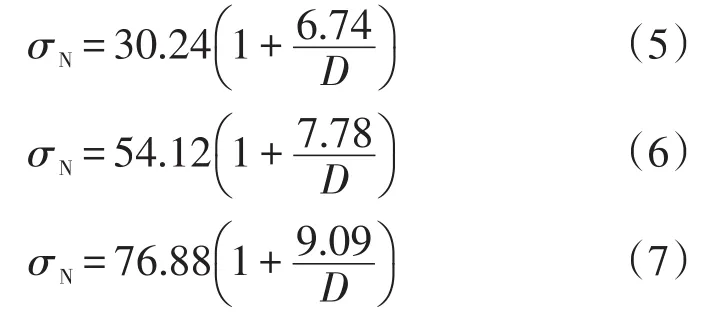
图5 尺寸效应率拟合曲线Fig.5 Fitting curves of dimensional effect rate

4.3 临界尺寸及临界强度

当试件的几何尺寸D增大时，各尺寸效应率公式计算得到的强度均有所减小，且这种减小的速率将逐渐降低。定义临界尺寸和临界强度为：当试件几何尺寸大于某一特定值Dcr时，利用尺寸效应率公式计算得到的抗压强度小于0.01，即尺寸效应率曲线上某点的切线斜率大于-0.01，则该尺寸Dcr为临界尺寸，相应的强度fcr为临界强度。从临界尺寸的定义可知，当试件的尺寸小于临界尺寸时，其强度的尺寸效应较为明显，即强度随尺寸变化的速率较大，而大于临界尺寸时，尺寸效应很小，可忽略不计。本文用尺寸效应率计算得到各试件的临界尺寸及临界强度列于表5。

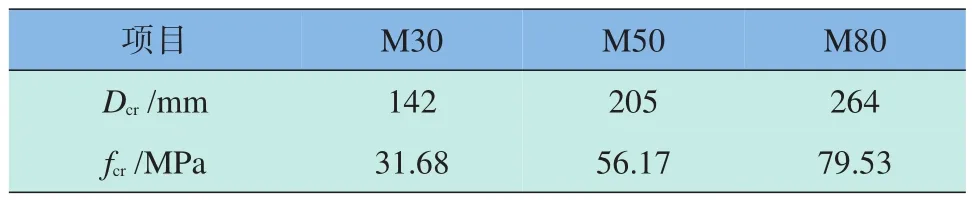
表5 砂浆立方体抗压强度的临界尺寸与临界强度Table 5 Critical dimension and critical strength of mortar cubic compressive strength

由表5可知，随着强度等级的提高，水泥砂浆抗压强度的临界尺寸逐渐增大，M80砂浆的临界尺寸分别约为M30和M50的1.9倍和1.3倍。造成该现象的主要原因是高强度等级水泥砂浆的脆性较低强度等级水泥砂浆大，尺寸效应更为显著，表现为在更大的尺寸范围内，高强砂浆的强度随其尺寸增大而明显降低。

5 结语

本文通过对不同强度等级的36组水泥砂浆立方体试件进行抗压强度尺寸效应试验研究，得到了以下结论。

1）水泥砂浆的立方体抗压强度具有尺寸效应现象，主要表现为试件尺寸较大时，其抗压强度较低，边长100 mm、150 mm和200 mm试件的抗压强度分别约为边长70 mm试件的98%、95%和93%。

2）水泥砂浆立方体抗压强度尺寸效应随着强度等级的提高而明显增强，M30水泥砂浆抗压强度的尺寸效应度约为M50砂浆的53%，M80砂浆的38%。

3）本文水泥砂浆抗压强度尺寸效应率计算公式能较好地预测抗压强度的尺寸效应。

4）随着强度等级的提高，临界尺寸有增大的趋势，M80砂浆的临界尺寸分别约为M30和M50的1.9倍和1.3倍。

[1]Bazant Z P.Size effect[J].International Journal of Solids and Structures，2000，37（4）：69-80.

[2]Su Jie，Fang Zhi，Yang Zuan.Size effect of concrete compressive strength with different reinforcement ratio[J].Key Engineering Materials，2009，400：831-835.

[3]Bazant Z P，Chen Erping.Scaling of structure failure[J].American Society of Mechanical Engineers，1997，50（10）：593-627.

[4]Neville A M.The influence of size of concrete test cubes on mean strength and standard deviation[J].Magazine of Concrete Research，1996，21（8）：31-37.

[5]Lessard M，Omar Chaallal.Testing high-strength concrete compressive strength[J].ACI Materials Journal，1993，90（4）：17-23.

[6]Elfahal M M，Krauthammer T.Dynamic size effect in normal and high-strength concrete cylinders[J].ACI Materials Journal，2005，102（2）：71-79.

[7]Malhotra V M.Are 4×8 inch concrete cylinders as 6×12 inch cylinders for quality control of concrete[J].ACI Materials Journal，1996，73（1）：14-19.

[8]李家康.高强混凝土立方体抗压强度的尺寸效应[J].建筑材料学报，2004，7（3）：81-84.

[9]钱觉时，杨再富，黄煜镔，等.高强混凝土强度尺寸效应的试验研究[J].华中科技大学学报：城市科学版，2004，21（1）：1-4.

[10]黄煜镔，钱觉时.高强及超高强混凝土的脆性与强度尺寸效应[J].工业建筑，2005，35（1）：15-17.

[11]张海燕，张子明.混凝土的统计尺寸效应[J].河海大学学报：自然科学版，2004，32（3）：291-294.

[12]朱尔玉，杨 威，王建海，等.不同形状尺寸C20混凝土试件抗压强度的关系[J].北京交通大学学报，2005，29（1）：1-4.

[13]中华人民共和国住房和城乡建设部.JGJ/T 70—2009建筑砂浆基本性能试验方法标准[S].北京：中国建筑工业出版社，2009.

[14]江见鲸，陆新征，叶列平.混凝土结构有限元分析[M].北京：清华大学出版社，2005.

[15]Bazant Z P.Size effect in blunt fracture：Concrete，rock，metal[J].Journal of Engineering Mechanics，1984，110（4）：518-535.

[16]Bazant Z P.Crack band theory for fracture of concrete[J].Materials and Structure，1983，16：155-177.

Experimental study on dimensional effect of mortar cubic compressive strength

Su Jie，Fang Zhi
（College of Civil Engineering，Hunan University，Changsha 410082，China）

The dimensional effect of mortar cubic compressive strength was investigated through compression experiments on mortar cubic specimens with the strength grade M30，M50 and M80 and specimen side length of 70 mm，100 mm，150 mm and 200 mm.The relationship between the strength grade and dimensional effect was built in this paper.Furthermore，the computational equations of dimensional effect were proposed.Finally，good agreements were found between tested data and the computational equations.

mortar；dimensional effect；strength grade；cubic compressive strength

TU317.1

A

1009-1742（2014）02-0088-05

2012-11-13

国家自然科学基金资助项目（50678063）；湖南省科技计划项目（2013CK4014）；湖南大学青年教师成长计划项目（531107040742）

苏 捷，1979年出生，男，湖南长沙市人，讲师，主要研究方向为桥梁与结构工程；E-mail：iamsujie@163.com