基于角度计算转换的瞬时相位实时生成方法

张 强 ，齐 明

（1. 航天科工防御技术研究试验中心 北京 100854；2. 中国人民解放军驻二三二厂军事代表室 北京 100086）

基于角度计算转换的瞬时相位实时生成方法

张 强1，齐 明2

（1. 航天科工防御技术研究试验中心 北京 100854；2. 中国人民解放军驻二三二厂军事代表室 北京 100086）

针对高数据率复信号的瞬时相位难以实时求解问题，提出了基于角度计算转换的求解方法。该方法先把瞬时相位的反正切运算转换成反正/余弦运算，再利用查找表代替具体的运算。证明了在角度计算转换前后，复信号I/Q两路通道噪声对瞬时相位求解结果影响的等效性。微波着陆系统(Microwave Landing System)实测数据处理结果表明，采用该方法可以在不明显降低瞬时相位求解精度的前提下，有效地降低计算量，并可完成实时处理。

复信号；瞬时相位；角度计算转换；查找表

当今通信、导航和雷达系统的发展有两个明显的特点。一方面信号的时宽带宽积逐渐增大；另一方面系统的ADC(Analog to Digital Conversion) 越来越靠近射频前端。其主要原因是，增大时宽带宽积可以有效提高通信系统的信道容量、提高导航系统的导航定位精度和提高雷达系统的作用距离及分辨率；而ADC靠近射频前端可以有效提高系统的信号处理灵活性（例如软件无线电技术[1]）。上述两个特点都会造成系统信号数据率的明显增高。以FPGA (Field Programmable Gate Array)和DSP (Digital Signal Processor)为代表的微电子技术的迅速发展在很大程度上减轻了高速数字信号实时处理的压力，但其仍难以完成一些复杂的信号处理[2]。为此，在不明显降低运算精度的前提下研究实时高效的信号处理方法在当前仍然具有很重要的意义。现有的一些通信、导航和雷达系统在对接收信号做中频数字化处理之后，往往还需要进一步求解复信号的瞬时幅度和瞬时相位[3-5]。其中瞬时相位的求解涉及到反正切运算，因而在高数据率条件下难以实时实现。这也给后续的信号处理带来很大的限制。为了克服该问题，本文提出了一种基于角度计算转换的瞬时相位获取方法。该方法先通过角度计算转换将求解瞬时相位的反正切运算转换成反正弦运算和反余弦运算，接着根据瞬时相位的求解精度需求设计相应的反正弦表和反余弦表，最后通过查找表的方式实现反正弦和反余弦运算，即通过查找表的方式实现瞬时相位的获取。具体内容请见下文。

1 瞬时相位的实时获取

若记复信号的同相分量(In-Phase)和正交分量(Quadrature-Phase)分别为xI和xQ，则其瞬时相位可定义为：

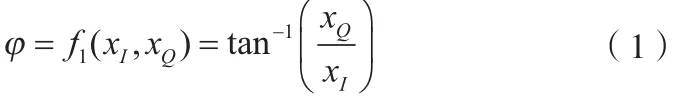
显然上式需要求解反正切函数，因此计算量较大。对于数据率很高的场合，其实时处理的压力很大。为此，下面采用简化的求解方法，具体实现步骤如下：

1 ) 角度计算的转换

为了能够利用查找表来求解瞬时相位，首先需要将式(1)的反正切函数求解变为反余弦函数求解，即：

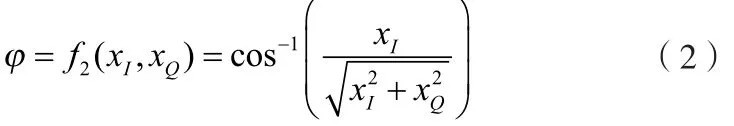
命题：在角度计算转换前后，由通道噪声和量化误差造成的瞬时相位求解误差是等效的。

证明：由式(1)得到的瞬时相位计算误差为：

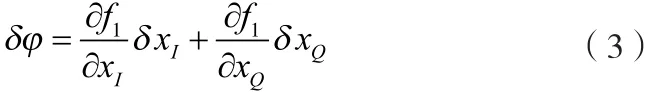
其中，δ xI和δ xQ表示由通道噪声和量化引起的 xI和xQ的测量误差。并且

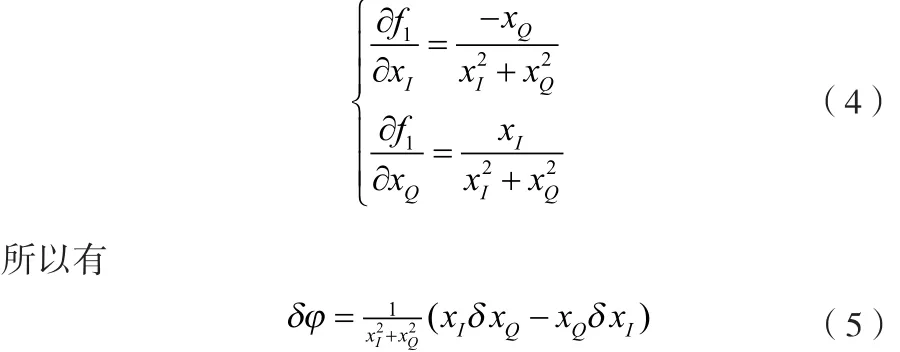
同样，由式（4）得到的瞬时相位计算误差为：

因此，上述两种角度求解方法具有相同的瞬时相位估计误差 δφ ，证毕。

同样地，也可以将反正切函数的求解变为求反正弦函数的求解。

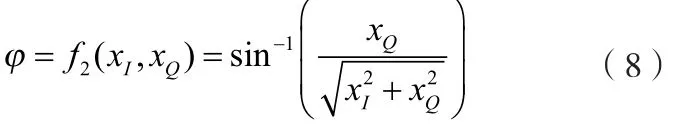
同理可以证明，上式给出的求解方法具有相同的角度求解误差，因此可以认为该角度求解方法的转换是等效的。

2 ) 缩小角度查找范围

在利用查表的方法求解瞬时相位时，缩小角度的查找范围是很有必要的，缩小查找范围意味着在相同的求解精度下，可以减小查找表的存储空间，提高查找效率。已知由IQ数据得到的瞬时相位的取值范围是00～3600，通过象限变换，其它三个象限的角度值可通过求解第一象限的角度值间接得到，所以为了缩小查表的范围，只需对求解第一个象限的瞬时相位。现设定中间变量p，使得

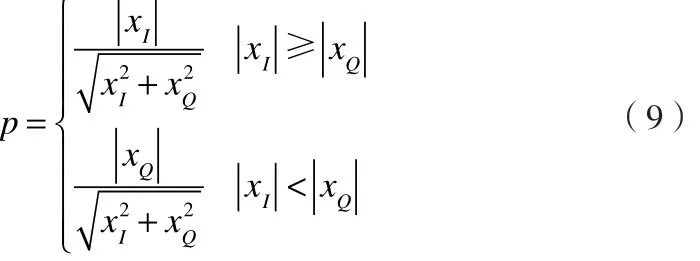
显然， 2-0.5≤p≤1。为了进一步缩小查表的范围，可采取如下的瞬时相位求解方式：

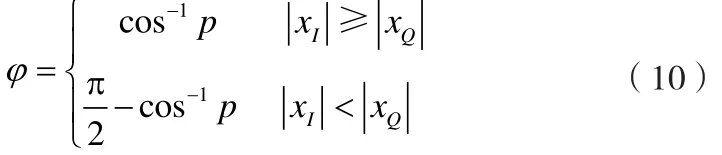
不难看出上述3种方法的估计误差是等效的。因此，第一象限的瞬时相位求解可以转换成00～450的反余弦函数求解。这样，所欲求解的角度范围便可以缩小一半。

当然，也可以采用求反正弦函数的方式实现瞬时相位的求解，先设定中间变量：

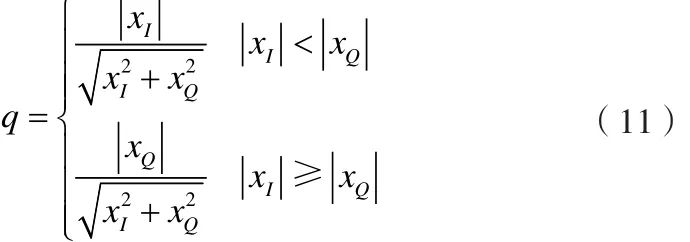
显然，0≤q≤2-0.5。由此可得到瞬时相位的求解：

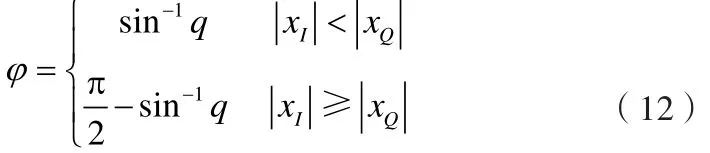
3 )查找表的实现

和正弦表和余弦表的查找方式不同，为了保证在瞬时相位的求解过程中，查找反正弦表和反余弦表所得到的角度值在整个查找范围内是均匀取值的。用于查找表的中间变量的取值就不能是均匀的，由此造成了查找反正弦表和反余弦表的困难。

首先考虑查找反余弦表的情况，用于查找表的中间变量 p的取值范围为： 2-0.5≤p≤1，让 p以0.001的步进遍历其取值范围，则总共有294个数据。因为p的均匀取值会造成 θ取值的不均匀，所以为了保证θ的精度，需要在p接近1的时候减小p取值的步进，或者是在整个遍历范围内减小p取值的步进。显然，前一种方法不利于查找，而后一种方法需要增大取值的数据点个数。为了克服查找反余弦表过程中存在的缺点，可以采用“二次查表”法作弥补，主要思想是设置反余弦表和余弦表两张查找表，首先保持p的遍历步进不变，获得了一张反余弦表，将反余弦表的内容由原来的角度值替换成下一次需要在第二张查找表中查找的起始位置和查找范围，根据该信息，中间变量p可以很方便地在接下来的余弦表中找到与自己最为接近的余弦值，该余弦值所对应的角度值即为瞬时相位的估算结果。

据此可见，由p的量化误差引起的φ值估计误差为：

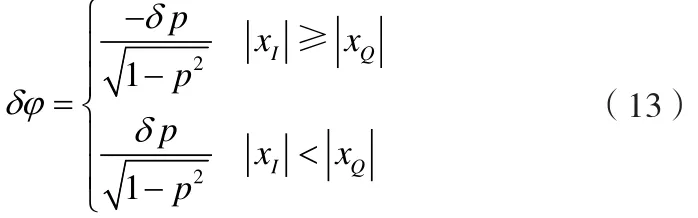
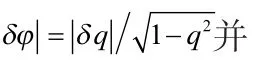
设q以步进为0.001遍历其取值范围，则反正弦查找表中共有708个数据。当q的取值接近2-0.5时，此时由量化引起的φ值估计误差最大：

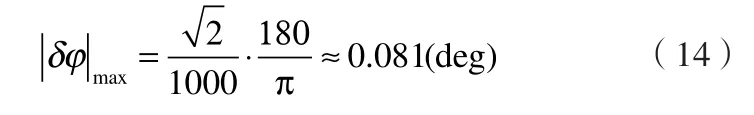
4 ) 象限恢复

求得第一象限的φ 后，将其取值扩展到4个象限：

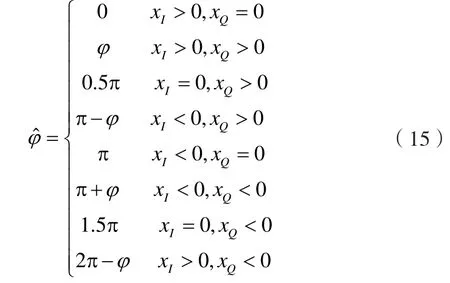
至此，有关瞬时相位的简化求解算法已经介绍完毕。总的看来，其实现步骤可以概括如下：

Step2.将所求得的瞬时幅度代入式，求得中间变量q；

Step3.根据q的取值，在00～450的反正弦表中查得φ值。因为q的查找范围是均匀量化的，所以可以很方便地实现查找；

Step4.将φ值的取值扩展到4个象限，得到所要求解的瞬时相位。

2 基于实测数据的求解精度验证

为了进一步验证本文所提方法的性能，下面结合微波着陆系统(Microwave Landing System, MLS)实测数据开展实验。

在实验中，利用MLS内场模拟器产生所需的信号（如图1所示），采用NI (National Instrument)公司的PXI (PCI eXtensions for Instrumentation)总线[6]对MLS信号进行中频数字化处理，得到的I/Q通道的信号分别如图2和图3所示。

由I/Q通道的两路信号也可以得到未经简化的瞬时相位，其结果如图4所示。本文所采用的近似求解算法的求解结果如图5所示，由近似带来的误差如图6所示。由此可见，由近似带来的误差最大不超过0.08deg，该精度是能够满足MLS机载接收机信号解调的要求。这也主要得益于本文的角度计算转换方法和查找表设计方法。

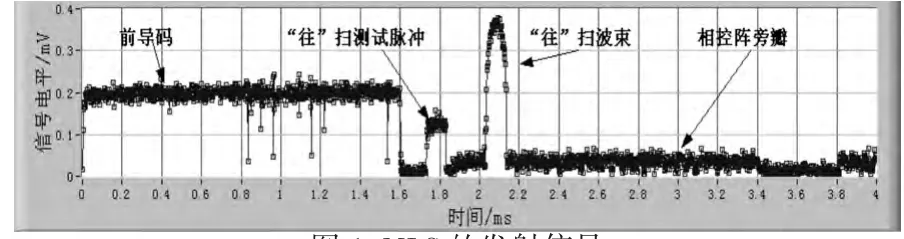
图1 MLS的发射信号Fig.1 The transmit signal of MLS

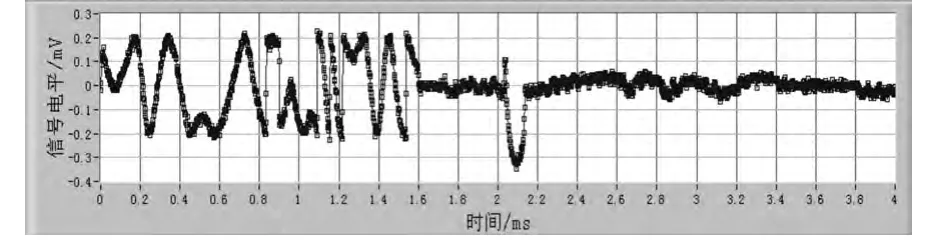
图2 MLS信号中频数字化之后的I路信号Fig.2 The in-phase component of MLS signal after intermediate frequency digitalization

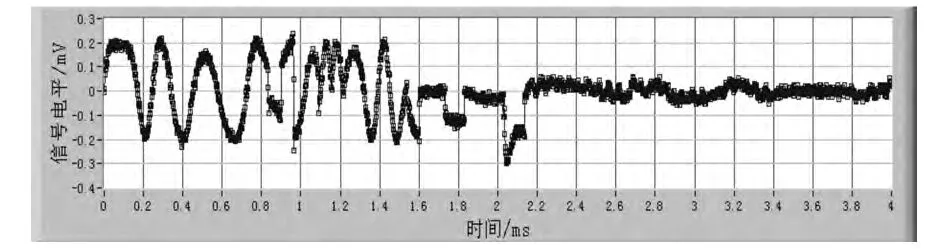
图3 MLS信号中频数字化之后的Q路信号Fig.3 The quadrature-phase component of MLS signal after intermediate frequency digitalization

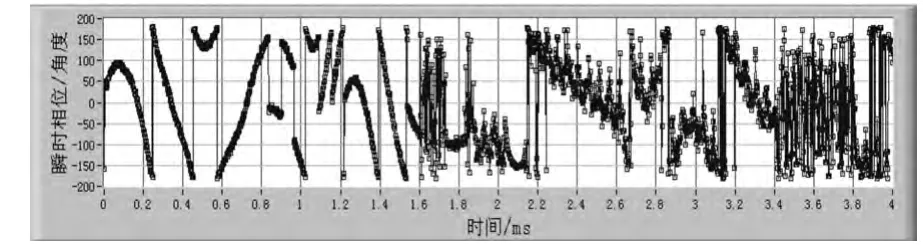
图4 MLS信号中频数字化之后的瞬时相位（未作近似）Fig.4 The instant-phase of MLS signal after intermediate frequency digitalization without any approximation

图5 瞬时相位近似求解算法的求解结果Fig.5 The instant-phase derived by the approximated calculation algorithm

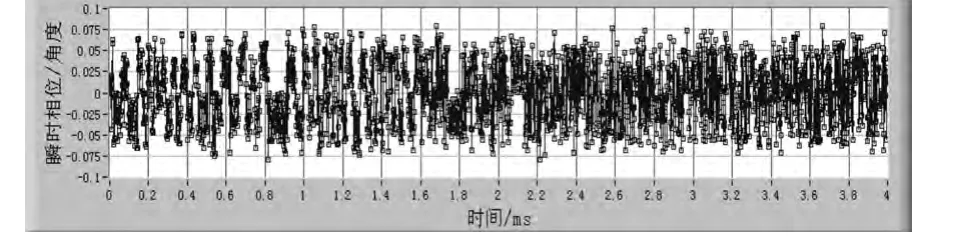
图6 简化瞬时相位算法的求解误差Fig.6 The calculation error for the simplified instant-phase calculation algorithm

3 结 论

基于角度计算转换和查找表方法的瞬时相位简化求解算法可以在近似误差的允许范围内，有效地减小计算量，因此其适合于高数据率条件下信号的实时处理。该简化求解算法也可以推广到其他的中频数字化瞬时相位求解。

[1]杨小牛，楼才义，徐建良. 软件无线电原理与应用[M]. 北京：电子工业出版社, 2002.

[2]Kumardeb B, Bivas D, Kalyan M. Novel FPGA-based LVDT signal conditioner[C] //2013 IEEE International Symposium on Industrial Electronics (ISIE),2013:1-6.

[3]Landis G P, Galysh I, Petsopoulos T. New Digital Phase Measurement System[C] //Naval Research Lab., Washington,DC. 2009.

[4]Han D,Yuanjin Zheng.A GFSK demodulator based on instant phase computation and adaptive multi-threshold quantization[C]//IEEE Asian Solid-State Circuits Conference,2009: 249-252.

[5]Vyroubal D.Optical method for instant estimate of vibration signature based on spectrum analysis of phase-modulated light pulses[J].IEEE Transactions on Instrumentation and Measurement,2004,53(1):181-185.

[6]Gutterman, Loofie. PXI for military test applications[C] // IEEE Systems Readines Technology Conference,2002:215-226.

A real-time instant phase generating method based on angle calculation transforming

ZHANG Qiang1, QI Ming2
（ 1. Aerospace Science and Industry Defense Technology Research and Test Center, Beijing 100854, China;2. PLA Military Representative Office in No.232 Factory, Beijing 100086, China）

Because of the big computational burden of arc tangent with high data rate, the real-time calculation of instant phase can be a problem for complex signal processing. To solve this problem, a new method based on angle calculation transforming is proposed in this paper. The arc tangent computation is firstly transformed to the arc sine and/or arc cosine computation, and then the look-up tables can be utilized to replace the computation of angles. The influences of I/Q channel noises on the calculation results before and after transforming are proved to be equivalent to each other. The experiment results of Microwave Landing System (MLS) are given that, with the calculation precision not degraded obviously, the method proposed can effectively reduced the computational burden of instant phase, and thus, is very suitable to real-time signal processing.

complex signals; instant phase; angle calculation transforming; look-up table

TN967.1

A

1674-6236(2014)14-0043-03

2013-09-23 稿件编号：201309165

张 强（1983—），男，安徽合肥人，硕士，工程师，技术研究员。研究方向：无线电导航检测与校验、系统可靠性设计。

book=0,ebook=429