风机叶片表面分离涡与宽频噪声辐射特性的分析

万剑峰， 杨爱玲， 戴 韧

（1.上海理工大学 能源与动力工程学院，上海200093；2.河南理工大学 机械与动力工程学院，河南焦作454000）

风机叶轮的气动噪声包括离散噪声和宽频噪声.离散噪声来自于旋转叶片周期性击打气流，它是以叶片通过频率为基频的气动噪声.宽频噪声主要来源于叶片表面的气流压力脉动.

叶片表面的气流压力脉动（声源）主要来自3个部分：来流冲击前缘的压力脉动、尾缘涡脱落形成的压力脉动［1］和叶片表面分离涡产生的压力脉动［2］.Fukano等［3］建立了叶片表面附面层尾缘涡脱落引起的升力脉动的声能量预测模型.Brooks［4］测量了3类声源形成的噪声，统计后建立了噪声预测的半经验公式.Tomimatsu等［5］和 Nakano等［6］通过实验研究了不同叶型下攻角对分离涡产生的噪声影响.居鸿宾等［7］通过实验研究了风机的气动声场，得到宽频噪声来自于紊流边界层和尾缘涡脱落，并分析了尾迹特性.Gaster［8］通过模拟和实验发现，在低雷诺数（＜106）下，叶型表面出现分离，表面压力脉动出现较大变化.

目前，对风机噪声机理的研究基本源于对实验结果的关联分析，限于实验能力，尚无能力得到流场结构与气动噪声的直接关联.采用直接模拟（DNS）来计算气动噪声（CAA）在理论上是可行的，但是限于当今计算机条件，目前还难以实现.大涡模拟（LES）具有模拟大尺度分离涡流和非定常湍流的能力，成为当前研究气动噪声机理的基本途径［9－10］.

如果计算流体力学软件（CFD）能比较准确地模拟湍流的脉动与局部分离涡流，捕捉到形成气动噪声的压力脉动源，了解每种声源（脉动源）的特性，那么仅需要气动设计即可达到很好的降噪效果.

笔者以常用的风机叶片Clark－Y叶型为模型，对叶片进行数值模拟来分析叶片表面分离涡的形成与发展规律，对比多种工况下叶片表面压力脉动的特征及其所产生的声压指向图和声压频谱图，分析叶型气动声源的远场辐射能力，为设计风机时的气动降噪提供思路.

1 流动和噪声的数值模拟

1.1 流场计算

流场和声场计算都采用Ansys V13.0软件下的Fluent.流动模拟采用基于Smagorinsky模型的大涡模拟进行计算，其控制方程表示为［11－12］

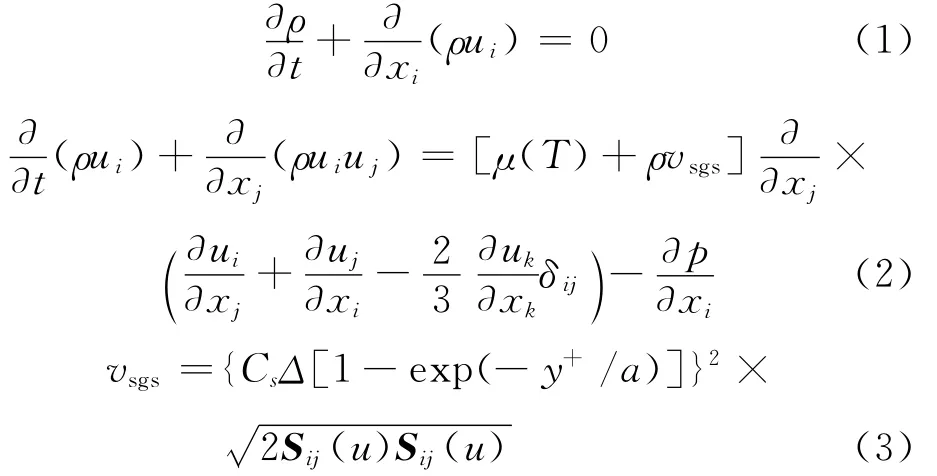
式中：ui、uj为过滤后的大尺度速度分量；μ（T）为动力黏度；l为密度；vsgs为亚格子涡黏系数；Sij为可解尺度的变形率张量；Δ为过滤尺度；Cs为模型常数，本模拟中取Cs＝1.0；δij为克罗内克符号；p 为静压；a为模型常数，a＝12.

为了加快LES的收敛速度，以定常RANS计算收敛值作为大涡模拟的初场.采用有限体积法离散方程，时间项离散采用二阶隐式格式，对流项采用二阶迎风格式，扩散项采用二阶中心差分格式，压力速度耦合迭代采用Simple算法.当数值计算的结果随时间周期性变化时，认为LES计算收敛.

1.2 声场计算

在远场线性化假设和控制面为固壁边界的条件下，由N－S方程可导出声辐射FW－H方程：

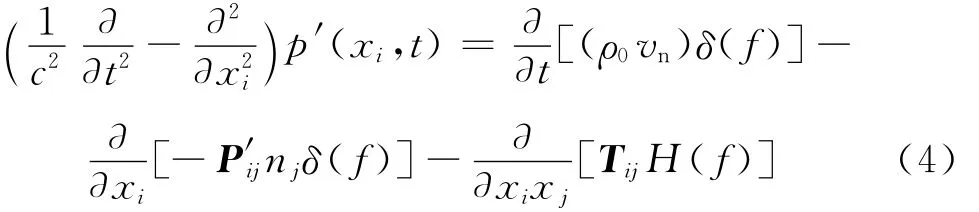
式中：c为当地声速；p′（xi，t）为观测点在t时刻的声压值；Pij为应力张量；vn为控制面法向速度；Tij为Lighthill张量；f为某一时刻的封闭控制面函数；H（f）为亥维赛德函数；下标0表示未扰动量，下标n表示在控制面外法向的方向，上标“’”表示扰动量.

式（4）等号右边为声源，依次表示单极子声源、偶极子声源和四极子声源.在低马赫数下，四极子声源噪声占总噪声的比例低，且计算繁琐，因此计算远场声压时仅需考虑单极子声源和偶极子声源［13］.

1.3 计算方法的验证

为了验证计算方法的正确性，采用二维圆柱绕流模型［14］进行测算.圆柱直径D为19mm，矩形计算区域为25D×11D，模型上游区域为5D，下游区域为19D.采用结构化分区划分网格，边界层第一层网格y＋＝1，在黏性底层内，主流区网格符合泰勒尺度［15］（λ≈（10vk／ε））.流体介质为温度27℃的不可压缩理想气体，黏度μ＝1.789 4×10－5kg／（m·s）.

模拟值与实验值的对比如表1所示.定义斯特劳哈尔数Sr＝fsD／u∞，其中fs表示涡脱落频率.由表1可知，随着流动Re的增大，Sr模拟值与实验值的误差逐步减小.考虑到风机叶片绕流的Re范围为105～106，预计模拟的误差可以控制在3%以下.

关于气动噪声方面的验证，在Re＝9×104时测量点在距圆柱圆心35D、方位角度90°（尾流为0°，逆时针为正）处，总声压级的模拟值为115.12dB，实验测量值［14］为117dB，误差为1.6%.综合流动和噪声的测量结果可知，应用大涡模拟预测气动噪声的结果是可信的.

表1 斯特劳哈尔数Sr模拟值与实验值的对比Tab.1 Comparison of Sr between simulated results and experimental data

2 计算结果与分析

2.1 计算模型

设定模型来流速度为100m／s，叶片弦长为0.06m，来流Re＝3.3×105.计算域为矩形区域，最远来流（矩形区域入口边）距前缘点8倍弦长，矩形区域出口边距尾缘16倍弦长，压力面和吸力面分别距另两条边5倍弦长.计算域外部边界设置为速度远场条件，叶型表面为无滑移边界条件.流体介质为温度27℃的不可压缩理想气体.

图1给出了气流方向、方位角以及叶片声压测点P的位置.A点为5°攻角下流动发生分离的分离点，C点为尾缘点，B点为A 点和C点之间的点，D点为5°攻角下前缘点，且A点、B点和C点在叶型的上表面，D点在叶型的下表面.

图1 声压监测点位置Fig.1 Arrangement of sound pressure measuring points

2.2 网格无关性验证

关于网格无关性验证，采用表2中的3类网格，对5°攻角下Clark－Y叶型的流动进行计算.

图2给出了稳态升力系数与尾缘点C点的瞬态压力谱图.升力系数实验值为0.9，计算值与实验值的最大误差为4.4%，说明网格对稳态结果的影响小.但是图2中，图2（a）与图2（b）差别很小且变化趋势一致，图2（c）与图2（a）和图2（b）的变化趋势一致，但细节差异明显.故网格种类1和网格种类2均可行，选取网格种类2进行计算.

表2 网格无关性验证Tab.2 Verification of grid independence

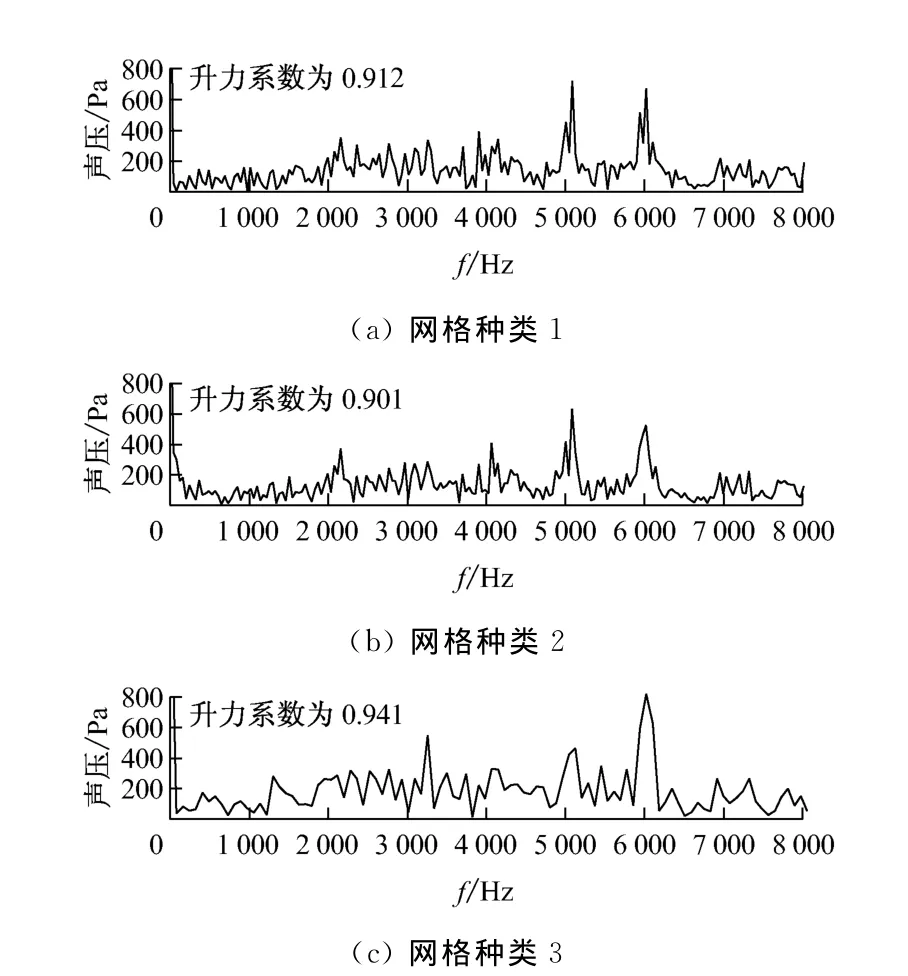
图2 网格无关性验证Fig.2 Verification of grid independence

2.3 叶片表面分离涡与压力脉动的对应

图3给出了8°攻角下，叶片吸力面的流动压力和涡量分布图，其中x，y为无量纲坐标，弦长定义为1.定义压力系数Cp为

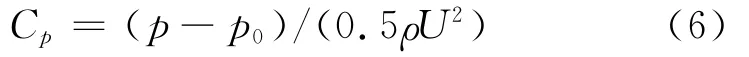
式中：p0为来流平均静压；U为来流平均速度.

在图3中，第一个压力波谷处（x＝0.18）分离点涡太小，在图中较难分辨.尾缘处，分离涡已开始远离叶片壁面，压力波谷略偏离涡心位置.其他涡量集中的地方，叶片表面都会对应地产生一个波谷.随着叶型表面各点分离涡的不断“猝发”并从叶片表面脱落进入主流区，造成叶片表面各点持续的间歇性脉动.

图4为8°攻角下流动速度流线图.由图4可知，叶片表面分离涡的流动速度要低于流体流动的速度，导致流体流动被分离涡阻碍.流体绕过分离涡时，流体速度提高，动压上升，静压下降，使得分离涡处的叶片表面压力下降.

图3 8°攻角下的吸力面压力系数和涡量分布图Fig.3 Pressure and vorticity distribution on suction surface at 8°angle of attack

图4 8°攻角下的速度分布图Fig.4 Velocity distribution at 8°angle of attack

2.4 不同攻角下的叶片表面压力脉动

叶片表面气流Cp的脉动值定义为

式中：pi，MAX和pi，MIN分别为某一Cp的极大值和极小值；K为极值个数.

图5和图6分别给出了5°攻角时，叶片吸力面和压力面的pMEAN和脉动值分布，其中pMEAN为叶片表面每点对应的Cp时均值.由图5和图6可知，吸力面压力脉动最大值处在分离点附近（x＝0.5）和叶片尾缘（x＝1），并且在分离点到尾缘之间的区域（0.5＜x＜1）都保持较大的压力脉动.对于压力面来说，尾缘（x＝1）压力脉动大小相当于吸力面尾缘（x＝1）的压力脉动，同时，在压力面的前缘点（x＝0）也有一个较小的压力脉动极值.

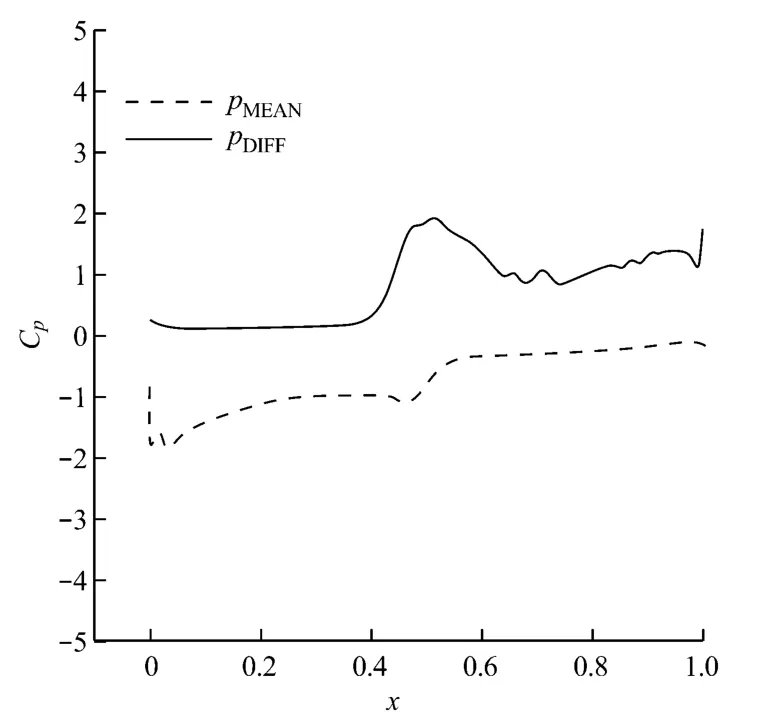
图5 5°攻角时叶片吸力面的pMEAN和脉动值分布Fig.5 Profiles on blade suction surface at 5°angle of attack

图6 5°攻角时叶片压力面的pMEAN和脉动值分布Fig.6 Profiles on blade pressure surface at 5°angle of attack

图7 8°攻角时叶片吸力面的pMEAN和脉动值分布Fig.7 Profiles on blade suction surface at 8°angle of attack

图7和图8给出了8°攻角时，叶片吸力面和压力面的pMEAN和脉动值分布.由图7和图8可知，在分离点附近和尾缘处压力脉动极大，在它们之间的

区域压力脉动较大，前缘点的压力脉动极值比5°攻角时更大.

由以上模拟结果可以看出，叶型表面的压力脉动（声源）主要有3个：（1）前缘点的压力脉动；（2）尾缘区的压力脉动；（3）分离涡在吸力面产生的压力脉动.从脉动幅值判断，前2个的脉动强度相当，而第3个的脉动强度最低.

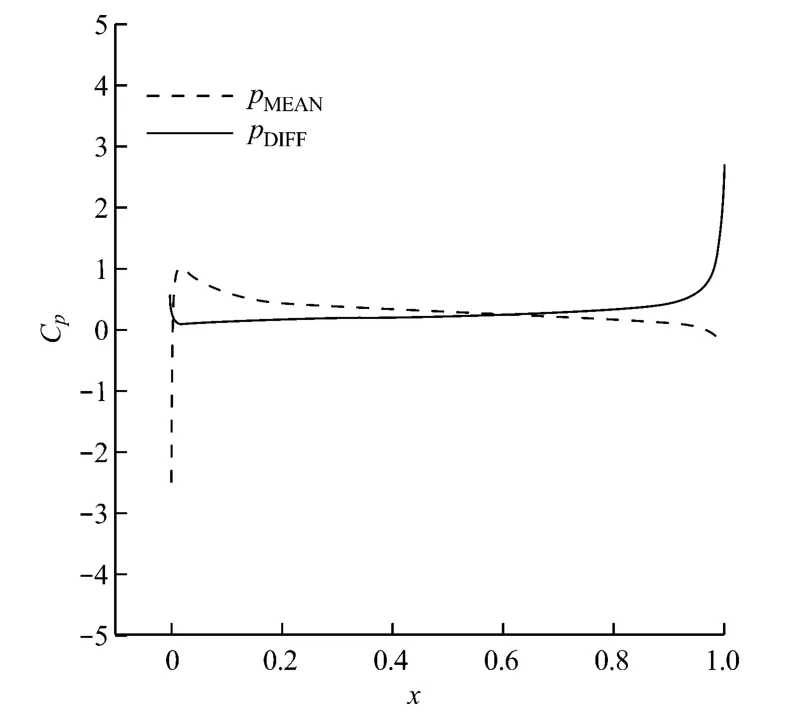
图8 8°攻角时叶片压力面的pMEAN和脉动值分布Fig.8 Profiles on blade pressure surface at 8°angle of attack

2.5 特征点压力频域分析

图9给出了5°攻角时叶片表面3个点的压力脉动频谱域分布图.从图9可以看出，A点和B点在6 500Hz以上频率时压力仍有较大值（见图9细线框），但C点却没有，故此特征由分离涡产生.其他两处尖峰5 080Hz和6 100Hz（见图9小圆圈），A点和B点来源于分离涡，C点来源于尾缘涡脱落，是共有特征.

图9 A点、B点和C点的压力脉动频域分布Fig.9 Pressure spectrums at points A，Band C

图10给出了5°攻角时D点的压力脉动频域分布图.从图10可以看出，D点出现240Hz的尖峰（见图10小圆圈），但吸力面的点（A点，B点和C点）却没有，故240Hz的尖峰是前缘点的特征.

图10 D点的压力脉动频域分布Fig.1 0 Pressure spectrums at point D

图11给出了5°攻角时吸力面和压力面分别对P点的声压频域分布图.由图11可知，压力面声压频域分布有前缘点特征，注意到前缘点的压力脉动要远小于其他区域，可知前缘点的声辐射能力最强；吸力面声压频域分布图仅有共有特征并无分离涡特征，故共有特征能产生较强的辐射；分离涡在6 500 Hz以上频率的辐射能力低.

图11 吸力面与压力面的声压频域分布（0.8m，270°）Fig.1 1 Spectrums of sound pressure on both suction and pressure surface（0.8m，270°）

2.6 表面声源的辐射分析

图12给出了在5°攻角、5 080Hz频率下，在r／c＝13（r为接收点到叶片中心距离，c为弦长）处观察到的声压指向图.对比图12的2个表面声源声压指向图，二者均有90°指向，不同的是压力面还有140°和220°指向.对比两表面的压力脉动，二者均有尾缘的涡脱落压力脉动，不同的是吸力面有分离涡脉动，压力面有前缘脉动.相同部分脉动产生了90°指向，不同部分前缘脉动产生了140°和220°指向，另外分离涡脉动却没有产生明显特征.故分离涡的共有特征为声辐射能力低于前缘和尾缘压力脉动的声辐射能力.

综上所述，前缘点压力脉动非常集中，几乎是一个前缘壁面上的点声源.尾缘区压力脉动都是源于同一涡脱落，各点压力脉动相位差小.分离涡产生的压力脉动虽大，但各点相位都不同.因此，前缘点压力脉动声辐射能力最强，而相位差小、分布区域小的尾缘压力脉动声辐射能力次之，分布区域大、各点相位差大的分离涡产生的压力脉动声辐射能力最低.

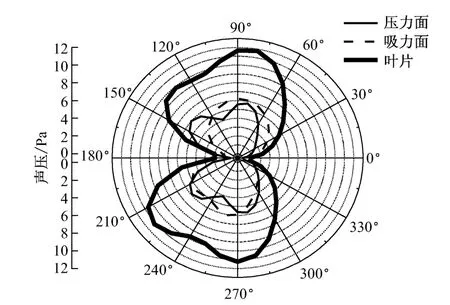
图12 13倍弦长处的声压指向图Fig.1 2 Sound pressure direction diagram at 13times the chord length

3 结 论

（1）在小攻角叶型发生分离时，分离涡沿叶片表面形成涡束，在分离涡与叶片表面的接触处形成表面压力低谷，这些表面压力脉动形成了流动宽频噪声的一个新声源.

（2）叶片宽频噪声的3个来源中，前缘点的压力脉动声辐射能力最强，尾缘区压力脉动声辐射能力次之，叶片表面的涡流产生的压力脉动最大，但其声辐射能力最低.宽频噪声主要来源于前缘点压力脉动和尾缘区压力脉动，控制前缘噪声与尾缘边界层脱落噪声，对风机的降噪设计更有意义.

［1］YANG Zhiyin，VOKE P R.Large－eddy simulation of boundary－layer separation and transition at a change of surface curvature［J］.Journal of Fluid Mechanics，2001，439：305－333.

［2］LIN J C M，PAULEY L L.Low－reynolds－number separation on an airfoil［J］.AIAA Journal，1996，34（8）：1570－1577.

［3］FUKANO T，KODAMA Y，SENOO Y.Noise generated by low pressure axial flow fans，I：modeling of the turbulent noise［J］.Journal of Sound and Vibration，1977，50（1）：63－74.

［4］BROOKS T F，POPE D S，MARCOLINI M A.Airfoil self－noise prediction［M］.Washington DC，USA：NASA，1989：36－45.

［5］TOMIMATSU S，FUJISAWA N.Measurement of aerodynamic noise and unsteady flow field around a symmetrical airfoil［J］.Journal of Visualization，2002，5（4）：381－388.

［6］NAKANO T，FUJISAWA N，OGUMA Y，et al.Experimental study on flow and noise characteristics of NACA0018airfoil［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95（7）：511－531.

［7］居鸿宾，钟芳源.风机气动声场及其相似性实验研究［J］.流体机械，1995，23（7）：3－6.JU Hongbin，ZHONG Fangyuan.Experiment study on fans＇aerodynamic sound field and its similarity［J］.Fluid Machinery，1995，23（7）：3－6.

［8］GASTER M.The structure and behavior of laminar separation bubble［M］.London，UK：AGARD CP－4，1969.

［9］傅慧萍，缪国平.大涡模拟在噪声计算中的应用［J］.上海交通大学学报，2009，43（8）：1307－1311.FU Huiping，MIAO Guoping.Application of LES method to flow noise calculation［J］.Journal of Shanghai Jiaotong University，2009，43（8）：1307－1311.

［10］卓文涛，季锃钏，陈二云，等.翼型气动性能与噪声的综合优化设计方法［J］.动力工程学报，2012，32（6）：481－486.ZHUO Wentao，JI Zengchuan，CHEN Eryun，et al.Comprehensive optimization on aerodynamic and aeroacoustic performance of airfoils［J］.Journal of Chinese Society of Power Engineering，2012，32（6）：481－486.

［11］LARCHEVÊQUE L，SAGAUT P，MARY I，et al.Large－eddy simulation of a compressible flow past a deep cavity［J］.Physics of Fluids，2003，15（1）：193－211.

［12］LENORMAND E，SAGAUT P，COMTE P，et al.Subgrid－scale models for large－eddy simulations of compressible wall bounded flows［J］.AIAA Journal，2000，38（8）：1340－1350.

［13］CURLE N.The influence of solid boundaries upon aerodynamic sound［J］.Proceedings of the Royal Society，1955，231（1187）：505－514.

［14］REVELL J D，PRYZD R A，HAYS P A.Experimental study of airframe noise vs.drag relationship for circular cylinders［R］.Washington DC，USA：NASA，1977：120－122.

［15］张兆顺，崔桂香，许晓阳.湍流大涡数值模拟的理论和应用［M］.北京：清华大学出版社，2008：118.