声矢量阵快速子空间方位估计算法

梁国龙，张 柯，安少军，范 展

(1.哈尔滨工程大学水声技术重点实验室，150001哈尔滨;2.哈尔滨工程大学水声工程学院，150001哈尔滨)

声矢量传感器由声压传感器与轴向正交的振速传感器组成，可同时、共点测量声场的声压和质点振速信息，与传统的声压传感器相比，其获得的信息量大为增加.近十年来，许多文献对声矢量阵的高分辨DOA算法进行了广泛研究［1-5］.在文献［1］中，基于Nehorai处理框架的声矢量阵信号处理方法，仅仅把振速信息看成与声压相同的独立信息来处理，并没有利用声矢量阵中声压和振速的相干性，即抗各向同性噪声的能力.基于声压振速联合处理的抗干扰能力，文献［2-5］提出了一系列基于传统子空间算法(诸如MUSIC、ESPRIT等)的声压与振速联合处理的声矢量阵高分辨DOA估计方法，与Nehorai框架的算法相比，其在多目标方位估计精度、分辨信噪比门限、分辨成功概率等方面都具有更好的性能，但是，以上算法在提高声矢量阵DOA估计性能的同时，其繁重的计算量却没有得到改善，这使得工程应用受到限制.

在众多的子空间快速估计算法中，多级维纳滤波器(MSWF)［6-12］因无需估计协方差矩阵从而使其可以应用在小样本支撑的信号环境中，而且收敛速度快，能够对时变信号进行快速跟踪，更重要的是其无需特征值分解运算，大大降低了运算量.文献［6］将多级维纳滤波器应用到标量阵的子空间分解中，指出若取多级维纳滤波器的期望信号为参考阵元的接收信号，则经前向递推得到的多级维纳滤波器的匹配滤波器可作为信号子空间基的估计值.文献［7］将参考阵元的输出延时后作为多级维纳滤波器的期望信号，在空时白噪声条件下，提高了文献［6］算法的DOA估计性能，但是其期望信号选择方式影响了MSWF算法的实时性，且当噪声具有时间相关性时，该算法性能将与文献［6］算法相同.文献［8-9］在硬件平台上实现了MSWF算法对信号子空间的快速估计，并取得了良好的效果.文献［10］将多级维纳滤波器应用到MMUSIC(Modified MUSIC)算法中，实现了基于Nehorai框架的声矢量阵相干源的快速DOA估计.基于声压振速联合处理的抗各向同性干扰特性，本文提出一种新的期望信号选择方法，不影响MSWF算法的实时性，且使MSWF算法在保持高精度DOA估计的同时，大大减小了计算量.

1 矢量阵声压振速组合MUSIC算法

1.1 声矢量阵输出模型

考虑二维平面情况下，M个矢量传感器等间距排列成一声矢量阵线阵，假设均为各向同性阵元，放置于各向同性的均匀流体介质中，阵列远场中在以线阵轴线的法线为参考的θk(k=1，2，…，K)处有K个波长为λ的窄带平面波入射，则声矢量阵的输出模型为

式中:Yp(t)为声压传感器的输出矢量;Yvx(t)为x方向振速传感器的输出矢量;Yvy(t)为y方向振速传感器的输出矢量;A(θ)=［a(θ1)，a(θ2)，…，a(θK)］为声矢量阵中M维声压阵的阵列流形矢量．其中，a(θk)=［1，e-jβk，…，e-j(M-1)βk］T为第k个信源的 导 向 矢 量;βk=2πdsin(θk)/λ;S(t)=［s1(t)，s2(t)，…，sK(t)］T为阵列接收的信号矢量;Np(t)为声压传感器接收到的零均值高斯白噪声，Nvx(t)为x方向振速传感器接收到的零均值高斯白噪声，Nvy(t)为y方向振速传感器接收到的零均值高斯白噪声，各个方向接收到的噪声相互独立;Φvx为x方向振速传感器输出的系数矩阵;Φvy为y方向振速传感器输出的系数矩阵，它们可表示为

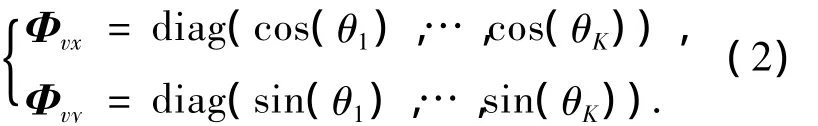
1.2 声压振速联合处理的测向方法

文献［2］对矢量阵两轴向的振速输出进行组合，可得到振速在某个参考方向θr上的电子旋转矢量

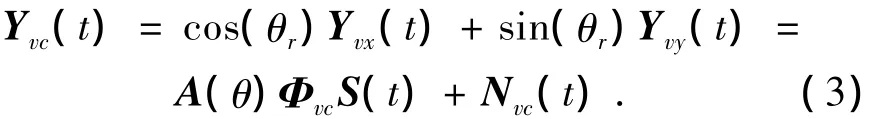
其中

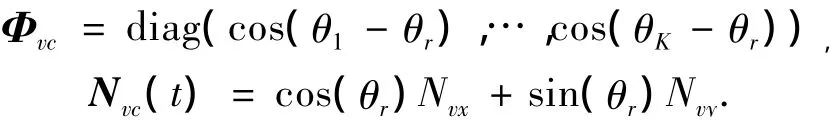
定义声压振速联合信息处理的声矢量阵P-V协方差矩阵为

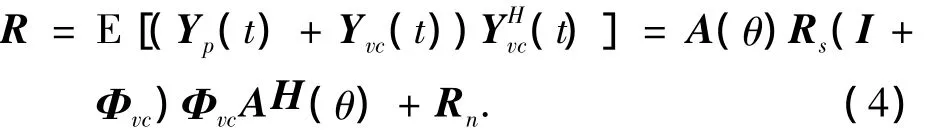
式中:Rs=E［(S(t)SH(t))］，Rn为噪声的协方差矩阵，Ⅰ为单位阵．

对R进行特征值分解并将其特征向量按照特征值的大小降序排列可得

式中Un为矢量阵列噪声子空间．则声矢量阵声压振速组合MUSIC算法的空间谱为

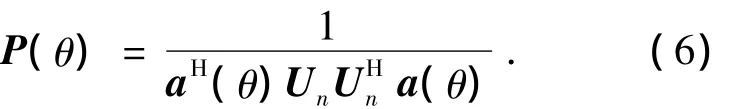
上述算法既进行了声矢量阵声压振速联合信息处理，又利用了矢量阵组合(P+Vc)Vc的指向性增益，因此获得了较高的DOA估计性能.然而，由于R不在具有Toeplitz结构，需通过一定的方法［3］对其进行Toeplitz重构.

2 声矢量阵快速子空间估计算法

2.1 MSWF算法求解信号子空间

文献［6］指出，多级维纳滤波器是一种有效的降维滤波技术，其在最小均方误差意义下可得到维纳霍夫方程的渐近最优解而无需协方差矩阵的求逆运算.对于标量阵，其协方差矩阵为

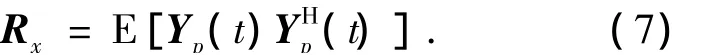
而Wiener-Hoof方程RxWwf=rxd的渐进最优解为

基于相关相减的MSWF是一种有效的多级维纳滤波结构，其迭代过程如下:

步骤1 初始化d0(t)和x0(t)，

步骤2 前向递推:令i=1，2，…，M;hi=Edi(k)==xi-1(t)-hidi(t)．

步骤3 后向递推:eM(t)=dM(t)，

令i=M，M-1，…，1;

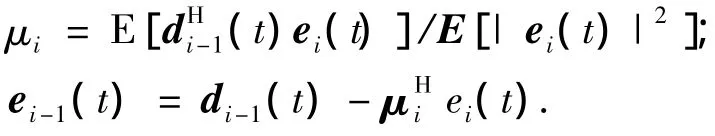
式中d0(t)为 MSWF算法中的期望信号.文献［6］指出，当入射信号波形未知时，期望信号可取为参考阵元的输出.令则MSWF的递推过程等价于在Krylov子空间κ(M)(Rx，rxd)求解 Wiener Hopf方程［13］，经M级递推得到的各级滤波器的匹配滤波器h1，h2，…，hM构成了M维Krylov子空间κ(M)(Rx，rxd)的一组基．文献［7］指出，若rxd可表示为信号子空间对应的所有特征向量的线性组合，则K维Krylo

v子空间κ(M)(Rx，rxd)等价于信号子空间．

2.2 新算法的原理与实现

基于声压振速联合信息处理，取声矢量阵互协方差矩阵为

给出期望信号d0(t)一种新的取法

定理 当期望信号d0(t)取为声矢量阵的电子旋转矢量时，rxd可以表示为信号子空间对应的所有特征向量的线性组合．

证明 期望信号和观测数据的互相关函数为

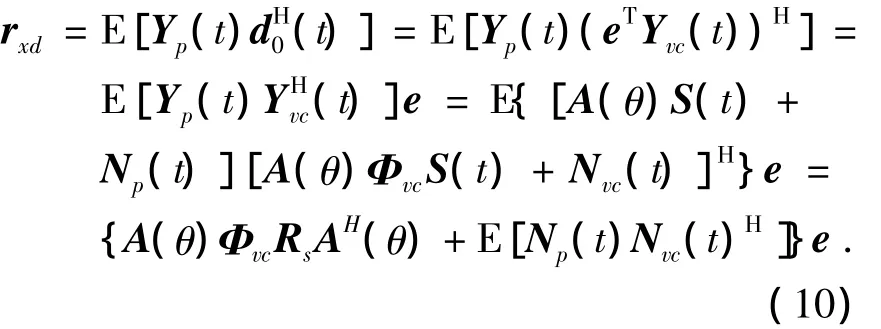
令R's=ΦvcRs，则有

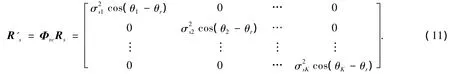
式中:R's为对角矩阵为入射信号功率．

由于声矢量阵声压传感器与振速传感器接收到的噪声互不相关，可得

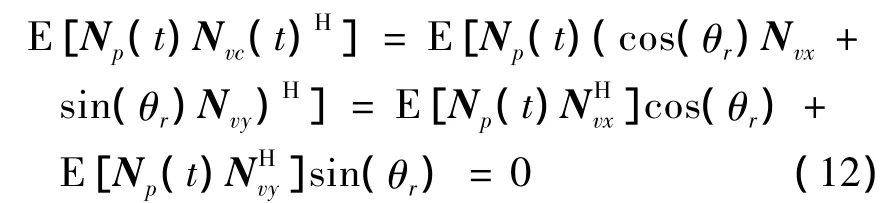
将式(12)代入式(10)得

由上式可以看出，rxd为所有信号特征向量的线性组合，命题成立.

上述定理表明，当取参考信号d0(t)=eTYvc(t)时，Krylov子空间 κ(K)(Rpv，rxd)等价于信号子空间．则经K级递推得到的各级滤波器的匹配滤波器h1，h2，…，hK即为K维Krylov子空间κ(K)(Rpv，rxd)的标准基，运用MSWF快速子空间估计算法获得声矢量阵入射信号的子空间．声矢量阵快速子空间方位估计算法的具体步骤如下:

步骤1 由式(3)得到参考方向θr上的电子旋转矢量Yvc(t)．

步骤 2 取d0(t)=eTYvc(t)，x0(t)=Yp(t)．

步骤3 令i=1，2，…，K;hi=(t)］/

上式得到的各级滤波器系数H=［h1，h2，…，hK］张成信号子空间．

步骤4 由下式可得到声矢量阵的空间谱估计为

2.3 算法性能分析

与文献［2］相比本文的主要区别在于获取噪声子空间不同，文献［2］算法通过计算阵列的协方差矩阵并对其进行特征值分解来获取噪声子空间，需要的计算量为O(M2N+4M3/3)，而本文算法是通过MSWF递推来获得噪声子空间，所需计算量仅为O(KMN)，实际应用中，入射信源数K远远小于阵元数M，故本文算法的计算量远小于文献［2］算法．另外，由式(10)～(13)可以看出，本文提出的算法有效地抑制了各向同性噪声，充分利用了声压振速信息联合处理的良好抗噪能力，提高了声矢量阵的处理增益．式(13)中，当存在cos(θk-θr)≤0的入射信号时，R's将分别变为非满秩矩阵和不定阵，文献［3］进行了深入的讨论．

3 仿真与分析

3.1 计算量比较

假设2个信源入射到阵列，图1(a)表示快拍数N=200时，文献［2］算法与本文算法的计算量随阵元数的变化曲线，随着阵元数的增加，本文算法的计算量数值在一条斜率很小的直线上，计算量增加并不明显，而文献［2］算法的计算量呈指数增长趋势，阵元越多，计算量增加越明显.在图1(b)中，阵元数M=16，文献［2］算法与本文算法的计算量随快拍数的增加呈直线增长趋势，与文献［2］算法相比，代表本文算法计算量直线的斜率很小，这说明随着快拍数的增加，文献［2］算法计算量的增幅远大于本文算法.

图1 计算量对比

3.2 空间谱估计性能比较

假设16个声矢量传感器沿x轴以d=λ/2等间距布放，其中λ为入射信号源在水中的波长，3个互不相关的等功率高斯窄带信号分别从10°，15°和40°方向入射，快拍数为1 000.

图2为不同信噪比时，文献［2，6］算法及本文算法的空间谱估计，从图2(a)中可以看出，当信噪比为15 dB时，3种算法均能准确分辨出3个入射信号的方位，其中文献［6］算法的“谱峰”较钝，本文算法与文献［2］算法的“谱峰”较尖锐，这表明高信噪比条件下，本文算法与文献［2］算法的分辨性能相近，而文献［6］算法的分辨性能较差;图2(b)中，信噪比为5 dB，本文算法的“谱峰”略钝于文献［2］算法，但都能准确分辨角度相近的2个入射信号，而文献［6］算法却未能成功分辨出入射角为10°的信号，这表明信噪比较低时，本文算法的分辨性能稍逊于文献［2］算法，却能够分辨入射角度相近的信源，而文献［6］算法的分辨性能严重下降，不能分辨入射角度相近的信源.

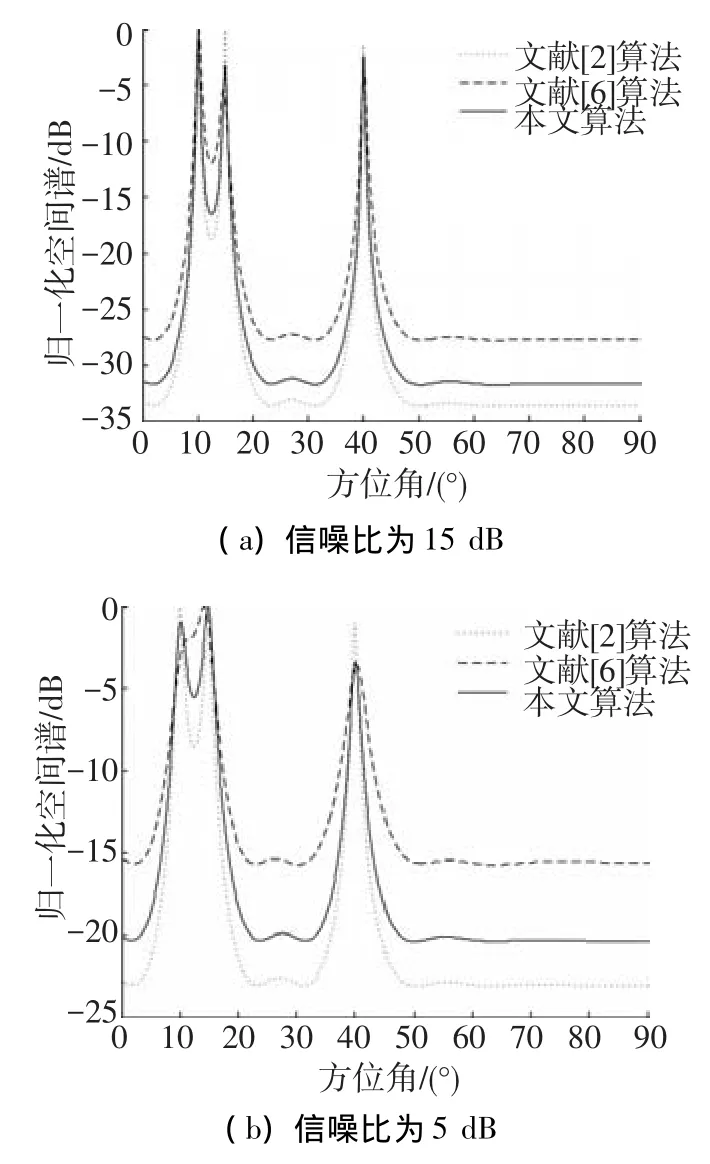
图2 3种算法不同信噪比的空间谱

3.3 DOA估计性能比较

假设2个不相关等功率窄带信号的入射角度分别为10°和20°，除信噪比和快拍数外，其他仿真条件同图2，考察3种算法的DOA估计均方根误差(Root Mean Square Error，RMSE)随信噪比和快拍数的变化，定义DOA估计的均方根误差为

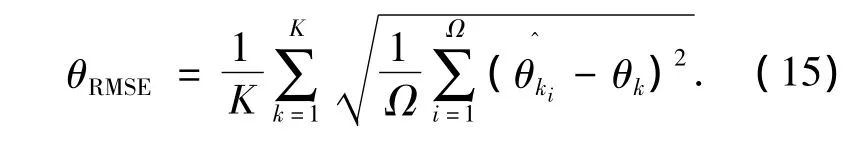
式中:K为信号数目表示每次运算得到的入射信号的DOA估计值，Ω为蒙特卡罗次数．

图3(a)、(b)分别表示入射信号DOA估计的均方根误差随信噪比和快拍数的变化曲线，其中带圆圈标记的为文献［6］算法的仿真结果，带方块标记的为文献［2］算法的仿真结果，带星号标记的为本文算法的仿真结果.在图3(a)中，快拍数为200，横轴为信噪比，从0 dB，间隔2 dB，变化到20 dB，纵轴为DOA估计的均方根误差，每一个信噪比数据进行500次蒙特卡罗独立统计.如图3(a)所示，与文献［6］算法相比，本文算法的θRMSE更小，当RSN＜14 dB时，两种算法的θRMSE差值较大，最大差值为0.25°，与文献［2］算法相比，算法θRMSE略大，两者的最大差值为0.12°，当RSN＞12 dB时，两种算法的θRMSE大致相等，这表明不同信噪比条件下，本文算法的DOA估计性能明显优于文献［6］算法，当信噪比较高时与文献［2］算法的DOA估计性能相当.在图3(b)中，信噪比为12 dB，横轴为快拍数，从50，间隔50，变化到500，纵轴为DOA估计的均方根误差，每一个快拍数进行500次蒙特卡罗独立统计.如图3(b)所示，本文算法的θRMSE比文献［6］算法小0.05°，而只比文献［2］算法大0.015°，且随着快拍数的增加，3种算法的θRMSE变化不大，与图2(a)结论相似，在不同快拍数条件下，本文算法的DOA估计性能明显优于文献［6］算法，与文献［2］算法性能相近.

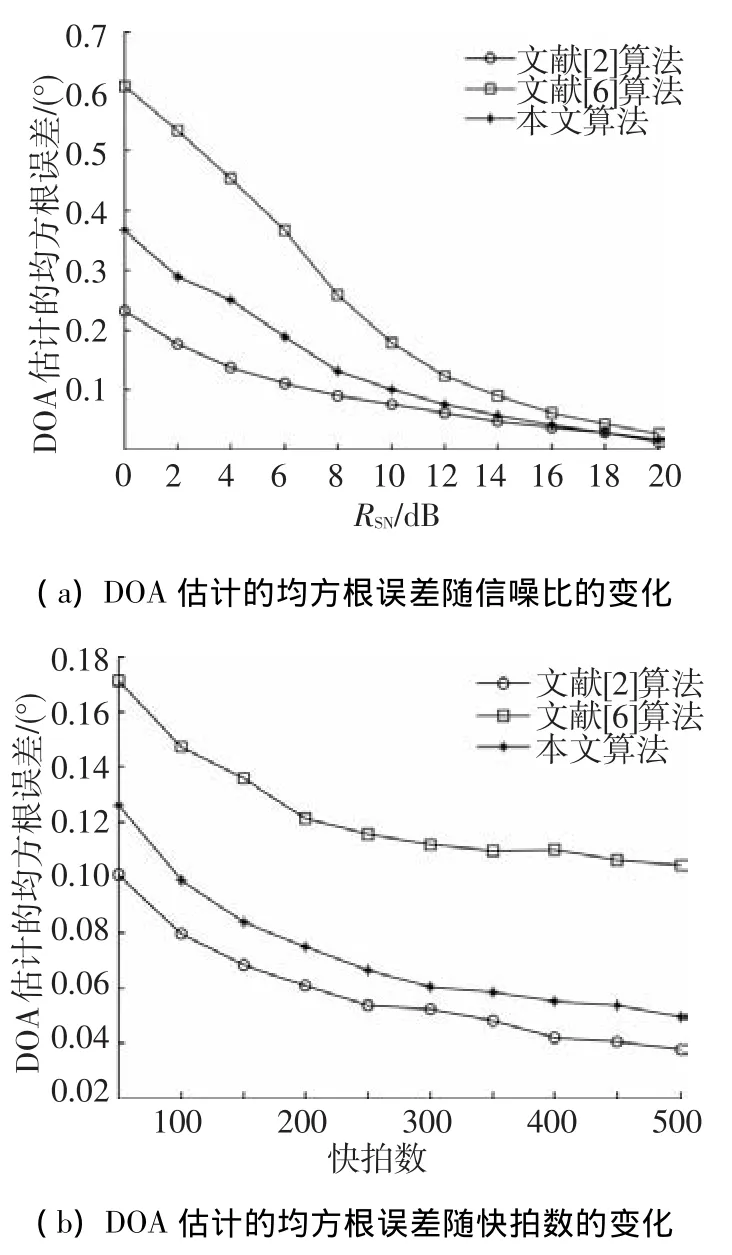
图3 DOA估计的均方根误差曲线

图2、3结果表明，与常规的MSWF算法相比，本文算法将声压振速联合信息处理思想应用到MSWF算法中获得了更高的DOA估计性能，且在高信噪比条件下，本文算法的DOA估计性能接近文献［2］算法，其原因是声压振速联合信息处理抑制了各向同性噪声，提高了声矢量阵的处理增益.相比MUSIC类算法，基于MSWF的DOA估计算法已在硬件中实现并拥有较好的DOA估计性能，故本文算法更易于工程实现.

4 结语

基于声压振速联合信息处理，本文选择参考阵元的电子旋转矢量作为MSWF算法的期望信号，证明了由声矢量阵观测信号的互协方差矩阵及观测信号与期望信号的互相关矢量构成的Krylov子空间等价于信号子空间，并运用MSWF算法快速求解 Krylov子空间的基.与常规的MSWF算法相比，本文算法在获得更高的DOA估计性能的同时，没有增加任何计算量;另外，本文算法的DOA估计性能稍逊于传统子空间类声矢量阵高分辨DOA估计算法，但是本文算法的计算量却大为减小，这更有利于工程实现，尤其信噪比较高或阵元数目较多时，本文算法优势明显.综上所述，本文算法在实现声矢量阵DOA估计中具有一定的工程应用前景.

［1］JOHAM M，SUN Y，ZOLTOWSKI M D，et al.A new backward recursion for the multi-stage nested wiener filter employing Krylov subspace methods［J］. Military Communications Conference，2001，2(5):1210-1213.

［2］姚直象，胡金华，姚东明.基于多重信号分类法的一种声矢量阵方位估计算法［J］.声学学报，2008，33(4):305-309.

［3］白兴宇，姜煜，赵春晖.基于声压振速联合处理的声矢量阵信源数检测与方位估计［J］.声学学报，2008(11)，33(1):56-61.

［4］姚直象，胡金华，姜可宇.矢量阵两类阵处理方法研究［J］.兵工学报，2012(9)，33(9):1138-1142.

［5］姚直象，姜可宇，郭瑞，等.基于声压振速联合处理的矢量旋转不变子空间方位估计方法［J］.北京理工大学学报，2012(5)，32(5):513-517.

［6］黄磊.快速子空间估计方法研究及其在阵列信号处理中的应用［D］.西安:西安电子科技大学，2005.

［7］安志娟，苏洪涛，包志强，等.一种新的基于Krylov子空间的快速子空间分解［J］.系统工程与电子技术，2009(1)，31(1):29-33.

［8］周天，杨程，李海森，等.基于AccelDSP的 MM-MUSIC算法实现及其在多波束测深声纳中的应用［J］.系统工程与电子技术，2011(12)，33(12):2613-2617.

［9］毛国华，王可人.一种基于DSP的快速MUSIC测向方法研究与实现［J］.电子信息对抗技术，2007(9)，22(5):10-13.

［10］王晓瑶，张国军，王盼盼，等.声矢量阵目标估计的新方法［J］. 传感器与微系统，2011(8)，30(8):73-76.

［11］庄学彬，陆名全，冯振明.一种数值稳健且低复杂度的信号子空间估计新方法［J］.电子与信息学报，2011(1)，33(1):90-94.

［12］刘红明，何子述，夏威，等.无参考信号条件下基于MSWF的 DOA 估计算法［J］.电子学报，2010(9)，38(9):1979-1983.

［13］JOHAM M，ZOLTOWSKI M D.Interpretation of multistage nested Wienerfilterin the Krylov subspace framework［J］.TechRepTR-ECE-00-51， Purdue University，USA，2000.