加强数学教材建设，提高大学生的创造能力

王 颖，李 红*，李厚彪

(电子科技大学 数学科学学院，成都 611731)

加强数学教材建设，提高大学生的创造能力

王 颖，李 红*，李厚彪

(电子科技大学 数学科学学院，成都 611731)

对如何提高学生创造能力的必要性，怎样加强数学教材建设进行了探讨。在高等数学教材建设中融入数学建模和发散思维思想对全面提高学生创造能力的重要意义。

高等数学;教材改革;数学建模;创造能力

知识创新和技术创新是知识经济的基本要求和内在动力。高校作为培养创新人才的重要基地之一，如何全面提高大学生的创新素质与创新能力，是每位教师应认真思考的问题。教材是从事教学活动的依据，是教学研究和教学改革的热点和核心问题之一。因此，教材建设对培养学生的创造能力有着举足轻重的重要作用。本文就教材建设中如何提高学生的创造能力问题进行探讨。

1 提高学生创造能力的必要性

创新素质主要由创新意识、创新思维、创造能力组成。美国著名教育家戴维斯(Davis)认为:创造能力包括“思维的流畅性，即产生大量设想的能力;灵活性，即对某个问题提出不同解法的能力;独创性，即提出不同、独到的设想的能力;精细性，即发展和装饰设想的能力;问题的敏感性，即发现问题，觉察缺少信息和提出恰当问题的能力;想象，即心理构图和驾驶设想的能力;隐喻思维，即一种设想和方案转换为另一种设想和方案的能力;评价，即估计方案适宜性的能力。”因此，创造能力可以说是一种综合素质，是一种积极开拓的状态，是一种潜能的迸发［1］。

数学作为一门研究现实世界数量关系和空间形式的科学，在它产生和发展的历史长河中，一直与各种各样的应用问题联系在一起。因此，从本源性上讲，数学最能激起人的自由创造本能［2］。而且现代社会要求培养的人才具有广博的知识，要能够分析并创造性地解决问题。因此，数学作为一门基础学科，不仅能传授一些已有的知识，更重要的是能培养学生发现规律、调整思维、把知识转化为自己的思维结果的创造能力。波兰学者科日艾布斯基(Korzybski)指出，人类的最大特征是“具有随着时代的节拍不断进步发展的性质，即具有发明发现和创意创新的能力，要启发人类独有的这种最高贵的性能，莫过于妥善利用数学教育。”因此，数学在培养人的创造能力中有着重要和突出的地位。

著名学者杨振宁在谈到中西方学生差异时也明确指出:“中国留学生学习成绩往往比一起学习的美国学生好得多，然而十年以后，科研成果却比人家少得多，原因就在于美国学生思维活跃，动手能力强和创新能力强。”因此，随着科学技术的不断发展，世界各国在发展道路上的竞争必然归结为科技人才创造能力的竞争。培养具有创造能力的高层次人才，对我国教育、科技发展具有重要的战略意义。

2 加强教材建设充分提高学生的创造能力

美国心理学家奥托(Otto Klineberg)指出:“我们所有的人都有惊人的创造力。”如何将这种潜在的能力转化成现实的能力，关键在于培养。

各种领域的创造能力都以理论思维为前提，创造能力源于理论思维能力的训练［1］。而教材是从事教学活动的依据，是理论思维能力的基础，并且数学学科是对理论思维能力要求比较高的一门学科。因此，加强教材建设(特别是数学教材建设)是培养学生理论思维能力、提高创造力的有效途径。那么如何加强教材建设呢?笔者认为在教材建设中应注意以下几点:

1)教材的改革要以促进和引导学生积极思考、主动探索、有效地进行数学认知活动为前提。教学是一项创造性劳动，教学方法和教材的创新会对学生创造力的培养有一种潜移默化的作用。数学知识不应仅靠传授获得，而应该引导学生自己去发现，独立地去掌握。美国卡内基教学促进会指出:“任何大学都不可能向学生传授所有的知识，大学教育的基本目标是要给学生提供终身学习的能力。”

2)从工科数学的角度看，学生创造精神、创新能力的培养主要是通过应用数学来体现。因此，在教材建设中要适当增加对实际工程背景的介绍和应用数学知识的实例。中国科学院李大潜院士指出:“数学的教学不能和其他科学和整个外部世界隔离开来，只是一个劲地在数学内部的概念、方法和理论中打圈子，这不利于了解数学的概念、方法和理论的来龙去脉，不利于启发学生自觉运用数学工具来解决各种各样的现实问题，不利于提高学生的数学素养。”［2］另外，科技人才学习数学的目的在于应用数学。因此，在教材中适当加入一些实际工程背景的介绍和应用数学知识的实例能不断提高学生应用数学的意识和兴趣，从而达到潜移默化地提高创新能力的目的。譬如在教材［3］中，针对各章知识，加入了10个具有实际工程背景的实例，如表1所示。

表1 具有实际工程背景的实例

3)在大学数学教材中融入数学建模的思想是提高学生创造力的一种有效途径。数学建模是联系数学和实际问题的桥梁，是数学转化为技术的重要途径，它已成为现代科技工作者必备的重要能力之一［4］。

目前许多高校都开设了数学建模课或数学建模培训班，并组织学生参加每年的全国数学建模或美国数学建模竞赛，使越来越多的学生受到了数学建模的教育。但数学建模教育实质上是一种能力和素质的教育，需要较长的过程，单靠开设一门选修课或培训课还远远不够。并且这种模式在许多情况下还是一种“精英教育”与我国高校扩招后的“大众化”教育还有一定的差距。因此，要全面提高大学生的素质，培养有创新精神的复合型应用人才，应从大学生普遍采用的数学教材入手，在其中融入数学建模的思想，这样才能使绝大多数的学生受益。李大潜院士指出:“在开设和改进数学建模课程的基础上，逐步将数学建模的精神，内涵和方法有机地体现到一些重要的数学课程中去，并在条件成熟时最终取消专门开设的数学建模类课程，或将其变为课外训练的辅助环节，应该是一个努力的方向。”［2］

数学建模对培养学生发散思维有重要的意义。发散思维是创造性思维的一种重要形式，其主要特点是思维的流畅性、变通性和独特性。它要求思维主体从多角度、多方面探索问题，并在一定时间内产生尽可能多的、与众不同且有成效的观念、想法。数学建模没有标准答案，对同一个问题可以采用不同的方法和思路建模，因此为培养学生发散思维和创新能力提供了广阔的空间，使学生受益匪浅。表1中的10个实例，实际上也是数学建模思想的体现。

4)在教材中适当加强数学试验和科学计算教育是对抽象的数学理论和数学建模思想有益的提高和补充。如今科学计算已成为与理论和实验相并列的三大重要科学研究手段，并已在实际生产中发挥着越来越重要的作用。数学方法与计算技术的结合已经形成了一种关键性的、可实现的技术。对于数学建模来说，在对一个实际问题建立出数学模型后，需要对数学模型进行实验验证，并根据实验结果做进一步的修改和完善，如此循环多次才能解决问题。因此，若没有可靠、坚实的数学试验和科学计算技能，再好的数学模型也不一定能解决实际问题。另外，现在的数学理论也越来越抽象，在教材中适当加入一些数学实验和计算的内容，有助于学生对数学的理解和掌握，并且可提高学生的学习兴趣和动手能力，从而提高其创造力［5-7］。

5)根据教学对象的不同，对教材分层设计与分层次教学，对于充分提高不同层次学生的创造能力有着明显的效果［8］。高校扩招推动了高等教育由“精英教育”向“大众化教育”的转变，也带来了学生生源分布广、水平参差不齐的新问题。如何因材施教、充分提高各层次学生的学习兴趣和创新活力，是目前大多数综合型大学面临的重要教学问题。加强教材的分层次设计，以学生为本，因材施教、分层教学、分流培养已成为许多学校的共识和有效的办学经验［9］。

6)应注意教材中课后习题的设计和试验设计建设［10］。习题是数学教材的重要组成部分，是学生进行有效学习的重要载体。在教材改革实践中，有些教师比较重视例题的教学，却忽视对教材习题的精细化研究，以致习题的功能被弱化，习题中隐含的一些有价值的因素未能被充分开发与利用。事实上，优化分层设计使用教材习题，对提高学生的创造能力大有裨益。譬如，北京大学数学系丁石孙、王萼芳和石生明等编写的《高等代数》教材已历40多个春秋至今畅销不衰，这与其精深的习题设计不无关系。另外，在国外许多经典的教材中，对习题和试验的设计也是精益求精。如 L.W.Johnson［11］和 R.Horn［12］的教材等等。

针对目前国内高等数学教材中涉及应用方面的习题较少、课后作业题型单一的问题，可通过改革其问题形式，进行优化处理。可选取一些综合性和趣味性且与其他学科相关或切合实际生活的开放性应用题(如图1～2所示)，让学生独立或组成小组，利用解析方法或计算机数值计算共同完成［5-7］。通过完成这种作业，使学生感受到数学应用之所在，同时也培养了学生的团队协作精神和探究与解决问题的能力。李大潜院士大力提倡和推动以问题而不是以文献驱动的应用数学研究:“外部矛盾的驱动和内部矛盾的驱动是数学发展的双翼，是相互联系和促进的，都是必不可少的。”［2］

图1 成都市旅游路线用户交互界面［8］

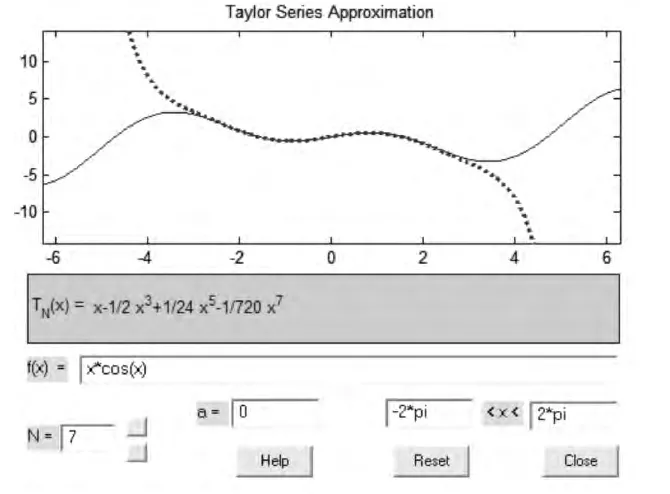
图2 泰勒级数逼近模拟工具箱taylortool［10］

加强教材建设应避免教材太难或太易的误区。因此，任何“拔苗助长式”或“填鸭式”的教材都不切合实际。另外，随着数字技术、多媒体技术、网络技术的快速发展，教材已经由单一的纸介教材发展为音像制品、电子教案、电子图书、网络课程等多种形式。教材立体化建设也越来越受到人们的重视，被世界各地的教育工作者广泛接受。

总之，时代需要创造型人才，而创造型人才的培养需要创新型教育。在教育中，除了教师、学生和设备之外，重要的条件就是教材。因此，学校各科教学(特别是数学学科)均应以加强学生创造能力的培养为核心，在教材中适时、合理地渗透创造性思维能力训练。

3 对引进国外教材的几点看法

长期以来，我国通用的高等数学教材体系比较单一，基本上取材于前苏联20世纪50年代的工科数学教材，强调传授知识的效能，安排紧凑，逻辑紧密，而现代技术相对较少。近年来引进的美国数学教材，注重传统与创新的结合，重视实际应用，习题和教学配套资源丰富，并且渗透现代先进技术特别是计算机技术的使用，对教师要求比较高。这2种教材各有优势，具有较强的互补性。

笔者认为，在教材建设上，借鉴和采用个别的外文教材是可取的，但也不能以偏概全，全盘西化，为了技术而技术。比如在教材的编写上，很多美国教材对概念和定理的讲解都采用了“几何—分析—语言—数值验证”的模式，这对我们是一个很好的启发。但正如 James Stewart［9］指出:“技术(计算机技术)的运用可以极大地激发学生的注意力，使他们成为主动的学习者。但是，这里存在着不当使用的潜在危险。……重要的是需恰当使用，所谓‘恰当’的标志是实现技术和微积分的相互作用(interaction)。简言之，技术不是包治百病的灵丹妙药，但如恰当使用，可以有力地促进学习。”因此，在教材建设上我国应走自己的路，建立适合中国国情的具有鲜明中国特色的教材队伍。［8］

总之，教材建设是教学改革的核心和重中之重。教材改革涉及到方方面面，是一个复杂的体系。如何充分发挥教材在培养学生创新能力中的作用是一个关键问题。各教材之间要相互协调，各有侧重，和谐发展，才能更好地发挥出教材的优势，培养出杰出的创新人才。

［1］毛京中.创新力的培养与工科数学教学的创新［J］.大学数学，2003，19(1):51-53.

［2］李大潜.大力提倡和推动以问题驱动的应用数学研究［C］//第二届大学数学课程报告论坛论文集.北京:高等教育出版社，2007:3-7.

［3］黄廷祝，成孝予.线性代数与空间解析几何［M］.3版.高等教育出版社，2008.

［4］萧树铁，谭泽光，曹之江，等.面向21世纪大学数学教育改革的探讨(续三)［J］.高等数学研究，2001，4(2):6-10.

［5］钟俊达，吴云云，李厚彪.Matlab-GUI在旅游路线优化上的应用［J］.实验科学与技术，2013，11(4):39-41.

［6］李厚彪，钱思远，修成竹，等.基于Matlab的大学数学综合实验设计研究［J］.实验科学与技术，2012，10(6):201-203.

［7］李红，李厚彪，蒲和平.借助软件在《高等数学》中进行实验教学［J］.实验科学与技术，2012，10(6):292-295.

［8］黄廷祝，傅英定，成孝予.国家精品课程“线性代数与空间解析几何”的建设［J］.大学数学，2006，22(2):14-16.

［9］吴志坚.美国数学教学改革的回顾与展望［C］//第二届大学数学课程报告论坛论文集.北京:高等教育出版社，2007:51-57.

［10］郭镜明.关于借鉴美国微积分教材的一点思考［C］//第二届大学数学课程报告论坛论文集.北京:高等教育出版社，2007:69-75.

［11］JOHNSON L W.Introduction to linear algebra［M］.5 edition.Upper Saddle River:Prentice-Hall，Inc.，2000.

［12］HORN R，JOHNSON C R.Topics in matrix analysis［M］.New York:Cambridge University Press，1991.

Strengthening Mathematical Textbook Construction to Fully Enhance Students＇Creative Ability

WANG Ying，LI Hong*，LI Houbiao
(School of Mathematics Sciences，University of Electronic Science and Technology of China，Chengdu 611731，China)

This paper mainly discusses the necessity for mathematical teaching material construction in order to enhance students’creative ability，and some previous experiences are summarized in terms of how to strengthen mathematics textbook construction.The corresponding importance is also discussed on the integration of mathematical modeling and divergent thinking idea into the construction of higher mathematics textbook to comprehensively improve students’creative ability.

Higher mathematics;textbook Reform;Mathematical Modeling;Creativity

O151.2

A

2095-5383(2014)02-0108-03

10.13542/j.cnki.51-1747/tn.2014.02.034

2014-01-02

电子科技大学教改项目“面向创新能力培养的大学数学课程资源建设与实践”(2013XJYSL026);研究生教研教改子课题“‘数值代数’课程内容及体系全面改革”(Y03003023901002010)

王颖(1979-)，女(汉族)，四川雅安人，副教授，博士，研究方向:偏微分方程。

李红(1979-)，女(汉族)，四川广汉人，硕士，讲师，研究方向:微分方程与动力系统理论，通信作者邮箱:sichuanhong@163.com。