基于反射系数测量的黏弹性材料动态力学参数反演方法
陶 猛,赵 阳
(1.贵州大学 机械工程学院,贵阳 550025;2.上海交通大学 机械系统与振动国家重点实验室,上海 200240)
以黏弹性介质为基底材料的声学覆盖层,其动态力学参数与声学性能存在定量关系。声学覆盖层的吸声、隔声等性能预报除了要采用合理的计算分析模型外,准确的黏弹性动态力学参数也是必不可少的。在不同的温度、频率和静水压力条件下,黏弹性材料表现出不同的力学特性,因此要想准确测量黏弹性材料动态力学参数并不容易。
通常测量动态力学参数的方法可分为两大类,一类是基于振动响应测量动态力学参数[1-4],比较常用的有强迫非共振法、振动梁法、动态黏弹谱仪法。尽管这些测试方法都相对简单,但是这些方法都有各自的局限性,例如振动测试方法的频段较低,或者基于时温等效原理推导的杨氏模量还没有直接的测试结果加以验证等。另一类是通过测量材料声学特性反演材料动态力学参数的方法,这样可在频段范围上与机理研究同步。已有方法包括在水池中由待测材料的平板试样测量斜向入射声波的回声降低或插入损失来反演材料的剪切特性[5-6],但低频测量时由于样品边缘的衍射干扰使得误差较大。此外,也有利用做成球形的待测材料试样,使实际测量的散射系数与理论计算的散射系数误差最小以计算材料体积模量的方法[7]。
本文研究了一种通过测量圆柱空腔覆盖层的反射系数,来反演黏弹性材料动态力学参数的方法。由于平面波垂直入射到圆柱空腔覆盖层时,其反射系数与其结构、材料参数具有明确的解析关系,因此首先利用该关系建立动态力学参数的反演过程。需要指出的是,动态力学参数如杨氏模量、剪切模量和泊松比等可通过材料的纵波声速和剪切波声速换算得到,因此该方法的核心是反演纵波声速和剪切波声速这两个基本参数。然后,以某种橡胶制成的圆柱空腔覆盖层样品为例,进行了声管测量和结果分析。
1 声学覆盖层反射系数的计算模型
圆柱空腔声学覆盖层的结构是沿厚度方向形成空腔,空腔的基本形状是圆柱型空腔,图中按照正三角形周期性地排列了同样的空腔,由于对称性可以只取其中的一个单元分析,但是建立六面棱柱体的理论模型相当困难,可用圆柱代替以简化模型的复杂性,这样就得到黏弹性圆柱管的模型,如图1所示,其中黏弹性圆柱管的外半径为a,内半径为b。
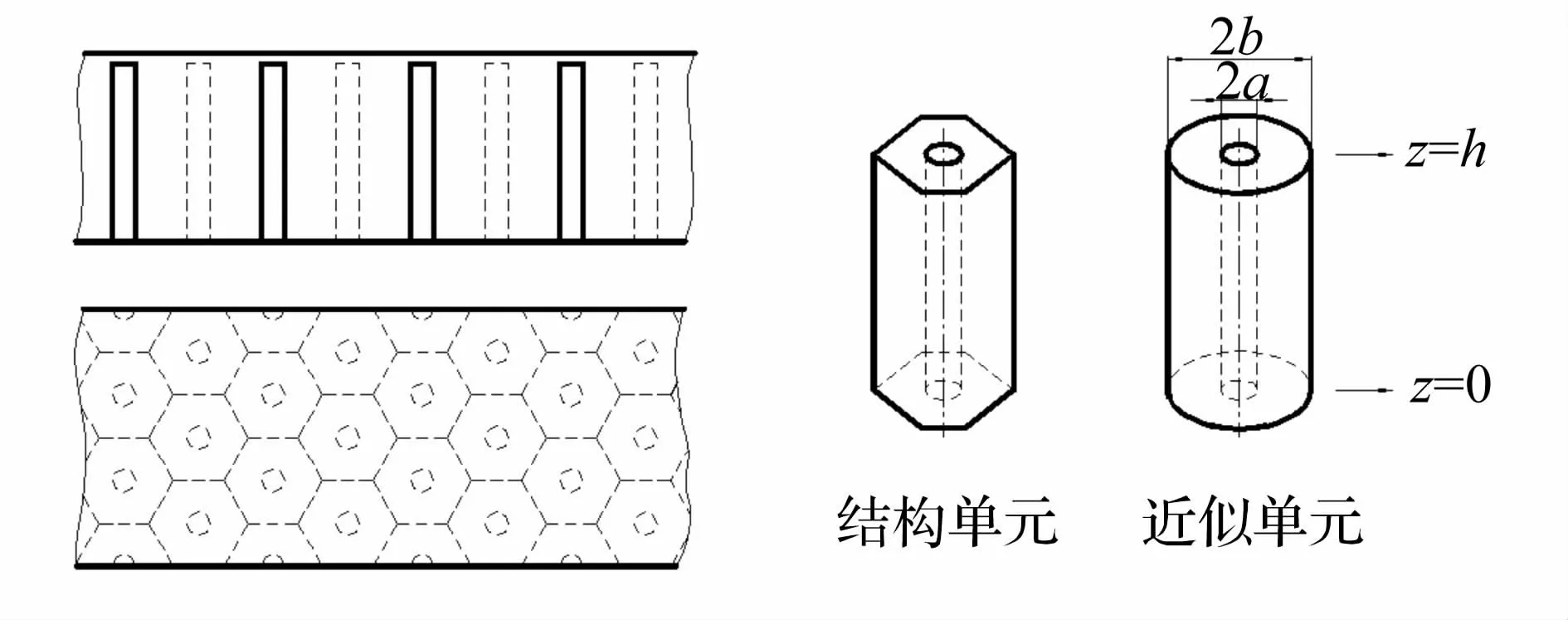
图1 周期结构圆柱空腔覆盖层的结构示意图Fig.1 Configurations of the acoustic layer embedded periodic cylindrical-hole
汤渭霖等[8]建立的圆柱空腔覆盖层的二维理论将声学覆盖层的单元简化为黏弹性圆柱管,其声学特性取决于波在圆柱管中的传播和损耗特性。但是该模型考虑了高阶轴对称波对声学特性的贡献,使得计算和分析过程相当复杂繁琐。因此,有必要基于二维理论寻找一种合理快速的近似方法,而这种方法主要基于以下近似:平面波垂直入射时,圆柱空腔覆盖层的低频性能由黏弹性圆柱管中的最低阶轴对称波的传播特性决定[8],进而黏弹性圆柱管的等效阻抗可由最低阶轴对称波的传播波数确定。
假设在声波小振幅激励的情况下,采用Kelvin-Voigt线性黏弹性模型来描述声学覆盖层的基底材料,可以得到与弹性模型形式相同的方程和解,区别在于将弹性常数换成相应的黏弹性常数。圆柱管中轴对称波的形式解一般可以写成[8](省略时间因子 ejωt):
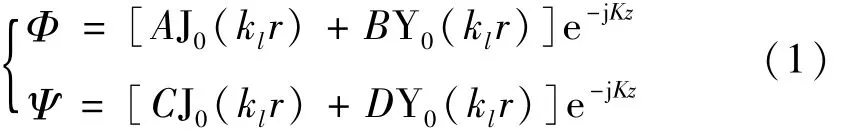
式中:分别是径向纵波波数和径向剪切波波数,K是轴对称波波数,c槇l和分别是黏弹性材料的复纵波声速和复剪切波声速。
在圆柱坐标系下,黏弹性圆柱管的位移和应力可用两个标量势函数及其导数来表示。在平面波入射条件下,通过对黏弹性圆柱管内、外边界建立合理的边界条件,可以获得描述轴对称波的特征方程:

其中:

式中:Jn(·)和 Yn(·),(n=0,1)分别是 Bessel函数和Neumann函数。特征方程(2)式的详细建立过程可参见文献[8]。对于给定的结构参数和材料属性,求解式(2)可以得到一组复根 Km(m=1,2,…),并由此确定 kl,n和 kt,m。
另一方面,在只考虑最低阶轴对称波模式的条件下,无限长黏弹性圆柱管中的等效阻抗可以写成如下形式[9]:

这样,黏弹性圆柱管前端面(z=h,下标f表示)和后端面(z=0,下标b表示)处的位移和应力就可通过传递矩阵T联系起来,即:

当黏弹性圆柱管后端面(也即是背衬)的阻抗Zb已知时,前端面的表面阻抗可以根据式(5)得到:
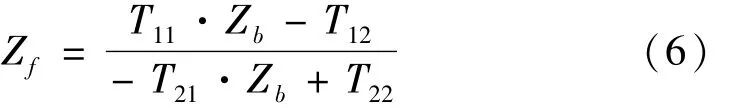
声学覆盖层的反射系数可由下式计算:

式中:Z0是水介质的特性阻抗。
2 复纵波声速和复剪切波声速的求解算法
实际黏弹性材料的动态力学参数与频率呈现明显的相关性,因此通过单个样品在已知背衬条件下的测量能够获得不同频率处的一组反射系数,但是显然无法通过单次测量同时获得复纵波声速和复剪切波声速两个未知的基本参数。因此,至少需要两组反射系数的测量数据,才能计算黏弹性材料的复纵波声速和复剪切波声速,这可以通过以下两种途径获得:①通过测量两组不同结构参数的声学覆盖层在同一背衬条件下的反射系数;②通过测量单个声学覆盖层在不同背衬条件下的反射系数。除此之外,理论上还可以测量更多不同条件下的反射系数,两两组合求解相应的复纵波声速和复剪切波声速,然后根据最小二乘法拟合得到最终参数,并进而计算其它的黏弹性动态力学参数。
根据两组实测的反射系数来求解复反射系数和复剪切波声速的问题,本质上就是求解二元非线性方程组。由于是非线性方程且包含复宗量,因此采用牛顿迭代法[10]来解决这个问题较为合适,对于形如下式的二元非线性方程组:

其迭代公式为:

式中:
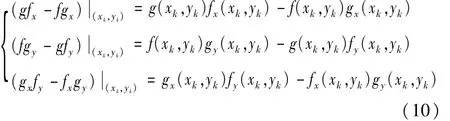
通过上式可迭代出 k=1,2时,(xk,yk)的值,当≤ε(ε>0为设定的误差控制项)时,即可获得方程组的根(xk,yk),其中通常可以选择经验值或者常用值作为初始变量。
因此,对于同一个圆柱空腔覆盖层样品,完成两组已知的不同背衬条件(如钢背衬和空气背衬)下的反射系数测量,即可建立求解复纵波声速和复剪切波声速的方程组:

式中:R(,)表示根据上节模型计算的反射系数,R表示实验测量的反射系数,下标b1和b2分别表示两组不同的背衬条件。
获得复纵波声速和复剪切波声速后,即可计算黏弹性材料的复拉梅常数和复剪切模量:

对于线性黏弹性材料,另外一组常用材料参数的表达形式是利用复弹性模量和复泊松比来表示,这组参数可以利用线性黏弹性材料的本构关系来计算:
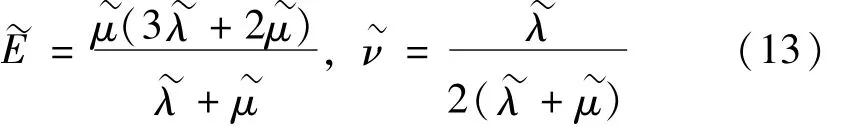
3 动态力学参数的计算结果及讨论
采用上节所述第(2)种途径来求解计算黏弹性材料的动态力学参数,在水声声管中对以某种橡胶材料制作的圆柱空腔声学覆盖层样品进行了反射系数的测量,测量方法选择成熟的传递函数法[11],两种背衬条件分别为硬背衬和空气背衬。根据测量结果对橡胶材料的黏弹性动态力学参数进行了计算,其中橡胶密度为1 210 kg/m3,圆柱空腔半径为2 mm。
图2表示橡胶材料复纵波声速和复剪切波声速的测量结果。复纵波声速可改写成=cl(1+jηcl)的形式,复剪切波声速可改写成=ct(1+jηct)的形式,其中cl和ct分别表示复纵波声速和复剪切波声速的实部(图 2(a)),ηcl和 ηct分别表示相对应的损耗因子(图2(b))。由于水声声管的截止频率限制,有效的测量数据局限在中频范围内。从图2(a)可以看出,纵波声速约在2 000 m/s~2 100 m/s的范围内变化,而剪切波声速在在该频段范围内的变化不大,约为180 m/s。从图2(b)不难发现,由于纵波损耗因子很小,因此可忽略不计;剪切波损耗因子明显大于纵波损耗因子,并且剪切波损耗因子呈现出一定的频散关系。
图3表示橡胶材料复拉梅常数和复剪切模量的测量结果。复拉梅常数可改写为=λ(1+jηλ)的形式,复剪切模量可改写为=μ(1+jημ)的形式,其中λ和μ分别表示复拉梅常数和复剪切模量的实部(图3(a)),ηλ和 ημ分别表示相对应的损耗因子 (图3(b))。一方面,从图2(a)可知该橡胶材料的剪切波声速远小于纵波声速,通过(12)式计算的过程中,剪切波声速对计算结果的影响很小,因此可以忽略不计,拉梅常数主要反映了材料的纵向特性。另一方面,根据线弹性理论,材料的剪切模量和杨氏模量之间满足关系E=2μ(1+ν)。对于橡胶类的黏弹性材料,其泊松比接近于0.5,所以杨氏模量实部基本上是剪切模量实部的3倍,而杨氏模量损耗因子与剪切模量损耗因子基本相同,也就是说杨氏模量实部及其损耗因子的频散曲线基本表现出与剪切模量实部及其损耗因子频散曲线类似的规律,因此不再单独给出杨氏模量的测量结果。

图2 橡胶的复纵波声速和复剪切波声速Fig.2 Complex longitudinal and complex transverse wave speed of rubber

图3 橡胶的复拉梅常数和复剪切模量Fig.3 Complex Lame constant curves and complex shear modulus curves of rubber
除此之外,由于本文讨论的黏弹性材料动态力学参数测量方法的基础是测定空腔覆盖层的反射系数,因此实验过程中的误差不可避免地会影响后续计算结果的准确程度。实验过程中的误差来源主要有两大类:一是样品加工制作带来的误差,如空腔实际大小或空腔间距与设计尺寸有差别;二是测试系统本身存在的误差对测试结果的影响,如两个水听器的相位和幅值是否完全一致,实际背衬条件与理想背衬条件(如绝对硬背衬)的差别等。
图4和图5分别表示圆柱空腔半径的实际尺寸和设计尺寸不相同时,对部分黏弹性动态力学参数测量结果的影响。从图中可以看出,若空腔实际半径比设计尺寸增加10%(图5和图6中的红线)时,测量得到的复杨氏模量实部误差约为17%且小于真实数值,复泊松比实部误差约为0.12%且大于真实数值;若空腔实际半径比设计尺寸减小10%(图5和图6中的蓝线)时,测量得到的复杨氏模量实部误差约为19%,复泊松比实部误差约为0.13%,从以上结果反映了空腔实际尺寸的误差对杨氏模量的测量结果影响较大,而对泊松比的影响较小。
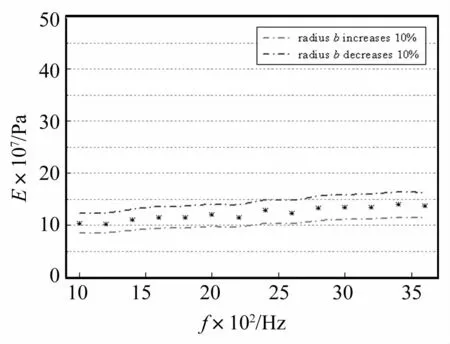
图4 橡胶的杨氏模量及其误差范围Fig.4 Young’s modulus and associated error of rubber
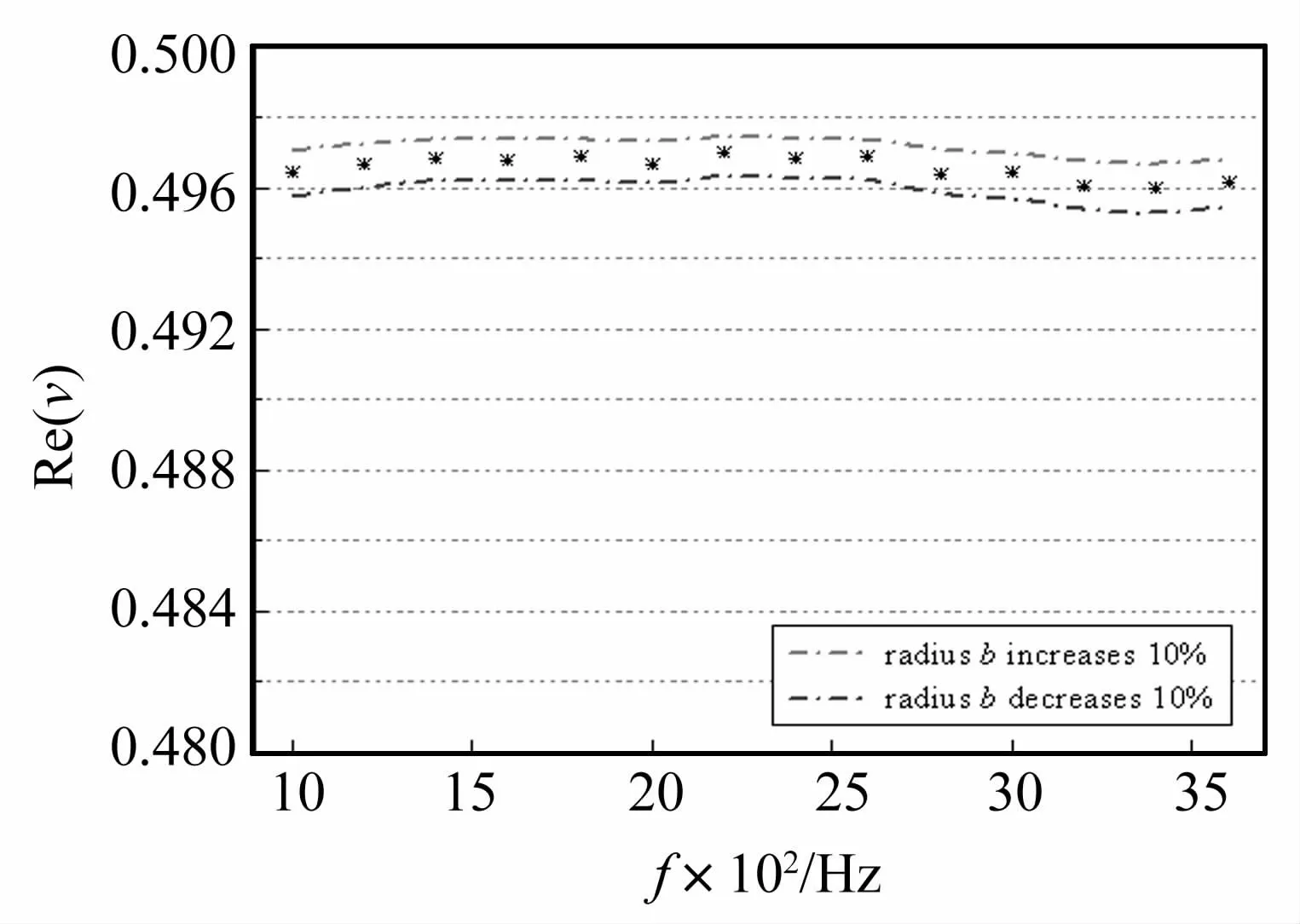
图5 橡胶的泊松比及其误差范围Fig.5 Poisson’s ratio and associated error of rubber
4 结 论
本文提出了一种以测量圆柱空腔覆盖层反射系数为基础、采用解析法反演黏弹性材料动态力学参数的方法,其特点是能够与覆盖层声学性能测试同步进行,便于声学覆盖层的特性分析和优化设计。采用该方法测量动态力学参数至少需要测量两组不同工况的反射系数,当然也可以完成更多工况条件下的测试,然后两两组合得到相应的参数测量结果,通过拟合获得最终的黏弹性动态力学参数。此外,由于测试声管的截止频率限制,文中对于材料参数的分析局限于中频范围,而本文提出的方法原则上也适用于高频情况,如可采用脉冲法测量覆盖层的反射系数,进而拓宽动态力学参数测量的频率范围。
[1]Boiko A V,Kulik V M,Seoudi B M,et al.Measurement method of complex viscoelastic material properties[J].International Journal of Solids and Structures,2010,47(3):374-382.
[2]Liao Y,Wells V.Estimation of complex Youngs modulus of non-stiff materials using a modified Oberst beam technique[J].Journal of Sound and Vibration,2008,316(1-5):87-100.
[3]Liu H W,Yao L,Zhao H,et al.A mixed method for measuring low-frequency acoustic properties of macromolecular materials[J].Science in China Series G:Physics,Mechanics and Astronomy,2006,49(6):729-739.
[4]尹铫,刘碧龙,白国锋,等.激光测振有限元反演优化方法测量黏弹性料动态力学参数[J].声学学报,2013,38(2):172-180.YIN Yao,LIU BI-long,BAI Guo-feng,et al.A study on polymer modulus test using laser-based finite element method[J].Shengxue Xuebao,2013,38(2):172-180.
[5]李水,唐海清.水声材料横波声速和衰减系数参量源法测量系统[J].声学学报,2005,30(4):317-323.LI Shui, TANG Hai-qing. A system for measuring the transverse wave velocity and attenuation coefficients of underwater acoustic materials in parametric source method[J].Shengxue Xuebao,2005,30(4):317-323.
[6]Piquette J C.Shear property determination from underwater acoustic panel tests[J].Journal of the Acoustical Society of America,2004,115(5):2110-2121.
[7]宋扬.中高频段下黏弹性材料声学参数测量[D].哈尔滨:哈尔滨工程大学,2007.
[8]汤渭霖,何世平,范军.含圆柱形空腔吸声覆盖层的二维理论[J].声学学报,2005,30(4):289-295.TANG Wei-lin,HE Shi-ping,FAN Jun.Two-dimensional model for acoustic absorption of viscoelastic coating containing cylindrical holes[J].Shengxue Xuebao,2005,30(4):289-295.
[9]Tao Meng. Simplified model for predicting acoustic performance of an underwater sound absorption coating[J].Journal of Vibration and Control, doi: 10.1177/1077546312461027(Published online).
[10]徐瑞民.二元非线性方程组求根的牛顿迭代法[J].山东轻工业学院学报,2009,23(4):89-91.XU Rui-min.Newton’s method for the nonlinear function of two independent variables[J].Journal of Shandong Institute of L Light Industry,2009,23(4):89-91.
[11]朱蓓丽,肖今新.双水听器传递函数法低频测试及误差分析[J].声学学报,1994,19(5):351-360.ZHU Bei-li, XIAO Jin-xin. A two-hydrophone transfer function method for measuring low-frequency acoustic properties and its error analysis[J].Shengxue Xuebao,1994,19(5):351-360.

