囊式空气弹簧载荷建模与实验研究

成小霞，李宝仁，杨 钢，杜经民

（华中科技大学 FESTO气动中心，武汉 430074）

由于具有固有频率低、承受载荷能力大，刚度、阻尼、输出载荷、工作高度等参数均可以根据需要设计等很多优点，空气弹簧作为隔振器越来越广泛地被应用到车辆、机械设备及特殊装置隔振系统中。载荷计算是空气弹簧静动态特性分析的理论基础，也是实际隔振系统设计的依据，因此对空气弹簧的载荷特性进行深入研究，得到准确度高、实用性强的载荷模型就显得尤为必要。国内对空气弹簧特性的研究较多，主要采用的方法有试验法、有限元法和图解法［1－2］。试验法简单但需要专门的设备，有限元方法基于材料和结构参数能够准确获取的前提，故这两种方法均具有较大的局限性，不适合空气弹簧隔振系统的计算分析。现有的基于图解法的计算空气弹簧载荷的模型只是考虑了形状、几何尺寸、工作气压等参数和载荷的关系［3－4］，而忽略了囊体材料特性对载荷性能的影响。本文以囊式空气弹簧为具体研究对象，在详细分析囊体材料特性的基础上，推导出基于材料非各向同性特性的新载荷模型。该模型充分考虑了囊体材料特性对载荷输出的影响，能够更加准确地描述空气弹簧的载荷特性。

1 囊式空气弹簧静态特性建模

空气弹簧通过囊壁挠曲实现工作高度的改变，在振动过程中囊壁和上下盖板连接处会产生接触问题。考虑到接触状态的复杂性，建立空气弹簧载荷模型时需要对问题进行简化，并引入一些适当的假设：①囊壁自身重力与空气弹簧输出力相比较很小，可忽略不计；②工作过程中，轴向和径向囊壁在自然状态下假设始终保持圆弧形状；③假设囊内气体是理想气体，静态加载过程为等温加载。

囊式空气弹簧结构如图1所示。

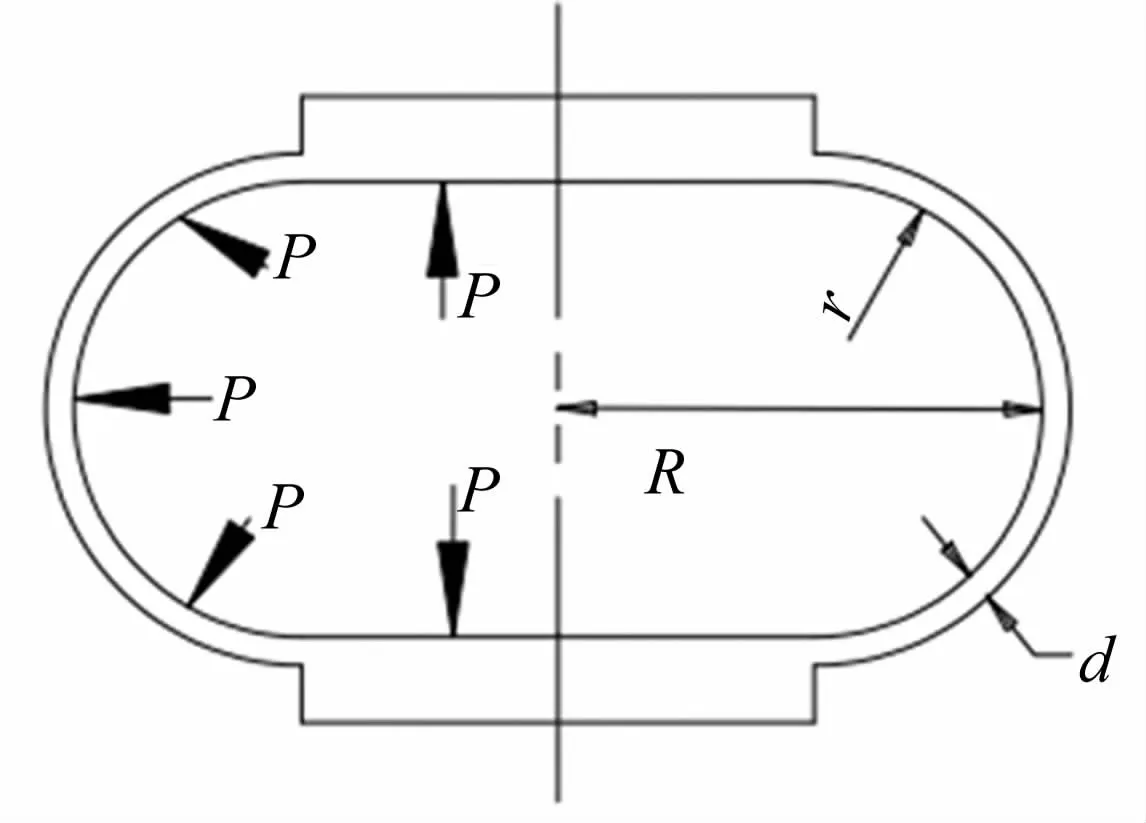
图1 空气弹簧结构示意图Fig．1 Air spring structure

1．1 空气弹簧弹性力分析

对空气弹簧进行受力分析，得其平衡方程［5］：

式中：p为囊内气体工作压力（表压），d为囊壁的厚度，R为囊体的最大径向半径，r为囊壁轴向圆弧半径，σs为赤道面囊壁材料垂向正应力。

选取赤道面囊壁上的一微元体进行应力分析，微元体结构见图2所示。dθ、dψ为 微 元 体 轴向、径向圆弧角度；dps为垂向应力 σs作用在截面上的弹性力，dpu为周向应力σu作用在截面上的弹性力。

图2 微元体结构示意图Fig．2 Element structure

微元体在dPs、dPu径向的分力和内部气压力共同作用下处于平衡状态，其径向平衡方程为：

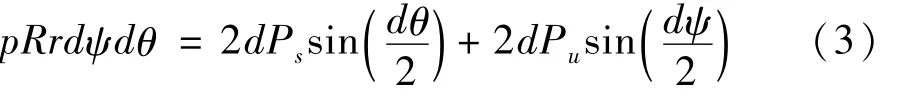
把式（2）代入（3）式并化简得：

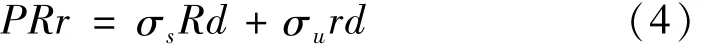
1．2 囊壁特性分析

空气弹簧囊体由橡胶和帘线复合硫化而成，内外层橡胶起密封和保护作用，空气弹簧内部的压力主要由中间帘线层来承担。已有研究结果表明，帘线的材质、粗细、排列密度、角度、铺设层数、铺设顺序和橡胶层材质、厚度等参数对囊壁应力都有一定的影响［6］，进而直接影响到空气弹簧的静动态特性。由于橡胶和帘线的材料特性异同以及其复杂的构造方式，囊体材料整体表现出复杂的各向异性特性，同一囊体材料轴向和径向的弹性模量不相同，而同一方向囊体材料不同弹性模量也不全相同。考虑到囊体弹性模量表达式复杂且很多具体参数无法获得，为了简化计算，引入系数u来表示囊体的这种综合的各向异性材料特征。系数u定义为轴向弹性模量Es和径向弹性模量Eu的比值，u不仅可以表示同一囊壁轴向径向弹性模量的差异大小，同时也可以表示不同空气弹簧囊体的材料特征。根据理论研究，u一般在0．8～2之间取值，可以通过计算值和实验值拟合得到，具体计算方法后面介绍。

囊体材料在变形过程的应力与应变呈非线性关系，但在应变ε＜15%的范围内可近似认为是线性的［7］。从材料疲劳强度考虑，空气弹簧设计的允许工作行程范围内材料应变量都不会超过此范围，所以可认为空气弹簧工作过程中囊体材料应力与应变之间服从虎克定律。假设在内部气压作用下，微元体在垂向和周向产生相同的变形量Δr＝ΔR，则垂向和周向应力之间存在如下关系：

综合式（1）、（4）、（5）可得输出力表达式：

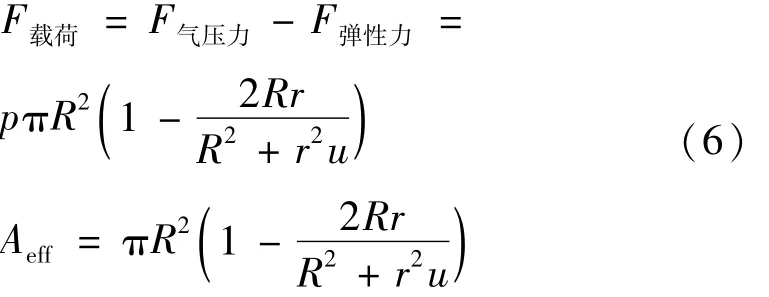
Aeff为空气弹簧有效面积，定义为加载到空气弹簧上的载荷与空气弹簧内部空气压力相平衡时的断面积。有效面积是一个理论等效值，而非接触面积（盖板面积）或承压面积（最大径向面积）。很多文献中给出有效面积计算公式却没有给出依据［8］；有的文献中认为承压面积就是有效面积，或是假设有效面积在一定高度范围内为定值，这些处理方法都会带来一定的误差，这一点在后面有对比说明。

2 数值仿真

2．1 数值计算

考虑到帘线层弹性模量较大，囊壁在压缩或拉伸变形时，材料产生的变形量与工作高度相比较可忽略不计，所以假设变形过程中囊壁轴向圆弧长度保持不变。

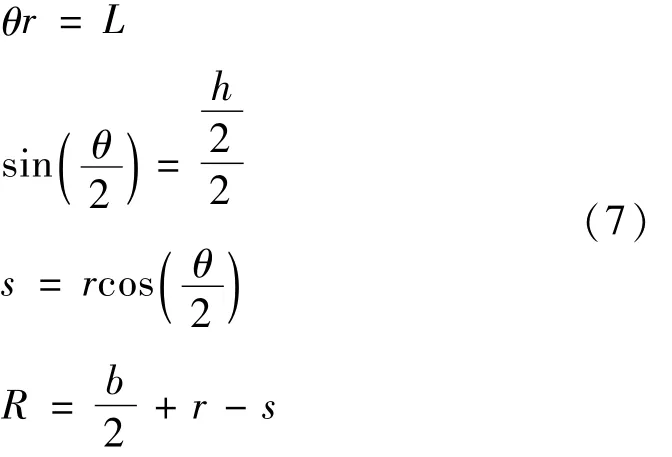
采用几何图解的方法对空气弹簧的工作参数进行计算。其参数满足以下几何关系：式中：h为空气弹簧的工作高度，L为囊壁圆弧长度，θ为囊壁圆弧角度，b为上盖板直径，R、r定义和图1中相同，s为r在R上的投影值。

由式（7）可得到空气弹簧的重要参数R，r，其为关于高度h的函数。将R、r值带入载荷表达式进行数值仿真，可以得到载荷F关于工作高度h、气体压力p的曲线。

2．2 仿真结果分析

首先对空气弹簧的输出力与工作高度、压力的关系进行仿真，结果如图3所示。从图中可以看出，空气弹簧静态载荷为一簇非线性曲线。工作高度恒定时，压力越大，承载力越强；工作压力恒定时，压缩程度越大（高度越低），承载能力越强；且随着工作压力升高，非线性特性越明显。

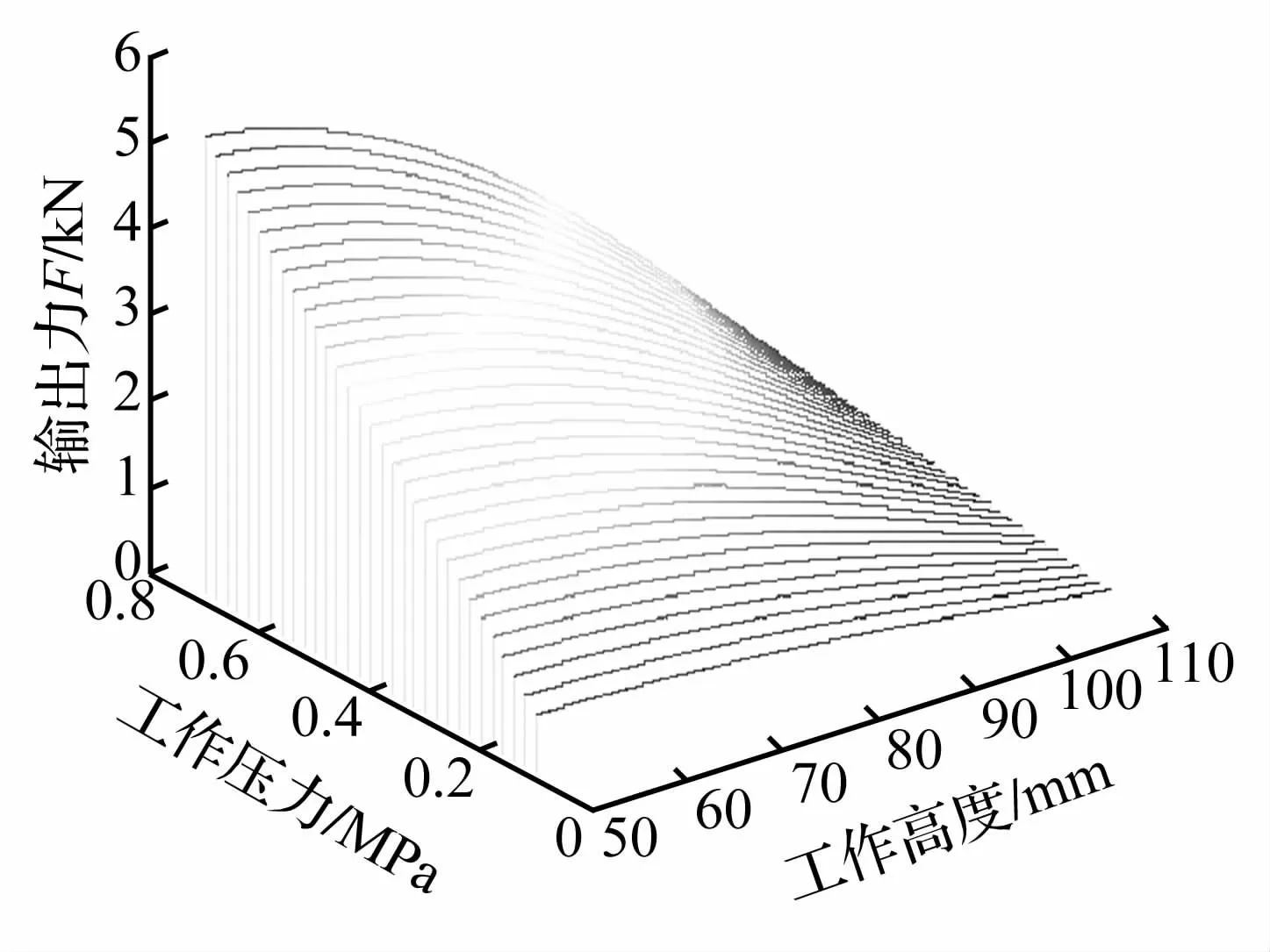
图3 空气弹簧输出力－高度－压力关系曲线Fig．3 The relation of force output to height and pressure

图4 囊体材料对空气弹簧输出力影响Fig．4 Influence of bag material on force output

图4 为0．1～0．7MPa下，模型考虑材料特性前后输出力曲线。图中可看出，考虑囊体材料特性后对输出载荷有一定的影响，在压缩状态下的影响不是很大，但是在拉伸状态下两种模型的区别较明显。这是因为在压缩状态时承压平面半径R较大，此时气压力起主要决定作用；而当空气弹簧处于拉伸状态时，承压平面半径R较小，此时气压力较小，材料特性对空气弹簧特性将产生较大的影响。

根据定义可知，囊体材料特性系数u的不同取值可以反映囊体材料的特性。由图5可知，同一工作压力下（0．5 MPa），u取值越大，空气弹簧载荷越大，尤其是拉伸状态下与忽略材料特性的模型差别也越大。

图5 材料特性系数对输出力的影响Fig．5 Influence of material properties coefficient on output force

3 实验验证

3．1 实验方案

为了测试空气弹簧在静态加载下的输出力，设计了实验台架，实验装置如图6所示。

图6 空气弹簧静态特性实验台架图Fig．6 Device for air spring static experiments

本实验采用Festo公司的EB－145－60型囊式空气弹簧作为研究对象。选定空气弹簧一系列工作高度依次进行实验。在选定的每一个工作高度下，进行静态加载，依次改变囊内气体工作压力，待囊内气压稳定后记录测得的输出力值。

3．2 实验结果分析

对空气弹簧的实验数据进行处理，并与仿真结果进行对比，可得到如下一些结果。

图7所示，空气弹簧有效作用面积随着工作高度变化而变化。如认为有效面积是接触面积或承压面积，则会出现不能接受的误差，所以这两种计算方法都是错误的；假设取空气弹簧高度为85 mm时的有效面积为恒定面积，当空气弹簧振幅为5 mm时就会产生最大高达12%的误差，由此可知有效面积恒定不变的假设必须在振幅很小的情况下才成立。

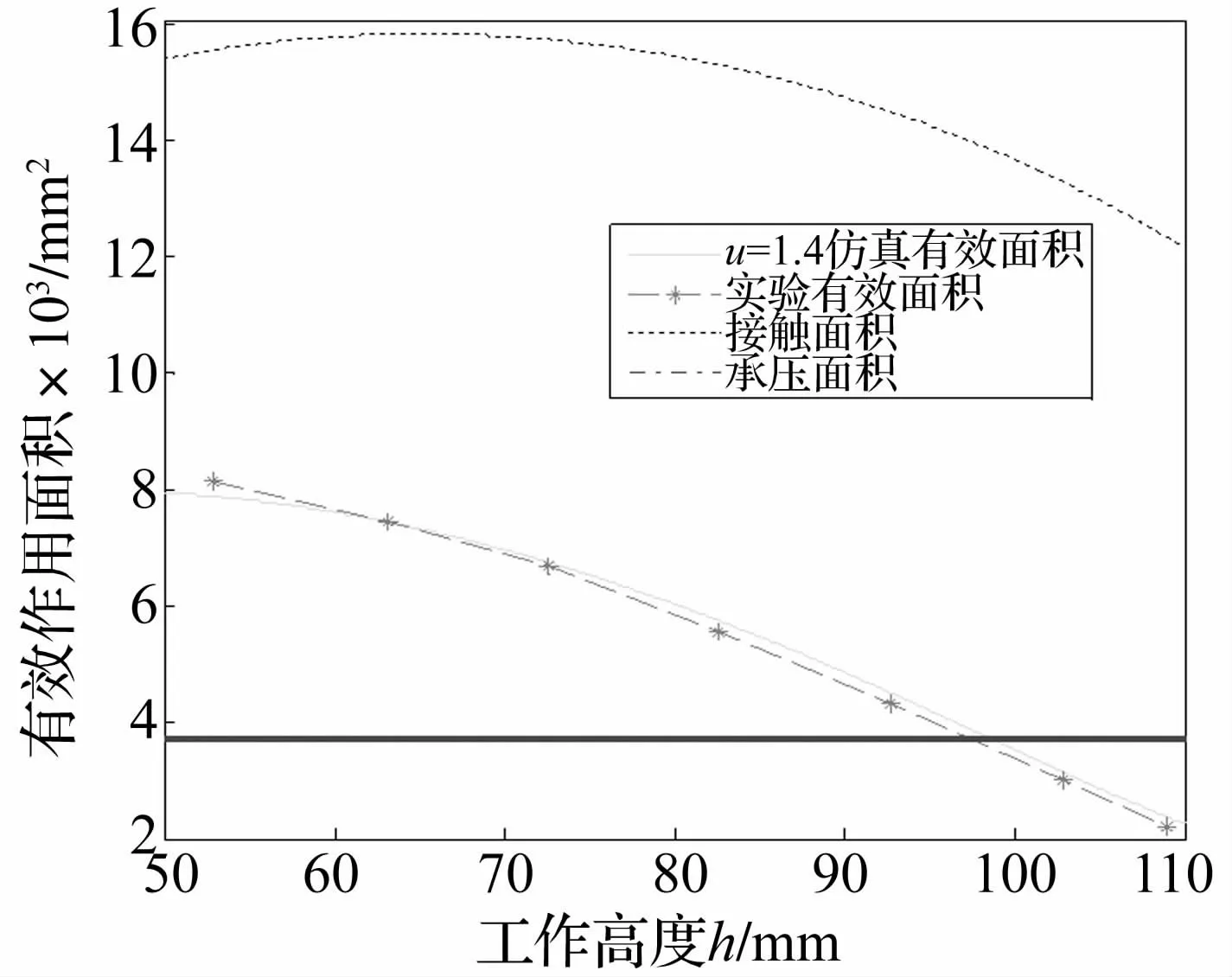
图7 有效面积和高度变化关系曲线Fig．7 Effective areas change with height

图8 仿真与实验数据对比Fig．8 Comparison between simulation and measurement

图8 是工作压力分别为 0．3 MPa、0．5 MPa、0．7 MPa时两种模型输出力仿真与实验对比曲线。从图中可以看出，忽略材料特性的模型（u＝1）与实验曲线在拉伸状态下差别较大，而基于囊体材料特性的模型（u＝1．4）与实验更加吻合，这说明载荷计算中考虑囊体材料特性因素很有必要。

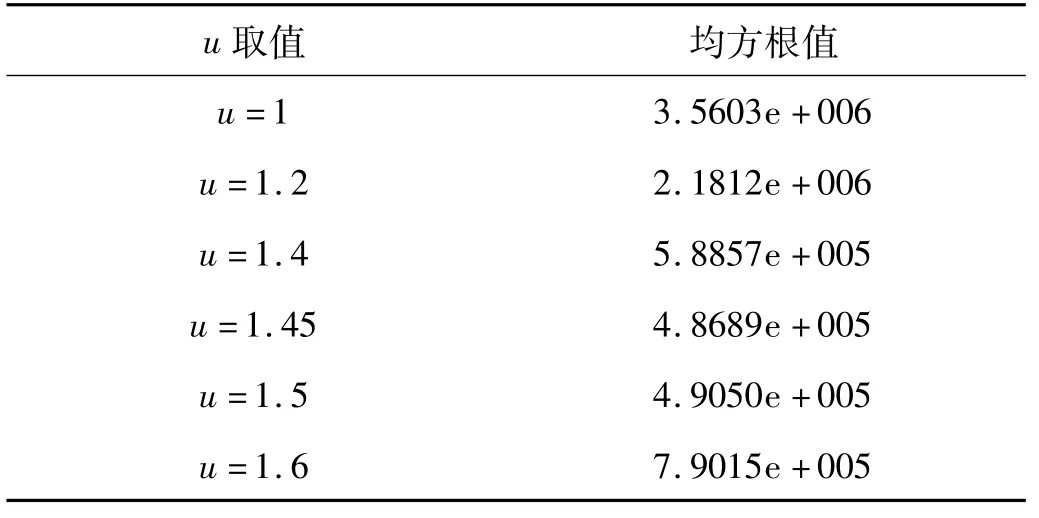
表1 仿真与实验误差平方和Tab．1 Simulations and measurement error sum of squares

分别计算囊体材料特性系数u取不同值时仿真计算值并与实验数据进行对比。对应不同u值仿真与实验的误差值平方和如表1所示。根据最小二乘法原理可得对于本实验采用的空气弹簧，在整个工作高度区间u取1．45时实验与仿真数据误差值平方和值最小，即模型与实际最接近。

3．3 误差原因分析

从图8中可以看到，模型在较低工作压力时拉伸状态下仍然与实验存在一定的误差。这很大程度上是由于实验数据的采集误差造成的。本实验中选用的力传感器的量程为20 kN，而低压拉伸状态下输出力小于2 kN，测量值处于传感器测量范围的前端10%内，此范围内采集误差对实验数据的影响比较大。

误差另一个主要的原因是模型推导中的假设条件。在强拉伸状态下，弧长不变的假设将导致仿真计算误差增大。

另外，其它一些因素也会对实验产生影响，包括橡胶的蠕变和橡胶滞后性能等［9－10］。实验过程中的对空气弹簧完成的拉伸压缩次数、空气弹簧实验中形变方向、充压保持时间等因素都会对囊体橡胶性能产生一定影响，进而影响到实验结果。

4 结 论

分析了囊体材料特性对空气弹簧特性的影响，并在此基础上建立了载荷模型，揭示了囊式空气弹簧承载和气压、几何参数之间的函数关系。虽然是基于几何图解的方法推导得到，但经实验验证该模型描述空气弹簧的载荷特性有较高的精确度。本文给出的计算表达式简单、准确、可应用性强，对于囊式空气弹簧分析计算具有重要的指导意义和实用价值。

［1］叶珍霞，朱海潮，鲁克明，等．囊式空气弹簧刚度特性的非线性有限元法研究［J］．振动与冲击，2006，25（4）：94－97．YE Zhen-xia，ZHU Hai-chao，LU Ke-ming，et al．Study on stiffness characteristics of air spring with nonlinear finite element method［J］．Journal of Vibration and Shock，2006，25（4）：94－97．

［2］张树桢，陈前，滕汉东．囊式混合介质隔振器的动力学特性试验［J］．振动与冲击，2012，31（11）：98－103．ZHANG Shu-zhen，CHEN Qian，TENG Han-dong．Tests for dynamic properties of a gasbag SALiM vibration isolator［J］．Journal of Vibration and Shock，2012，31（11）：98－103．

［3］楼京俊，朱石坚．长方体形空气弹簧刚度计算［J］．噪声与振动控制，2001，21（4）：22－26．LOU Jing-jun， ZHU Shi-jian． Stiffness calculation of rectangular air spring［J］．Noise and Vibration Control，2001，21（4）：22－26．

［4］佟雪峰，陈克，王新芳，等．囊式空气弹簧力学特性分析与研究［J］．沈阳理工大学学报，2011（5）：63－67．TONG Xue-feng，CHEN Ke，WANGXin-fang，et al．Analysis of the mechanical properties of air spring［J］．Journal of Shenyang Ligong University，2011（5）：63－67．

［5］王树林．关于空气弹簧的弹性特性及其在振动磨机上的应用［J］．西安建筑科技大学学报：自然科学版，1986（1）：1－8．WANG Shu-lin．Elastic characteristics of air spring and its application to vibration-grinder［J］．Journal of Xian Institute of Metallurgy and Construction Engineering：Engineering Science，1986（1）：1－8．

［6］郑明军，林逸，王海花，等．多曲囊式空气弹簧非线性弹性特性研究［J］．振动与冲击，2009，28（8）：11－15，29．ZHENG Ming-jun，LIN Yi，WANG Hai-hua，et al．Nonlinear stiffness characteristics ofmultilayer cystiform air spring［J］．Journal of Vibration and Shock，2009，28（8）：11－15，29．

［7］郭荣生．橡胶弹簧的特性计算［J］．铁道车辆，1978（10）：26－35．GUO Rong-sheng．Characteristic calculation of rubber spring［J］．Rolling Stock，1978（10）：26－35．

［8］夏仕朝．空气弹簧隔振系统载荷分配优化研究［D］．西安科技大学，2008．

［9］宋红光，于磊，刘志国，等．关于空气弹簧内部间隙的研究［J］．铁道车辆，2012（7）：1－5．SONG Hong-guang，YU Lei，LIU Zhi-guo，et al．Research on the clearances inside air springs［J］．Rolling stock，2012（7）：1－5．

［10］束立红，何琳．聚氨酯隔振器蠕变特性力学模型试验研究［J］．噪声与振动控制，2012，32（2）：147－150．SHU Li-hong， HE Lin．Mechanical model for creep performance testing and analysis of polyurethane Isolator［J］．Noise and Vibration Control，2012，32（2）：147－150．