基于构件的钢筋混凝土核心筒结构地震损伤分析
郑山锁,徐 强,杨 丰,孙龙飞,杨 威
(西安建筑科技大学 土木工程学院,西安 710055)
钢筋混凝土核心筒结构以其优良的抗震性能被广泛应用于实际工程,但目前对此类结构地震损伤模型的研究较少,针对结构整体损伤的研究主要有整体法和加权系数法两种,前者借助计算机软件进行数值模拟,将整体结构的位移、变形等地震响应特性作为分析目标,从宏观上把握结构的整体性能,但该方法忽略了局部构件损伤对整体结构损伤的影响;后者基于结构的层损伤确定各层的损伤指数,再按一定的权重系数进行加权组合,最终得到整体结构损伤指数,从而能较好地考虑局部结构损伤对整体结构损伤的影响。国内外基于加权系数法研究结构的损伤模型,基本都只是简单地考虑了不同结构层损伤对整体结构损伤的影响,并未深入的研究同一层中不同构件的损伤对层损伤的影响。
鉴于此,本文为实现构件(局部)损伤向结构(整体)损伤迁移转化的多尺度效应,基于对剪力墙及连梁构件地震损伤性能的研究,参考国内外RC核心筒抗震性能的研究成果(数值模拟方法及试验方法的结论和数据),建立了能够反映构件、楼层以及整体三者之间损伤迁移转化规律的RC核心筒结构地震损伤模型。结合试验结果,给出了RC核心筒的损伤状态及相应的损伤指数范围,并对损伤模型的有效性进行了验证。
1 RC核心筒构件损伤分析
1.1 构件损伤指数计算
国内外震害资料表明,整体结构的破坏均源于局部构件的损伤,对基本构件地震损伤性能的研究尤为重要。基于钢筋混凝土剪力墙地震损伤试验,按照双参数损伤模型计算剪力墙损伤指数[1],其表达式为:
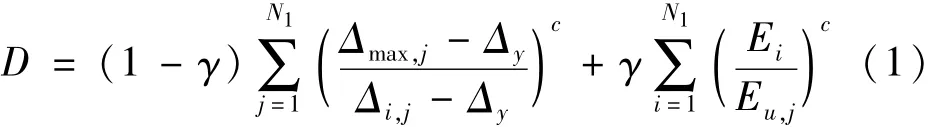
式中:Δy为屈服位移;Δmax,j为第 j次半循环所对应的最大非弹性变形;N1为第一次产生的最大非弹性变形Δmax,j的半循环次数;Δu,i为第 i次半循环加载后,再次单调加载时构件的极限变形能力;Ei为第i次半循环的滞回耗能;Nh为半循环次数;γ为组合参数;c为试验参数。Eu,i为经历i次半循环加载后,再次进行单调加载时构件的极限耗能能力,与构件经历的半循环加载次数有关。
连梁损伤指数可按照文献[2]方法进行计算,其表达式为:

其中:
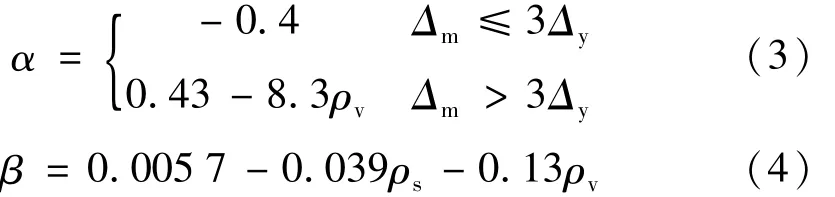
式中:Δy和Δm分别为构件的屈服位移和反复荷载作用下实际经历的最大位移,并且,当Δm≤Δy时,不考虑卸载刚度的退化;Fy为构件屈服荷载;Fm为对应于Δm处的荷载值;α为系数,其值越大,构件的刚度退化越不明显;β为与构件参数有关的强度衰减因子;Ei为第i个滞回环的耗能;ρv为构件的体积配箍率;ρs为构件配筋率。
1.2 构件损伤权重系数
构件损伤的权重系数 ηij,w和 ηkj,b表示本楼层内各个构件对楼层总体损伤的贡献大小。研究结果表明[2],随着构件滞回耗能的增大,其损伤累积不断加大,因此采用构件滞回耗能作为权重系数来反映不同构件损伤对所在结构层损伤的影响,单层各个构件损伤权重系数的计算式如下:
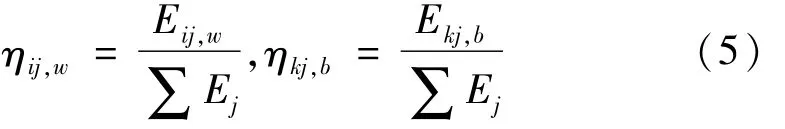
其中:
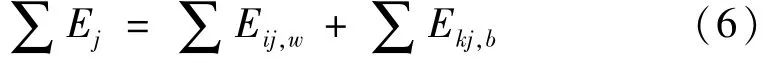
式中:∑Ej为第 j层总的滞回耗能;∑Eij,w、∑Ekj,b分别为第j层剪力墙总滞回耗能以及第j层连梁总滞回耗能。
1.3 构件-层的损伤迁移规律
本文参考文献[3]试验,对RC核心筒结构进行数值模拟,分别计算出各层墙、连梁的损伤值,赋予其相应的权重系数得到各层剪力墙的总体损伤贡献值和连梁的总体损伤贡献值,将墙、连梁损伤贡献值组合得到结构单层的损伤值。分别以结构单层总体损伤值、墙和连梁损伤贡献值为纵坐标,以往复荷载循环次数为横坐标,绘制出结构各层损伤值、墙和连梁的损伤贡献值与往复荷载循环次数之间的变化关系如图1所示。
分析图1能够得出以下两个结论:
(1)剪力墙对整个结构层的损伤贡献大于连梁对整个结构层的损伤贡献。对于结构的某一层而言,墙体对结构层的损伤贡献约为55%,连梁对结构层的损伤贡献约为45%,此比率在循环初期基本保持稳定,随着循环次数的增加,二者的损伤值同时增大,连梁达到破坏首先退出工作,墙体达到屈服以后损伤值不断增大,对层损伤贡献的比例逐渐加大,截至破坏时,墙体对结构层的损伤贡献达到60%左右。
(2)同一位移幅值循环荷载作用时,结构层的损伤值有所增加,说明提出的层损伤模型可以较好地体现滞回耗能累积效应对结构层损伤的影响。
2 RC核心筒结构层损伤分析
2.1 RC核心筒结构层损伤模型
基于构件的地震损伤分析,以结构中各子结构或构件的损伤性能为出发点,分别赋予其相应的权重系数来进行叠加,最终得到结构的层损伤指数,层损伤指数函数如下式:
式中:D为整体结构层的损伤指数;D1、D2、D3、Dm分别为各个层局部单元的损伤指数。
RC核心筒结构楼层的损伤应该同时考虑剪力墙损伤和连梁损伤两个方面[3],故基于核心筒结构墙体、连梁的损伤模型,根据数值模拟的分析结果,赋予其相应的权重系数并进行组合,进而得到结构层损伤模型,实现损伤由构件向楼层迁移转化的研究目标。核心筒单层计算简图如图2所示。
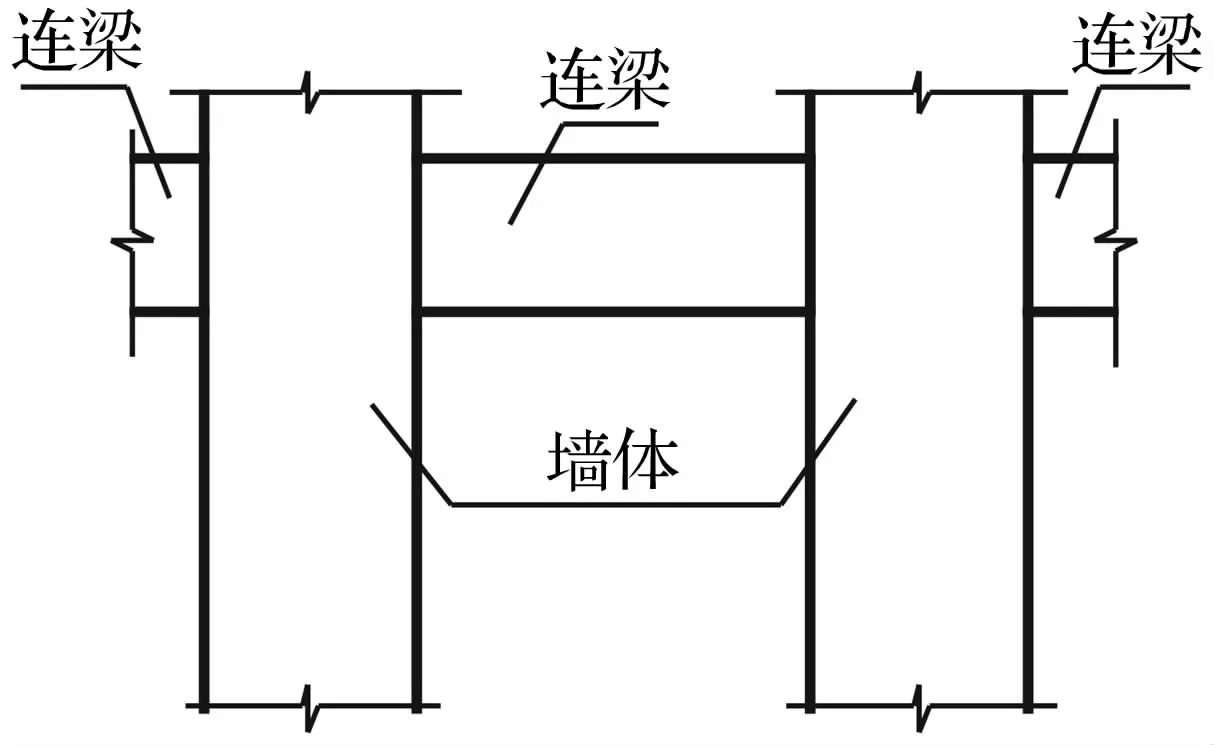
图2 单层计算简图Fig.2 Calculation scheme of single layer
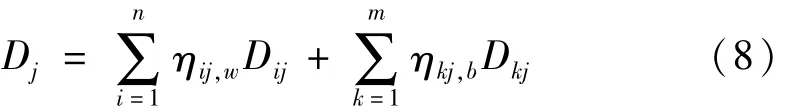
本文RC核心筒的层损伤模型定义如下式:
式中:Dj为第 j层损伤值;ηij,w为第 j层第 i片墙所对应的权重系数;n为筒体结构中第j层墙体总数;Dij为第j层第i片墙的损伤值;ηkj,b为第j层第 k根连梁所对应的权重系数;Dkj为第j层第k根连梁的损伤值。
2.2 结构层损伤权重系数的确定
已有的关于层损伤权重系数的选取和确定方法主要有以下几种:
Park等[4]定义层滞回能作为层权重系数;Chung等[5]引入层位置作为权重系数来反映不同层损伤对整体结构损伤的影响;欧进萍等[6-7]同时考虑了层位置和层损伤对整体结构损伤的影响定义层权重系数;杨栋等[8]认为上述两种确定层权重系数的方法对于刚度和层间位移较均匀的结构较为适用,而对非均匀结构,计算结果有失于偏颇,因此,提出采用楼层屈服强度系数作为层权重系数对整体结构进行损伤分析;Moham-mad等[9]认为上述定义反映了层到整体结构的损伤关系,但无法反映局部构件损伤对整体结构损伤的影响。另有学者从结构单层自重以及楼层屈服强度系数等角度出发来定义结构层损伤权重系数,均在一定意义上反映了结构层的损伤程度。
综合上述理论,本文以构件滞回耗能作为权重系数,建立了RC核心筒考虑局部构件损伤对整体结构损伤影响的整体结构损伤模型,其表达式为
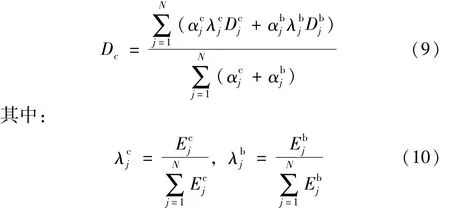
式中:N为结构层数;、分别为第j层剪力墙和连梁的校准系数;、分别为第j层所有剪力墙和连梁的滞回耗能;、分别为第j层剪力墙和连梁的权重系数;、分别为第j层剪力墙和连梁的总损伤指数,按下式计算[9]:
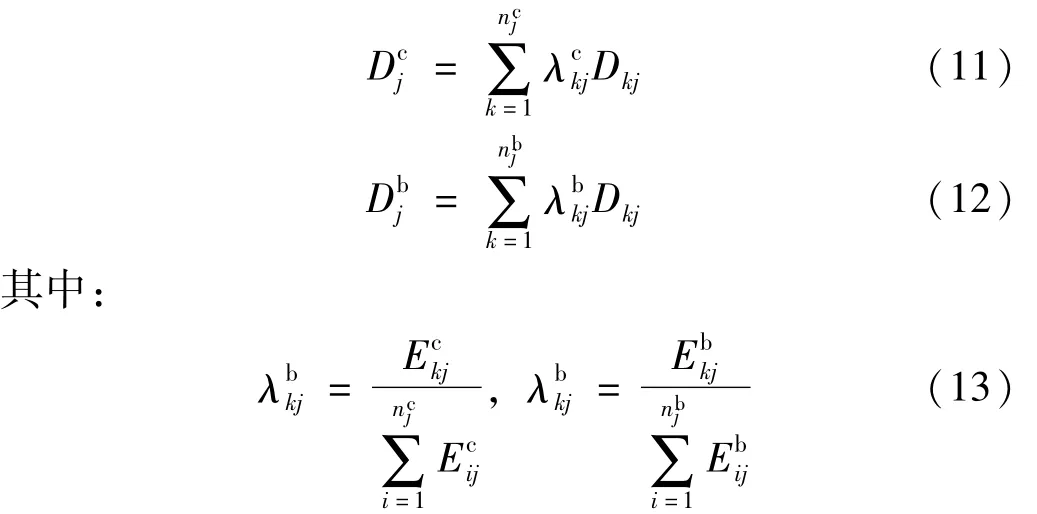
式中:、分别为第j层第k片剪力墙和连梁的损伤指数;、分别为第j层剪力墙和连梁数;、分别为第j层第k片剪力墙和连梁的权重系数;、分别为第j层第i片剪力墙和连梁的滞回耗能。
2.3 损伤权重系数参数的确定
结构层损伤权重系数λj的确定,关键在于其能够准确反映结构各层损伤对整体结构损伤的贡献。现有的研究成果一般只考虑单个因素的作用来确定λj,虽计算简单,但不能同时考虑各因素共同的影响。因此,赋予结构层不同的位置权重系数及损伤权重系数,合理地考虑结构层损伤和层位置对结构各层地震反应的影响:
(1)层位置权重系数γj的计算
杜修力等[10]提出的线性变化的位置权重系数适用于刚度和屈服强度分布比较均匀的框架结构,在结构底层较为符合,但是随着层数的增加,权重系数的退化较缓,这样考虑夸大了上部各结构层的重要程度,造成最终分析结果的不合理。
Chung等[5]提出的非线性变化的位置权重系数合理表述了结构上部各层的重要程度,但在结构底部各层退化较快,过度夸大了结构底层的重要性,而缩小了上部结构层对整个结构损伤的影响,当结构底层破坏时,整体结构已经破坏。底层的损伤值为1,而上部各层的损伤值可能很小,因而整体结构的损伤加权平均值可能小于1,易出现结构已破坏而整体结构的损伤加权平均值较小的不合理现象。
综上分析,针对两种系数的缺陷,本文提出一种介于二者之间的位置权重系数,表达式如下:

令N=20时,绘制出三种方法确定的结构层位置权重系数随着结构层数变化关系,如图3所示。
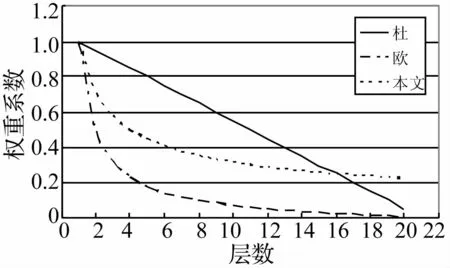
图3 结构层位置权重系数与结构层数的关系Fig.3 Relation of layer location weight coefficient and layer numbers
上图表明,本文提出的位置权重系数退化速率基本介于已有的两种系数退化速率之间,此退化规律即保留了两种系数退化规律的优点,又较好地体现了上部各层结构的重要程度,准确地表达了结构底部各层均有可能成为结构薄弱层的事实。
(2)层损伤权重系数μDj的计算
结构层损伤权重系数μDj能够直观地描述结构中单层较其他层的损伤程度,能反映本层结构损伤对整体结构损伤贡献,表达式如下:式中:Dj为结构第j层损伤指数。

2.4 层损伤权重系数的确定
本文采用位置权重系数与结构单层损伤权重系数二者组合的形式来确定层损伤权重系数,其具体表达式如下:

式中:γj为第j层位置权重系数;μDj为结构第j层损伤权重系数。
将计算结果与根据试验结果所确定的整体结构损伤指数变化关系进行对比,如图4所示。
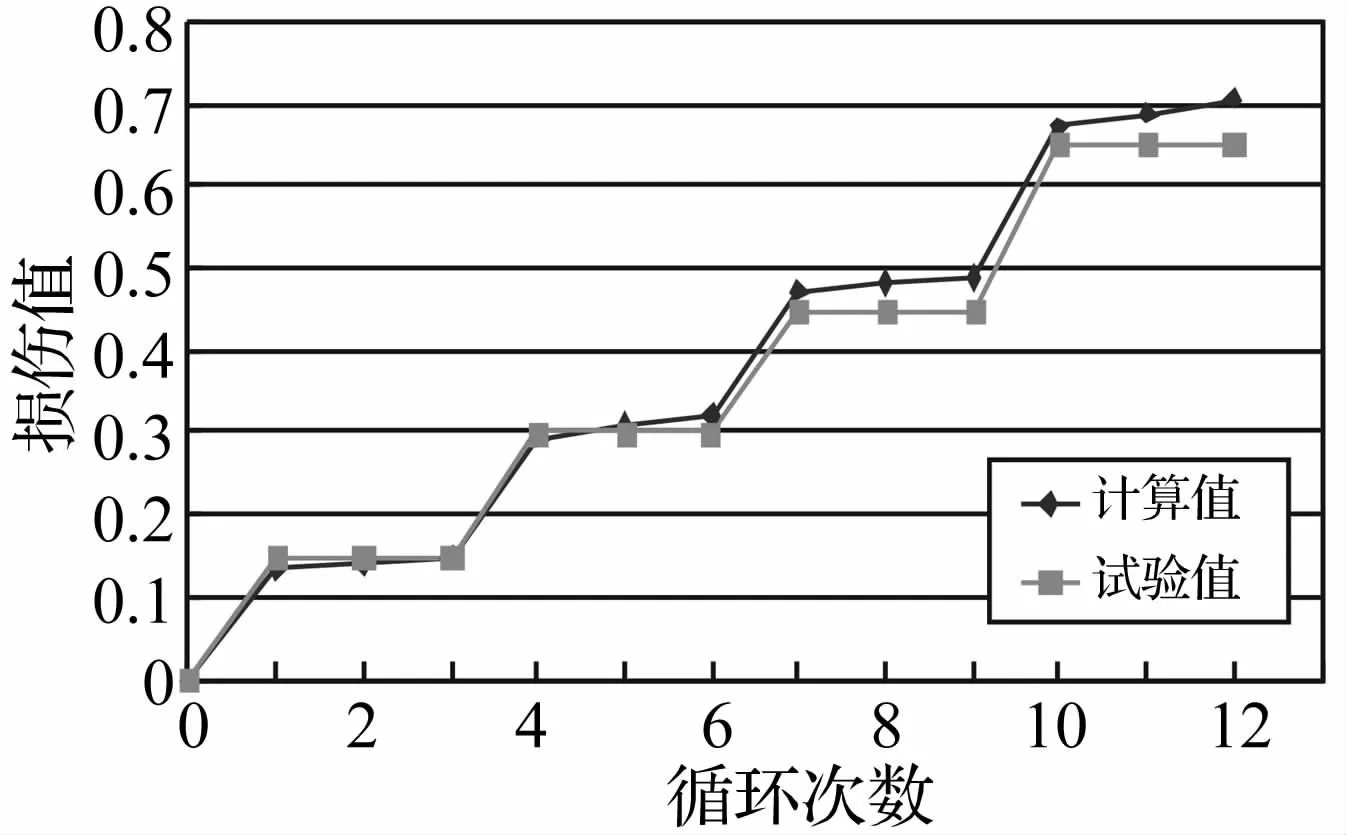
图4 损伤计算值与试验值的对比Fig.4 Comparison of calculation and test results
由上图可以看出,计算得到的理论损伤值与试验值吻合较好,表明位置权重系数与结构单层损伤指数组合的结构层损伤权重系数可以较为准确地描述RC核心筒结构的破坏过程,较好地反映结构的破坏特性。
3 RC核心筒结构整体损伤分析
3.1 结构整体损伤模型
基于加权系数法的整体结构损伤模型如下:

式中:λj为第j层损伤权重系数;Dj为第j层损伤指数;N为结构总层数。
综上述理论,本文最终确定出RC核心筒结构地震损伤模型的表达式为:

式中:γj为第j层位置权重系数;μDj为结构第j层损伤权重系数;Dj为结构第j层损伤指数。
3.2 RC核心筒结构损伤状态及相应损伤指数
在对震后建筑结构的损伤程度以及经济损失评估时,Kunnath等[4]将结构损伤程度分为:无损、轻微损伤、中度损伤、重度损伤以及倒塌五个等级;Bracci等[11]将结构损伤程度分为:无损、轻微损伤、可修复、不可修复和倒塌等状态。本文基于上述理论,结合相关收集资料,给出了RC核心筒结构的性能水准及宏观描述见表1;RC核心筒的破坏程度及相应的损伤指数范围见表2。
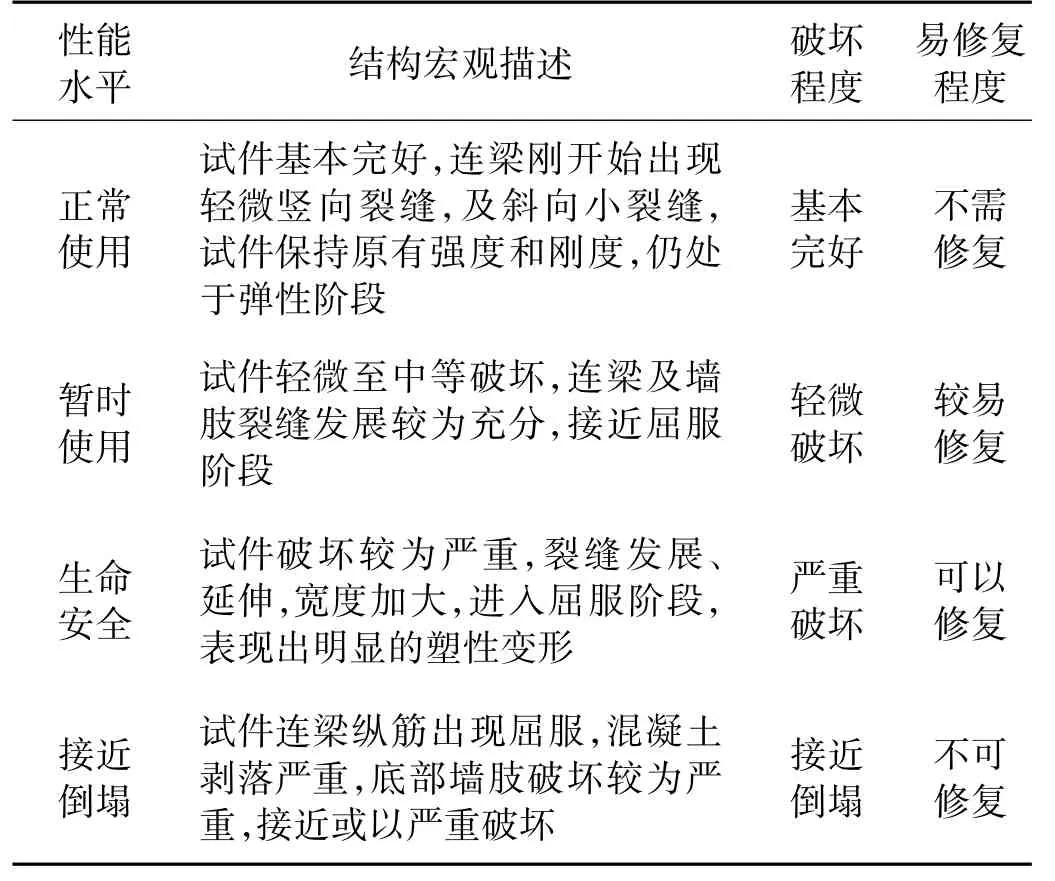
表1 RC核心筒结构性能水平及宏观描述Tab.1 Performance Level of RC Core Walls Structure

表2 RC核心筒结构的破坏程度及相应损伤指数Tab.2 Damage states and corresponding damage indexes of RC core walls structure
3.3 基于结构整体损伤模型分析验证
本文按照反应谱特征周期与设计场地特征周期相近的原则选取地震波,选取15条地震波记录见表3所示。基于传统的增量动力分析(IDA)方法,同时考虑地震动强度和地震动入射角,对结构进行多元增量动力分析(MIDA),对所得的整体损伤模型的有效性进行验证分析。
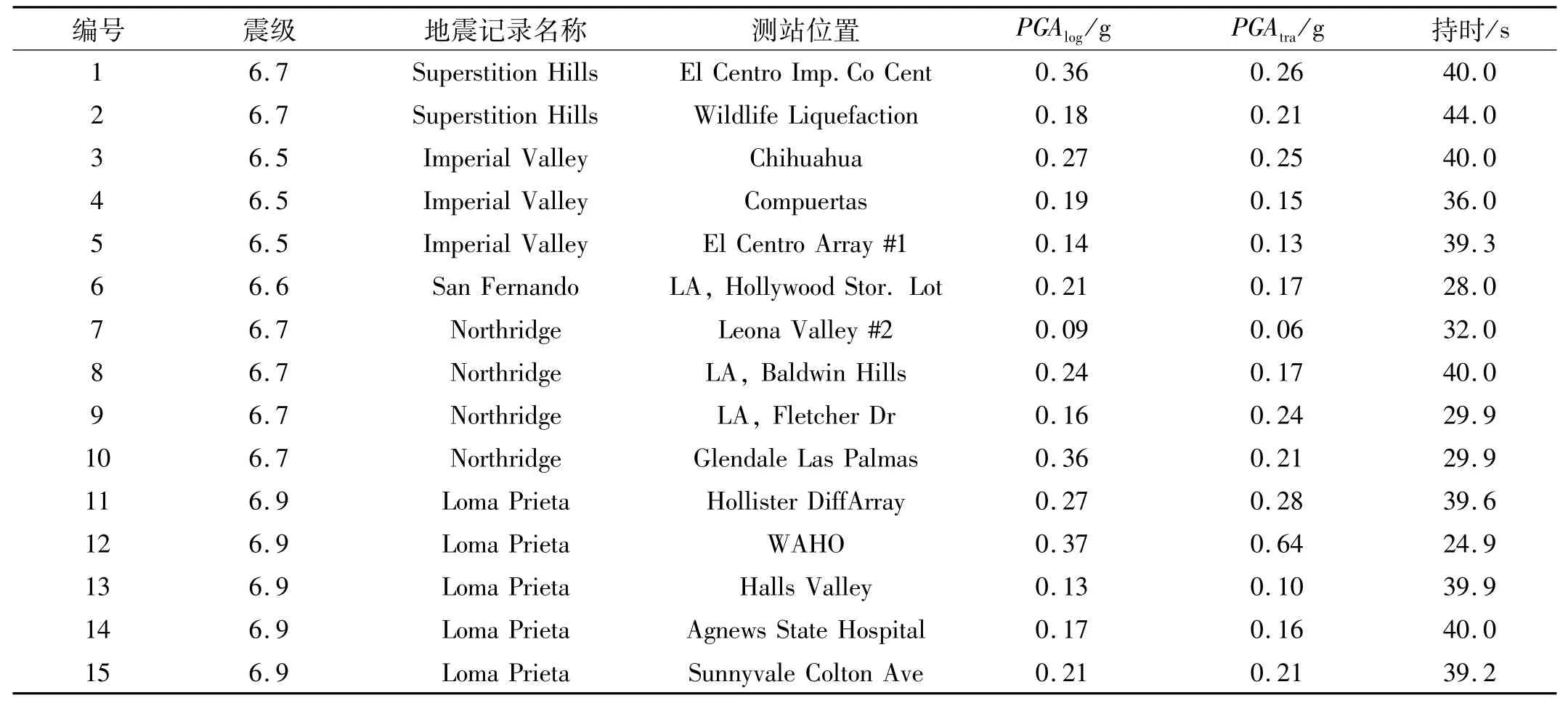
表3 文中选用的地震动记录Tab.3 Seismic Records in this Paper
一系列地震动记录和地震入射角(0°~180°)都是独立同分布的随机变量,基于拉丁超立方体网络抽样方法[12]确定地震动记录和地震动入射角,如图5所示。
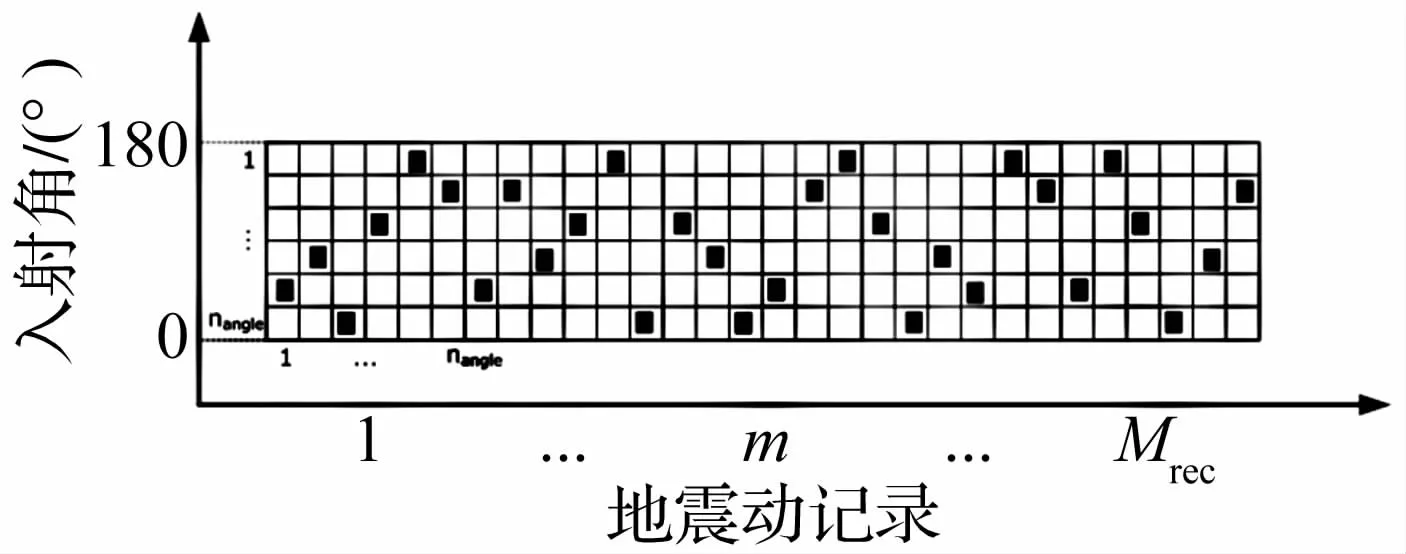
图5 地震动记录-入射角的拉丁超立方网络抽样分布Fig.5 Latin hypercube sampling of record-incident angle pairs
地震入射角的数量与所选取的地震动记录满足如下关系:

式中:nangle为选取的地震动入射角数量;Mred为选取地震动记录的数量;Nsic为表征地震动记录-地震入射角的“地震对”,分布在1°~180°范围内的地震入射角决定了“地震对”的数量选取。
基于考虑地震动强度和入射角等随机因素,选用结构的最大地震动损伤指数Dmax作为结构地震动响应(DM)指标,本文对Dmax的定义式如下:

式中:D(t)x、D(t)y分别代表沿结构 x、y方向随时间变化的最大损伤值。
采用拉丁超立方体网络抽样法随机选取3条典型的地震波记录及相应的5个地震动入射角,对Sa(T1,5%)其进行调幅,使得强度覆盖结构从弹性阶段、弹塑性阶段直至倒塌各个阶段可能遭受到的地震动范围,将调幅后的地震动记录按选取的地震动入射角依次进行对结构进行多元增量动力时程分析(MI-DA),得到每一次调幅后结构的最大损伤值Dmax直至其趋近于1,即结构发生倒塌破坏,此时停止分析。将分析所得的有效(Dmax,Sa)点绘制于DM-IM坐标系中,得到相应的MIDA曲线如图6所示。
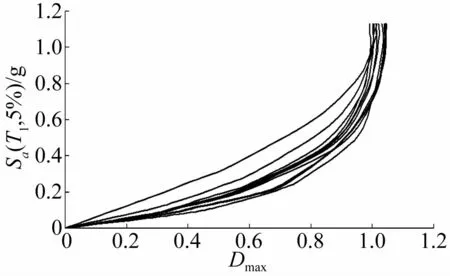
图6 数值模拟所得MIDA曲线Fig.6 MIDA Curves obtained from numerical simulation
MIDA曲线与地震记录与地震入射角的选取相关,地震记录和入射角的随机性造成了MIDA曲线的差异性。因此,本文采用混合统计方法来降低这种差异性。在下限MIDA曲线相应的强度 Sa(T1,5%)等级范围内,按IM方法进行统计;在上、下限MIDA曲线水平段部分相应的强度等级Sa(T1,5%)范围内,按DM方法统计分析,分别得到得50%、16%和84%分位数曲线如图7所示。
从图7可看出,曲线在Sa处于0~0.18g左右范围内基本是一条直线,即结构变形在弹性范围内;其后结构达到屈服,随着塑性的逐步发展,在Sa处于0.32~0.57g左右范围内,曲线斜率有一段相对上升的阶段,出现所谓的应力硬化现象;直至当Sa≈0.76g时,结构损伤趋近于1。此后随着Sa的轻微增加,Dmax将不再增长,结构体系已经达到整体动力失稳状态。3条不同分位曲线上四个性能点对应的损伤值Dmax和Sa(T1,5%)如表4所示。
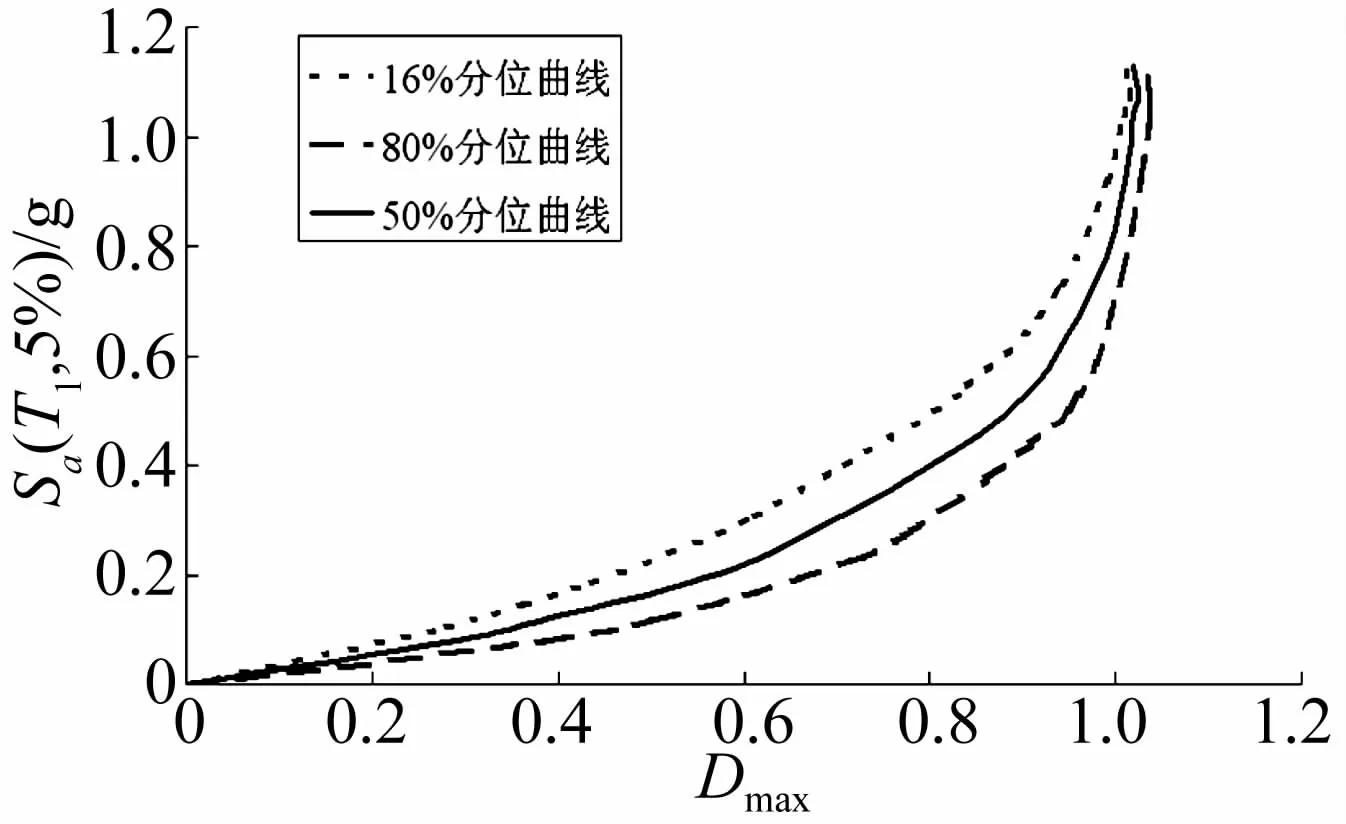
图7 统计16%、50% 、84%MIDA曲线Fig.7 16%,50%and 84%Statistics MIDA curves
由3条分位线上各性能点对应的损伤均值可得到结构正常使用、暂时使用、生命安全和接近倒塌性能状态的最大损伤限值。当最大损伤限值达到0.32时,结构基本处于弹性状态,建筑各项功能均可正常使用;当最大损伤限值达到0.47时,结构发生轻度破坏,经修理后仍可继续使用;当最大损伤限值限值达到0.68时,结构保持稳定状态,可保证生命安全的目标;当最大损伤限值达到0.94时,大部分连梁发生破坏,底部剪力墙也发生一定损坏,核心筒主体结构倒塌的几率增大。

表4 16%,50%和84%MIDA曲线的各性能点Tab.4 Performance points of 16%,50%and 84%MIDA curves
将结构相应各损伤状态下的最大层间位移角与已有试验数据[3]进行对比见表5所示。结果表明,本文所定义钢筋混凝土核心筒结构的性态点是合理的。

表5 MIDA方法与试验方法性能指标限值的对比Tab.5 Comparion of performance iindex limit value by MIDA and test
将分析结果与表2中结构的破坏程度及相应损伤指数进行对比,结果表明,本文提出的整体损伤模型是合理有效的。
4 结 论
本文基于构件的损伤,建立了RC核心筒结构地震损伤模型,主要结论如下:
(1)采用加权系数法建立的RC核心筒地震损伤模型,概念清晰,物理意义明确。该模型考虑了构件损伤对整体结构损伤的影响,能够对结构层次上损伤发展的演化行为进行较为准确的把握与描述。
(2)与筒体结构物理试验结果对比表明,本文所建立的整体损伤模型能够较好地反映RC核心筒结构的损伤发展过程。该模型可为地震作用下该类结构的损伤评估以及基于损伤的抗震设计方法的建立提供参考。
(3)给出的RC核心筒结构地震破坏程度及相应的损伤指数范围,基于多元增量动力分析对本文提出的损伤模型的有效性的进行了验证,为该类结构震后损伤评估提供了理论依据。
[1]王斌,郑山锁,国贤发.型钢高强高性能混凝土框架柱地震损伤分析[J].工程力学,2012,29(2):61-68.WANG Bin, ZHENG Shan-suo, GUO Xian-fa. Seismic damage analysis for srhshpc frame columns[J].Engineering Mechanics,2012,29(2):61-68.
[2]于飞.型钢高强高性能混凝土框架梁损伤试验及损伤分析[D].西安:西安建筑科技大学,2010.
[3]侯炜.钢筋混凝土核心筒抗震性能及其设计理论研究[D].西安:西安建筑科技大学,2010.
[4]Kunnath S,Reinhorn A,Park Y.Analytical modeling of inelastic seismic response of RC structures[J].Journal of Structural Engineering,1990,116(4):996-1017.
[5]Chung Y S,Meyer C,Shinozwha M.Modeling of concrete damage[J].Struct.ACI,1989,86(3):259-270.
[6]欧进萍,何政,吴斌,等.钢筋混凝土结构基于地震损伤性能的设计[J].地震工程与工程振动,1999,19(1):21-29.OU Jin-ping,HE Zheng,WU Bin,et al.Design of reinforced concrete structure based on seismic damage performance[J].Earthquake Engineering and Engineering Vibration,1999,19(1):21-29.
[7]李洪泉,欧进萍.剪切型钢筋混凝土结构的地震损伤识别方法[J].哈尔滨建筑大学学报,1996,29(2):8-12.LI Hong-quan,OU Jin-ping.An identification method of shear-type RC frame for earthquake damage[J].Journal of Harbin University of Civil Engineering and Architecture,1996,29(2):8-12.
[8]杨栋,丁大钧,宰金?.钢筋混凝土框架结构的地震损伤分析[J].南京建筑工程学院学报,1995,4:8-13.YANG Dong,DING Da-jun,ZAI Jin-min.Seismic damage analysis of reinforced concrete frame structures[J].Journal of Nanjing Collage of Civil Engineering and Architecture,1995,4:8-13.
[9]Mohammad R, Ali Bakhshi. Vulnerability and damage analyses of existing buildings[J].13th World Conference on Earthquake Engineering,Canada,2004:1-13.
[10]杜修力,欧进萍.建筑结构地震破坏评估模型[J].世界地震工程,1991,7(3):52-58.DU Xiu-li,OU Jin-ping.Seismic damage evaluation model of building structures[J].World Earthquake Engineering,1991,7(3):52-58.
[11]Bracci J M, Kunnath S K, Reinhorn A M. Seismic performance and retrofit evaluation of reinforced concrete structures[J].Journal of Structural Engineering,1997,123(1):3-10.
[12]McKay M D,Beckman R J,Conover W J.A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J].Technometrics,1979,21(2):239-245.

