分裂导线次档距振荡研究

李 黎，王腾飞，陈元坤

（1．华中科技大学 土木工程与力学学院，武汉 430074；2华中科技大学 控制结构湖北省重点实验室，武汉 430074；3．中南建筑设计院股份有限公司，武汉 430071）

次档距振荡是一种由迎风侧子导线的尾流诱发背风侧子导线振动的现象，是分裂导线的特有振动现象，它属于气动不稳定引起的振动。次档距振荡的振动频率约为1～3 Hz，振幅为0．1～0．5 m，振动轨迹呈水平扁长椭圆，会造成子导线间的相互碰撞和鞭击，磨损导线，且较大的振幅也使间隔棒线夹处导线的动弯应变增大，导致导线疲劳断股。次档距振荡涉及到复杂的流固耦合和空气动力学问题。加上子导线和间隔棒之间的相互作用，使得该问题的研究难度比较大。Simp-son［1－2］与 Cooper［3－4］利用准定常线性驰振理论，预测特定条件下驰振发生的边界条件，并在试验条件下证明这些不稳定。Tsui等［5－6］利用准定常理论研究了亚临界与超临界流体范围内处在固定导线尾流中的背风面子导线的二维驰振稳定问题。Price［7］同时利用准定常线性驰振理论与无阻尼理论分析尾流驰振发生的条件，结果表明两种理论都证明背风面导线的固有频率对尾流驰振的发生十分重要，并通过试验结果证明了该结论。叶志雄［8］给出了控制次档距振荡的阻尼间隔棒最大安装距离的计算方法。冯学斌［9］对多分裂导线次档距的优化布置进行了研究。相对来说，国内对分裂导线的次档距研究不够深入，集中于对次档距振荡控制的研究，缺少计算分裂导线次档距振荡成熟的数学模型与理论分析，因此有必要对分裂导线的尾流驰振机理进行深入研究。本文将在 Simpson［10］、Tsui等［5］研究的基础上基于准定常理论建立分裂导线次档距振荡的二自由度振子模型振动方程，利用稳定性理论对振子模型初始平衡位置的进行分析，得到次档距振荡发生的临界条件，并研究了其参数敏感性，对次档距振荡的控制给出了建议。

1 次档距振荡的模型

研究表明上游迎风侧子导线的运动对下游子导线的运动影响很小，可假定上游子导线为固定静止状态［11］，重点研究其尾流中背风下游子导线的驰振现象。大量研究表明二维模型能反映尾流驰振的基本现象，其计算简图如图1所示。

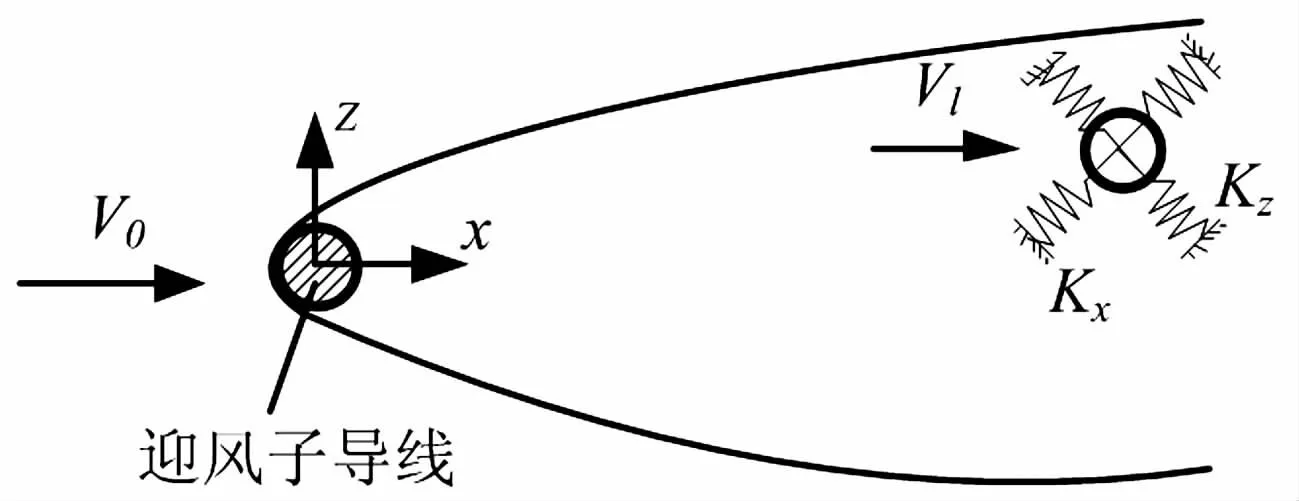
图1 背风导线二维振子模型Fig．1 Two-dimensional oscillator model of the leeward wire

振子模型的非线性主要局限于气动力模型，结构模型是线性。为方便建立数学模型，作用在下游子导线上的气动力为F，假设下游子导线的质量为m，直径为d，只考虑尾流中下游子导线的平面运动，且其支撑于正交的弹簧阻尼系统，x与z向的刚度分别为Kx、Kz，且其倾角为φ。阻尼比分别为ζx、ζz。沿x与z向的谐振频率分别为fx、fz。令其在平衡位置的坐标为（x0，z0），受扰动后新的位置为（x0＋x，z0＋z）。

根据牛顿第二定律，可建立尾流中下游背风侧子导线的振动方程为：

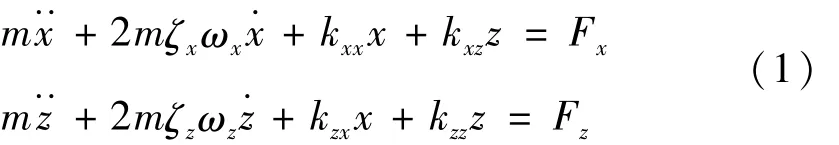
式中：Fx，Fz分别是作用在尾流中下游子导线的气动升阻力在两个主轴方向的分力，kxx，kzz是导线单位长度的轴向刚度，其与正交弹性支撑系统的刚度Kx、Kz存在如下关系：

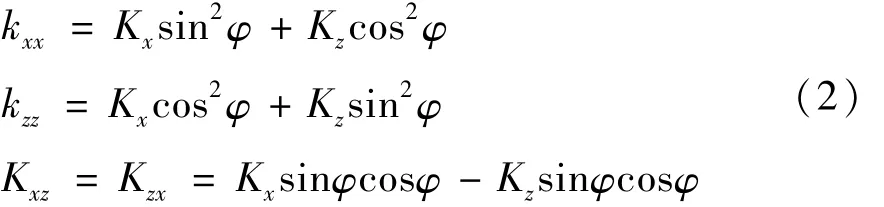
大量研究表明，尾流驰振是由描述平均的气动力现象的参数所决定的，而这些参数可以在物体固定不动时测得［12］。当圆柱处于另一圆柱的尾流中时，考虑尾流的屏蔽效应后，作用到其上的来流速度Vl不同于自由均匀来流速度V0，为简化分析，尾流速度Vl的方向假定为与V0一致。下游子导线相对于尾流速度Vl的气动力系数分别为槇CL、槇CD和槇Cm，由于导线是圆截面，不考虑扭矩系数。而相对于自由均匀来流的气动力系数可分别表示为CL、CD。其关系如式（3）所示：

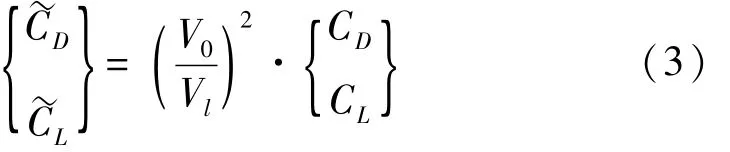
尾流中的速度Vl可表达成式（4）：

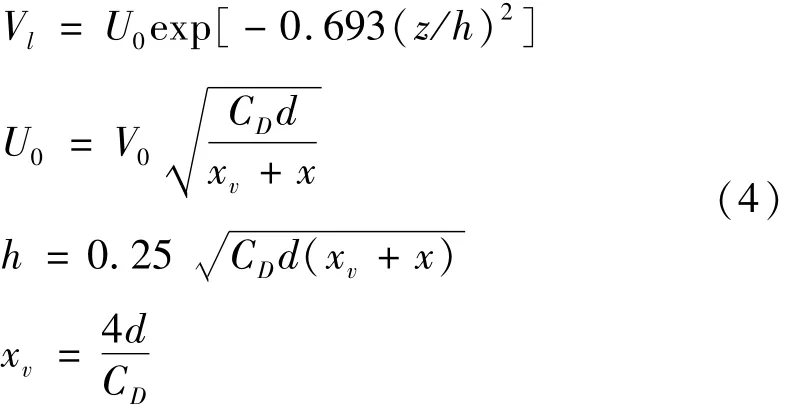
但若下游子导线在自由来流下的阻力系数为CD∞，Vl则可近似表示为：

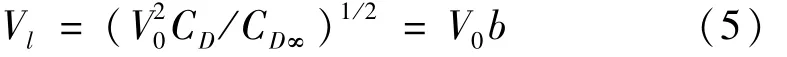
式中：b＝（CD／CD∞）1／2，且通常取 CD∞＝1．2。

下游子导线支撑于两正交且平行于主轴的弹簧阻尼系统。在这种情形下，子导线可以在平衡位置振动。则作用在尾流中的背风子导线的气动力可表示为：

式中：ρ为空气密度，取值为 1．22 kg／m3。

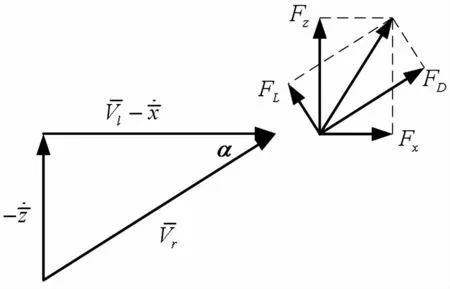
图2 气动力与速度矢量分解图Fig．2 Resolved components of aerodynamic and velocity vector

参考图2可知，两轴向分力Fx、Fz与气动升阻力有如下关系：

式中：α为尾流速度与y轴所成的角度，且其满足如下关系：

综合式（3）～式（8）可得到作用在尾流中下游子导线的气动力，并代入到振动方程（1）中可得到二自由度振子模型完整的振动方程为：

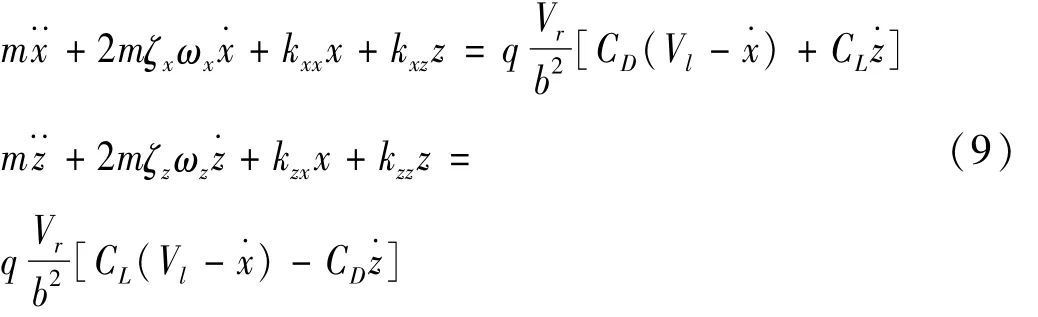
式中：q＝1／2ρd为气压，气动升阻力系数 CL与 CD是尾流中相对位置的函数。本文利用上节中通过CFD仿真并利用多项式拟合得到的表达式进行后续分析。下节中将讨论该振动方程组的稳定性问题以研究尾流中的背风侧子导线发生次档距振荡的临界条件。

2 次档距振荡稳定性分析

本节从稳定性理论出发揭示分裂导线的次档距振荡的机理。而稳定性分析方法归结为对振动微分方程的初值稳定性问题，通过临界状态计算确定次档距振荡发生的临界风速。首先将非线性振动微分方程线性化，根据系统的特征值分析来判断系统的稳定性。若系统的特征根均为负实数或具有负实部的共轭复数则系统初值稳定，否则系统不稳定。对于直接求解特征值工作量很大的系统，通常采用代数判据来判断系统的稳定性，常用的判据有：Routh稳定判据与Nyquist稳定判据。本文将采用Routh稳定判据，其本质是通过系统特征方程的各项系数进行代数运算，得出全部根具有负实部的条件，从而判别系统的稳定性，是一种时域判据，其计算过程简单，应用广泛。

为简化稳定性分析，假定背风子导线的初始平衡位置为（x0，z0），只考虑子导线围绕平衡位置的小幅振动，且将非线性气动力线性化。将非线性气动力表达式通过泰勒公式在初始平衡位置为（x0，z0）处展开可得：

式中：CD0与CL0是平衡位置处的气动力系数CD（x0，z0）与 CL（x0，z0）的简写。

尾流的相对速度Vr平方形式可表示为：

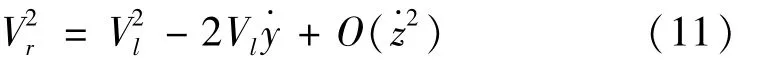
由于x与z相对较小，因此倾角α较小，可得到：

并引入无量纲坐标X＝x／d与Z＝z／d，定义无量纲导数，同样 C、C、C有类似的表DzLxLz达式，且忽略高阶项。

令＝X－X0，＝Z－Z0，并将上述线性化的气动力代入到振动方程（9）中，可得到最终的线性化的振动方程为：

合并与及它们的导数，用矩阵形式表达可得到下式：

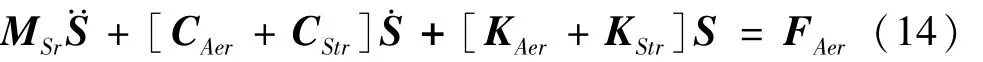
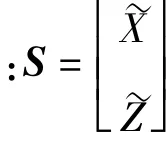
式中为无量纲位移向量；质量矩阵MSTR；结构刚度矩阵为；气动刚度矩阵为；结构的阻尼矩阵为；气动阻尼矩阵为，平衡位置处的气动力为 F＝Aer

为研究系统的稳定性，假定方程（13）解的形式为：

将上式代入到振动方程中可得到线性齐次方程为：

式中，Ur为缩减速度。

上述方程有非零解的必要条件是其系数行列式D＝0，从而可得到关于λ的特征方程为：

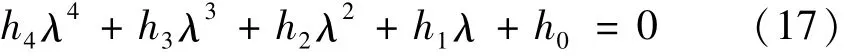
其中多项式的系数表达式如下：

系统的特征方程为四次方程式，可根据劳斯（Routh）判据进行稳定分析，为保证下游子导线处于稳定状态，必须满足如下不等式：

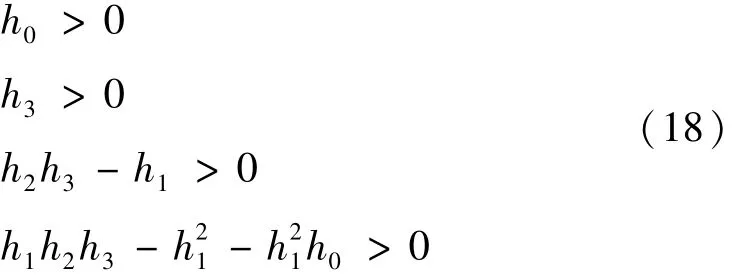
上述各项计算利用MATLAB编程来完成，根据各实际参数，计算出h0～h4，并按Routh判据作出稳定性判断，根据系统的稳定临界条件可求得分裂导线发生次档距振荡的临界风速。

当导线系统不稳定时，其有两种可能导致子导线会偏离平衡位置，即当h0＝0时，系统发生静态分岔；当h1h2h3－－h0＝0或h3＝0或h2h3－h1＝0时，系统发生Hopf动态分岔。静态分岔是针对平衡点的分岔问题；而Hopf动态分岔指参数变化且经过分岔值时，从平衡状态产生的孤立的周期运动的现象，也即从中心型平衡点产生的极限环的现象。为简化稳定性分析，在下文分析中假定正交弹簧的倾角φ＝0；且忽略系统的阻尼作用。

2．1 Hopf动态分岔

由于下游子导线的平均阻力系数CD＞0，则h3恒大于零。对于导线次档距振荡问题，h2h3－h1也总大于零。因此发生Hopf动态分岔的临界条件是：

将各参数代入，式（19）可以写成以下形式：

式中：

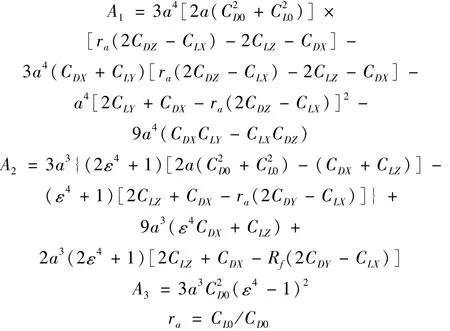
当缩减速度Ur存在正实根时，就会发生Hopf动态分岔。在此条件下，下游子导线将偏离其平衡位置而处于不稳定状态，即导线系统发生次档距振荡。方程（20）中Ur有正实根必须满足如下条件：

将 A1、A2、A3代入上式中，可得：

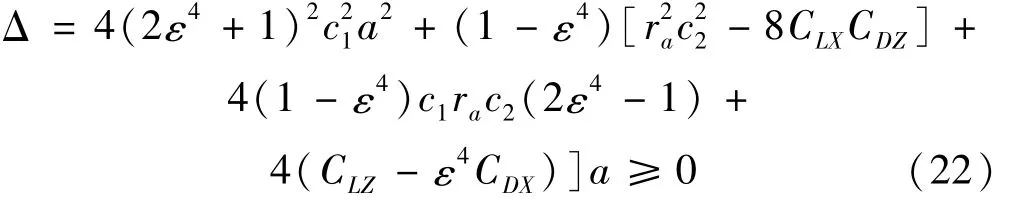
式中

在上游子导线尾流区的大部分位置均能满足此条件。且质量参数a必须满足：

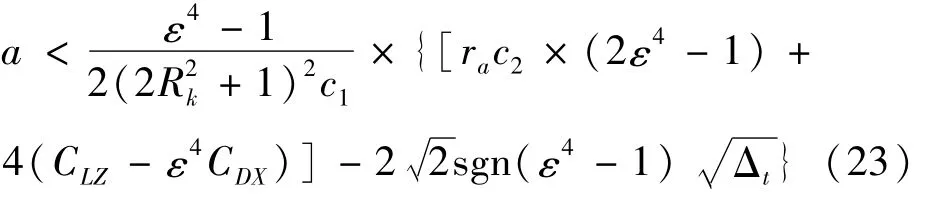
式中：

由上述条件可知，导线的质量参数影响其稳定性。通过求解方程（20）的根可得到导线系统失去稳定状态的临界缩减速度为：

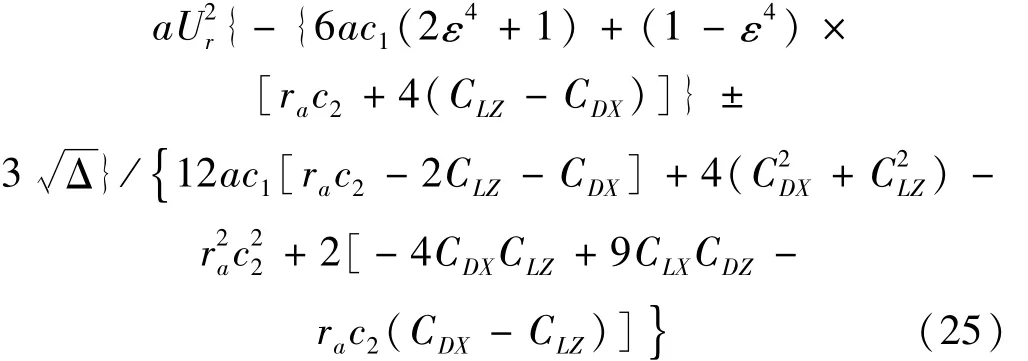
2．2 Hopf静态分岔

由方程（17）可知，当h0＝0时，其中一个特征根为零。此即为静态分岔的临界条件。这可利用振动原理来理解，通过振动方程（14）可看出，导线系统的气动刚度与－／2成正比，当均匀来流风速V0增大到一定的程度时，气动刚度将大于弹性刚度，使整个系统出现负刚度而导致其偏离平衡位置失去稳定状态。由h0＝0可求得静态分岔的临界缩减风速为：

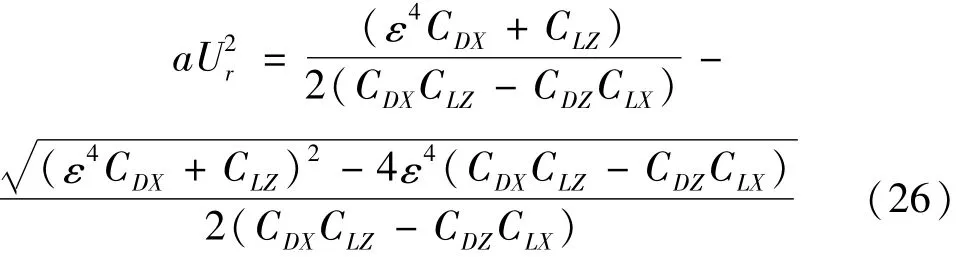
3 数值算例

振动系统发生不稳定与其无量纲质量参数a有关，由于空气的密度很小，典型架空输电线路工程中的分裂导线的无量纲质量参数a约为2×10－4。取导线直径d为30 mm，平均升阻力系数曲线取文献［6］结果，利用上述系统稳定性理论对处于上游子导线尾流区域中不同位置的下游子导线进行稳定性分析。计算工况选取无量纲坐标 X＝7、10、20、25，Z＝－4、－2、0、2、4，经MATLAB程序计算得到驰振临界风速Vcr随频率比fz／fx变化的规律，计算得出不同工况下的变化规律相似。当尾流中下游子导线相对上游子导线的坐标为X＝10、Z＝2时，下游子导线发生驰振的临界风速Vcr的Hopf分岔边界与静态分岔边界如图3所示。

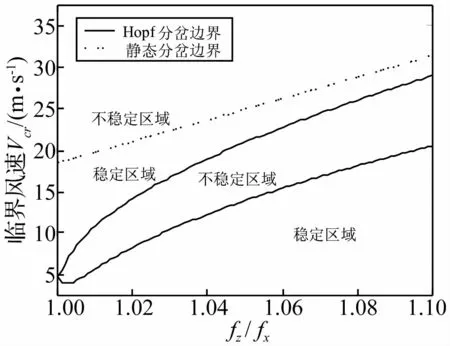
图3 两种分岔理论对应的临界风速Vcr随频率比 fz／fx的变化Fig．3 The critical wind speed Vcr with the frequency ratio fz／fx changes under the two bifurcation theory

由图3可看出，对于分裂导线这种无量纲质量参数a非常小的情形，只有当来流风速V0增大到气动刚度大于弹性刚度时，才会发生静态分岔，而在此之前尾流中的下游子导线已通过Hopf动态分岔方式失稳，发生尾流驰振，后者即为分裂导线中处于尾流中的下游子导线失稳机理。同时还可看出，频率比fz／fx的增大会提高导线系统发生尾流驰振的临界风速Vcr，工程中一般采用合理间隔棒的型号与布置位置来调谐不同方向的频率比，以提高系统的稳定性。

阻尼参数是导线振动系统的重要参数，通过计算研究阻尼参数的敏感性。计算工况选取为两子导线的相对坐标为X＝12、Z＝1．5，对振子模型中两方向的阻尼比 ζx、ζz均分别取 0、0．5%、1%、3%时，进行稳定性分析，可得到不同阻尼比下其驰振临界风速Vcr随频率比变化的规律如图3所示

图4 不同阻尼比对应的临界风速Vcr随频率比 fz／fx的变化Fig．4 The critical wind speed Vcr with the frequency ratio fz／fx changes under the damping ratio

由图4可看出，当阻尼比ζ从0增加到0．5%时，最小临界风速Vmincr仅增大2%。这说明阻尼比较小时对驰振临界风速边界区域的影响较小。当阻尼比ζ增大到一定的程度时，其会改变发生驰振边界区域，提高导线系统发生尾流驰振的最小临界风速Vmincr与临界频率比Rfcr＝fz／fx（小于该临界频率比将不发生尾流驰振），从而会减少其驰振区域，提高导线系统的稳定性。导线系统的阻尼主要是依靠其自身的阻尼效应，通过安装阻尼间隔棒只能局部改变系统的阻尼，对整个系统的阻尼提高比较小。从阻尼贡献抑制次档距振荡的角度看，安装阻尼间隔棒并不是控制与防治导线尾流驰振的有效措施。较为有效的措施是缩短次档距长度，优化阻尼间隔棒的安装间距，以产生较大的能量耗散，从而把次档距振荡抑制在安全限度内。

4 结 论

本文应用准定常理论，建立了分裂导线次档距振荡的振子模型，运用稳定性理论，推导了振荡发生临界风速的计算公式，并研究了不同参数情况下临界风速的变化曲线，主要结论如下：

（1）对于分裂导线的次档距振荡，尾流中的下游子导线首先是通过Hopf动态分岔方式失稳，从而发生尾流驰振。

（2）频率比的增大会提高导线系统发生尾流驰振的临界风速，工程中一般采用阻尼间隔棒，不等次档距安装，将间隔棒布置在接近振动的波峰而远离波节点的地方，充分发挥其振动阻尼作用，来调谐不同方向的频率比，以提高系统的稳定性。

（3）阻尼比较小时对驰振临界风速边界区域的影响较小，当阻尼比增大到一定的程度时，其会提高导线系统的稳定性。

［1］Simpson A．On the flutter of a smooth cylinder in a wake［J］．Aeronautical Quarterly，1971 feb：25－41．

［2］Simpson A．Wake induced flutter of circular cylinders：mechanical aspects［J］．Aeronautical Quarterly，1971 may．

［3］Cooper K R．Wind tunnel and theoretical investigations into the aerodynamic stability of smooth and stranded twin-bundled power conductors［R］．National Research Council of Canada Technical Report LTR－LA－115，1973．

［4］Cooper K R． A wind tunnel investigation for Alcan International into the effects of stranding on the aerodynamic stability of twin-bundle power conductors［R］．National Research Council of Canada Technical Report LTR－LA－115，1973．

［5］Tsui Y T．On wake-induced flutter of a circular cylinder in the wake of another［J］．Journal of Applied Mechanics，1977，44：194－200．

［6］Tsui Y T，Tsui CC．Two dimensional stability analysis of two coupled conductors with one in the wake of the other［J］．Journal of Sound and Vibration，1980，69（3）：361－394．

［7］Price S J．Wake induced flutter of power transmission conductors［J］．Journal of Sound and Vibration，1975，38（1）：125－147．

［8］叶志雄．输电线微风振动及次档距振荡控制研究［D］．武汉：华中科技大学，2009．

［9］冯学斌．输电线路多分裂导线次档距振荡的研究［D］．保定：华北电力大学，2006．

［10］Simpson A．On the Flutter of a Smooth Circular Cylinder in a Wake［J］．Aeronaut Q，1971，22：25－41．

［11］Doocy E S，A R H，Rawlins C B，et al．Transmission line reference book：wind induced conductor motion［M］．Electric Power Research Institute，Palo Alto，California，1979．

［12］Simiu E S R H． The wind effects on structures-wind engineering［M］．Shanghai：TongJi University Press，1992．