容积效应对某导弹发射装置液压系统的影响*
杜芳莉,陈志坚,董明德,杜 海
(1西安航空学院动力工程系,西安710077;2解放军边防学院,西安710108;3西安飞行自动控制研究所,西安 710065)
0 引言
反坦克导弹武器系统通常由弹药系统、发射系统及观瞄控制系统3个主要部分组成。相同技术状态的导弹在不同的发射条件下发射,其飞行性能存在差异。而发射装置要用到液压系统来执行导弹飞行的高低和方向的引导,伺服阀则是液压系统的一个重要组成部件[1]。如果出现故障则会导致导弹不按指定方位飞行,从而导致导弹不能正常发射,所以其性能的优劣对液压系统的影响很大。因此,它是液压控制系统的核心和关键[2]。文中结合实际工作经验,以某导弹发射液压系统伺服阀故障测试为例,对伺服阀产生的故障现象进行原因分析,并通过建立伺服阀AMESim结构参数化模型,在仿真计算基础上提出相应解决办法,并最终通过实际试验验证,说明容积效应对导弹发射装置中的液压系统具有一定的影响。
1 伺服阀测试台工作原理
伺服阀性能指标主要包括零偏、内漏、线性度、滞环以及死区等[3],文中重点说明伺服阀内漏指标在液压测试台中的测试。
图1给出了伺服阀静态流量特性测试原理[4-6],两个流量计分别用于控制腔流量和内漏流量的测试,其中L1用于内漏测试,L2用于控制流量测试,电磁阀用于两种测试状态切换(电磁阀应为通断两种状态)。由于负载腔流量计的量程受限,在测量大流量伺服阀时,需要通过电磁阀F1的上位直接与伺服阀B腔相连;只有在小流量伺服阀测试时,电磁阀F1在下位工作,负载腔流量通过流量计L2。文中所讨论的伺服阀内漏测试依靠流量计L1进行。
图中符号说明:伺服阀F2、电磁阀F1、流量计L2分别采用独立的安装块,各安装块之间采用硬管与硬接头连接。

图1 伺服阀静态流量特性测试原理
T1、T2、T3、T4、T5为试验台液压管路,其中 T1为 A负载腔与F1之间管路,长度约0.5 m,内径10 mm。T2为B负载腔与流量一端管路,长度约1 m,内径10 mm。T3为B负载腔与F1的管路,长度约0.3 m,内径10 mm。T4为流量计L2安装座与流量计之间管路长度约0.3 m,内径10 mm。T5为伺服阀回油口与内漏测试流量计L1之间管路,未涉及改动,可以忽略不计。
2 故障现象
某导弹发射装置液压系统用某型喷嘴挡板伺服阀的额定工作压力为21 MPa,内漏指标为:常值内漏不大于0.42 L/min,最大内漏不大于 0.55 L/min,经伺服阀测试台测试的最大内漏为0.62 L/min,不满足指标要求,详见图2。
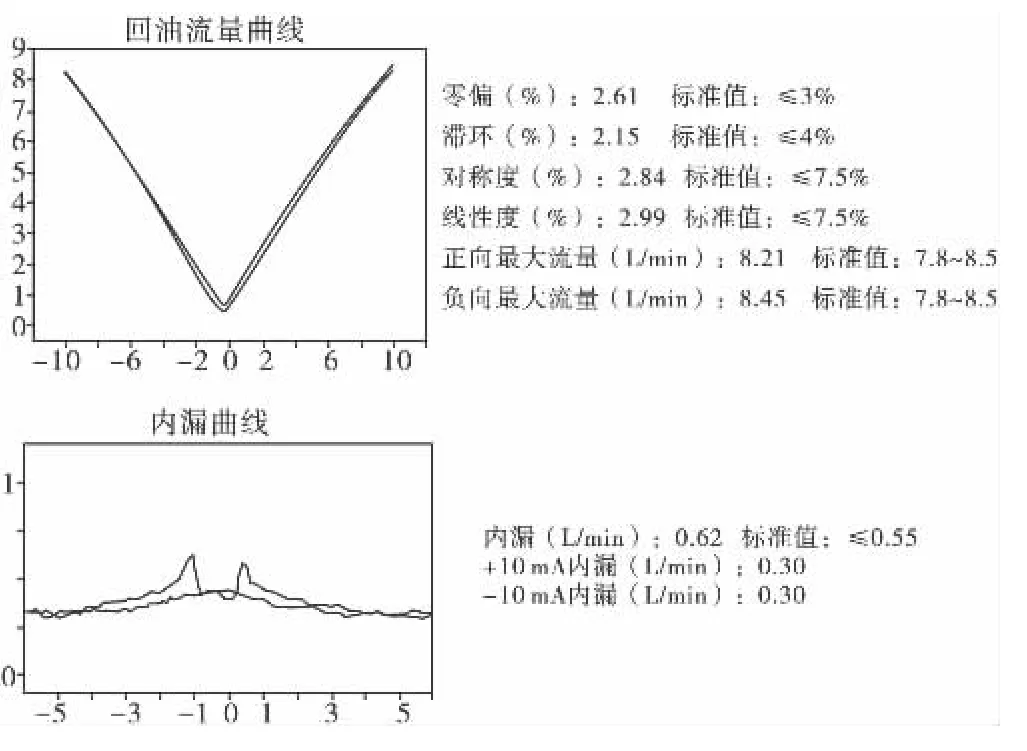
图2 实际伺服阀内漏测试曲线
3 故障原因分析
3.1 故障产生的原因分析
经过长期的研究及工作实践经验得知,影响伺服阀内漏的因素包括:伺服阀额定流量、伺服阀阀芯与阀套的配合间隙、伺服阀阀套阀芯的节流边遮盖状态、伺服阀喷嘴前的节流孔的尺寸以及前置级压力的大小是否满足设计要求、测试设备是否满足伺服阀内漏测试的要求等多个方面[7]。该型伺服阀为成熟产品,并已经过多年的批产加工,工艺成熟稳定。而本项目则是通过对检查内漏测试不合格伺服阀产品进行实测,得出以下结论:
1)阀芯与阀套的间隙满足设计图纸要求;
2)由于是新加工的零件,阀芯节流边保持尖边,原始加工重叠状态为保持0.003 mm左右重叠量的“零重叠”状态;
3)伺服阀喷嘴前的节流孔的尺寸以及前置级压力的大小满足设计要求;
4)常值内漏满足指标要求,排除了液压测试台上电磁阀(选用零泄漏电磁阀)的泄漏导致内漏测试超差的可能性;
5)本次测试内漏超标的伺服阀测试台为新研产品,为了满足批量产品调试的需求,提高测试设备的工作效率,对老试验台进行了自动化程度改造,测试设备使用电磁阀替代了原试验台的手动机械开关。经检查,由于管路排布问题使得控制腔连接油路长度比原试验台有所增加。
通过分析,认为测试台管路长度的增加是导致伺服阀内漏增加的原因。因为增加管路长度,使得贮存在管路中油液的体积增加。在内漏测试过程中,当伺服阀阀芯经过中位时,伺服阀控制腔中的压力发生了变化,由于容积效应的影响,压力的变化导致伺服阀控制腔的油液体积发生了变化,多余的油液流入伺服阀内漏中,从而导致伺服阀的内漏超差。
3.2 量化理论分析
1)压力变化引起的油液体积变化
在实际测试中根据油液弹性模量计算公式βe=ΔP/(ΔV/V1)得出压力油腔中压力变化引起的油液体积变化量为:

其中:ΔV为压力油腔中油液体积的变化量;βe为油液的弹性模量[8-9],βe=6.9 × 102MPa;ΔP为油液压力的变化量,ΔP=21 MPa;V1为控制腔以及连接管路的体积,文中只考虑T2和T3油管的体积。

代入ΔV=ΔP/(βe/V1)式中,经计算ΔV=3 107mm3。
2)压力变化所需的时间
根据实际的测试得出伺服阀的压力增益曲线如图3所示,其中压力增益为Kp=98.17 MPa/mA,通过压力增益换算ΔP所需的电流为,将上述ΔP=21 MPa代入,经计算ΔI=0.214 mA。根据测试条件,幅值为10 mA,频率为0.005 Hz,换算所需的时间,则压力变化所需的时间为:

图3 伺服阀实际压力增益测试曲线

3.3 仿真分析
文中采用AMESim仿真软件[10-15],依据实际伺服阀的结构参数,建立AMESim结构参数化模型如图4。
此伺服阀结构参数设定为额定进油压力Ps:210 kg/cm2,额定回油压力Rs:≯10 kg/cm2,额定控制电流I:±10 mA,额定空载流量 QH:7.5 L/min,零位漏损Q0:< 0.55 L/min,阀芯尺寸:4.5mm,阀芯轴肩尺寸:2.8 mm,阀芯、阀套间隙尺寸:0.003 mm。
某型伺服阀仿真参数据工作实际工作环境设定为电流:±10mA,频率:0.02 Hz,控制腔油管参数:管长为T2+T3=1 300 mm,管径为10 mm。通过对管路优化前的内漏测试进行仿真得出如图5~图7的曲线图。
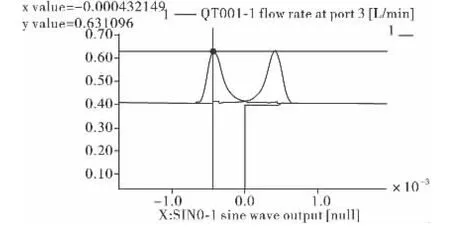
图6 管路优化前的内漏仿真曲线细节图

图7 管路优化前的内漏实际测试曲线
由图5~图7可见,伺服阀内漏仿真值为0.65 L/min,实测值为0.62 L/min,仿真曲线与实测曲线比较吻合。
依据之前的故障原因分析,通过减小伺服阀控制腔管路的体积,可以减小管路容积效应对伺服阀内漏测试的影响。将原模型中T2和T3油管的长度减小为500 mm,管径减小为6 mm,进行仿真计算。管路优化后据工作实际需要设定仿真参数为电流:±10 mA,频率:0.02 Hz,控制腔油管参数:管长为 T2+T3=500 mm,管径为6mm。通过对管路优化后的内漏测试进行仿真得出曲线如图8~图10所示。
由图8~图10可见,伺服阀内漏仿真值为0.46 L/min,实测值为0.49 L/min,仿真曲线与实测曲线比较吻合。
通过仿真与实际测试结果对比,优化伺服阀控制腔连接管路长度,减少了液压管路容积对于伺服阀内漏的影响,满足了伺服阀内漏指标的测试需求。

图8 管路优化后的内漏仿真曲线

图9 管路优化后的内漏仿真曲线细节图

图10 管路优化后的内漏实际测试曲线
4 结论
通过针对某导弹发射装置液压系统伺服阀的内漏超差问题的分析与研究,得出工作油液的可压缩性以及容积对于导弹发射装置液压系统性能有一定的影响,在工程实际应用中,对于从事导弹发射装置液压系统的技术人员有一定的借鉴作用。
[1]陈彬,易孟林.电液伺服阀的研究现状和发展趋势[J].液压与气动,2005(6):5-8.
[2]易建钢,湛从昌,吴琼进.电液伺服阀动态特性测试中复合数字滤波算法研究[J].液压与气动,2004(2):15-16.
[3]李健锋,袁锐波,张自华.电液伺服测试系统研究[J].液压与气动,2007(12):65-67.
[4]曹鑫铭.液压伺服系统[M].北京:冶金工业出版社,1991.
[5]傅连东,陈奎生,曾良才,等.电液伺服阀的改进型智能故障诊断研究[J].武汉科技大学学报:自然科学版,2007,30(2):164 -167.
[6]宋晓军,刘帮成.电液伺服阀测试台液压系统设计[J].机床与液压,2011,39(12):32 -35.
[7]刘自磊,吴百海,邹大鹏.电液伺服阀自动测试方法的研究[J].机床与液压,2005(11):114-116.
[8]岳国良,李楠.航空液压油体积弹性模量的测定方法[J].合成润滑材料,2011,38(1):19 -21.
[9]王静,龚国芳,杨华勇.油液弹性模量检测装置设计及仿真分析[J].液压与气动,2006(7):34-36.
[10]付永领,祁晓野.AMESim系统建模和仿真[M].北京:北京航空航天大学出版社,2006.
[11]朱学彪,陈奎生.对于三级电液伺服阀的新型仿真与研究[J].机床与液压,2005(2):97-98.
[12]罗福胜,傅连东,付曙光,等.一种新型电液伺服阀的建模与仿真[J].矿山机械,2011,39(5):95-99.
[13]Affred Lynn,Edzko Staid,Moji Eshraghi,etal.Modeling hydraulic regenerative hybrid vehicles using AMESim and Matlab/Simulink,SPIE Proceedings,2005 vol.5808.
[14]余佑官,龚国芳,胡国良.AMESim仿真技术及其在液压系统中的应用[J].液压气动与密封,2005(3):28-30.
[15]李阔,郭迎清.AMESim仿真技术在航空动力控制系统中的应用[J].计算机仿真,2009,26(1):107-110.
[16]邢科礼,冯玉,金侠杰,等.基于AMESim/Matlab的电液伺服控制系统的仿真研究[J].机床与液压,2004(10):57-58.

