基于支持向量回归机的导弹平台调平过程模型辨识*

卢文忠，刘丙杰，冀海燕

（海军潜艇学院，山东青岛 266042）

0 引言

平台调平是某导弹测试、发射过程中的重要程序，主要完成对平台框架坐标系的OPXP轴与OPZP轴进行调平，从而使框架坐标系XPOPZP平面与当地的水平面平行。平台调平回路有X、Z两条，均由石英挠性摆式加速度计、调平放大器（含校正网络、功率放大器）及平台稳定回路组成。

由于平台调平装备结构、调平过程涉及因素众多，难以建立精确的平台调平解析模型，从而影响了仿真的逼真度以及训练的真实性。

支持向量回归机作为一种性能良好的模型辨识方法，在众多领域得到了广泛应用［1－3］。本系统根据历史调平数据，利用支持向量回归机对平台调平回路进行模型辨识，从而产生逼真的调平数据，为某导弹的全过程训练提供数据支持。

1 支持向量回归机原理

支持向量回归机是从数据分类问题的研究中发展而来的，将估计指示函数（对模式识别问题）中得到的结论推广到估计实函数（回归）中，且引入一种新的损失函数——ε不敏感损失函数，这样就可以得到基于支持向量机的回归估计方法。

给定训练样本（xi，yi），i=1，2，…，l，若是在线性情况下，定义如下线性函数集合:

可以从上式估计函数，损失函数一般情况下定义为ε不敏感损失函数［3］:

ε不敏感损失函数的优点是可以使估计具有鲁棒性，而且得到的解是稀疏的，而这一点对在高维空间用大量数据估计依赖性关系来说是非常重要的。在这里采用线性ε不敏感损失函数:

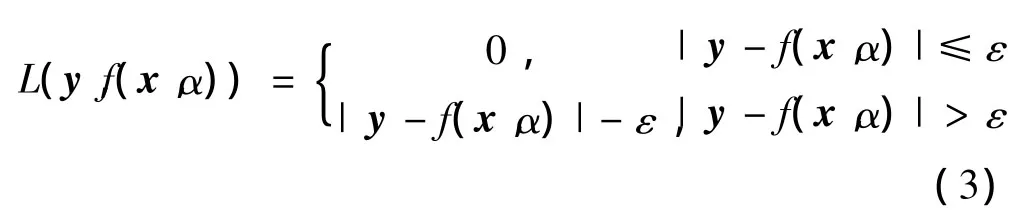
基于结构风险最小化原理，可以将问题转化为:

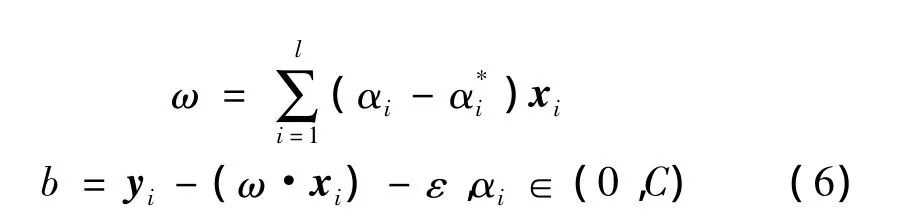
由 ω、b 与 αi、α*i的关系，可以得到最优估计函数:由上式可知，ω的最优估计值仅与αi≠α*i，i=1，2，…，l所对应的样本向量xi有关，这样的样本向量xi就称为支持向量，支持向量只占总样本的一小部分，所以利用支持向量可以使训练过程大大简化，而且使得到的估计函数具有很好的推广能力。

2 平台调平过程时间序列模型辨识

从某导弹平台调平过程可以看出，调平的主要目的是对7个参数进行调整，包括俯仰角θ1、偏航角θ2、滚动角 θ3、加速度计当量 wx、wy、wz、调平输出当量 Ct等［5］。所以，要建立平台调平过程模型，就是对上述7个参数进行辨识。文中对上述各参数各建立一个支持向量回归机模型组成平台调平过程时间序列模型，原理如图1所示。

图1 平台调平模型辨识原理

假设参数X的时间序列样本为:

支持向量回归机的输入、输出样本分别为:

则支持向量回归机模型为:

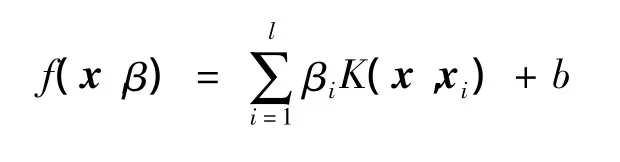
3 仿真实例

某导弹平台调平参数部分样本值如表1所示。

表1 某导弹平台临射调平数据

本系统利用上述数据，采用支持向量回归机建立某导弹的平台调平过程模型。支持向量机参数C=10 000，σ2=0.01，核函数选择 RBF 核函数，仿真平台为Matlab 6.5，平均预测误差:2.56%，计算结果见表2。

表2 平台调平过程模型辨识仿真预测误差

其中俯仰角、滚动角预测结果如图2所示。

图2 某导弹平台调平仿真结果

4 结论

从仿真结果可以看出，支持向量回归机对某导弹的平台调平过程模型辨识精度比较高，其中俯仰角辨识精度最高，达到0.07%，调平输出当量模型辨识精度较低，达到13.3%，总体预测精度达到2.56%，完全满足了平台模拟仿真的需求。

［1］杜树新，吴铁军.用于回归估计的支持向量机方法［J］.系统仿真学报，2003，15（11）:167－169.

［2］张心光，邹早建.基于支持向量回归机的传播操纵响应模型辨识［J］.上海交通大学学报，2011，16（4）:228－231.

［3］尉询楷，李应红.基于支持向量机的航空发动机辨识模型［J］.航空动力学报，2004，19（5）:684－688.

［4］沈丽民，李军显.基于支持向量机的雷达高分辨距离像识别［J］.弹箭与制导学报，2009，29（2）:231－234.

［5］杨海波，洪贞启，马暄.潜射导弹捷联惯性平台快速调平补偿方案研究［J］.战术导弹技术，2010（4）:48－50.