悬浮子弹降落与悬浮过程弹道特性动力学分析*

雷 伟，钱建平，季溢栋，居仙春

（南京理工大学机械工程学院，南京 210094）

0 引言

悬浮弹系统是一种新型的“被动式”防御武器，它是一种屏障式武器，可以构筑有效的防御系统。我国对悬浮装置的结构、气囊空中充气技术以及悬浮弹空中姿态有相关研究［1－2］。文献［3］提出了一种驱动旋翼的方法使悬浮弹达到悬浮。

文中采用旋翼结构，通过对悬浮子弹的工作过程研究，包括母弹开舱抛撒、无翼惯性下降、旋翼张开无动力驱动惯性下降、有动力驱动旋翼减速至稳定悬浮等阶段，并结合算例进行数值分析得到最佳的驱动方式和驱动力矩。

1 概述

1.1 弹道特性

根据悬浮子弹的工作过程将悬浮子弹的弹道分为4个阶段，如图1所示。悬浮子弹经母弹开舱自由下落段（Ⅰ），减速减旋段（Ⅱ）可分为两种方式:开翼立即驱动至稳定悬浮（Ⅱ-a）;先开翼无动力驱动惯性下降（Ⅱ-b1）再有动力驱动至稳定（Ⅱ-b2），稳定悬浮段（Ⅲ），有翼惯性下降无动力驱动段（Ⅳ）。并将开始有动力驱使至稳定悬浮的时间称为过渡时间，即Ⅱ-a和Ⅱ-b2段所用时间。悬浮子弹经过渡段到达稳定悬浮（Ⅲ）构筑防御屏障，这也正是其与普通子母弹的最大区别。

图1 弹道特性示意图

1.2 结构特性

悬浮子弹由旋翼、驱动装置和弹体三部分组成，如图2所示。旋翼与驱动装置之间以及驱动装置与弹体之间的连接分别称作轴承1和轴承2。为了使弹体更好的减旋，下文中会在某一弹道阶段采取旋翼与驱动装置、驱动装置与弹体固结在一起的形式（即不产生相对转动），分别称作轴承1、2固联，不固结在一起称作轴承自由（不固联）。由于驱动装置与弹体之间的转速不同，将驱动装置与弹体分别看作刚体1和刚体2采用两刚体建模能够更好的模拟真实情况。

图2 悬浮弹结构及坐标示意图

2 旋翼下降过程动力学模型

2.1 旋翼展开后无动力驱动时力学模型

由于悬浮子弹从母弹抛出后有很高的迎面速度，产生相对翼片自下而上的相对气流，其速度大于旋翼的诱导速度。相对气流U自下而上斜向指向桨叶，叶素来流角为负值。因叶素所产生的升力Y与相对气流合速度U垂直，所以叶素的升力Y向前倾斜，在旋转面上的分力Qy指向前方，起拉着旋翼继续旋转的动力作用;而空气阻力X形成的旋转阻力Qx起阻止旋翼旋转的作用。当旋翼各片桨叶的Qy和Qx取得平衡时，旋翼就能在自下而上的相对气流作用下保持稳定自转，如图3所示。

叶素上的相对气流速度U可表示为:

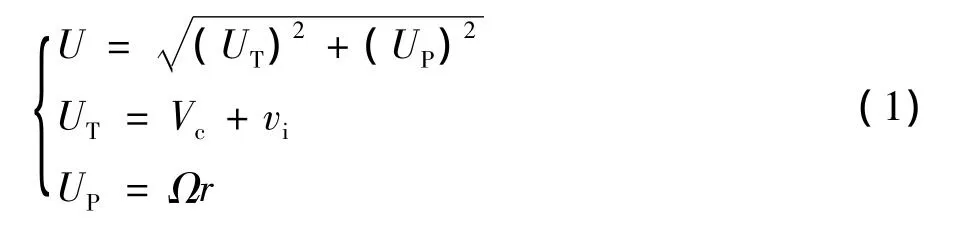
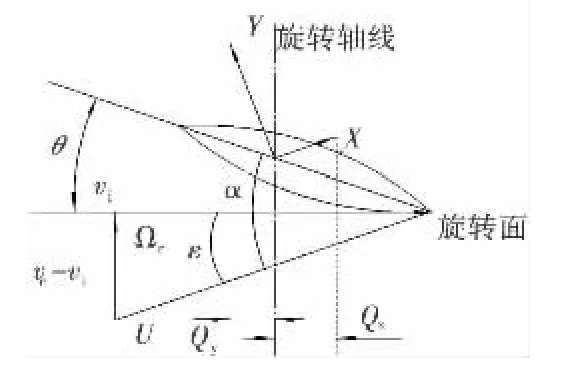
图3 叶素在下降状态下的受力分析

式中:UT、UP分别为桨叶剖面的切向速度和轴向速度;Ω、r为桨叶旋转速度和桨叶剖面径向位置;Vc、vi分别为旋翼浆盘迎流速度和与之对应的诱导速度，此时在高下降率的情况下，经典的动量理论不再成立［4］。

这样，叶素上的升力Y和阻力X有:

式中:Cl、Cd为升力系数与阻力系数［5］。来流角ε和攻角α可分别表示为（向上为正），α=θ－ε，θ为叶片安装角，c为桨叶当地弦长。则微元为拉力:

微元阻力矩:

因此，得出了悬浮子弹从母弹抛撒出后无动力驱动时展开旋翼，旋翼转速的变化规律:

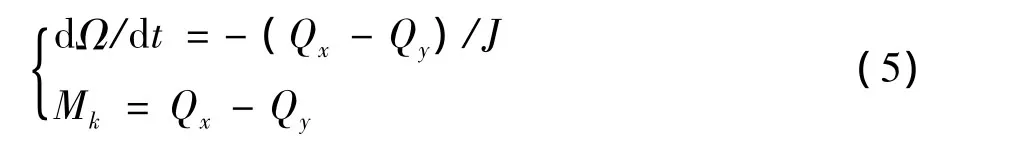
式中:J为旋翼的转动惯量;Mk为旋翼对驱动装置的反作用力矩。直至Qy和Qx相等时，旋翼稳定自转。将式（4）代入式（1）～式（3）便能得到无动力驱动时的升力T（t）。

2.2 旋翼有动力驱动时力学模型

旋翼开始有动力驱动时，输入转矩会给定一扭矩M。接下来分两种情况:

1）Vc＞vi时，Qy和Qx的方向仍然相反，输入力矩为了使旋翼加速，此时与Qy方向一致。旋翼的转速随时间变化:

随着转速与提升力的增加，悬浮子弹下降速度势必会逐渐减小，直至出现Vc≤vi时，ε由负值变为正值，力矩方向随之发生变化。

2）Vc≤vi时，Qy和Qx的方向相同，有:

至此，已经得到了完整的旋翼下降过程力学模型，接下来建立悬浮子弹刚体弹道模型。

3 悬浮子弹两刚体外弹道模型

3.1 坐标系的建立与变换

首先建立地面惯性坐标系O-X0Y0Z0，原点O为悬浮弹子弹抛撒点的地面投影点，OX0轴水平沿射向，OZ0轴铅直向上，OY0轴由右手法则确定;驱动装置固连坐标系O1-X1Y1Z1，原点O1为驱动装置质心，O1Z1在铅直面内指向弹顶，O1Y1在铅直面内垂直于O1Z1轴，O1X1由右手法则确定;弹体固连坐标系O2-X2Y2Z2，原点O2为弹体质心，各轴与O1-X1Y1Z1系平行;弹体基准坐标系O2-X0Y0Z0，原点O2为弹体质心，各轴与O-X0Y0Z0系平行。各坐标系如图2所示。

坐标变换只需考虑两组变换即可。O2-X0Y0Z0与O2-X2Y2Z2之间可由3个欧拉角:进动角ψ2，自转角φ2，章动角θ2转换而来，转换矩阵用[ ]A 表示如下。O2-X2Y2Z2与 O1-X1Y1Z1之间只是坐标原点移动O2O1，故转换矩阵同样可用[]A 表示。另外有:[]A－1=[ ]AT。

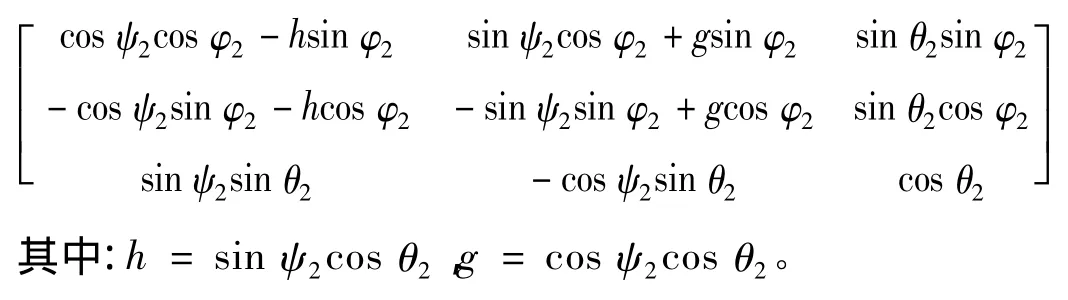
3.2 运动方程的建立

通过对各刚体所受力、力矩的分析，将所有的力投影到 O-X0Y0Z0坐标系上，所有的力矩投影到O2-X2Y2Z2坐标系上得:

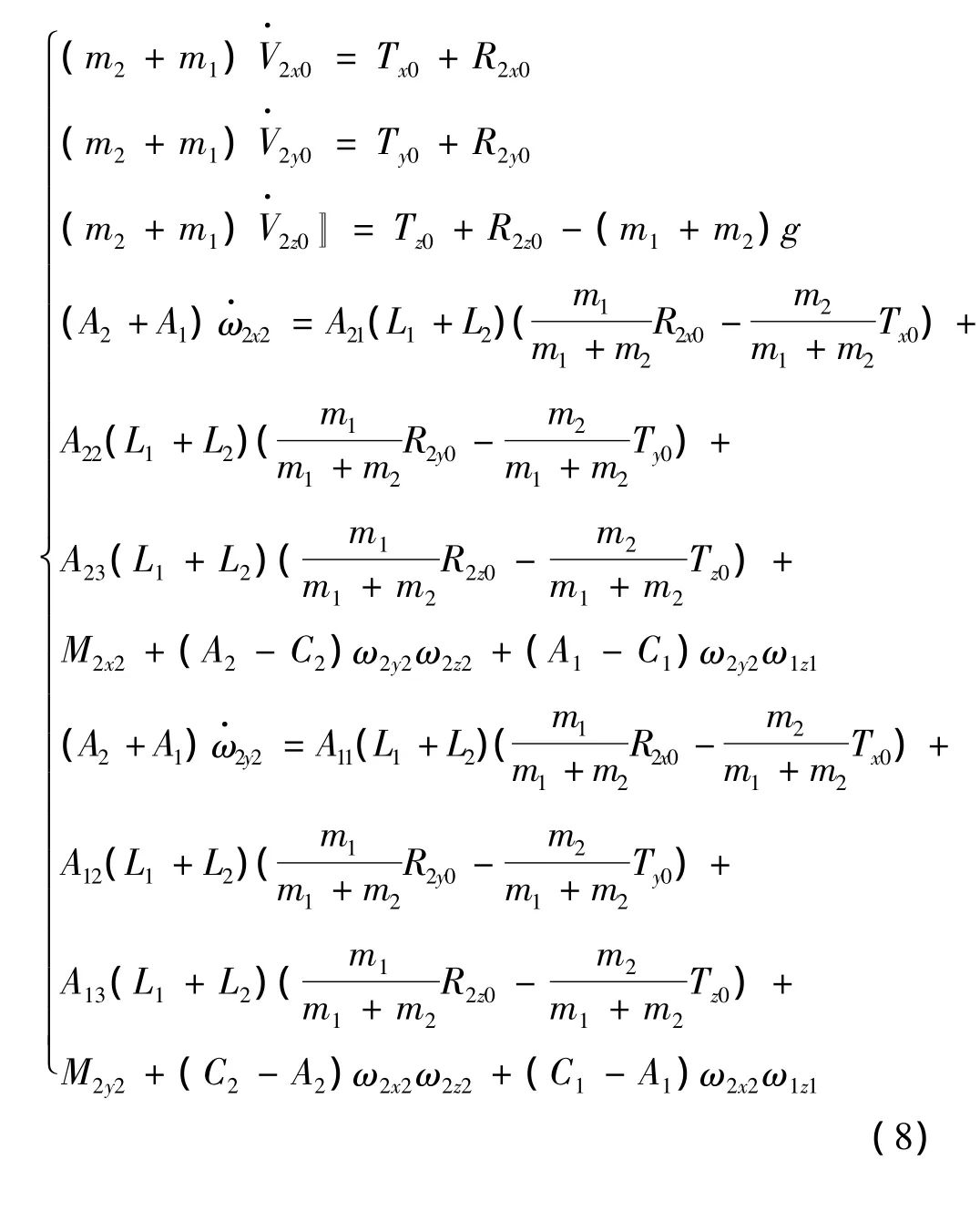
轴承1、2之间的关系得到方程:

式（8）、式（9）中:下标带有 xi、yi、zi表示通过坐标变换投影到O-XiYiZi（i=0，1，2）坐标系中;m1和m2、A1和A2、C1和C2分别为驱动装置刚体与弹体刚体的质量、赤道转动惯量、极转动惯量;L1和L2分别为O1D和O2D的距离;T为旋翼的拉力;R2为弹体所受的空气动力，包括阻力Rx2、升力Ry2和马格努斯力;M2为弹体所受的空气动力矩，包括弹体的极阻尼力矩Mxz2，静力矩Mz2，赤道阻尼力矩Mzz2

［6］;Mf1和Mf2分别为轴承 1、2的摩擦力矩，有:Mf=f0（vn）2/3d3m，dm为轴承平均直径，f0为考虑轴承结构和润滑方法的系数，n为轴承连接体之间相对转速，v为润滑剂的运动粘度;Mk为旋翼的反扭矩，由旋翼的力学模型中可得到。

3.3 四元数法替代欧拉角

欧拉角之间的关系:

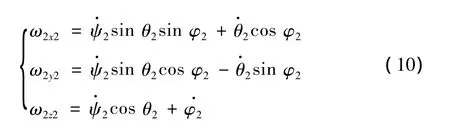
由于欧拉角的表示方法在计算中容易出现奇点而停止运算，文中采用四元数法替代欧拉角［7］:

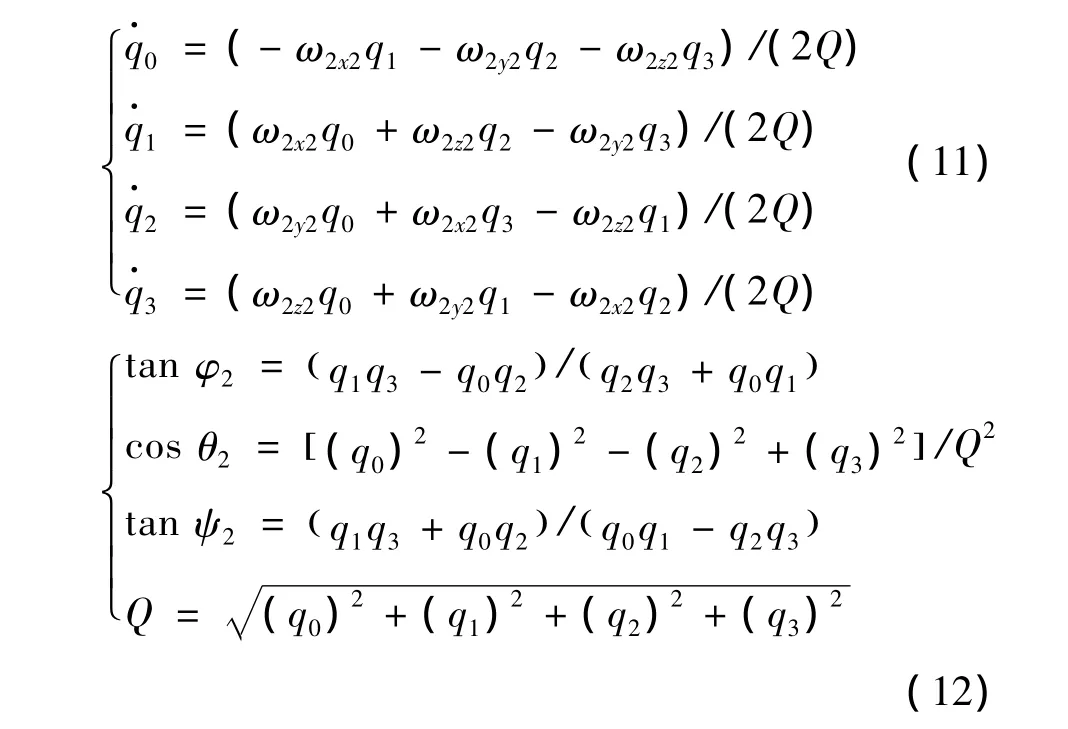
至此，已经得到了完整的旋翼下降过程力学模型和悬浮子弹刚体弹道模型，将旋翼力学模型中的T（t）、Mk代入弹道模型中便能得到悬浮弹的弹道轨迹。

4 初始参数

子弹出舱参数:母弹存速300 m/s，抛撒速度40 m/s，弹道倾角60°，子弹出舱转速10 000 r/min，开舱高度1 000 m。

空气密度 ρ=ρon（1 －2.19 ×10－5h）4.4016，其中 ρon=1.293 kg/m3为地面空气密度，h为高度的变化。其他参数如表1所示。

表1 弹型与翼型相关参数

采用VB编写仿真程序，以时间为自变量利用四阶龙哥库塔法对Ⅰ、Ⅱ、Ⅲ段弹道方程进行数值计算分析。

5 只开翼，不驱动分析

在给定的初值条件下，子弹从母弹抛出后，让其自由下落，7.6 s便已落地，落地时的z方向速度（下称落速）仍然有94.5 m/s，弹体转速仍然有84.5 r/s。

图4、图5是3种固联方式下高度和弹体转速随时间变化曲线。可以看出，固联方式的不同对弹体减速效果以及落地时间差别并不大，但对弹体减旋的效果影响却很大。

图4 时间－高度 图5 时间－弹体转速

考虑到弹体一直处于高速旋转状态对结构的要求会更高，三种固联方式对减速效果几乎相同的情况下（落地时间分别为 19.03 s、19.66 s、19.76 s）采用轴承1、2都固联相对于其他两种方式在弹体减旋上效果更好。因此，综合考虑此阶段采用轴承1、2都固联的方式是最佳的。

6 驱动旋翼分析

6.1 确定最佳驱动方式

由于此时旋翼已经驱动，轴承1必须自由。假定悬浮子弹在150 m必须进入稳定悬浮阶段（落速小于10 m/s）。按照驱动方式的不同将其分为直接驱动（Ⅱ-a）和先开翼减速减旋一段时间再驱动（Ⅱ-b1+Ⅱ-b2）两种方式。首先给定正好能够克服悬浮子弹自身重力的驱动力矩，取M=0.056 N·m。

图6是在轴承2不固联情况下两种驱动方式高度随时间变化的对比。可以看出，Ⅱ-b的曲线全部在Ⅱ-a曲线之上，这说明先开翼后驱动的方式能够滞空的时间更长一些;图7是弹体转速随时间的变化曲线，显然先开翼后驱动的方式对弹体的减旋效果比较好，而且对比2轴承的固联方式可以看出，2不固联的方式能够在驱动旋翼以后弹体仍然保持减旋状态，当2固联时由于驱动旋翼以后旋翼的转速大于弹体的转速，致使它们之间的摩擦力矩仍会给弹体一个加速旋转的作用。

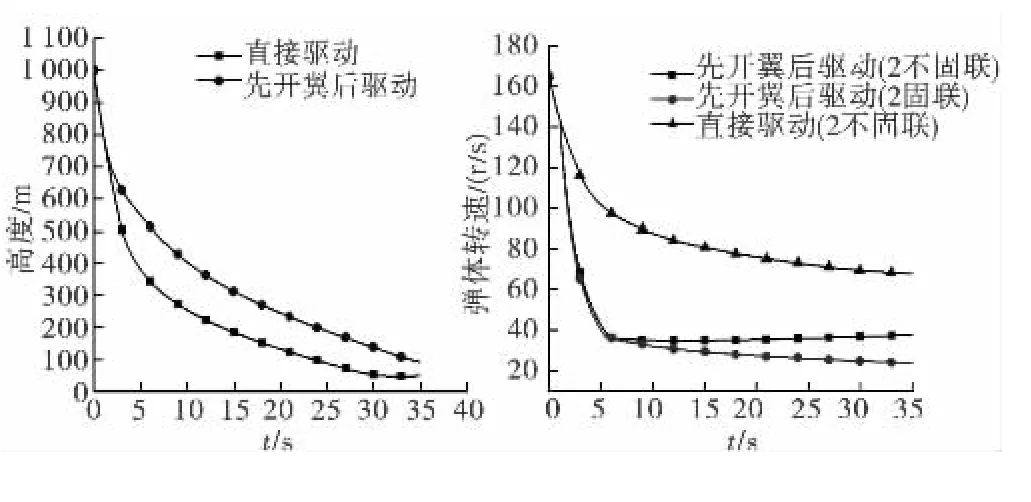
图6 时间－高度 图7 时间－弹体转速

综合以上对比，采用先开翼减速减旋一段时间，此时1、2都固联，然后再使1、2都不固联驱动旋翼是最佳的驱动方式。此方式能够更快的减速，弹体能够更好的减旋，而且有更长的滞空时间。但是无论哪种驱动方式过渡时间都很长。因此，需要通过增大驱动力矩的方法来减少过渡时间。

6.2 确定最佳驱动力矩

由于需要悬浮子弹在一定的驱动能量下，更长时间的处于悬浮段才能更有效的构筑防御屏障。因此，通过增加驱动力矩的方法减小过渡时间是必要的。采取上述确定的最佳驱动方式，对比1.2M、1.4M、1.6M、1.8M、2.0M、2.2M（M 是克服自身重力所需要的驱动力矩，M=0.056 N·m）时的弹道模型。

表2是800 m开翼高度不同驱动力矩（M的倍数）下所用过渡时间表，图8是过渡时间随驱动力矩增大的变化曲线。

表2 800 m开翼不同驱动力矩下过渡时间（s）

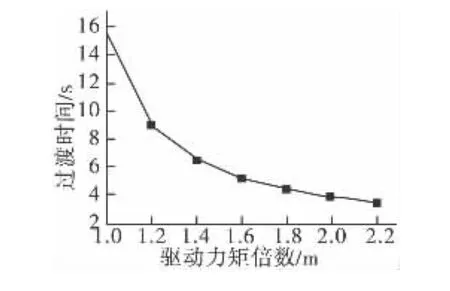
图8 驱动力矩倍数－过渡时间

可以看出，虽然随着驱动力矩的增加过渡时间在减小，但属于一个慢慢进入平缓的过程，在1.8倍之后基本进入水平阶段。然而在一定能量的情况下，驱动力矩越大能够驱动的时间也就越短。另外，悬浮弹在以大于M的驱动力矩减速到达悬浮段后必须有一个减小驱动力矩至M的过程，否则悬浮子弹会继续上升。越大的驱动力矩减小至M对结构的要求也会越困难。综合考虑过渡时间、一定能量下能够产生的驱动时间以及对结构的要求，选取1.4～1.8M之间驱动减速是最合适的。

7 结论

1）悬浮子弹在展开旋翼未驱动的情况下比自由下落子弹能够延长11.5 s左右落地，此时的最佳开翼方式是轴承1、2都固联的方式。

2）给出了悬浮子弹的最佳驱动方式是:先轴承1、2都固联减速一段时间再轴承1、2都不固联驱动旋翼。此驱动方式能够更快的减速，弹体能够更好的减旋而且有更长的滞空时间。

3）给出最佳的驱动力矩是刚好能够克服自身重力所需力矩的1.4～1.8倍之间，此时的过渡时间在4.5 ～6.5 s之间。

［1］闫红红，胡勇，张亚.空中悬浮装置的结构设计［J］.机械工程与自动化，2009（3）:155－156.

［2］钱立志，陶声祥，刘玉文.利用弹道方程计算悬浮弹射击诸元［J］.火力与指挥控制，2008，33（7）:19－21.

［3］胡西博，钱建平，季溢栋，等.涡轮驱动悬浮装置动力特性分析和试验［J］.四川兵工学报，2013，34（3）:21 －25.

［4］曹栋，曹义华.垂直下降状态下的旋翼三维流场数值模拟［J］.北京航空航天大学学报，2012，38（5）:641－647.

［5］李振波，陈佳品，张琛.低雷诺数四旋翼飞行器升力分析与计算方法研究［J］.中国机械工程，2005，16（7）:249－251.

［6］袁子怀，钱信芳.有控飞行力学与计算机仿真［M］.北京:国防工业出版社，2001.

［7］杨启仁.子母弹飞行动力学［M］.北京:国防工业出版社，1999.