基于R/S分析的黑河出山年径流量灰色预测

李建林，昝明军，李宝玲

(河南理工大学资源环境学院，河南焦作 454003)

0 引言

水资源短缺是制约干旱半干旱地区生产生活和社会经济发展的主要因素之一［1］，径流量的科学预测对该地区水资源合理分配和社会-经济-生态可持续发展具有重要作用。21世纪初，黑河流域开始实施干流水量统一调度，并取得了较好的效果。但目前黑河水量调度工作仍存在一系列的问题，譬如无工程控制、无径流预报、调度手段单一和水量调度实时性较差等［2］。莺落峡水文站是黑河出山径流量的控制站，此处流量的多少直接影响整个流域经济、社会发展和生态环境保护［3］。所以，黑河出山年径流预报研究对增强黑河干流水量调度工作的实时主动性、提高水量调度精度具有重要的现实意义［2］。

径流过程受大气降水、流域自然地理条件、人为因素等诸多因素影响，具有典型的非线性运动特征［4-5］。20世纪中叶以来，非线性科学成为自然科学进步和发展的主要标志，分形理论是非线性科学的重要理论之一［6］。在我国，将分形理论应用于径流过程的研究开始于1998年，其中一个重要应用方向是利用R/S(重标极差)法进行径流序列的分析［7-9］。但在求出Hurst指数验证径流序列具有分形特征之后，该如何进行更为深入的研究，一直没有突破。

径流变化也具有明显的灰色特征。在我国，将灰色理论应用于径流量的预测开始于20世纪80年代，至今该理论的应用已经相当成熟［10-11］。为了克服预报随机波动性较大的序列时拟合较差、精度降低的缺点，一些学者采用灰色理论与其他理论(BP神经网络、马尔科夫过程等)相结合的方法，对其进行了改进，效果较好［12-13］。基于此，本研究采用R/S分析与灰色理论相结合的方法对黑河出山径流量进行预测，以期R/S灰色预测模型的结果对黑河干流统一调水有一定的参考价值;同时探讨分形和灰色理论在径流过程研究中的进一步应用。

1 研究区概述

黑河发源于祁连山北麓，干流全长821 km，流域范围介于98°～101°30'E，38°～42°N 之间，流域总面积为14.29×104km2［14］。黑河流域处于青藏和蒙新高原交汇地带，垂直地带地貌景观鲜明。其南部是祁连山地，中部是走廊平原，北部是山地和阿拉善高原。地势西高东低，南高北低［15］，整个流域以高山、绿洲、戈壁和断续分布的沙漠为主要自然景观。以莺落峡和正义峡划分上、中、下游:莺落峡以上为上游，是径流的主产流区;正义峡以下为下游;莺落峡与正义峡之间为中游，是水资源的主要利用区［16］。

莺落峡水文站(38°48'N，100°11'E，海拔 1 710 m，1944年设站观测)集水面积10 009 km2，是黑河干流出山径流量的控制站。其总径流量15.523 9×108m3/a，多年平均流量49.225 9 m3/s，径流模数4.918 2 L/(s·km2)。径流补给来源以大气降水、冰雪融水和地下水为主，径流年内分配不均匀。上游东岔为八宝河，西岔干流为黑河，这两股干流在青海省祁连县黄藏寺汇合后进入甘肃省境内，在莺落峡出山口进入张掖灌区［17］(图1)。

2 资料来源与研究方法

2.1 数据来源

本研究针对黑河流域莺落峡水文站年径流实测数据(1949—2011年)进行分析与预测。

2.2 R/S分析法

2.2.1 基本原理。R/S分析法是一种描述分形结构的有效方法，其基本思想是改变样本序列的时间尺度，研究其在不同尺度范围内的统计规律，从而进行大小时间尺度间的相互转换［18］。该方法能从分形时间序列中区分出随机序列和非随机序列，为径流量时序的复杂性演变提供一种有效的非线性科学预测方法。通过Hurst指数可以判定径流量时间序列的分形结构和状态持续性;通过平均循环长度可以估算系统的记忆时间长度［19］。

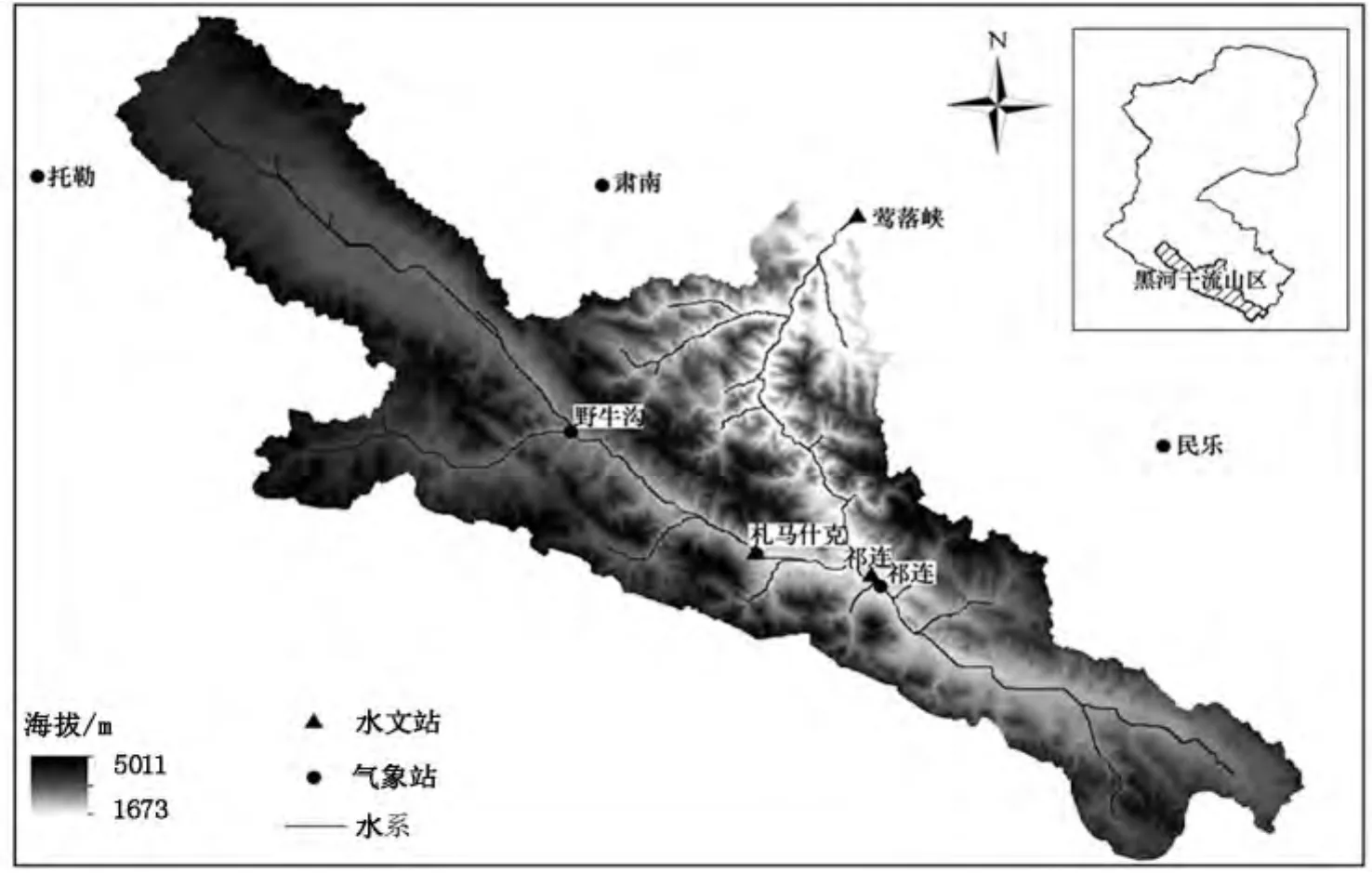
图1 黑河流域上游水系及主要水文和气象站点示意图［17］Fig.1 River system and important gauge stations and weather stations in the upper reaches of Heihe River

对于一个非随机过程序列，首先要求满足:

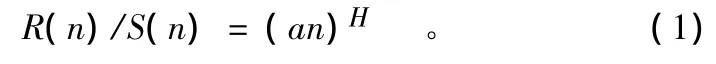
式中:R(n)/S(n)为重标极差;n为增量区间长度;a为常数;H为Hurst指数。作为分形现象的表征参数，Hurst指数H是R/S分析法中一个稳定而有效的统计量(0≤H≤1)。若 H=0.5，径流量序列为随机序列;0≤H＜0.5，径流量序列则为一种反持久性序列，即若序列开始有上升趋势，那么它将会出现下降趋势;0.5＜H≤1，径流量序列则具有状态持续性，即存在长期记忆性，表现为分形时间序列——未来与过去呈现相同的变化趋势;且其记忆性不随时间标度而变化，即不同增量(日、月、年等)序列间具有相同的统计规律;另外，H越接近1，时间序列的持续程度越强，反之越弱［19］。

2.2.2 时间序列的循环周期。引入统计量V(n)，以定量描述时间序列的平均循环周期:

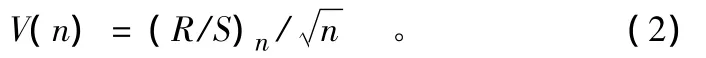
V(n)可用于检验R/S分析的稳定性，更重要的是可以很好地确定时间序列是否存在周期循环并估计周期长度。对于独立随机过程的序列而言，统计量V(n)-lg n曲线接近平坦;而对于具有状态持续性(H ＞0.5)的时间序列，V(n)-lg n曲线向上倾斜;反之，对于具有逆状态持续性(H ＜0.5)的时间序列，V(n)-lg n曲线向下倾斜。如果V(n)-lg n曲线上V(n)随lg n的变化趋势发生变化，即曲线出现明显转折时，说明历史状态对未来状态的影响消失，此时系统的平均循环周期T就是对应的时间跨度n。T表征了系统对初始条件的平均记忆长度，即系统通常在多长时间后完全失去对初始条件的依赖。

2.3 灰色系统GM(1，1)模型

2.3.1 模型的建立。设原始序列为:

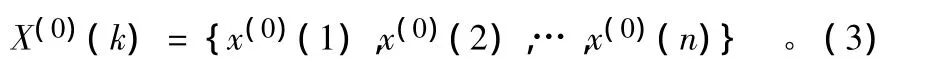
对X(0)(K)作一次累加，得到:

1)模型的微分方程为:

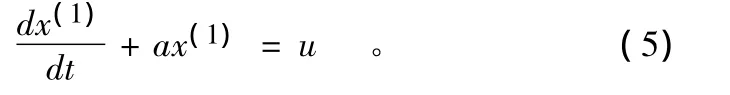
2.3.2 模型的求解。将时间响应函数离散化，利用初始条件对(5)求解，得:

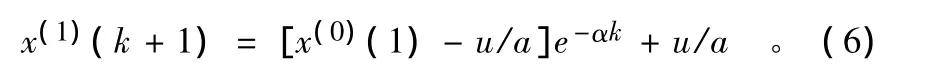
经累减还原可得原数据序列的估计值:

2.3.3 模型精度和适用范围。灰色预测模型一般有残差检验、关联度检验和后验差检验3种方法。其中，残差检验是对实测值和预测值之间的误差进行逐点检验的方法，通过各点的相对残差值，可以计算出预测模型的精度值P。设实测序列为式(3)所示，预测序列为:

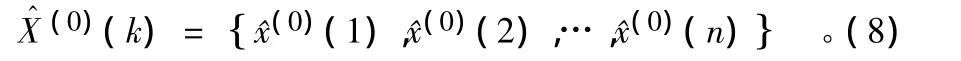
则平均相对误差为:

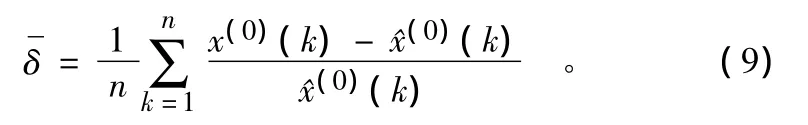
精度为:

若P≥0.8，模型通过残差检验;若P ＜0.8，则须对模型进行修正，使之满足对精度的要求(P≥0.8)，才可以进行预测。精度越高，说明模型拟合得越好。

3 结果与讨论

3.1 径流量的R/S 分析

利用上述模型，对1949—2011年黑河上游莺落峡水文站测流断面年径流量(即黑河出山径流量)序列(图2)进行R/S分析。由于R/S分析要对序列进行等额分组，为了便于分组，取1949—2008年(共60年)的径流量为R/S分析对象;取2009—2011年的径流量作为对比值。

图2 黑河出山年径流量变化曲线Fig.2 Annual runoff curve at Yingluoxia Station

3.1.1 Hurst指数。分别取 n 为 3，5，6，10，12，20，30，对径流量序列进行分析计算，并做出lg n与lg(R/S)拟合图(图3)。

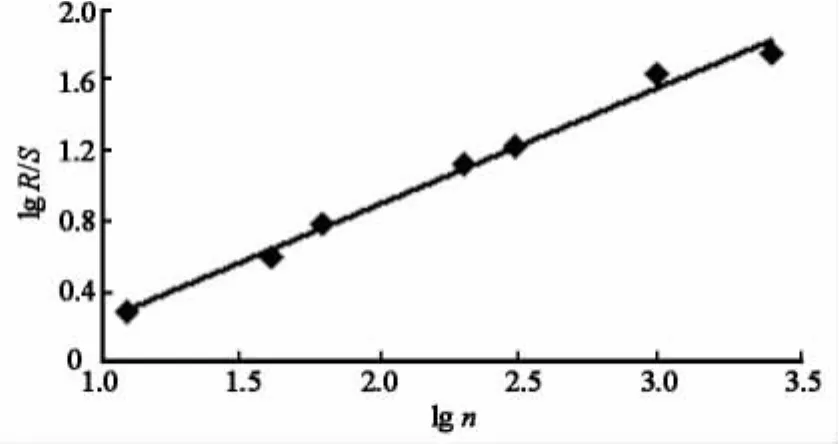
图3 黑河出山年径流量R/S分析Fig.3 R/S analysis of annual runoff at Yingluoxia Station

由图3可得:lg R/S=0.665 8，lg n-0.431 2，R2=0.991。所以，黑河出山径流量序列的 Hurst指数为0.665 8。H大于0.5，说明黑河出山年径流量序列为分形时间序列，存在长期记忆性和持续性。

3.1.2 平均循环周期。根据式(2)计算统计量V(n)，并绘制V(n)-lg n数据点折线图(图4)。

由图4可知:①黑河出山径流量V统计量的曲线呈上升趋势。这进一步说明序列中存在长期记忆，这种持久性是内在的，是径流过程复杂性所反映的事实。② 曲线的拐点可以确定曲线出现明显转折的位置，拐点横坐标所对应的时间点即为系统的平均循环周期。黑河出山径流序列在n=20时(箭头所示处)出现一个突变点，说明该序列的平均循环周期T=20。T表征了系统对初始条件的平均记忆长度，即黑河出山径流量序列在20年后将完全失去对初始条件的依赖。

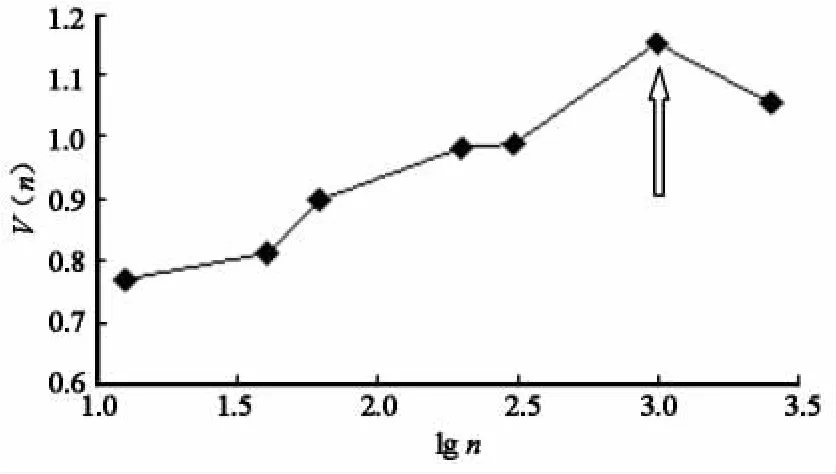
图4 黑河出山年径流量V(n)-lg n统计Fig.4 V(n)-lg n chart of annual runoff at Yingluoxia Station

3.2 径流量R/S灰色预测

由R/S分析可知，黑河出山径流量序列的平均记忆期为20年，即第k年径流量的值会影响到第(k+19)年的径流量，而对再往后的径流量影响甚弱，甚至没有影响。所以，可采用以下方法进行黑河出山径流量的灰色预测(以预测2009—2011年水文径流量为例)。

①取1990—2008(共19年)的径流量作为初始值，预测初值序列的径流量，并对预测模型进行验证。②如果预测模型精度大于80%，则用1990—2008年的径流量预测2009年的径流量。③ 取1991—2008年的径流量以及2009年预测值作为初始值，预测2010年的径流量。④取1992—2008年的径流量以及2009，2010年的预测值作为初始值，预测2011年的径流量。预测过程采用式(3)～(7)计算。验证过程采用式(8)～(10)计算。

经计算，模型的平均误差为10.31%，预测精度达到了89.69%。所以，以1990—2008年的径流量作为测模型的初值是可行的。其预测结果见表1。

表1表明，2009—2011年的预测值与实际值的平均相对误差为8.96%，预测精度达到了91.04%。说明在R/S分析之后利用灰色理论进行涌水量预测方法可行。

表1 2009—2011年黑河出山径流量预测值与实际值比较Tab.1 Comparison between predicted and measured values of annual runoff from 2009 to 2011 at Yingluoxia Station

3.3 讨论

3.3.1 与直接进行灰色预测比较。将1949—2008年的全部数据作为预测模型的基础数据以预测2009—2011年的径流量，计算结果与基于R/S分析后的灰色预测结果进行对比(表2)。由表2可知，直接进行灰色预测与基于R/S分析的灰色预测的精度分别为90.42%和91.04%，后者稍高一些。说明在R/S分析之后，只要20年的径流量资料就可以进行径流量灰色预测，且预测结果的精度要高于直接采用灰色预测的精度。

表2 不同预测方法的出山径流量预测结果比较Tab.2 Comparison of annual runoff at Yingluoxia Station by different forecasting methods

在本研究中，R/S灰色预测方法的优势不明显，只比直接进行灰色预测的结果稍好。原因在于黑河出山径流序列(1949—2008年)的随机波动性小，适合直接进行灰色预测;但是对于随机波动性大的长时间序列，直接进行灰色预测几乎是不可能的，此时R/S灰色预测的优势就十分明显。所以整体而言，R/S灰色预测法是进行时间序列预测新的、有效的方法。

3.3.2 关于周期T。根据莺落峡断面1949—2008年径流量，采用R/S分析得到的黑河出山径流量循环周期为20年;侯红雨、杨丽丰等根据莺落峡断面1945—2007年径流量采用周期均值叠加法得到的黑河出山径流量循环周期为22年［2］;王钧、蒙吉军根据莺落峡断面1944—2005年平均流量利用小波分析得到莺落峡流量变化在60年尺度的最大周期为25年［20］。分别取T=20，22，25，采用前文中①～④的步骤进行R/S灰色预测，得到如下预测结果(表3)。

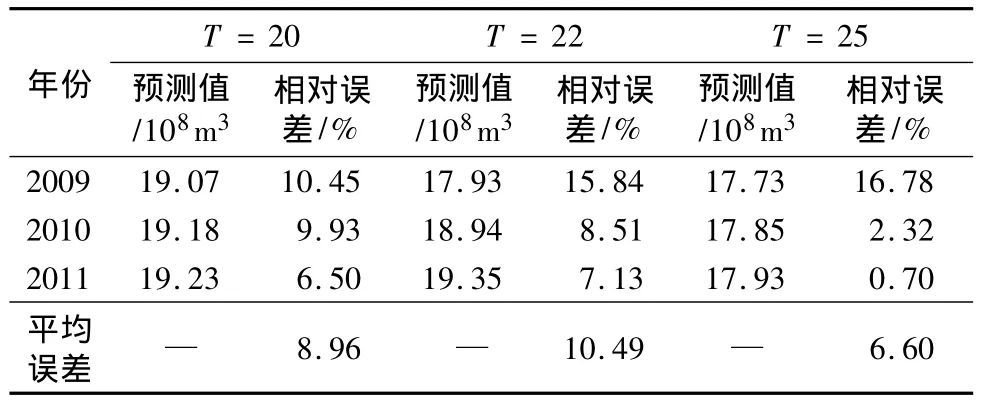
表3 不同周期下黑河出山径流量R/S灰色预测结果比较Tab.3 Comparison of annual runoff by R/S gray predicted under different cycles at Yingluoxia Station

由表3可知:① 不同周期下的预测精度分别达到91.04%，89.51%和93.4%;T取20年和25年时，利用灰色预测所得结果的精度都在90%以上。由于测流断面相同，径流量序列也基本一致，所以可以认为黑河出山径流量循环周期应该在20～25年之间。②3个不同的周期是利用不同方法求出的结果;在求出周期T之后，可以再利用灰色预测方法进行径流量的预测，且预测精度都比较高，说明灰色预测与其他方法结合预测效果更好。

4 结论

1)径流量时间序列具有分形特征，可利用R/S方法进行分析，Hurst指数H和平均循环周期T是R/S分析法稳定有效的统计量。H可以判定径流量时间序列的分形结构和状态持续性;T用于检验R/S稳定性，判别序列是否存在周期循环及估计周期长度。径流量序列也具有明显的灰色特征，基于R/S分析的灰色预测模型为径流量预测提供了一种新的方法。

2)黑河出山径流量序列(1949—2011年)具有明显的状态持续性，其循环周期在20～25年之间，在进行R/S灰色预测时，取T=20为宜，预测精度为91.04%。

3)在我国，分形理论应用于径流过程研究已经有十多年的时间，但目前仍然处在验证阶段。这与分形是一门新的学科、其基础理论的研究还不完善有很大的关系。如何进行深入研究，是各学科面临的共同问题。就径流过程而言，应该从分形的基础理论和径流变化机理2个方面做进一步的深入探索。

4)本研究在利用R/S法分析径流量序列的变化趋势和周期后，只采用了灰色预测方法对黑河出山径流量进行了预测和对比分析。是否可以将R/S分析方法和其他方法结合进行径流量预测，将做进一步的探讨;另外，不同分析方法可以与灰色预测相结合进行径流预测，也将在以后做进一步的研究。

［1］吴维臻，李金麟，田杰，等.黑河流域出山径流模拟［J］.干旱区资源与环境，2013，27(8):143-147.

［2］侯红雨，杨丽丰，李福生，等.基于时间序列分析的黑河干流年径流预报［J］.人民黄河，2010，32(12):49-51.

［3］杨明金，张勃.黑河莺落峡站径流变化的影响因素分析［J］.地理科学进展，2010，29(2):166-172.

［4］陈仁升，康尔泗，杨建平，等.黑河出山径流的非线性特征分析［J］.冰川冻土，2007，24(3):292-298.

［5］刘起方，马光文，刘群英，等.基于分形插值理论的径流预测探讨［J］.水力发电学报，2008，27(4):20-25.

［6］李建林，张洪云，冯有利，等.煤矿断层构造复杂程度的非线性分析［J］.中国地质灾害与防治学报，2011，22(4):69-73.

［7］谢平，陈广才，雷红富.基于Hurst系数的水文变异分析方法［J］.应用基础与工程科学学报，2009，17(1):32-39.

［8］门宝辉，刘昌明，夏军，等.R/S分析法在南水北调西线一期工程调水河流径流趋势预测中的应用［J］.冰川冻土，2005，27(4):568-573.

［9］王孝礼，胡宝清，夏军.水文时序趋势与变异点的R/S分析［J］.武汉大学学报(工学版)，2002，35(2):10-12.

［10］汪秉仁，邓琦.灰色系统理论在水文研究中的应用［J］.中原地理研究，1985，4(1):11-22.

［11］蓝永超，杨志怀，权建民，等.灰色预测模型在径流长期预报中的应用［J］.中国沙漠，1997，17(1):49-52.

［12］吴丽娜，黄领梅，沈冰.大峪河年径流量的灰色拓扑预测与趋势分析［J］.人民黄河，2012，34(1):62-65.

［13］马建琴，许龙宾，师琨.改进型灰色马尔科夫模型在径流预测中的应用［J］.华北水利水电学院学报，2012，33(2):39-42.

［14］李旭谱，张福平，魏永芬.黑河流域植被覆盖程度变化研究［J］.地域研究与开发，2013，32(3):108-114.

［15］楚永伟，蓝永超，李向阳，等.黑河莺落峡站年径流长期预报模型研究［J］.中国沙漠，2005，25(6):869-873.

［16］徐中民.黑河流域水资源管理方式的初步探讨［J］.地域研究与开发，2000，19(1):17-20.

［17］党素珍，刘昌明，王中根，等.黑河流域上游融雪径流时间变化特征及成因分析［J］.冰川冻土，2012，34(2):920-926.

［18］燕爱玲，黄强，刘招，等.R/S法的径流时序复杂特性研究［J］.应用科学学报，2007，25(2):214-217.

［19］陈正华，陈植华，张溪，等.R/S分析方法在矿井涌水量变化预测方面的应用［J］.矿业安全与环保，2010，37(1):36-38.

［20］王钧，蒙吉军.黑河流域近60年来径流量变化及影响因素［J］. 地理科学，2008，28(1):83-88.