运用非均匀三次B样条拟合我国国债利率期限结构
戴习民, 朱晓临, 张仁琼
(1.合肥工业大学数学学院,合肥230009; 2.合肥工业大学图书馆,合肥230009)
1 引 言
利率期限结构是指不同期限的利率与期限之间的函数关系.刻画利率期限结构的主要工具是无风险收益率曲线,它是一条以时间为横坐标,以各时间点对应的无风险利率为纵坐标的曲线,也称作零息利率曲线、收益率曲线.和零息利率等价的刻画利率期限结构的工具是贴现函数和瞬时远期利率,这三者之间可以互推.在经济活动中,零息利率是基准利率,发挥着基础性地位的重要作用. 但由于市场上金融产品的种类有限,不能直接观察到所有期限的无风险利率水平,因此只能依靠市场有限的金融产品,通过建立数学模型来建立整个期限上的利率期限结构.考虑到对无风险的要求,通常选取各国以国家信用为担保的国债作为无风险债券.
在对利率曲线结构的建模研究中,一种常见的类型就是静态模型法.这种方法根据市场上已有的国债价格数据,从中获取有限个时点上的利率期限结构的信息,再通过插值、拟合等数值方法来获取整个期限上的利率期限结构.发展最丰富、应用最广泛的的就是基于广义样条函数的拟合模型,根据所使用的样条函数种类可分为多项式样条模型、指数样条模型、B样条模型以及平滑样条模型、Hermite插值模型等.其中三次B样条函数因其功能强大、简洁易用的特点而被广泛应用.
McCulloch(1971,1975)[1,2]最早将多项式样条函数应用于利率期限结构的估计,该方法假设贴现函数为分段连续的多项式函数,通过多元线性回归估计每段多项式的系数,从而构建贴现函数;Vasicek和Fong(1982)[3]运用的是指数样条函数;Steeley(1991)[4]首先引入了B样条模型;Deacon和Derry(1994)[5]通过比较各种方法后认为三次B样条模型在实践中具有最好的效果;Marico和Marcelo(2010)[6]运用了约束光滑B样条(CBOS)法.在国内,杨春鹏和曹兴华(2002)[7]利用回归插补法和三次样条插值法来构造我国的国债到期收益率曲线;朱峰(2003)[8]对三次B样条模型和Svensson(1995)[9]模型对于我国国债收益率曲线的拟合效果进行比较研究发现,Svensson模型的拟合精度较好,而三次B样条模型则在拟合效果的稳定性上占优;刘灿和易璐(2004)[10]则利用B样条函数法实证研究了我国深沪两市国债收益率的期限结构.
在确定B样条函数的节点向量时,多数文献采用了Mcculloch建议的原则,即样条的段数约等于样本数量的平方根,而节点的选择应使得剩余期限落在每段样条区间里面的债券的数目大致相等,且取的节点都是整数值节点.我们称这种方法为“等额债券数目法”.在这种方法指导下,国内关于我国国债利率期限结构的研究文献,大都将样条的段数取为3,需要四个不同的内节点.在考虑我国债券的实际期限的基础上对此方法作微小变化调整的还有如下类型:闵晓平、田澎(2006)[11]将内节点设置为固定的{0,5,7,20};刘灿和易璐(2004)[10]则使用了等距节点法,所取的内节点为{0,7,14,20};朱世武、陈健恒(2003)[12]考虑使得每个分段函数中相应的国债数量要保持平均以及为了利率曲线的平滑过渡,所取的内节点为{0,5,8,20}.
以上这些节点位置的取法,一方面没有考虑到有现金流量产生的时间点对决定利率期限结构的意义,另一方面,也没有考虑到现金流量的大小对利率期限结构的影响.但正是债券的现金流的时间点和现金流的大小从本质上决定了利率的期限结构,因此在构建利率期限结构模型时,应该在模型中尽快的能将这两项指标融合到模型的变量选取和关系设置中去,这样才更符合具体的实际经济含义.基于这种角度考虑,本文采用了一种新的节点向量确定方法,即“等额现金流量法”.这种方法以产生现金流的时间点为节点,以使得各样条区间段内的现金流量尽可能相等为标准,来确定样条的节点位置.实证研究的结果显示,这种方法拟合的利率期限结构的形状比较符合经济原理,而且对债券价格的估计误差要比“等额债券数目法”极其衍生的几个方法有优势.
2 模型的理论分析
假定起始时刻为0,记未来t时刻的贴现函数值为δ(t),与之相应的零息票收益率曲线为r(t)、瞬时远期利率曲线为f(t),这三者之间满足如下关系式:
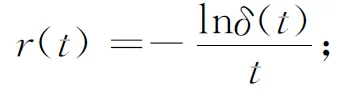
(1)
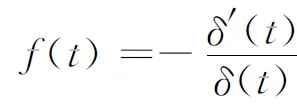
(2)
假设国债市场所蕴含的贴现函数为δ(t),对第l只附息债券. 如果它在将来的Nl个时刻tj(j=1,…,Nl),分别支付数量为C(tj)的现金流,那么它在当前时点的价格Pl应为
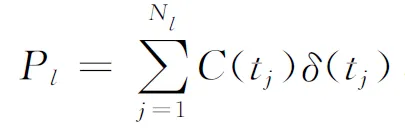
(3)
其中l=1,…,M,M为债券数目.
本文选择用三段三次B样条曲线来拟合贴现函数.因此,要选定四个不同的内节点,连同首末节点,总共需要给定八个节点.记节点向量为
knots={t0,t1,t2,t3,t4,t5,t6,t7},
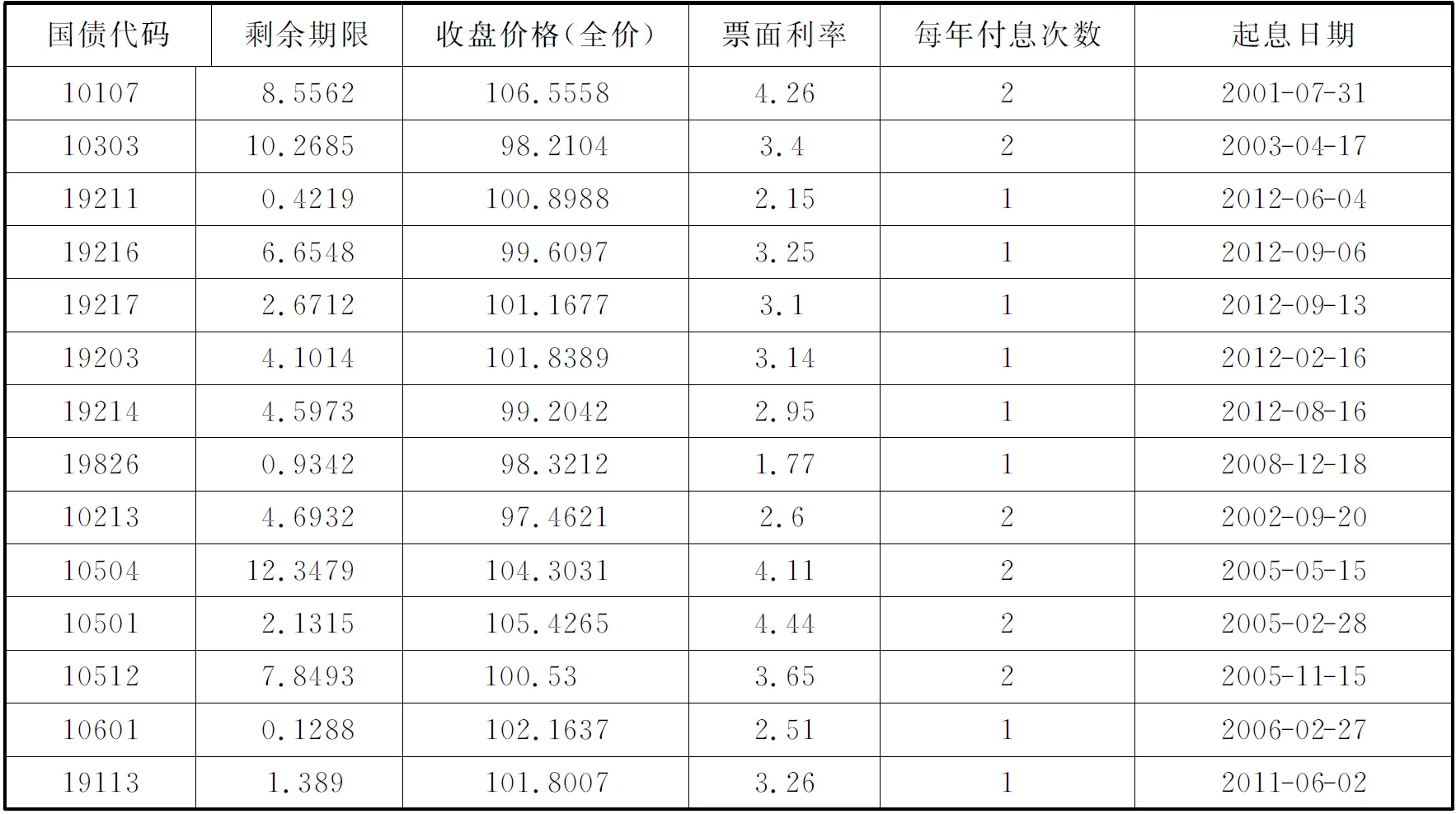
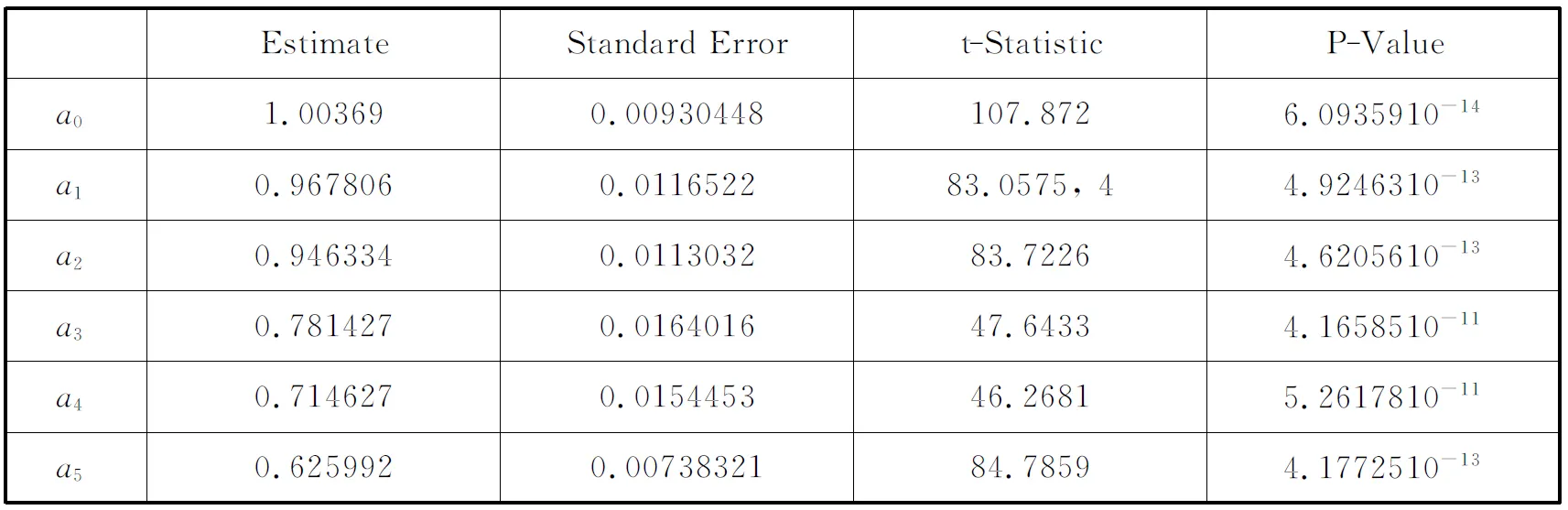
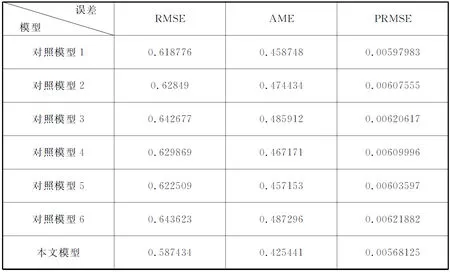
其中t2 knots={0,0,0,t3,t4,T,T,T}, 其中0表示把取得样本债券的日期当成起始时刻,记为0时,T为样本债券中剩余期限的最大值. 在内节点位置的选择上,我们采用一种新的“等额现金流量法”.具体做法如下.首先根据选择的样本数据,计算出样本中每种国债的付息时间点,所有这些时间点(包括每种国债的到期日,在该日债券将支付票面价值和最后一次利息)都将作为节点的候选点;其次,计算出这组债券在整个时间段[0,T]上的现金流的总和,其中T是所有债券剩余期限的最大值;最后从候选点中确定出t3和t4,使分别落在区间[0,t3],(t3,t4]和(t4,T]上的现金流量大致相等.称这种决定样条节点向量的方法为“等额现金流量法”. 记以上节点决定的六个三次B样条基函数为 关于B样条基函数的de-Boor Cox 算法,请参见[13,14],本文不再赘述. 记贴现函数δ(t)的拟合函数为,用三次B样条函数来拟合贴现函数 (4) 其中ai为待定系数,也称曲线的控制顶点. (5) 由于估计价格与实际价格存在一定的误差,记 其中Pl为市场价格. 因此模型的目标函数设为 (6) 即求得ai,i=0,…,5,使得拟合的债券价格与实际价格的误差平方和最小.实现以上目标的过程,运用普通最小二乘线性回归(OLSR)即可实现. 本节选取2013年1月11日上海证券交易所的记账式国债交易数据进行实证研究(在2013年内,当日有交易量的债券数目较大).剔除交易量为零、浮动利息及发行价不等于100的债券,剩余的14只国债作为样本数据,样本数据见表1.数据来源:Wind金融资讯. 计算了以上14只债券未来所有的付息日和到期日这些时间点,以及这些时间点上的现金流.其中最长剩余期限为12.35年,所有时间点上的现金流总和为1652.03元,根据在前节描述的等额现金流法的节点决定方法,最终选取的节点向量为 knots={0,0,0,2.13,4.70,12.35,12.35,12.35}, 其中在区间[0,2.13]上的现金流量和为588.11元,在区间(2.13,4.70]上的现金流量和为474.33元,在区间(4.70,12.35]上的现金流量和为589.59元. 模型拟合结果如下: 1.拟合的系数ai,i=0,…,5为 {1.00369, 0.967806, 0.946334, 0.781427, 0.714627, 0.625992}. 表1 样本数据 2.拟合模型的总体检验. 表2 模型的各系数的检验 模型总体拟合优度R2=0.999966; AdjustedR2=0.999941. 由上可知,模型的拟合优度很高,各系数都高度显著,说明模型的设置是合理的,能充分拟合样本数据. {1.51365, -0.907492, 0.256758, 0.222955, -0.124293, -0.396907, -0.151851, -0.27091, 0.00951531, 0.203761, 0.720245, -0.834808, -0.084174, -0.258854}. 4.模型拟合的贴现函数、收益曲线、瞬时远期利率曲线的图像见图1. (a) 贴现函数 (b)收益率曲线 (c)瞬时远期利率曲线图1 利率期限结构的三个函数图像 根据以上的结果可知,模型估计的贴现函数在0时的值几乎等于1,符合现实的经济意义.贴现函数图像呈现平稳的单调递减形状,与经济学中货币的时间价值理论符合.估计的收益率曲线显示,2013年1月11日,我国国债市场蕴含的1年期左右的短期收益率偏高.但2年期及2年期以上的中长期收益率呈平稳上升趋势,符合利率假说的流动性偏好理论,也与我国资本市场的实际利率情况相符.瞬时远期利率曲线也显示市场预期未来2年以内的短期收益率偏高,将有下降趋势,未来2年后至至5年内间的利率将显著上升,而未来5年以后的利率将有先小幅下降再上升的趋势. 本节将本文采取的“等额现金流量法”与“等额债券数目法”及其衍生模型作比较,绘制了每一种模型的三种表示利率期限结构的函数的图像,并给出了每种模型对债券价格估计的三种误差. 首先对表1所提供的数据,采用上述的“等额债券数目法”来决定节点向量,产生了三个对照模型1,2,3,用内节点为{0,5,7,20}产生对照模型4,用内节点为{0,5,8,20}产生对照模型5,用内节点为{0,7,14,20}产生对照模型6.所有模型拟合的利率期限结构图像限于篇幅不在此一一列出.所有模型对债券价格的拟合误差统一在表3中. 为了模型之间比较时在整个时间区间上的统一性,统一取所有模型中的T=20.误差计算方法我们选用了常用的三种: 均方根误差RMSE: (7) 平均绝对误差MAE: (8) 百分比均方根误差PRMSE: (9) 误差计算结果如表3. 表3 本文模型对债券价格的估计误差 从拟合的利率期限结构图形来看,本文模型拟合的三条曲线也比较合理,基本符合实际经济含义,不足之处在于远期瞬时利率曲线在末端点处有一定程度的偏离现象.对照模型4,5,6的收益率曲线在近端点的图形不符合实际经济意义,对照模型6的收益率曲线和瞬时远期利率曲线都不符合实际经济含义,模型效果不佳. 对照模型5的三种图形都很异常,而且所有对照模型在末端都有一定程度的偏离现象.而根据表3提供的对债券价格的拟合误差来看,在三种误差指标中,本文模型都是最小的.综上可知,本文所采用的“等额现金流量法”来确定样条节点的技术是一种更好的选择. 另外,我们还进行了模型的稳健性测试,采用了其他随机抽取的交易日的数据,将本文模型和其他六种模型做比较,结果显示,本文模型在不同的样本数据情况下,表现稳定,拟合的利率期限结构基本符合现实情况,没有出现剧烈的变动.在对债券价格的估计误差上,本文模型在债券数目较多时占显著优势,在债券数目较少时,本文模型处于中间水平.综合两方面情况,显示本文模型是一个较好的选择. 本文采用“等额现金流量法”来确定样条节点向量,将债券的两个本质要素,附息时间点和现金流量大小结合到了模型中去,使得模型和实际经济情况更密切结合,更能揭示债券价格所蕴含的利率期限结构.将本文模型的结果与采用“等额债券数目法”模型的三种结果、固定节点向量的三种模型结果统一作了比较.实证研究结果显示,我们的方法在表示利率期限结构的三种函数图像上均具有良好的表现,总体上基本符合理论经济假说和实际经济情况.而对照的六种模型,三种函数的图像都不同程度的出现了不符合实际经济情况的现象. 在对债券价格的估计误差上,本文模型在债券数目越多时越能体现出其优势.造成这种现象的重要原因是样本数据中债券数量的减少,使得总体时间上现金流时间点和现金流量都减少,从而提供的有实际意义的信息量减少,因而降低了本文模型的拟合效果.我国债券市场发展程度不够,发行的债券数目总体较少,每个交易日有交易量的债券数目更少,因此使得本文模型的优势在实证研究中没有充分体现.如果借助债券市场发达国家的数据,在更多的债券价格作为样本的情况下,可能会更好的体现我们模型的优势,这方面的实证研究还有待下一步工作来进行. [参 考 文 献] [1] McCulloch J H. Measuring the term structure of interest rates[J]. Journal of Business, 1971,44(1):19-31. [2] McCulloch J H. The tax adjusted yield curve[J]. Journal of Finance, 1975, 30: 811-830. [3] Vasicek O A, Fang H G. Term structure modeling using exponential Splines[J].The Journal of Finanece,1982, 37(2):339-356. [4] Steeley J M. Estimating the gilt-edgsed term structure: basis Splines and confidence intervals[J]. Journal of Business Finance and Accounting, 1991,18(4):513-29. [5] Deacon M, Derry A. Estimating the term structure of interest rates[R]. London: Bank of England, 1994. [6] Marcio P L, Mrcelo M. Constrained smoothing B-splines for the term structure of interest rates[J].Insuarance:Mathematics and Economics, 2010,46:339-350. [7] 杨春鹏,曹兴华. 我国国债收益率曲线的构造与实证研究[J]. 投资与证券, 2002, 10:24-28. [8] 朱峰. 国债即期收益率曲线的拟合估计[J]. 证券市场导报, 2003, 4:31-36. [9] Svensson L E O. Estimating forward interest rates with the extended Nelson & Siegel method. Quarterly Review, Sveriges Riksbank, 1995, 3:13-26. [10] 刘灿,易璐. 深沪两市国债收益率期限结构的实证研究[J]. 证券市场导报, 2004, 2:36-41. [11] 闵晓平, 田澎. 基于B样条函数的上交所利率期限结构估计[J]. 管理工程学报,2006,20(4):77-81. [12] 朱世武, 陈健恒.交易所国债利率期限结构实证研究[J]. 金融研究,2003,10:63-73. [13] 施法中. 计算机辅助几何设计与非均匀有理B样条(CAGD& NURBS)[M].北京, 高等教育出版社, 2001. [14] Farin G. Curves and surfaces in computer aided geometric design[M]. 5th ed. San Francisco: Morgan Kaufmann, 2001.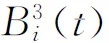
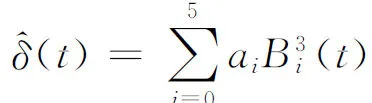
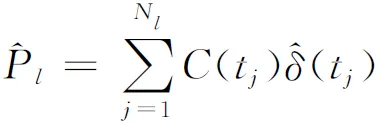
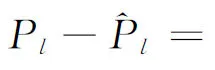
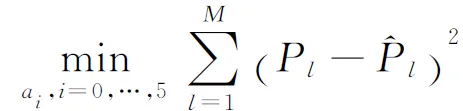
3 模型的实证研究

4 与其他模型的比较
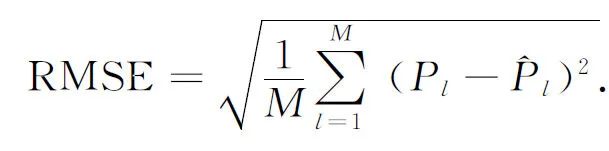
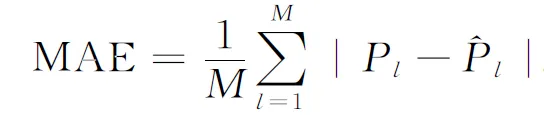
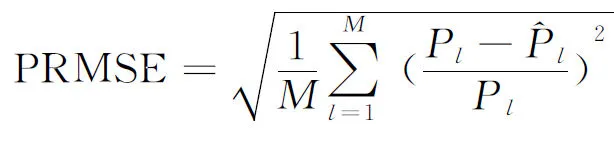
5 结 论

