Hermite插值算子在Orlicz空间内的逼近
吴晓红, 吴嘎日迪
(1. 呼和浩特民族学院数学系,内蒙古呼和浩特市010051;
2.内蒙古师范大学数学科学学院,内蒙古呼和浩特市010022)
1 引 言


其中


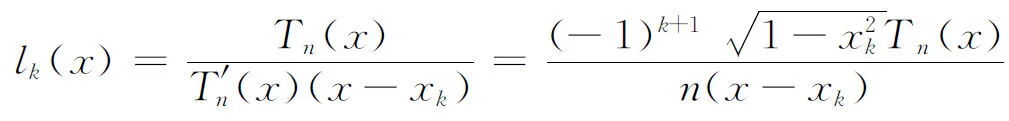
然而在文献[2]中作者讨论了Hn(f,x)在加权LP(p>0) 范数下的逼近性质,得到了逼近定理A:
定理A[2]设f∈C′[-1,1],p>0,α>-1,则有

本文为了讨论该算子在Orlicz 空间内的逼近性质,把它转换为Kantorovich 型算子,即



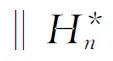
‖·‖M=‖·‖M([-1,1])为由N-函数M(u)生成的Orlicz范数,即

关于N-函数的定义及性质请看文献[3].
定义


为r阶差分

则ωr(f,t)M满足如下性质:
(i)ωr(f,t)M是关于t的单调递增函数且ωr(f,0)M=0;



本文用C表示一个绝对常数,在不同处可表示不同的值.
2 辅助引理

证利用

直接可得
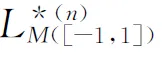


‖M(f,x)‖M≤C‖f‖M,

3 定理的证明


=∶I1+I2+I3,
利用Hölder不等式和引理1,有

再利用引理2,得



综上所述,得



再次利用引理2,得

[参考文献]:
[1] 谢庭藩,周颂平.实函数逼近论[M].浙江:杭州大学出版社,1998.
[2] 齐宗会,许贵桥.Hermite插值算子在LP范数下的逼近[J].天津师范大学学报,2009,29(3):4-7.
[3] 吴丛炘,王廷铺.奥尔里奇空间及其应用[M].哈尔滨:黑龙江科学技术出版社,1983.
[4] Wu Garidi. On approximation by polynomials in Orlicz spaces[J].Approximation theory and its application,1991,7(3):97-110.
[5] 吴晓红,吴嘎日迪.Bernstain-kantorovich算子在Orlicz空间内的逼近[J].内蒙古师范大学学报,2010,39(6):569-572.

