油池火灾火焰高度关系模型的准确度研究

李姗姗，孙建刚，王 振，王楠楠，崔利富

(大连民族学院土木建筑工程学院，辽宁大连116605)

池火灾是指可燃液体泄漏后流到地面形成液池，或流到水面并覆盖水面遇到点火源而形成的火灾［1］。在不同类型的火灾中，池火灾最为常见。由于热流量非常高，如果火焰直接接触到设备表面，会使设备产生损坏。当池子直径大于1 m时，池火灾的破坏作用主要体现在对邻近人员及设备的热辐射影响上，使附近的人员受到伤害并可引燃周围的可燃物，从而造成重大的损失［1-2］。池火灾火焰高度决定了火焰表面热流量、火焰热辐射强度及火灾持续的时间，进而决定了火灾的危险程度及其影响的范围，因此池火灾火焰高度的合理预测对预防及控制池火灾事故的发生，减少事故造成的人员伤亡、财产损失等方面具有重要的现实意义。目前对于池火灾火焰高度的理论研究集中于CFD软件模拟及关系模型计算两种方法上［3］。软件模拟考虑的影响因素较多、准确性较高，但是软件操作复杂，计算量非常大;关系模型采用经验公式计算，考虑的影响因素相对较少，但是其计算简单、便捷，如果能够明确其计算的准确性，将其应用于工程项目中将大大缩短理论计算时间。

本文为了对大庆油田原油储罐池火灾火焰形态及危害情况加以分析，开展了池火灾关系模型用于计算原油池火灾火焰高度时的准确度研究。对不同直径原油池火灾火焰高度进行了实验测试，并将测试结果与池火灾关系模型计算结果进行了比较，最后基于实验结果对Thomas关系模型进行了修正。

1 实验系统简介

实验采用大庆油田原油，实验系统由圆盘、燃烧池及保护网组成。圆盘直径分别为1.5，2，3和5 m，圆盘深度为0.15 m，罐底部水垫层的厚度为50 mm，油层漂浮在水面高度100 mm。实验中将圆盘放于燃烧池中心，燃烧池外围设置保护网以确保实验的安全，保护网采用钢骨架内焊接2 mm厚冲孔钢板网，钢结构骨架采用L70×70×8角钢，焊接链接，柱下设置C15混凝土基础，角钢柱插入基础。实验燃烧池及外围保护网示意图如图1，油池火灾保护网结构平面布置图如图2。

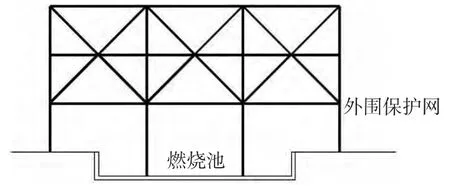
图1 油池火灾实验燃烧池及外围保护网示意图

图2 油池火灾保护网结构平面布置图

实验记录环境温度、风速和风向等气象参数。在圆盘底部引出U型管，刻上刻度，并由摄像系统记录U型管的刻度，由此来计算竖向燃烧速度。该值将作为后续池火灾火焰高度理论计算的输入值，实验方案如图3。实验利用摄像机及红外成像系统记录火焰图像如图4，通过记录的火焰图像测量得到火焰高度。

图3 圆盘池火灾实验系统示意图

图4 池火灾火焰图像

2 火焰高度实验测试结果

根据SFPE的定义，火焰高度定义为火焰锋线与燃烧表面之间的垂直距离［4］。1.5 m直径池火灾点火后900～960 s时间内火焰瞬时高度实验测试值如图5;池火灾火焰高度的测试在室外进行，测试时间内的平均风速为0.9 m·s-1，最大风速1.3 m·s-1。2 m直径池火灾点火后500～560 s时间内火焰瞬时高度实验测试值如图6;上述测试时间内的平均风速为0.4 m·s-1，最大风速为1.3 m·s-1。3 m直径池火灾点火后440～500 s时间内火焰瞬时高度实验测试值如图7;测试时间内平均风速为0.4 m·s-1，最大风速为0.4 m·s-1，风速较小且较为平稳。5 m直径池火灾点火后500～560 s时间内火焰瞬时高度实验测试值如图8;测试时间内的平均风速为0 m·s-1，最大风速为0.4 m·s-1。本文取60 s时间内的瞬时火焰高度的算术平均值作为平均火焰高度，这样计算平均火焰高度较为简单，而且准确度相对较高。从图5-图8中清楚可见火焰燃烧过程中的脉动和跳跃现象，1.5 m直径油池池火灾火焰平均高度为2.34 m，2 m直径油池池火灾火焰平均高度为3.01 m，3 m直径油池池火灾火焰平均高度为7.88 m，5 m直径油池池火灾火焰平均高度为9.31 m。

图5 1.5 m直径油池火灾火焰高度实验测试值

图6 2 m直径油池火灾火焰高度实验测试值

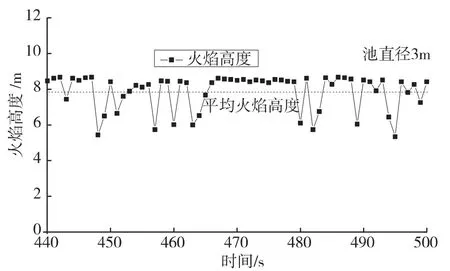
图7 3 m直径油池火灾火焰高度实验测试值

图8 5 m直径油池火灾火焰高度实验测试值

3 火焰高度关系模型的准确度研究

池火灾火焰高度的关系模型是基于实验数据及量纲分析等所得到的经验公式，应用较多的是Thomas关系模型和Heskestad关系模型。Thomas［5］基于实验以及量纲分析，得到了湍流火焰平均高度的关系模型，计算式为

式中，H为火焰高度，m;D为池直径，m;m'为燃料燃烧速率，kg·(m2·s)-1，ρ0为空气密度，取为1.293 kg·m-3;u为10 m处风速，m·s-1;uc为特征风速

Heskestad［6］对广泛的实验数据进行数学处理，得到了下面的火焰高度公式:

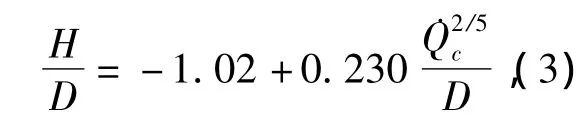
式中，˙Qc为热释放速率，˙Qc=0.25×3.14×D2×η×Hc×m';η为燃烧效率;Hc为燃料燃烧热，原油燃烧热43 890 kJ·kg-1。

将不同池直径下火焰高度的实验测试值与上述Thomas和Heskestad关系模型的理论计算结果进行了比较。实验值与关系模型理论计算值的比较图如图9，理论计算公式中风速值取实验平均风速，理论计算公式中的燃料燃烧速度采用实验测试值。从图9可见，对于不同直径池火灾，Heskestad经验公式理论计算值与实验测试值相比偏差较大。在池直径为1.5 m和2 m时，Thomas关系模型火焰高度理论计算值与实验值较为接近;在池直径为3 m和5 m时，Thomas关系模型火焰高度理论计算值小于实验值且偏差较大。

图9 池火灾火焰高度实验测试值与理论计算值比较图

4 火焰高度关系模型的修正

系模型理论计算值的比，图中实心点分别为池直径1.5 m、2 m、3 m及5 m时火焰高度测试值与Thomas关系模型理论值的比，可见火焰高度实验值与Thomas关系模型理论值的比与油池直径的自然对数值可拟合成线性曲线，由此得到如下修正后的公式:

图10 火焰高度实验值与理论值的比与池直径对数的关系

上述公式的修正是基于池直径1.5，2，3和5 m的原油池火灾火焰高度实验值开展的，在池直径小于5 m时修正公式具有更高的准确度，但是其在原油池直径大于5 m时其准确度还有待进一步研究。

5 结论

为了对大庆油田原油储罐池火灾火焰形态及危害情况加以分析，开展了池火灾关系模型用于计算原油池火灾火焰高度时的准确度研究。搭建了火焰高度实验测试系统对大庆油田原油池火灾在不同池直径下的火焰高度进行测试，并将测试结果与应用较多的Thomas关系模型和Heskestad关系模型计算结果进行比较。结果表明:Thomas关系模型计算准确度高于Heskestad关系模型;在池直径为1.5 m和2 m时，Thomas关系模型火焰高度理论计算值与实验值较为接近;在池直径为3 m和5 m时，火焰高度实验值约为Thomas关系模型理论计算值的2倍，两者偏差较大。由于上述关系模型不是基于原油池火灾火焰高度实验结果分析所得到的经验公式，故应用于原油池火灾火焰高度计算时会存在一定的偏差。在此基于原油池火灾火焰高度实验结果对准确度相对较高的Thomas关系模型进行了修正，通过对于实验数据的分析发现，火焰高度实验值与Thomas关系模型理论值的比与油池直径的自然对数值可拟合成线性曲线，拟合后得到了修正的Thomas关系模型。修正后的模型在池直径小于5 m时其具有更高的准确度，但是其在原油池直径大于5 m时准确度还有待进一步的研究。

［1］苑静，宋文华，张茹，等.原油储罐池火灾状态下消防救援安全距离的研究［J］.消防科学与技术，2009，28(2):124-126.

［2］李慧.工业罐区池火灾灾害过程的数值模拟研究［D］.南京:南京工业大学，2005.

［3］史光梅，李明海，胡绍全等.池火灾数值模拟研究进展［J］.消防技术与产品信息，2010(9):39-43.

［4］CRAIG L B.Fire Hazard Calculations for Large，Open Hydrocarbon［M］.SFPE Handbook of Fire Protection Engineering，2nded，National Fire Protection Assiciation，2002.

［5］THOMAS P H.The Size of Flames from Natural Fires［C］.Ninth Symposium(International)on Combustion.Pittsburgh，Combustion Institute，1962:844-859.

［6］HESKESTAD G.Engineering Relations for Fire Plumes［J］.Fire Safety，1984(7):25-32.