自适应窗口滑动的物联网数据流典型相关分析

马帅营，陈志奎，刘 旸，张清辰，阿古达木

(1.大连民族学院网络与信息技术中心辽宁大连116605;2.大连理工大学软件学院辽宁大连116620)

物联网数据通常表现为大量的、时变的、无法预测的数据流，其挖掘研究为学术界广泛关注。其中，数据流典型相关分析(Canonical Correlation Analysis，CCA)属于数据流挖掘的难点问题之一，对其研究能够检测数据流之间是否相关、相关模式是否发生变化，为关联规则挖掘以及数据挖掘的后期处理提供参考。

数据流的典型相关分析属于数据流挖掘的难点问题之一，相关文献较少［1-4］。文献［1］对多维数据流采用近似算法实现典型相关分析。文献［2］采用不等概列采样技术约减流元组的数量，形成概要矩阵，然后在概要矩阵的基础上增量地计算多维数据流之间的前k个典型相关系数。文献［3］为了提高相关性分析算法的计算效率，提出为样本方差阵与协差阵组成的乘积阵降维的高效低价近似方法。但是，这些算法主要关注如何提高相关性分析的计算效率，并未考虑实际情况中，数据流速率变化这一复杂因素对相关性分析的实时性、准确性和有效性的影响。其中，文献［3］假定“无线传感器网络具有统一的采样时钟”，即各WSN数据流的速率是一致且保持不变。但是，事实上物联网中各个WSN很难保证统一的采样频率，并且WSN数据采集包含多种模式:基于周期的数据采集;基于事件触发的数据采集;基于查询的数据采集WSN的这些特点决定了物联网数据流具有变化和不一致的速率。因此，传统的基于滑动窗口的相关性分析算法不适用于实际的物联网数据流相关性分析。

针对以上问题，提出一种基于自适应窗口滑动的物联网数据流典型相关分析算法，根据数据流速率的变化，对滑动窗口进行自适应设计、动态调整窗口的滑动策略，最后将其应用在物联网数据流之间的相关性分析之中。

1 相关理论

1.1 典型相关分析

相关关系是事物之间的一类常见关系。现实应用中，数据流常常显露出较强的相关性，典型相关分析是研究两组变量之间相关关系的一种多元统计方法，能够揭示出两组变量之间的内在联系，最早由Hotelling于1936年提出［5］，不仅可直接用于相关性检测，而且可用于特征融合［6］和数据降维［7-8］等领域。

1.2 物联网数据流的典型相关分析

以物联网感知层中无线传感器网络为例，如图1。区域X和Y中分别部署了p个和q个传感器，分别感知区域中的不同事件源信息，这些传感器所采集的数据以流的形式达到物联网数据处理中心，表示为p维和q维数据流。物联网数据流的典型相关分析主要实现随着时间l的增加，实时计算物联网数据流X(l)和Y(l)之间的典型相关系数及典型相关变量，以此来判断区域X和Y中事件是否相关;如果相关，又是哪些传感器感知的信息占有主导作用;以及如何实现实时监测物联网数据流之间的相关性。

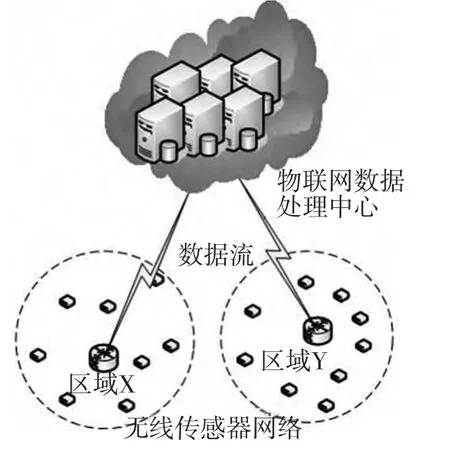
图1 物联网中无线传感器网络的数据流

2 基于自适应窗口滑动的物联网数据流CCA算法

2.1 CCA计算有效性和实时性问题

物联网数据流的典型相关分析，有两个关键问题。第一，数据流处理的实时性需要考虑数据流的速率。如果数据流速率较低，不应当一直等待数据到达，而应当设定最大等待时间，以满足CCA计算实时性要求。第二，CCA算法的执行时间与待处理数据的规模相关，也就是和滑动窗口内数据所构成的矩阵规模相关。在数据流维数一定的前提下，如果滑动窗口内包含的数据元组数过多，则CCA处理时间过长，无法满足数据流处理的实时性要求;相反，如果元组数过少，则统计样本少，会造成相关性不显著、计算精度低，因而不足以验证数据流的相关性。这就需要依据数据流的速率特性，设计适当的滑动窗口模型和窗口滑动方法，以保证物联网数据流典型相关分析的实时性、准确性和高效性。针对此问题，提出了基于自适应窗口滑动的物联网数据流典型相关分析算法。

2.2 符号及定义

定义1(数据流) 数据流可以被看作是一个允许元素重复出现的无限集合:

定义2(滑动窗口) 设数据流按照时间戳的先后顺序进入滑动窗口。任意时刻每个滑动窗口中的数据可以表示成序列:

滑动窗口分为两类［9］，一类是基于元组个数定义的滑动窗口，此时窗口内保存最近到来的K个元组，即在任意时刻序列W满足条件u-l=K;另一类是基于时间定义的滑动窗口，此时存储最近T时间内到达的元组，即在任意时刻序列W满足条件tu-tl=T。

本文使用基于时间定义的滑动窗口模型。

定义3(窗口宽度) ∀w∈W，滑动窗口w如定义1所示，tu-tl定义为 w的宽度，记作 Wid(w)。

定义4(窗口元组数) ∀w∈W，滑动窗口w如定义1所示，当Wid(w)=tu-ti时，u-l定义为w的窗口元组数，记为Size(w)。

定义5(数据流速率) ∀s∈S，t时刻数据流s的速率记为R(t)，代表单位时间内到达的数据元组个数。

由定义3和5可得，滑动窗口w的元组数Size(w)与数据流速率R(t)满足关系:Size(w)=R(t)dt。此公式是处理数据流速率变化、以及不同速率数据流的重要基础。

样本含量对典型相关系数的显著性有较大影响［10］，所以下面给出有效窗口宽度的定义。

定义6(有效窗口宽度) 有效窗口宽度定义了w中元组数Size(w)的最小值，记为EffWin。对于滑动窗口w，当满足:Size(w)=R(t)dt≥Eff-Win时，CCA的计算才有效。反之，当Size(w)=R(t)dt＜EffWin时，窗口w内包含的元组数过少，会造成相关性不显著、计算精度低，因而不足以验证数据流的相关性。依据物联网数据流的维度数、数据统计特性，选取适当的有效窗口宽度EffWin值，对于保证数据流典型相关分析的实时性、准确性和高效性有重要意义。

定义7(最大等待时间) 定义最大等待时间Δt，使得在 Δt时间内至少对数据流计算一次CCA，以满足物联网数据流典型相关分析的实时性要求。

定义8(有效窗口所需时间) 定义有效窗口所需时间为 TEffWin，满足R(t)dt=EffWin。TEffWin表示，若以有效窗口宽度EffWin为步长进行窗口的滑动，则下一滑动窗口w达到EffWin所需的时间。其中，TEffWin是和数据流速率R(t)相关的一个变值，在本文中满足TEffWin≤Δt。

定义9(CCA计算时间)。TCCA表示对数据规模为(EffWin×(p+q))的数据流计算一次CCA所需要的时间。在本文中满足TCCA≤TEffWin。

2.3 临界速率计算及自适应窗口滑动

数据流的处理以自适应的、近似查询为其核心技术［11］。因此首先计算数据流的两个临界速率，并以此为基础设计不同的窗口滑动策略，以保证数据流典型相关分析的实时性、准确性和高效性。

依据数据流处理实时性和有效性的要求，由定义6和7可知，当满足公式R(t)dt=Eff-Win时，可以得到临界速率R1。当数据流的速率R(t)≤R1时，R(t)dt≤EffWin，则每隔 Δt对数据流计算一次CCA，滑动窗口以Δt为步长进行滑动。同时，下一滑动窗口w的结束时间为tu+1=tu+Δt，w 的开始时间tl+1由公式 Size(w)=R(t)dt=R(t)dt=EffWin计算得到。此时，既满足了数据流处理的实时性，又保证了CCA计算的有效性。

由于数据流速率在短时间内变化较小，所以，对于以上两个临界速率可以采用估算的方式获得，即 R1=EffWin/Δt和 R2=EffWin/TCCA。

另一个问题是:物联网数据流之间可能存在速率差异，从而造成相同时间内滑动窗口中的数据元组数的差异。由于CCA计算需要两数据流的滑动窗口具有相同的元组数，所以对于数据流速率不一致的情况，首先需要保证两数据流滑动窗口都达到有效窗口宽度EffWin的要求:

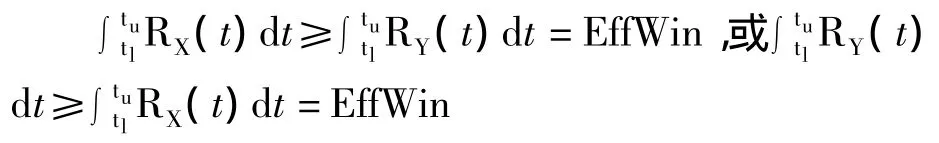
而对于超出EffWin的元组，则可以通过采样的方式将数据元组数降低到有效元组个数。

2.4 算法流程

依据所计算的临界速率及自适应窗口滑动策略，算法具体流程如下:

也许与王羲之喜鹅有关，华堂村的白鹅养殖历史悠久，远近闻名.华堂村的白鹅养殖一直是一家一户主要利用天然杂草、采用传统的放牧方式养殖，在本地集市上出售，收益很低.随着放牧地减少，现在几乎没有农户饲养了.

输入:tu时刻数据流X和Y，其维数分别为p和q，速率分别为RX(t)和RY(t);

步骤1 初始化参数最大等待时间Δt、有效窗口宽度EffWin和CCA计算时间TCCA;

步骤2 计算临界速率R1和R2;

步骤 3R(t)=MIN(RX(t)，RY(t));

步骤4 数据流速率与临街速率对比及策略选择:

如果R(t)≤R1，则以Δt为步长进行窗口滑动;

如果R1＜R(t)≤R2，则以 EffWin为步长进行窗口滑动;

如果R(t)＞R2，则以TCCA为步长进行窗口滑动;

步骤6 计算CCA;

输出:tu时刻数据流X和Y之间的典型相关系数 ρk和对应的投影向量 αk和 βk(k=1，2，…，p)。

3 实验

利用提出的算法模拟物联网数据流的实验，说明算法的执行流程及效果。

实验选取UCI标准数据集:臭氧含量检测数据集 (Ozone Level Detection Data Set，ODS)［12］。该数据集包括两组数据，分别记录了1小时和8小时的观测值，样本容量为2536，有效维数为71维。另外，对该数据集缺失值进行填充处理，为满足数据流模拟实验要求，采用对ODS数据集进行复制接续的方式解决。

ODS数据集为静态采样，本实验给定仿真速率函数R(t)=MIN(RX(t)，RY(t))模拟数据流速率的不同情况。

R(t)=5×(10+humps(0.01×(-0.7×t+160)))

并给定 Δt=10s，EffWin=500，TCCA=1s(Matlab中CCA计算矩阵规模为500×(71+71)的实际时间为0.935 502)，得到临界速率值为R1=50和R2=500。实验结果如图2。

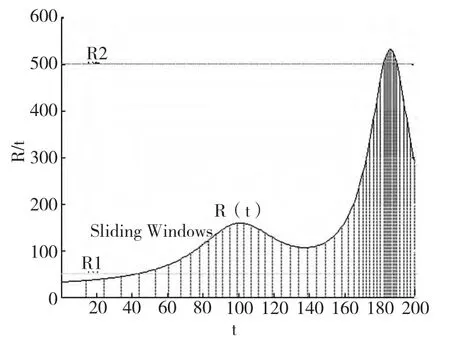
图2数据流速率和自适应窗口滑动

当数据流速率低于50时，则以最大等待时间Δt=10 s为步长进行窗口的滑动;当数据流速率在50和500之间时，则以EffWin=500为步长进行窗口滑动，相应的滑动时间随数据流速率而变化;当数据流速率高于500时，则以TCCA=1 s为步长进行窗口滑动，并对到达的数据进行采样将数据量缩减到EffWin=500。实验结果验证了自适应窗口滑动策略和动态调整滑动窗口宽度的思想，从而保证了数据流典型相关分析的实时性、准确性和高效性。

对以上的滑动窗口计算CCA所得部分结果如表1。

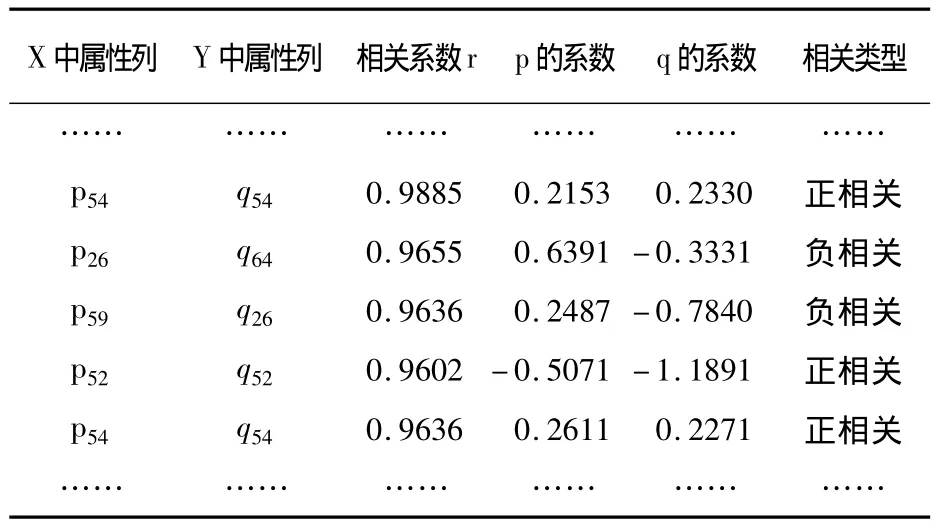
表1 数据流X和Y的典型相关分析部分结果

实验结果表明，针对物联网数据流的典型相关分析，可以用来判断事件源X和Y的相关性，同时可以定量判断具体是哪些传感器感知的信息占主导作用，以及相关模式的性质，进而为物联网数据流的关联规则挖掘以及数据挖掘的后期处理提供参考。

4 结论

传统的数据流典型相关分析分析算法没有考虑数据流速率的动态特性，不适用于物联网的实际情况。针对物联网数据流具有变化和不一致的速率问题，依据典型相关分析理论，研究物联网数据流之间的相关性，提出基于自适应窗口滑动的数据流典型相关分析算法。实验结果表明，算法可以保证物联网数据流典型相关分析的实时性、准确性和高效性。

［1］WANG Yongli，ZHANG Gongxuan，QIAN Jiangbo.ApproxCCA:an approximate correlation analysis algorithm for multidimensional data streams［J］.Knowledge-Based Systems，2011，24(7):952-962.

［2］杨学梅，董逸生，徐宏炳，等.高维数据流的在线相关分析［J］.计算机研究与发展，2006，43(10):1744-1750.

［3］王永利，徐宏炳，董逸生，等.基于低阶近似的多维数据流相关性分析［J］.电子学报，2006，34(2):293-300.

［4］STUDIPTO G，GUNOPULOS D，NICK K.Correlating synchronous and asynchronous data streams［C］.Acm SIGKDD，USA，2003:529-534.

［5］HAROLD H.Relations between two sets of variates［J］.Biometrika，1936，28(3/4):321-377.

［6］孙权森，曾生根，王平安，等.典型相关分析的理论及其在特征融合中的应用［J］.计算机学报，2005，28(9):1524-1533.

［7］KAMALIKA C，SHAM M K，KAREN L，et al.Multiview clustering via canonical correlation analysis［C］.ICML＇09 Proceedings of the 26th Annual International Conference on Machine Learning，New York，USA，2009:129-136.

［8］OLCAY K，ETHEM A，OLEG V F.Canonical correlation analysis using within-class coupling［J］.Pattern Recognition Letters，2011，32(2):134-144.

［9］黄树成，曲亚辉.数据流分类技术研究综述［J］.计算机应用研究，2009，(10):3604-3609.

［10］张路.典型相关分析应用常见问题分析及处理［J］.沈阳体育学院学报.2011，30(5)，125-127.

［11］杨颖，韩忠明，杨磊.数据流的核心技术与应用发展研究综述［J］.计算机应用研究，2005，(11):4-7.

［12］UCI氧含量检测数据集［EB/OL］.［2013-10-05］.http:∥archive.ics.uci.edu/ml/datasets/Ozone+Level+Detection.