考虑路面不平整度因素的车路耦合振动模型的建立

许海亮，袁 勇，屈铁军，唐浚然

（1．北方工业大学 建筑工程学院，北京 100144；2．同济大学 地下建筑与工程系，上海 200092）

车辆与道路的相互作用问题，包括车辆和道路两个系统的研究，是一个新的研究领域。车辆在路面不平整度的激励下产生振动，这种振动反过来又作用于道路结构，引起道路结构的变形，进而又加剧了车辆的振动，因此必须把车路作为一个大的系统进行研究。路面不平整度作为一个随机的激励，使整个系统的研究要置于随机振动的理论范畴内来进行。

目前，不管是车辆方面还是道路结构方面的随机振动研究，都将车辆和道路系统分离进行。对于道路方面的研究主要采用两种方式：①利用车辆模型，研究路面随机不平整度激励下车辆的振动，并计算出车辆对路面结构的动力荷载，再以该荷载来研究路面结构的响应［1－3］；②直接假定某种波动荷载为模拟的车辆荷载进行道路结构的动力响应研究［4－5］。上述方法都没有完全反映出车路耦合振动的实际状况，有鉴于此，有必要对车路相互作用系统的振动响应作深入的研究。

1 传统车路道路模型

以往的研究认为，道路在车辆荷载作用下的变形较小，相对于路面不平整度引起的车辆振动来说可以忽略，因此对于车辆动荷载的研究均以车辆模型为基础。研究中应用较广的模型是四分之一车辆模型［3，6－7］，如图 1所示。

传统模型研究的主要思路：利用四分之一车辆模型，研究车辆在路面不平整度下的随机振动可以得到车辆对路面的动荷载，进而作为道路振动响应研究的输入。

传统模型将车辆和道路分开考虑，在随机振动分析中将路面假设为刚性，即道路系统不参与振动，这与实际情况是不符的。对于随机振动问题，是否考虑车路的耦合效应，势必会影响各振动自由度的频率分布，频率分布的改变对振幅的影响是不容忽视的，因此有必要就车路耦合效应对系统振动的影响作深入的对比分析研究。

图1 四分之一车辆模型Fig．1 Quarter vehicle model

2 车路耦合线弹性模型的建立及求解

2.1 车路耦合线弹性模型

鉴于传统研究模型当中的不足，本文在传统振动模型的基础上引入了道路结构体系，建立了新的车路耦合振动线性模型。在模型中道路结构中的路面和路基被分别看成一个整体参与振动，采用质量－弹簧－阻尼元件进行模拟。为了考虑道路结构中相邻质量块间的影响，在模型中引入了剪切弹簧和剪切阻尼元件，模型如图2所示。

图2 车路耦合线性模型Fig．2 The linear model of vehicle-pavement coupling system

图2中：M1为悬挂系统（车架、载重）的质量；M2为非悬挂系统（轮胎、轮轴）的质量；M3为路面系统的质量；M4为路基系统的质量；K1为悬挂系统刚度；K2为非悬挂系统刚度；K3为路面系统刚度；K4为路基系统刚度；KV3为路面系统中剪切刚度；KV4为路基系统中剪切刚度；C1为悬挂系统阻尼；C2为非悬挂系统阻尼；C3为路面系统阻尼；C4为路基系统阻尼；CV3为路面系统剪切阻尼；CV4为路基系统剪切阻尼；Z1为悬挂系统与非悬挂系统的相对位移；Z2为非悬挂系统与路面的相对位移；Z3为路面系统与路基系统的相对位移；Z4为路基系统与基准面的相对位移；δ（t）为路面不平整度。

2.2 车路耦合模型随机振动求解

由D’A lembert原理，车路耦合线性模型的振动方程为：

整个系统的振动微分方程可以用矩阵形式表达为：

根据随机振动相关理论，激励与响应间存在如下关系：

式中，δj（ω）、Zi（ω）分别为激励和响应的频率函数；Hij（ω）为频率响应函数，对于单一激励输入可简记为Hi（ω）。

对（5）式进行Fourier变换，并利用（6）式可以得到Hi（ω）（i＝1，2，3，4）。

依据随机振动理论，激励的功率谱密度函数Sδ（ω），和响应函数的功率谱密度 SZ（ω）间有如下关系：

同时可以得到：

式中 Si′（ω）和 Si″（ω）分别为响应函数的速度谱密度函数和加速度谱密度函数。

以上求解得到了振动系统在相对坐标下的响应函数，对于绝对坐标下的响应可依据随机振动相关理论利用相对坐标下的响应函数推导得出。

以车辆悬挂系统质量单元为例，设其绝对位移函数为 y1（t），根据定义有：

依据相关函数与功率谱密度的相关定理有：

式中：SZ1表示 SZ1（ω），在不引起混淆的情况下简记为SZ1。

以上推导了车辆悬挂系统质量单元的绝对位移函数为y1（t）和功率谱密度函数Sy1（ω）的表达式，同理也可以求得系统中其它质量单元的绝对位移函数和功率谱密度函数。

2．3 路面不平整度模型

目前有多种典型路面的谱密度表达式，本文采用如下形式［8－9］：

式中，Ω0为参考空间频率，Ω0＝0．1c／m。Gq（Ω0）为参考空间频率下的路面功率谱密度值，称为路面不平度系数。W为频率指数，在双对数坐标上功率谱曲线为一条斜线，一般取W＝2。

设汽车的行驶速度为v，路面不平度的空间频率Ω，圆频率ω，自然频率f间存在如下关系：

综合式（12）、（13）、（14）可得：

3 车路耦合模型的试验验证

文献［10］对车辆与路面间的相互作用进行了现场试验研究，通过在试验车辆的前后轴头处设置加速度传感器来测量轮轴处的加速度值，试验装置布置如图3所示。表1和图4分别给出了试验的试验参数和测量结果。

表1 现场试验参数［10］Tab．1 The parameters in field test

图3 车辆轴头处传感器布置［10］Fig．3 The sensor disposition at car axle

从图4中可以看出，车辆轴头处（即车辆非悬挂系统）加速度频谱中共有两个显著的峰值，第一个峰值出现在2．3 Hz附近，幅值为0．317，第二个峰值出现在17．5 Hz附近，幅值为0．385。

利用本文所提出的车路耦合随机振动模型对试验进行了模拟，考虑试验地点为高速公路，模拟计算采用了A级路面的路面谱；其它参数取值为：M1＝12．98×103kg，M2＝5．0×102kg，M3＝3．5×102kg，M4＝1．5×103kg，K1＝5．0×105N／m，K2＝1．5×106N／m，K3＝1．0×109N／m，K4＝2．5×107N／m，KV3＝1．0×108N／m，KV4＝4．0×105N／m，C1＝1．5×104N·s／m，C2＝5．0×103N·s／m，C3＝3．0×104N·s／m，C4＝5．0×103N·s／m，CV3＝2．0×104N·s／m，CV4＝3．0×103N·s／m，v＝70 km／s（道路部分的取值参考道路相关参数，并考虑了对实际应力扩散的修正）。

计算车辆非悬挂系统的加速度频谱如图5所示。

图4 后轮轴加速度功率谱［10］Fig．4 Acceleration power spectral density of rear axle

图5 耦合模型模拟结果Fig．5 Simulation result using the coupling model

图6 车辆悬挂系统垂向加速度功率谱对比图Fig．6 Vertical acceleration power spectral density comparison diagram of vehicle suspension system

由车路耦合模型模拟结果可以看出，车辆非悬挂系统也出现了两个明显的峰值，第一个峰值出现在2 Hz附近，幅值为0．26，第二个峰值出现在20 Hz附近，幅值为0．98。对比图4和图5可以发现，耦合模型计算结果能够反映出车辆的主要振动情况，与实测资料能够较好的吻合，幅值上的差别主要是由模型简化、车辆参数、路面不平整度的输入均会与实际情况出现偏差，同时测量过程也会出现误差所造成。但是从总体的趋势上说，车路耦合模型计算结果和实测资料吻合的相当好。

利用本文提出的耦合模型对试验中的其它成果进行模拟也得到了很好的吻合，这有力的证明了本文所提出的耦合模型的正确性。

4 车路耦合模型与传统模型的对比分析

车路耦合模型将车辆和道路作为一个大的系统进行随机振动研究，能够较好的反映出车辆和路面真实的振动情况。鉴于目前传统模型在研究中应用较为广泛，本文将车路耦合模型和传统模型进行对比分析以界定出各自的适用范围。

考虑到加速度是目前评价车辆自由度振动的主要指标，本文研究了模型中各自由度的加速度功率谱密度函数，同时为便于分析，各函数图形均表达为自然频率f的形式。计算过程中取C级路面的功率谱，耦合模型和传统模型所取相应参数均相同。选择计算参数如下：M1＝4．5×103kg，M2＝5．0×102kg，M3＝3．5×102kg，M4＝1．5×103kg，K1＝5．0×105N／m，K2＝1．5×106N／m，K3＝1．0×109N／m，K4＝2．5×107N／m，KV3＝1．0×108N／m，KV4＝4．0×105N／m，C1＝1．5×104N·s／m，C2＝5．0×103N·s／m，C3＝3．0×104N·s／m，C4＝5．0×103N·s／m，CV3＝2．0×104N·s／m，CV4＝3．0×103N·s／m，v为 30 m／s。

图6～图8分别为耦合模型和传统模型中车辆悬挂系统、车辆非悬挂系统的加速度功率谱对比图以及车辆道路间作用力的功率谱密度对比图。

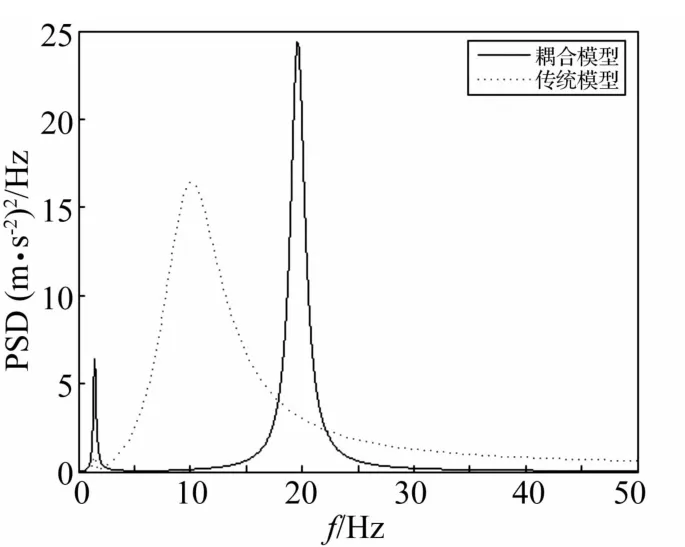
图7 车辆非悬挂系统垂向加速度功率谱对比图Fig．7 Vertical acceleration power spectral density comparison diagram of vehicle non-suspension system

图8 车辆道路间作用力功率谱对比图Fig．8 Power spectral density comparison diagram of the forces between vehicle and pavement

从图6～图8中可以分析得到以下几点结论：

（1）图6为车辆悬挂系统垂向加速度功率谱对比图，从图中可以看出耦合模型和传统模型中的曲线几乎完全重合，振幅峰值均出现在1．5Hz左右，这就意味着车路耦合效应对于车体悬挂系统（车体的主要部位）的振动影响不大。道路路面在车辆荷载下的变形通常是毫米量级，路面变形的影响对车辆主体的振动影响可忽略不计，所以车辆部门针对车辆振动的研究未考虑道路振动影响的方法是可行的。

（2）图7为车辆非悬挂系统垂向加速度功率谱对比图，可以看出耦合模型和传统模型中非悬挂系统的振动变化很大。耦合模型中非悬挂系统主要能量分布在1．5 Hz和20 Hz两处；而传统模型中只有一个峰值出现在10 Hz附近。通过与实测资料对比，利用传统模型计算得到的总体趋势与实测资料相差很大，而耦合模型所得总体趋势与实测资料吻合得较好。分析其具体原因，可以看出车辆非悬挂系统振动不仅受车辆悬挂系统的影响，而且受道路结构振动的影响也比较明显。

（3）图8对比了耦合模型和传统模型中车辆道路间作用力的功率谱图，从图中可以看出两个模型计算得出的作用力峰值均出现在1．5 Hz左右，与车辆悬挂系统的振动频率相近，符合车辆道路间作用力主要受车体悬挂系统影响的规律，这也间接证实了耦合模型计算的正确性。但是两者的振动幅值相差甚大，耦合模型中车辆道路间作用力的振幅峰值是传统模型的8倍多。若按照随机作用力的最大值为3σ（σ为均方差）来评估，耦合模型中车辆道路间作用力的最大值是传统模型的2．4倍（注：这里的作用力是中心化的，不包括车辆的静载作用力，以下同）。由此可见，车辆道路间的作用力受车路耦合效应影响较大，以往研究中考虑到道路的变形相对于路面不平整度来说量值较小而忽略车辆耦合效应的方法对于车辆道路间作用力带来的误差不容忽视。追究两模型所得数值相差较大的原因，发现考虑道路的耦合效应后，车辆非悬挂系统的振动频率发生了变化，其中一处振动峰值频率与悬挂系统频率相近，在该频率处车辆的悬挂系统和非悬挂系统发生了共振，从而使车辆道路间作用力的幅值成倍增大。

5 结 论

（1）建立了车路耦合线弹性模型，经实测数据验证该模型能够很好的反应车路耦合系统的振动情况。虽然数学上建立更为复杂的车路耦合模型不存在任何困难，但是本文建立的模型形式简单，计算方便，能够很好的反映实际振动情况，有很高的研究应用价值。

（2）利用车路耦合模型和传统模型进行对比分析，发现车路耦合效应对于车辆悬挂系统的振动影响较小；对于车辆的非悬挂系统及车路间作用力影响较大，因此考察非悬挂系统的振动以及路面结构所受的随机动荷载不能忽视车路耦合的影响。

（3）利用车路耦合模型研究了车路耦合效应对车路间随机动荷载的影响，发现耦合效应对车路间动荷载的影响不容忽视，实际算例显示耦合效应下车路间最大作用力（中心化）是不考虑耦合效应的2．4倍。

（4）分析车路耦合效应对车辆道路间随机动荷载影响较大的原因，发现考虑车路耦合效应后，车辆非悬挂系统的振动频率分布发生了变化，使其在车辆悬挂系统主振频率处出现共振，从而使车路间随机动荷载幅值比不考虑耦合幅值成倍增加。

（5）该模型虽考虑了车路耦合效应的影响，但并没有反映出车辆跳动与路面分离这一工况，还需要在今后的研究工作中进一步完善。

［1］Cebon D．The dynamic unteraction between wheeled vehicles and road surface［D］．Cambridge University Engineering Department，Ph．D．Dissertation，June，1985．

［2］Mikhail M Y．Three dimensional mechanistic analysis of vehicle-pavement interaction［D］．Arizona State University，Ph．D．Dissertation，December，1996．

［3］孙璐，邓学均．速度与车辆动态特性对于车路相互作用的影响［J］．土木工程学报，1997，30：34－40．SUN Lu，DENG Xue-jun． The influences of speed and dynamic gharacteristics of truck on vehigle-pavement interactions［J］．China Civil Engineering Journal，1997，30：34－40．

［4］张艳美．高速公路路基的动力特性研究［D］．兰州：兰州铁道学院，2001．

［5］陈华．交通荷载作用下公路路基的动力有限元分析［D］．兰州：兰州理工大学，2004．

［6］邓学均，孙璐．车辆－地面结构系统动力学［M］．北京：人民交通出版社，1998．

［7］王直民，张土乔，吴小刚．不平整路面上的车辆等效动载系数［J］．浙江大学学报，2007，41（6）：1007－1011．WANG Zhi-min， ZHANG Tu-qiao， WU Xiao-gang．Equivalent vehicle dynamic load coefficient on rough pavement［J］．Journal of Zhejiang University，2007，41（6）：1007－1011．

［8］赵济海，王哲人，关朝雳．路面不平度的测量分析与应用［M］．北京：北京理工大学出版社，2000．

［9］中华人民共和国国家标准．车辆振动输入路面平度表示方法（GB7031－86）［S］．国家标准局批准，1986．

［10］陈静．车辆与路面相互作用的基础研究：［D］．吉林：吉林大学，2002．

［11］陈果．车辆－轨道耦合系统随机振动分析：［D］．成都：西南交通大学，2000．

［12］徐昭鑫．随机振动［M］．北京：高等教育出版社，1990．

［13］胡津亚，曾三元．现代随机振动［M］．北京：中国铁道出版社，1989．

［14］叶尔骅，张德平．概率论与随机过程［M］．北京：科学出版社，2005．

［15］Wu S Q，Law S S．Dynamic analysis of bridge with non-Gaussian uncertainties under a moving vehicle［J］．Probabilistic Engineering Mechanics，2011，26（2）：281－293．

［16］Zhang Y W，Lin J H，Zhao Y，et al．Symplectic random vibration analysis of a vehicle moving on an infinitely long periodic track［J］．Journal of Sound and Vibration，2010，329（21）：4440－4454．

［17］王亚，陈思忠，郑凯锋．时空相关路面不平度时域模型仿真研究［J］．振动与冲击，2013，32（5）：70－74．WANG Ya，CHEN Si-zhong，ZHENG Kai-feng．Simulation research on time domain model of road roughness with timespace correlation［J］．Journal of Vibration and Shock，2013，32（5）：70－74．