危岩破坏激振信号频域特征研究
陈洪凯,唐红梅,王 智,何晓英
(1.重庆交通大学 岩土工程研究所,重庆 400074;2.三峡大学 水利与环境工程学院,宜昌 443002)
危岩崩塌是我国山区主要地质灾害类型,具有泛生性、突发性、强致灾等特征,严重威胁着山区公路、铁路交通运输、城镇居民以及矿山开采安全,国土资源部2012年发布的全国地质灾害通报表明,近10年来我国平均每年产生崩塌灾害2000次以上,如2010年发生5575起、2011年发生2319起,占发生地质灾害总数的30%~40%,直接经济损失超过13亿元/年。砂岩、灰岩地区的危岩体通常具有群聚性,崩塌灾害连锁特征明显,如武隆鸡尾山特大型崩塌灾害,存在突出溃裂窗[1]。唐红梅等[2]通过室内模型试验发现,危岩块突发性崩落对相邻危岩块的稳定性态要造成不利影响,称之为激振效应;陈洪凯等[3]采用突变理论分析了危岩破坏瞬间可能出现的弹冲加速度和弹冲速度。可以推断,激振效应是危岩聚集体连锁崩塌致灾的重要影响机制。在岩石动力特性相关研究中,刘军忠等[4]对角闪岩在冲击压缩荷载下的动态力学性能进行了试验研究;何思明等[5]揭示了地震波荷载作用下岩体裂纹扩展并最终诱发失稳破坏的力学机制;Sambuelli[6]对爆破振动条件下岩体介质质点的峰值振动速度进行了理论推导;Liang等[7]对爆破作用下岩体介质的振动速度的不同计算方法进行了对比研究。本文依托危岩破坏激振效应测试数据,判别激振信号质量的优劣,通过对激振信号进行小波分解,探讨危岩破坏激振信号的频域特征,研究成果对于科学揭示群发性危岩破坏机制具有积极意义。
1 危岩破坏激振效应模型试验
针对坠落式危岩,建造试验模型如图1所示,布置了三个加速度传感器测点(图2),其中1#测点位于第一层危岩体的第12#危岩块中部,2#测点位于第一层危岩体的第13#危岩块中部,3#测点位于第二层危岩体的第22#危岩块中部。模型中,第11#危岩块为起崩块,该模型试验重点关注起崩块崩落瞬间在相邻的第12#、13#和22#危岩块表面测点所采集的激振信号,为激振加速度,所采集试验数据有13万余个。,如1#测点激振加速度时程曲线(图3),危岩破坏瞬间激振作用历时约30 s,并且无论是x方向还是y方向的激振信号均呈现典型的衰减特性,y方向的激振信号强度明显大于x方向的激振信号强度。

图1 危岩破坏激振效应试验模型Fig.1 Experimental model of excitation effect for perilous rock to rupture
2 试验结果分析
图3所示的危岩破坏激振信号时程曲线是探讨危岩破坏激振信号频域特征的基础资料,信号时程曲线反映的是信号的时域特征,经过Fourier变换获得信号的频域特征[8],而信号的频域特性则是探讨信号能量分布的关键环节。
2.1 激振信号质量判别
危岩破坏激振信号质量的优劣直接关系到分析结果的科学性。目前,相干系数分析是判别信号质量的有效方法之一[9]。相干函数又称凝聚函数,表示信号输出与输入之间在频域上的相关程度,定义为:


图2 试验模型上传感器布置方案Fig.2 Arrangement ofsensors on test model

图3 1#测点激振信号加速度-时程曲线Fig.3 Acceleration-schedule curve for signals of1#measuring point
式中,Gxy(f)为输入输出信号的互频谱平均值;Gxx(f)为输入信号的自频谱的平均值;Gyy(f)为输出信号的自频谱的平均值。
相干系数在0到1之间变化,即当测试信号不受噪声污染时,相干系数为1,当测试信号完全被噪声淹没时,相干系数趋近于0,因此,相干系数可表征量测信号被噪声污染的程度,换言之,相干系数可用于判别信号测试质量的好坏。
基于危岩破坏模型试验结果,以1#、2#、3#测点 x方向的激振信号为例,进行激振信号相干系数分析,分析结果如图4所示。由于1#测点紧邻崩塌源,2#测点和3#测点相对于1#测点而言,属于输入信号,1#测点属于输出信号。图4清楚地表明,本次模型试验过程中所量测的危岩破坏激振信号之间的自相干系数接近于1,线性关系良好,表明所采集的危岩破坏激振信号受测试仪器、环境因素等造成的噪声污染微弱,激振信号质量较高,可用于进行激振信号频域特征分析。
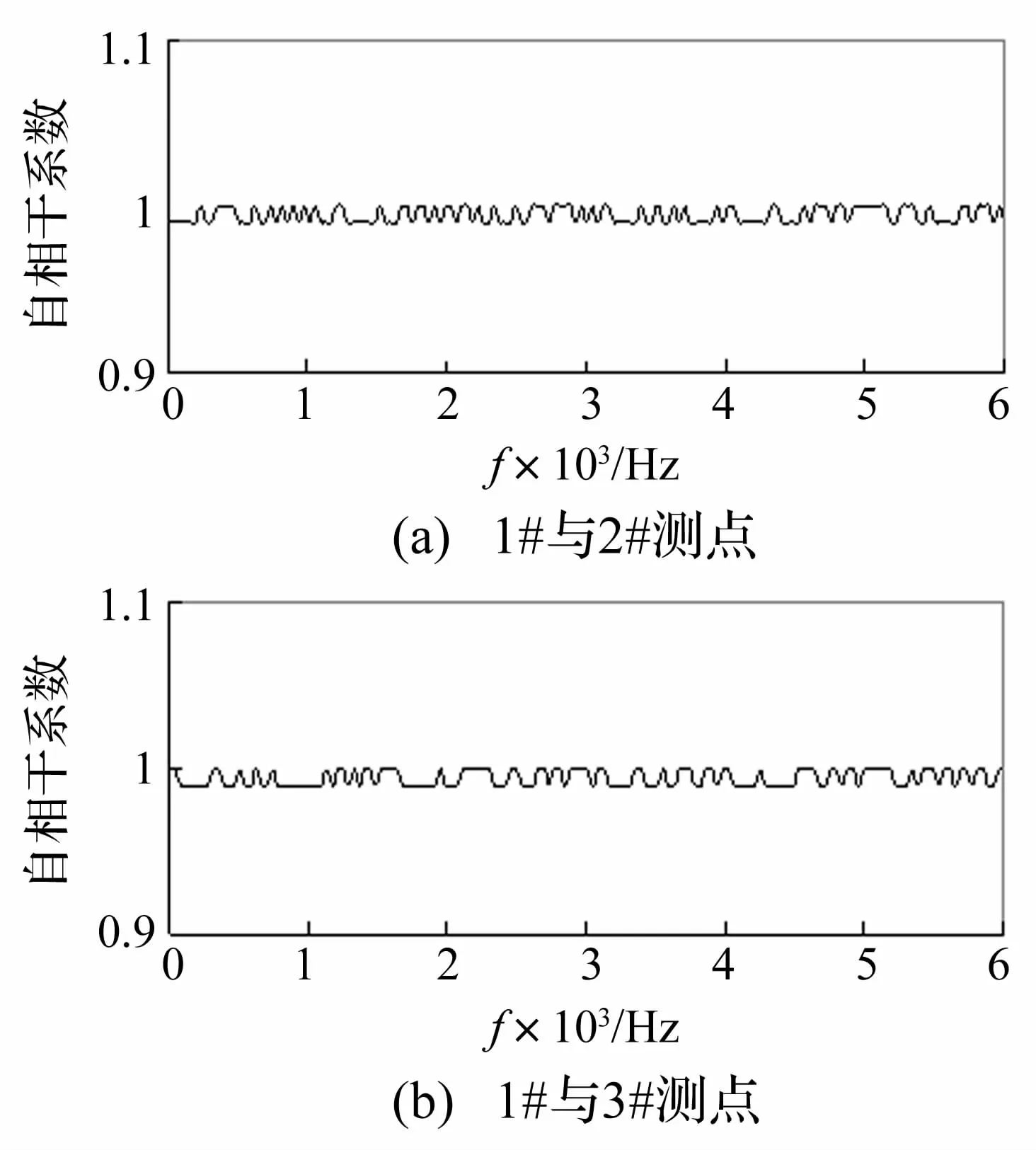
图4 x方向激振信号相干函数图Fig.4 Coherent function chart of x direction signal
2.2 激振信号小波分解
采用db8(3层)小波处理方法,对模型试验中1#、2#和3#测点水平方向(x方向)和竖直方向(y方向)的激振信号即激振加速度进行离散分解。db8(3层)小波处理重构所得近似系数对应于a3、d3、d2和d1共4个频率带,其中a3频率带范围为0~1 250 Hz,d3频率带范围为1 250~2 500 Hz,d2频率带范围为2 500~5 000 Hz,d1频率带范围为5 000~10 000 Hz,由于危岩破坏激振试验所采集信号均位于0~1 250 Hz内,故激振信号仅对a3频率段进行小波处理,激振信号小波分解近似系数时程变化如图5所示。
从图5可看出实验条件下危岩破坏激振信号小波分解近似系数具有如下特征:

图5 激振信号小波分解近似系数时程变化Fig.5 Acceleration-schedule curve of excitation signal under approximate coefficient wavelet decompose
(1)激振信号小波分解所得的水平方向的近似系数,1#测点最大,为 22 m/s2,3#测点最小,仅 11.3 m/s2,竖直方向的近似系数也具有类似特性,1#测点最大,约为30 m/s2,2#测点和 3#测点分别为 29.6 m/s2和 14 m/s2,这表明测点与激振源之间的距离和危岩块之间结构面的完整性对激振信号小波分解近似系数有较大影响:1#测点所处的第12#危岩块右侧临近激振源,激振信号小波分解近似系数最大;由于1#测点所处的第12#危岩块与2#测点所处的第13#危岩块之间的主控结构面上部分为不连续面,下段连续,而第12#危岩块与3#测点所处的第22#危岩块之间的界面均为不连续面,危岩块之间界面完整性越好,激振信号小波分解近似系数较高,信号能量损失越小。
(2)对同一测点,激振信号小波分解所得的近似系数,竖直方向的数值大于水平方向的数值,如1#测点水平方向的数值为22 m/s2,而竖直方向的数值可及30 m/s2,这表明坠落式危岩块破坏瞬间所产生的激振效应竖直方向体现得更明显些,这一特征对于科学评估危岩崩塌灾情、进行治理工程设计有积极意义。
(3)对于激振信号小波分解近似系数时程变化频率而言,3#测点水平方向激振信号小波近似系数变化频率较小,1#测点和2#测点近似系数频率变化规律正好相反,水平方向较大,竖直方向较小,这表明危岩块之间的完整性对于激振信号传递的影响是显著的,1#测点所处的第12#危岩块和3#测点所处的第22#危岩块之间的界面虽然接触良好,但属于完全不连续面,对于传递水平方向的激振信号敏感性较差。
2.3 激振信号的频谱变化特性
将危岩破坏激振信号小波分解近似系数时域谱进行Fourier变换转变为频域,获得各测点小波分解近似系数频谱图(图6),可据此探讨激振信号的频域特性。

图6 激振信号小波分解近似系数频谱图Fig.6 Distribution chart of frequency spectrum for signal under approximate coefficient wavelet decomposel
从图6可看出实验条件下危岩破坏激振信号小波分解近似系数频谱具有如下特征:
(1)激振信号频谱总体呈现衰减趋势,但衰减过程中分别在900 Hz、1 100 Hz和1 500 Hz频率处出现三个峰值,其中3#测点水平方向1 500 Hz峰值基本消失、竖直方向仅出现在900 Hz处,表明危岩破坏产生的激振能量具有突发性特征,能量衰减过程具有非恒定周期振动特性。
(2)测点与激振源之间的距离对激振信号衰减过程中代表性频谱的强度大小有较显著影响,如在1 100 Hz频率处:水平方向1#测点激振加速度为1.67 m/s2,2#测点激振加速度为1.56 m/s2,是1#测点的 0.93倍,竖直方向1#测点激振加速度为2.91 m/s2,2#测点激振加速度为 2.36 m/s2,是1#测点的 0.81倍;在同一个测点,竖直方向信号强度大于水平方向的信号强度,如1#测点竖直方向强度是水平方向信号强度的1.75倍,2#测点竖直方向强度是水平方向信号强度的1.51倍。
(3)危岩块之间界面的完整性也显著影响着激振信号的强度大小及传递特性,如1#测点所处的第12#危岩块和3#测点所处的第22#危岩块之间的界面属于危岩块叠置较好的不连续面,激振信号穿过该界面后衰减显著,如水平方向1 100 Hz频率处激振加速度由1.67 m/s2衰减到0.31 m/s2,1 500 Hz频率处激振加速度由 0.75 m/s2衰减到 0.14 m/s2,竖直方向衰减更为明显,1 100 Hz和1 500 Hz频谱峰消失,仅在900 Hz处有所显示,强度由1.01 m/s2衰减到0.29 m/s2;而1#测点所处的第12#危岩块与2#测点所处的第13#危岩块之间的主控结构面上部分为不连续面,下段连续,激振信号传递效果优于完全不连续面,如水平方向1 100 Hz频率处激振加速度仅由1.67 m/s2衰减到1.56 m/s2,衰减率6.59%,竖直方向仅由2.91 m/s2衰减到2.36 m/s2,衰减率 18.90%。
值得指出的是,1#测点激振信号低频段强度消失,其原因需要进一步探索分析。
3 结 论
危岩突发性破坏产生的激振效应,可用激振加速度表征危岩破坏激振信号,是危岩聚集体连锁崩塌的重要影响因素之一。基于坠落式危岩室内模型试验,本文对激振信号的频域特征进行了分析,得到如下主要结论:
(1)可以采用相干系数分析法判别危岩破坏激振信号质量的有效性,模型试验量测的危岩破坏激振信号自相干系数接近于1.0。
(2)实验量测到的危岩破坏激振信号均处于a3(0~1 250 Hz)频率带内,采用 db8(3层)小波处理方法,对量测到的危岩破坏激振信号进行近似系数重构处理,获得不同测点激振信号小波分解系数时程变化曲线,据此通过Fourier变换,获得危岩破坏激振信号小波分解近似系数频谱图。
(3)危岩破坏激振信号总体呈现衰减趋势,但衰减过程中分别在900 Hz、1 100 Hz和1 500 Hz频率处出现三个峰值,表明危岩破坏产生的激振能量具有突发性和非恒定周期振动特性。
(4)测点与激振源之间的距离越小,激振加速度越大,且竖直方向的量值均大于水平方向的量值,如1 100 Hz频率处,水平方向激振信号2#测点是1#测点的0.93倍,1#测点竖直方向强度是水平方向信号强度的1.75倍。
(5)危岩块之间界面的完整性也显著影响着激振信号的强度大小及传递特性,完整性越好,越利于激振信号的传递,竖直方向衰减率高于水平方向衰减率,如1 100 Hz频率处,水平方向激振信号衰减率为6.59%,竖直方向衰减率达到18.90%。
进一步研究中,应遵循本文研究思路,开展滑塌式危岩和倾倒式危岩破坏激振效应实验研究,分析滑塌式危岩和倾倒式危岩破坏激振信号的频域特征,对于开展该两类危岩的相似模型试验提供科学依据。
[1]陈洪凯,唐红梅,王林峰,等.危岩崩塌演化理论及应用[M].北京:科学出版社,2009.
[2]唐红梅,王智,陈洪凯,等.坠落式危岩崩落的激振效应与求解[J].振动与冲击,2012,31(20):32-37.TANG Hong-mei,WANG Zhi, CHEN Hong-kai, et al.Contribution ratio of excitation action triggered by collopse of perilous rock to stability of perilous rock[J].Journal of Vibration and Shock,2012,31(20):32-37.
[3]陈洪凯,张瑞刚,唐红梅,等.压剪型危岩破坏弹冲动力参数研究[J].振动与冲击,2012,31(24):33-36.CHEN Hong-kai,ZHANG Rui-gang,TANG Hong-mei,et al.Elastic&impulsive dynamic parameters of a ruptured compression-shear perilous rock[J].Journal of Vibration and Shock,2012,31(24):33-36.
[4]刘军忠,许金余,吕晓聪,等.冲击压缩荷载下角闪岩的动态力学性能试验研究[J].岩石力学与工程学报,2009,28(10):2113-2120.LIU Jun-zhong, XU Jin-yu, LU Xiao-cong, et al.Experimental study on dynamic mechanical properties of amphibolites under impact compressive loading[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):2113-2120.
[5]何思明,吴永,李新坡.地震诱发岩体崩塌的力学机制[J].岩石力学与工程学报,2010,29(A01):3359-3363.HE Si-ming,WU Yong,LI Xin-po.Collapse mechanism of danger rock triggered by earthquake[J].Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10):2113-2120.
[6]Sambuelli L.Theoretical derivation of a peak particle velocitydistance law for the prediction of vibrations from blasting[J].Rock Mech Rock Eng,2009,42(3):547-556.
[7] Liang Qing-guo,An Ya-fang,Zhao Lei,et al.Comparative study on calculation methods of blasting vibration velocity[J].Rock Mech Rock Eng,2011,44(1):93-101.
[8]陈洪凯,鲜学福,唐红梅,等.泥石流冲击荷载的时频分析方法及应用[J].防灾减灾工程学报,2011,31(3):255-260.CHEN Hong-kai,XIAN Xue-fu,TANG Hong-mei,et al.Timefrequency analysis method of debris flow impact loads and its application[J].Journal of Disaster Prevent and Mitigation Eng,2011,31(3):255-260.
[9]Donoho D L,Johostone I M.Adapting to unknow smoothness by wavelet shrinkage[J].Journal of The American Statistical Association,1995,90(432):40-80.

