霍普金森压杆过载实验弥散分析

刘 卫，孙晓霞，2，沈瑞琪，叶迎华

（1.南京理工大学 化工学院，南京 210094；2.辽宁北方华丰特种化工有限公司，辽宁 抚顺 113003）

分离式霍普金森压杆（Split Hopkinson Pressure Bar，SHPB）技术广泛用于测试如陶瓷［1］、混凝土［2］、岩石［3］及肉质［4］等材料的动态力学性能，而自由式霍普金森压杆（Free Hopkinson Pressure Bar，FHPB）技术广泛用于加速度传感器标定［5］。由于该技术能方便、快速产生高值加速度，张学舜等［6－7］利用霍普金森压杆过载实验技术评价火工品的抗过载性能，即通过对粘贴在压杆中间的电阻应变计采集的应变脉冲信号进行直接微分获得火工品过载加速度，但由于质点横向惯性运动引起应力波弥散现象影响，一维应力若存在偏差，霍普金森压杆沿轴向不同位置处加速度状态（峰值、脉宽）必不一致，导致所求火工品过载状态存在偏差。

为研究压杆中弹性波的弥散效应，Bancroft等［8－9］获得PochhammerChree频率方程的数值解。结果表明，用压杆半径、弹性模量、泊松比及密度等参数重建弥散应力波成为可能。Gong等［10］对特定泊松比的相关数据插值，获得相速与波长关系，并用傅里叶变换方法分析压杆应力波传播过程。通过联立插值公式与弥散波傅里叶展开式，使用傅里叶变换方法分析压杆的弥散效应成为可能。本文采用快速傅里叶变换法分析霍普金森压杆高过载实验中由弥散效应所致火工品过载状态偏差问题，以期获得火工品试件准确过载状态。

1 傅里叶弥散分析方法

1.1 过载加速度求解

自由式霍普金森压杆过载试验技术原理见图1。采用波形整形器进行加速度脉宽拓展实验，当撞击杆以一定速度向右运动时，先撞到粘贴在入射杆打击端的波形整形片，因其产生塑性变形，会在输入杆中产生一定上升沿的入射应力波沿输入杆轴向传播，并通过压杆－试件界面处传递至火工品试件，对其进行高加速度加载。

图1 自由式霍普金森压杆技术原理图Fig.1 Schematic of free Hopkinson bar apparatus

基于霍普金森压杆长径比较大，可将应力波视为一维应力波。据一维应力波基本理论，输入杆端面质点速度为

式中：εi，εr为压杆入射应变及反射应变；c0＝槡 E／ρ0为入射杆一维应力波速。

由于试件长度远小于入射杆，忽略应力波在试件内损失，入射波全部反射，εr为εi的倒像，即

实际上试件与输入杆端面粘接，由式（1）、（2）可得输入杆端面即试件速度v与加速度a值为

式中：v，a为试件质点速度、加速度；εi，c0，E，ρ0为自由式霍普金森杆入射应变、波速、弹性模量及密度。应变以压为正。

1.2 过载加速度弥散修正

据 PochhammerChree频率方程［8－9］在几个泊松比下数值解，Gong等［10］对数据进行插值，获得给定泊松比的相速与波长关系为

据该代数方程，可确定相速cn。若无弥散效应，且所有谐波成份相速均为c0，则所有谐波传播x距离时间均为x／c0；但由于弥散效应影响，某谐波成份以cn速度传播x距离所需时间为x／cn，则与无弥散效应相比，该条件下相角的改变量dn为

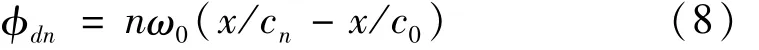
通过式（5）、（7）、（8）可获得弥散波中每一频率成份fn的相位。传播x距离时，弥散波的相角为

据修正后相角，即可重建有限长圆杆的应力波。传播x距离后，弥散修正后应变波的傅里叶展开式为

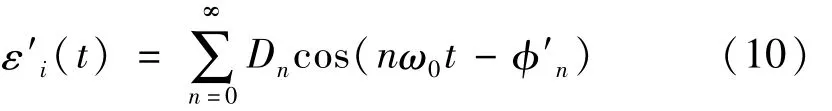
傅里叶变换中应变波εi转换到频率域的相角n可通过 cosn＝RE／（IM2＋RE2）1／2计算获得，RE与 IM分别为应变变换波的实、虚部；再利用新相角′n及幅值（IM2＋RE2）1／2经共轭处理即可得修正后入射应变变换波的实部RE′及虚部IM′，据此通过反向FFT变换即可获得传播x距离后时域上的应变波，即

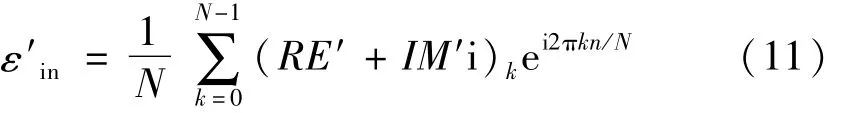
式中：N为数据点个数。

获得修正的应变波后即能据式（4）求出经弥散修正的加速度。

2 压杆过载状态分析

2.1 压杆过载加速度分析

圆弹性压杆由65Si2MnW材料制成，尺寸为Φ16×1 500 mm，一维弹性应力波速 c0＝5 163 m／s，泊松比ν＝0.30。为测量压杆沿轴向不同位置处加速度时间历程，在压杆相距377 mm位置各粘贴一对应变片，见图2，采集信号并计算两点处加速度时程。

图2 应变片粘贴位置Fig.2 Strain gages mounted on the pressure bar

在15.8 m／s撞击速度下，G1，G2处连续应变脉冲信号见图3。由图3看出，受弥散效应影响，应力波在压杆内传播中发生升时增加、震荡加剧现象，不利于用应变信号时间移位方法获得压杆或试件其它位置精确应变结果。

据式（4）计算G1，G2处加速度脉冲曲线，结果见图4。由图4看出，加速度峰值由G1处125 770 g减少至G2处99 150 g，脉冲宽度则由14μs增加至16μs。本文的加速度脉宽为全峰宽，但因加速度脉冲震荡较大，很难准确读出，据加速度脉冲与应变脉冲间存在的关联性，一般参考应变脉冲获取脉宽，将应变由0上升至最大值的时间差定义为加速度脉冲宽度。表明压杆沿轴向不同位置处质点加速度状态发生变化：随应力波在压杆内部的传播过载加速度峰值不断减小，而脉宽会略微增加。此因存在弥散效应，应力波沿压杆轴向传播时其升时不断增加，斜率减小，产生由应变微分过程所得加速度曲线峰值不断减小、脉宽增大现象。因此，在Hopkinson高过载试验中须对用应变计采集的加速度曲线进行弥散修正，以准确获取压杆任意位置的应变及加速度状态。

图 3 G1，G2处应变信号Fig.3 Strain pulse getting from G1and G2 gage

图4 G1，G2处加速度曲线Fig.4 Acceleration pulse getting from G1and G2 strain gage

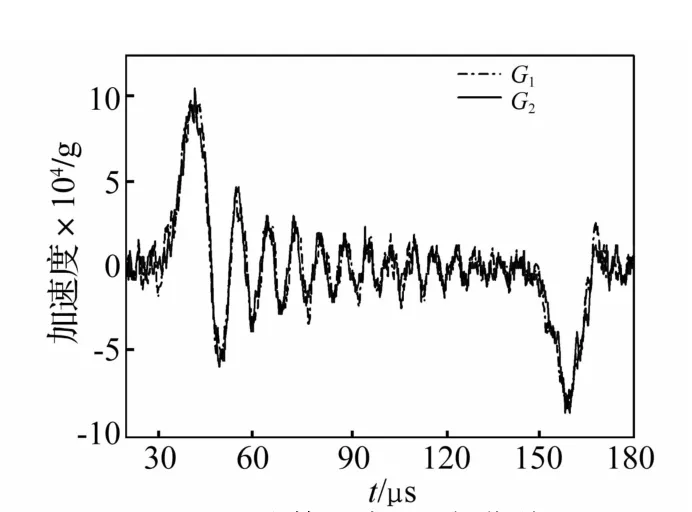
图5 G1处修正加速度曲线与G2处加速度曲线比较Fig.5 Comparison between corrected acceleration pulse at G1 gage and acceleration at G2 gage

2.2 波形传播过程弥散修正

为验证傅里叶弥散修正分析方法的正确性，本文以G2处加速度信号为基准，将G1处应变信号进行右行377 mm距离的弥散修正，再据式（4）将修正的应变信号转化成加速度信号，并与基准加速度曲线进行比较。若二者吻合则表明该方法准确、可靠。

由图5看出，G1处经右行修正的加速度曲线与G2处基准加速度曲线吻合较好，表明在采用G1处加速度状态评估G2处加速度状态过程中须对G1处加速度曲线进行弥散修正，才能获得符合实际的实验结果；若利用应变计处加速度状态表征压杆其它任意位置加速度状态，只要对用应变计所得应变信号进行一定距离的右行或左行弥散修正据式（4）求解加速度即可。

3 试件的过载加速度分析

脉冲整形技术已广泛用于材料的动态力学性能，以消除应变波形的高频震荡并实现试件应力均匀，获得恒应变率加载［11－12］。将脉冲整形技术引入霍普金森压杆过载实验，对保持较高加速度峰值及拓展加速度脉冲宽度，均取得良好效果。

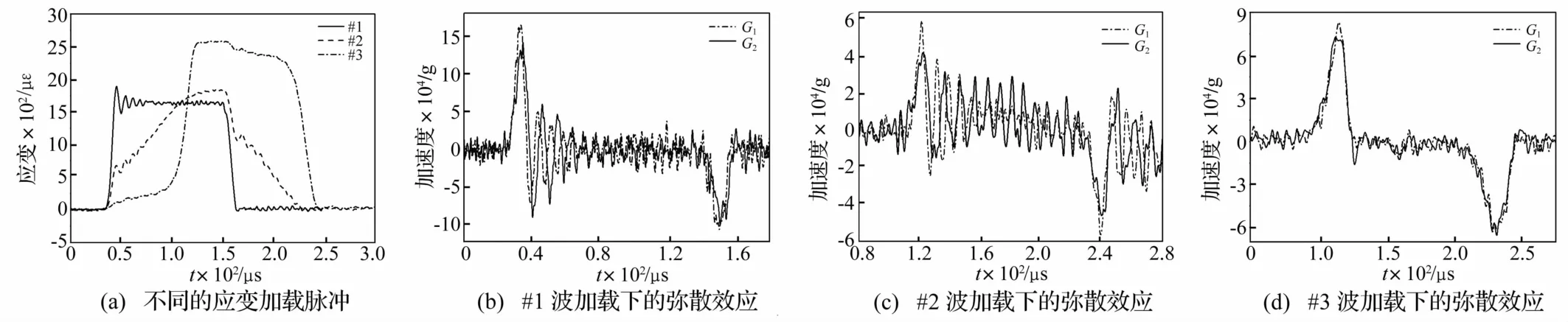
图6 不同脉冲加载的加速度弥散分析Fig.6 Dispersion analysis under the loading of pulses with different shape

不同条件下所得几种典型应变脉冲见图6（a）。其中＃1为15.8 m／s速度、未经整形时电阻应变计采集的应变曲线；＃2，＃3为依次用 Φ7.06×0.88 mm的 A3钢及 Φ3.04×2.00 mm的软铝整形器，分别在 18.7 m／s，25.1 m／s撞击速度下所得应变脉冲。由图6（a）看出，虽三种应变波形上升沿宽度不同，但在波形局部，三者均陡峭上升沿明显，此为对霍普金森压杆高过载实验的基本要求。过载加速度太小，较难满足火工品过载实验要求。试验中电阻应变片传感器粘贴于G1位置（图2）。试验后对＃1、＃2、＃3号应变曲线进行右行1.144 m弥散修正，获得置于入射杆端部试件所受过载加速度曲线见图 6（b）、（c）、（d）。由图 6（b）、（c）、（d）看出，在三种不同形状的连续脉冲加载条件下，经弥散修正后试件的过载加速度峰值均有降低，但加速度脉冲宽度略微增加。

对＃1、＃2、＃3脉冲加载所得及修正前后加速度峰值、脉宽分别进行偏差分析，结果见表1。由表1看出，无论采用何种脉冲加载，所得试件的过载加速度曲线峰值及脉冲宽度均有较大偏差，峰值偏差均在10%以上；脉冲宽度偏差因波形而异，脉宽越小的加速度修正后脉宽偏差越小，但绝对误差均小于6μs。即波形整形技术在提高加速度脉宽情况下若不能完全消除弥散效应对实验结果影响，须对应变计脉冲进行弥散修正，才能精确获得试件的过载加速度峰值及脉宽。此对实验方法的完善、建立准确数学模型至关重要。

通常不同作用脉冲，其上升沿越陡峭，高频成分越多、脉冲在圆杆中传播相同距离的弥散越大。由此表明，含陡峭上升沿的加载脉冲在传播过程中必存在弥散效应。而在霍普金森压杆高过载实验中，因含陡峭上升沿应变加载脉冲必然存在，否则所得加速度脉冲幅值必较小，无法满足高过载实验对加速度峰值104g的量级要求。因此对含陡峭上升沿的弥散应变脉冲，精确获得试件实际过载加速度，弥散修正必不可少。而不含高频成分的非弥散波，则无需弥散修正。

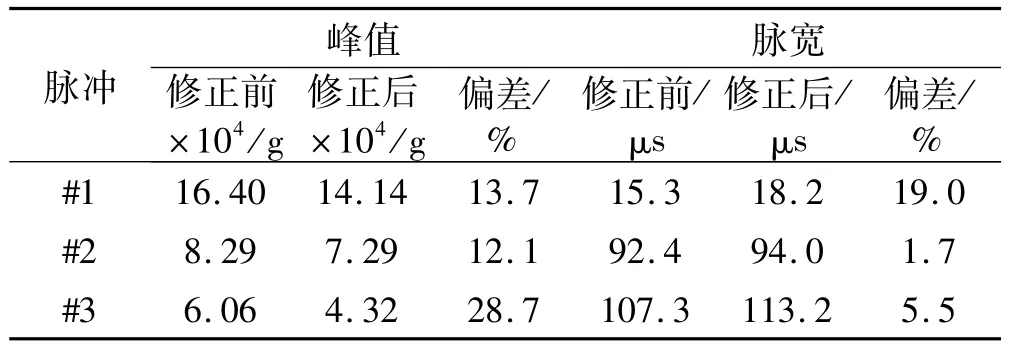
表1 弥散修正前后偏差分析Tab.1 Errors analysis before and after dispersion correction

4 结 论

（1）考虑压杆质点的横向运动，用傅里叶变换方法分析压杆应变及加速度脉冲传播过程的弥散效应；用双应变片法获得压杆不同位置的应变及加速度。通过比较证明由于弥散现象存在导致压杆不同位置加速度状态存在差异。

（2）用傅里叶变换弥散分析方法获得不同脉冲加载及弥散修正前后试件过载加速度间的偏差。结果表明，利用傅里叶变换进行弥散分析方法正确、可靠，且效果较好；为求得准确的过载加速度，对含高频成分的弥散波须进行弥散修正。

［1］Chen W N，Ravichandran G.Dynamic compressive failure of a glass ceramic under lateral confinement［J］.Journal of the Mechanics and Physics of Solids，1997，45（8）：1303－1328.

［2］Li Q M，Meng H.About the dynamic strength enhancement of concretelike materials in a split hopkinson pressure bar test［J］.International Journal of Solids and Structures，2003，40（2）：343－360.

［3］ Shan Renliang，Jiang Yusheng，Li Baoqiang.Obtaining dynamic complete stressstrain curves for rock using the split Hopkinson pressure bar technique［J］.International Journal of Rock Mechanics and Mining Sciences，2000，37（6）：983－992.

［4］王宝珍，胡时胜.猪后腿肌肉的冲击压缩特性实验［J］.爆炸与冲击，2010，30（1）：33－38.WANG Baozhen， HU Shisheng. Dynamic compression experiments of porcine ham muscle［J］.Explosion and Shock Waves，2010，30（1）：33－38.

［5］Forrestal M J，Togami T C，Baker W E，et al.Performance evaluation of accelerometers used for penetration experiments［J］.Experimental Mechanics，2003，43（1）：90－96.

［6］张学舜，沈瑞琪.火工品动态着靶模拟仿真技术研究［J］.火工品，2003（4）：1－4.ZHANG Xueshun，SHEN Ruiqi.Study on dynamic touchtarget analog simulation technique for initiating explosive devices［J］.Initiators and Pyrotechnics，2003（4）：1－4.

［7］杨光强，任炜，商弘藻.高过载下桥丝电雷管失效模式与机理初步研究［J］.火工品，2010（2）：8－11.YANGGuangqiang，REN Wei，SHANGHongzao.Study on failure mode and mechanism of bridgewire electric detonator under high overload［J］. Initiators and Pyrotechnics，2010（2）：8－11.

［8］Bancroft D.The velocity of longitudinal waves in cylindrical bars［J］.Physical Review，1941，59：588－593.

［9］Davies E D H，Hunter SC.The dynamic compression testing of solids by the method of the split Hopkinson pressure bar［J］.Journal of the Mechanics and Physics of Solids，1963，11（3）：155－179.

［10］Gong J C， Malvern L E， Jenkins D A. Dispersion investigation in the split Hopkinson pressure bar［J］.Journal of Engineering Materials and Technology，1990，112（3）：309－314.

［11］Kenneth SV，Fengchun J.Improved pulse shaping to achieve constant strain rate and stress equilibrium in splithopkinson pressure bar testing［J］. Metallurgical and Materials Transactions A，2007，38A：2655－2665.

［12］李志武，许金余，白二雷，等.高温后混凝土的SHPB试验研究［J］.振动与冲击，2012，31（8）：143－147.LI Zhiwu，XU Jinyu，BAI Erlei，et al.SHPB test for posthightemperature concrete［J］.Journal of Vibration and Shock，2012，31（8）：143－147.