基于时频分析的质量慢变转子系统非线性动力学特性研究
于 涛,王 娇,李英杰,孙 伟,韩清凯
(1.烟台大学 机电汽车工程学院,山东 烟台 264005;2.山东省高校先进制造与控制技术重点实验室,山东 烟台 264005;3.大连理工大学 机械学院,辽宁 大连 116024)
在分离、纺织、起重、电动、发电等机械中转子系统作为主要部件因工作环境及工况要求导致转子质量不断发生变化。如燃气轮机转子叶片受工作介质冲刷腐蚀、粘连堆积导致叶片质量发生改变;纺织机械的转子部件质量由缠绕物的多少随时间缓慢变化。传统上将此类转子系统称质量慢变转子系统[1-5]。而有关此类转子系统研究较少。Cveticanin[6-7]研究质量慢变转子系统非线性特性,包括自激振动及混沌运动等;王宗勇等[8-10]研究质量慢变转子系统松动、碰摩故障下周期运动及拟周期运动。
本文基于渐近解析法[11-12]获得简化集中质量模型质量慢变转子系统解析解,并采用重分布小波尺度图对具体质量慢变模型进行时频特征分析,获得丰富的质量慢变转子动力学行为。
1 质量慢变转子动力学方程
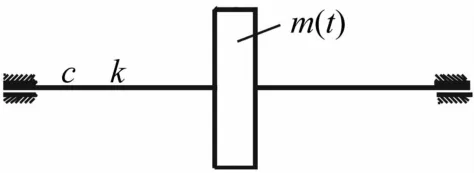
图1 基于简单集中质量的质量慢变Jeffcott转子Fig.1 Simplifiedconcentratedmass based model of Jeffcott rotor system with slowlyvarying mass
图1为Jeffecott转子系统,其质量随时间缓慢变化,该系统动力学方程为
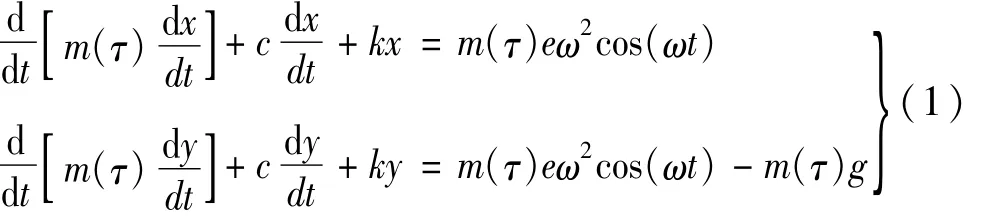
式中:m(τ)为转子慢变质量;c为转子系统阻尼系数;k为转轴线性刚度系数;g为重力加速度。
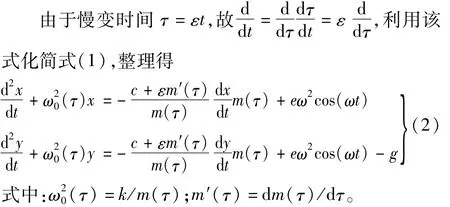
通过与恒定质量转子系统对比知,质量慢变转子系统增加一阻尼力项,且该项阻尼系数为慢变质量的函数。若质量由小到大变化则该慢变阻尼系数为正,反之为负,会产生自激振动;质量慢变转子系统固有频率亦为慢变的,亦会引起振幅、相位差角的慢变。阻尼力、激振力较小时令 c/m(τ)=2εξω0(τ),e=εr,则式(2)可化简为
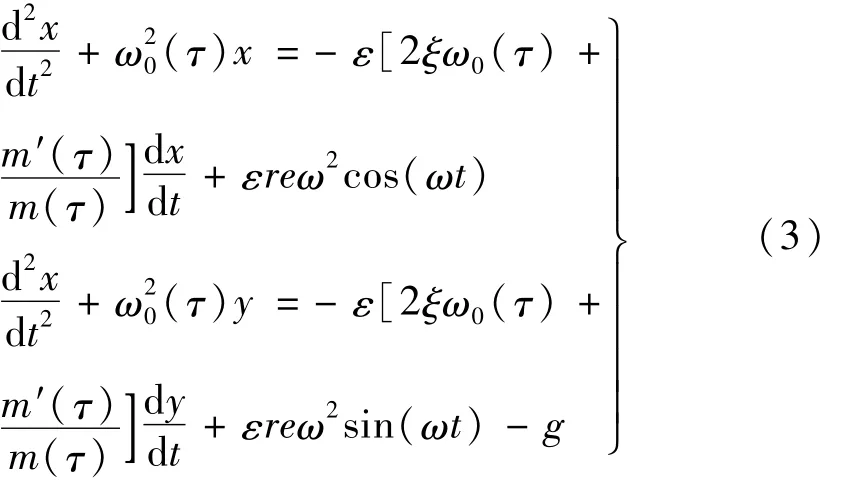
2 解析求解
由于式(3)的两方程互不关联可分别求解。以求解水平方向为例


式中:a,εu1(τ,a,t,ψ)为时间 t的函数。

取方程的一次近似解为
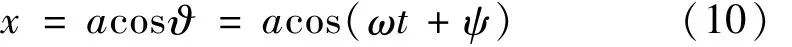
式中:a,ψ为时间t的函数,计算式为

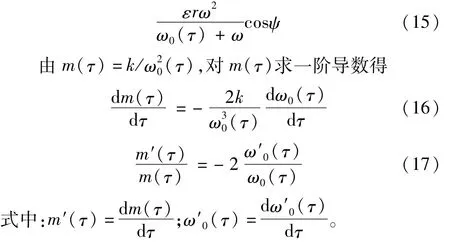
将式(16)代入式(14),整理得

3 基于解析解的质量慢变转子系统时频响应小波分析
对连续操作的分离机械而言,其转子质量可认为围绕某一质量上下波动,波动幅度取决于物料性质,波动频率取决于加料周期。为便于分析,令转子的慢变质量为

式中:k=48EI/L3,I=πd4/64为转轴截面通过形心的惯性矩,d=2R为转轴直径。
设Jeffcott转子模型半径R=10 mm,长度L=480 mm,弹性模量 E=2.06E11 N/m2,则转子轴刚度 K=43 888 N/m。令m0=1 kg,ξ=0.1,e=0.000 1 m,则27 Hz<f0<47 Hz。采用四阶Runge-Kutta法对微分方程组(20)数值求解。ωm=100 rad/s、ε=0.01、λ=0.5时取慢变质量转子系统稳态转速ω分别为20 Hz、30 Hz、40 Hz、60 Hz,所得质量慢变转子系统时频响应曲线见图2~图11。由图2看出,质量慢变转子系统低于系统固有频率稳态运转时,系统频率成分除工频外在27~47 Hz范围内出现密频成分。
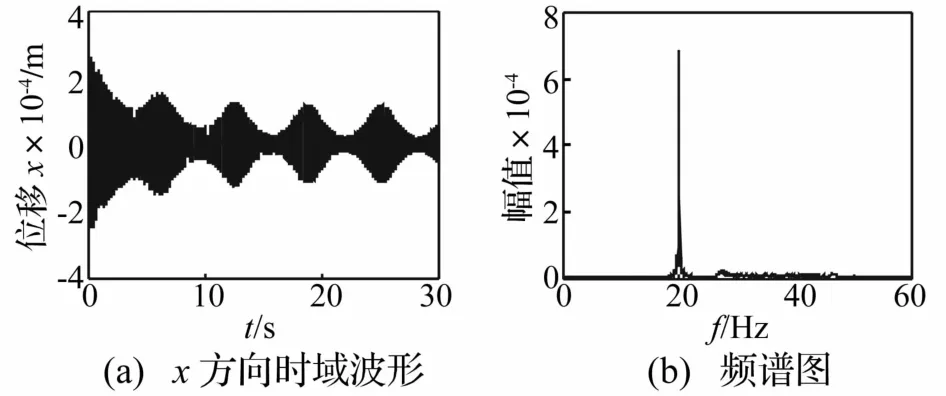
图2 质量慢变转子系统时频响应曲线(ω=20 Hz,ε=0.01)Fig.2 Timefrequency response of rotor system with slowlyvarying mass(ω=20 Hz,ε=0.01)
为更清楚观察该范围内的频率成分,对图2(a)时域波形进行高通滤波、频谱分析,所得时频曲线见图3。由图3看出,系统响应经高通滤波后低频成分消失,频谱图中显示出27~47 Hz间密频成分,但由于频率成分过于密集无法辨认,因此对滤波后的时域信号进行小波重排尺度分析,见图4。由图4看出,随时间推移,去除工频成分的质量慢变转子系统重排Morlet尺度图中转子频率按简谐特征波动,呈一条明显的简谐频率带,且以2π为周期,频率幅值波动渐小。
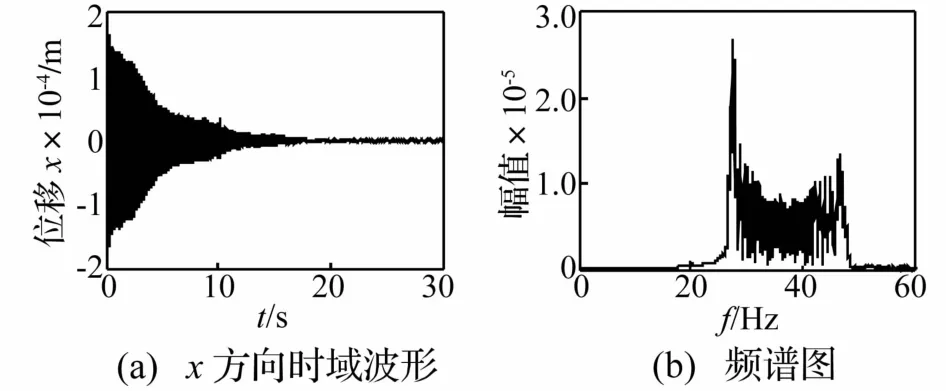
图3 高通滤波后转子系统时频响应曲线(ω=20 Hz,ε=0.01)Fig.3 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering(ω=20 Hz,ε=0.01)
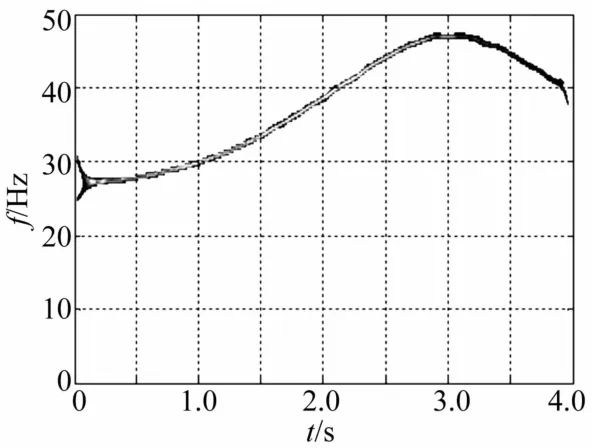
图4 高通滤波后质量慢变转子系统重排 Morlet尺度图(ω=20 Hz,ε=0.01)Fig.4 Reassigned morlet scalograms of rotor system with slowlyvarying mass after highpass filtering(ω=20 Hz,ε=0.01)
质量慢变转子系统以30 Hz、40 Hz在系统固有频率变化范围内稳态运转时,其时频响应曲线见图5、图7。由两图看出,系统存在丰富的频率成分,对时域信号进行FFT分析时在27~47 Hz之间存在密频成分,且转子工频湮没其中。系统响应重排Morlet尺度图见图6、图8。由两图看出,系统频率有2π的周期波动。
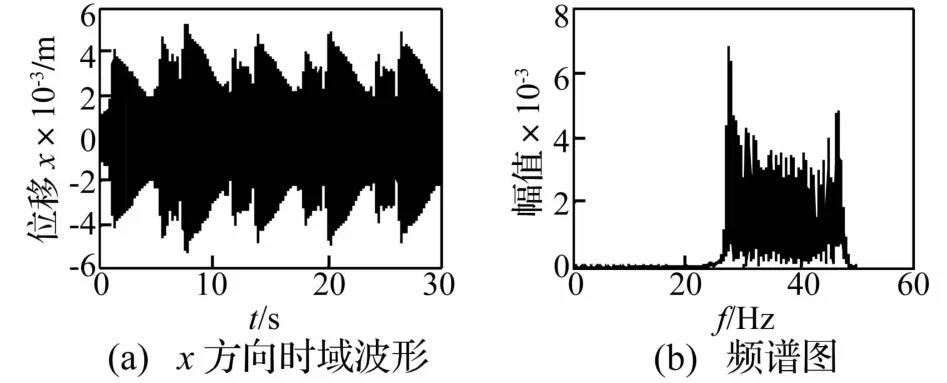
图5 质量慢变转子系统时频响应曲线(ω=30 Hz,ε=0.01)Fig.5 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering(ω=30 Hz,ε=0.01)
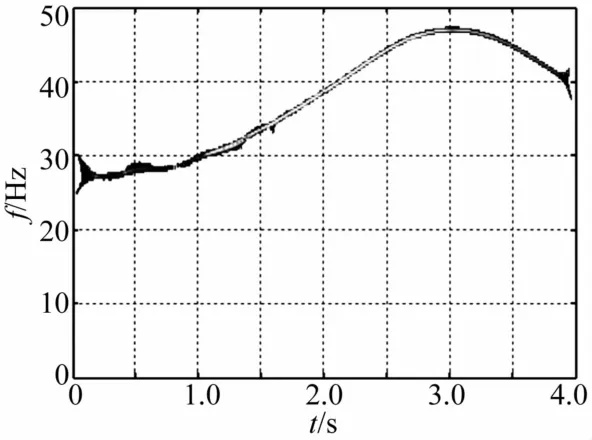
图6 质量慢变转子系统重排Morlet尺度图(ω=30 Hz,ε=0.01)Fig.6 Reassigned Morlet scalograms of rotor system with slowlyvarying mass(ω=30 Hz,ε=0.01)

图7 质量慢变转子系统时频响应曲线(ω=40 Hz,ε=0.01)Fig.7 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering(ω=40 Hz,ε=0.01)
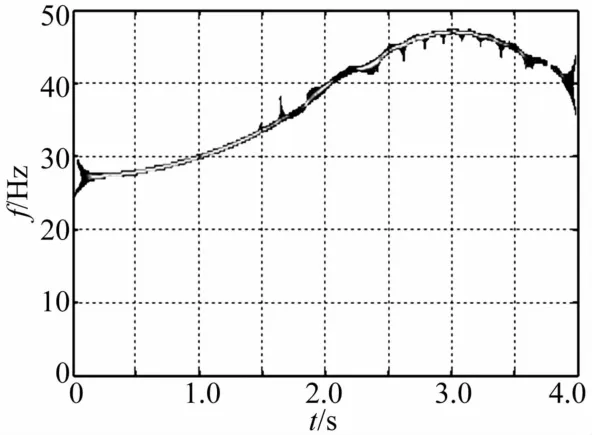
图8 质量慢变转子系统重排Morlet尺度图(ω=40 Hz,ε=0.01)Fig.8 Reassigned Morlet scalograms of rotor system with slowlyvarying mass(ω=40 Hz,ε=0.01)
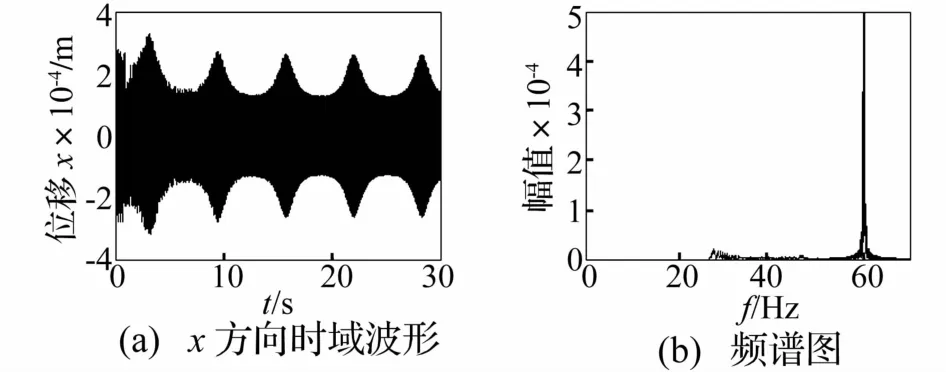
图9 质量慢变转子系统时频响应曲线(ω=60 Hz,ε=0.01)Fig.9 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering(ω=60 Hz,ε=0.01)
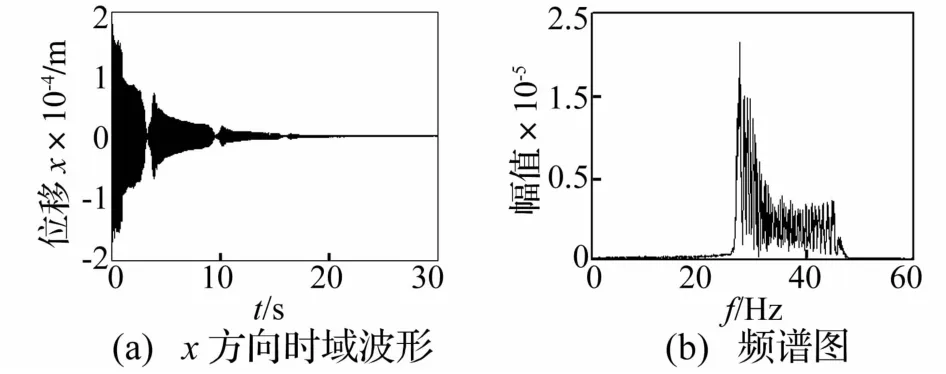
图10 低通滤波后的转子系统时频响应曲线(ω=60 Hz,ε=0.01)Fig.10 Timefrequency response of rotor system with slowlyvarying mass after lowpass filtering(ω=60 Hz,ε=0.01)
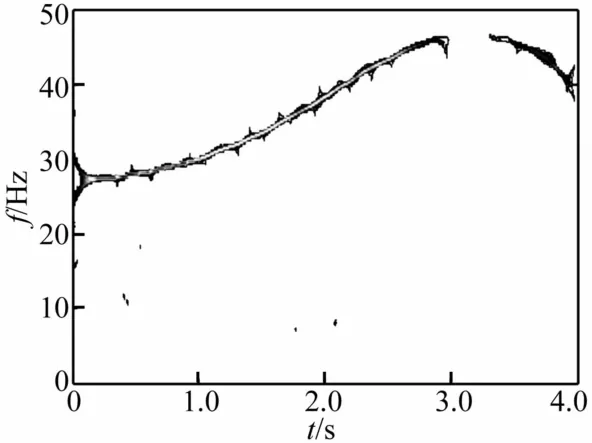
图11 低通滤波后质量慢变转子系统重排Morlet尺度图(ω=60 Hz,ε=0.01)Fig.11 Reassigned Morlet scalograms of rotor system with slowlyvarying mass after lowpass filtering(ω=60 Hz,ε=0.01)
质量慢变转子系统以60 Hz在超系统固有频率范围外稳态运转时,系统时域信号呈周期运动的时频响应见图9。由图9看出,除高频工频外在低于工频范围内亦存在密频成分。因此对时域信号进行低通滤波,滤波后慢变转子系统时频响应曲线见图10。由图10看出,低频部分从27~47 Hz为系统固有频率变化范围。系统响应重排Morlet尺度图见图11。由图11看出,系统低频部分作大周期的频率波动。
对给定参数的质量慢变转子系统时频响应特点,可认为在给定质量慢变模型下,系统频率响应存在T=2π/(ωmε)的大周期波动,频率波动周期 T=2π/(100×0.01)=2π。为考察质量慢变参数ε对系统响应影响,讨论 ωm=100 rad/s、ε=0.1、λ=0.5时质量慢变转子系统时频响应。取慢变质量转子系统稳态转速ω分别为20 Hz、30 Hz、60 Hz时,系统时频响应见图12~图19。转速为20 Hz时系统时频响应见图12。由图12看出,由于质量慢变导致系统固有频率时变,在工频附近出现多成分频谱,且频谱间相差 Δf=ωmε/(2π)=100×0.1/2/3.14=1.59 Hz;在高频区存在幅值相对较低的密频区。对时域信号进行高通滤波的时频图见图13。由图13看出,在20~50 Hz区间以20 Hz为基准,Δf为增量的连续频谱,系统以 T=2π/(ωmε)=1/Δf周期作频率波动。
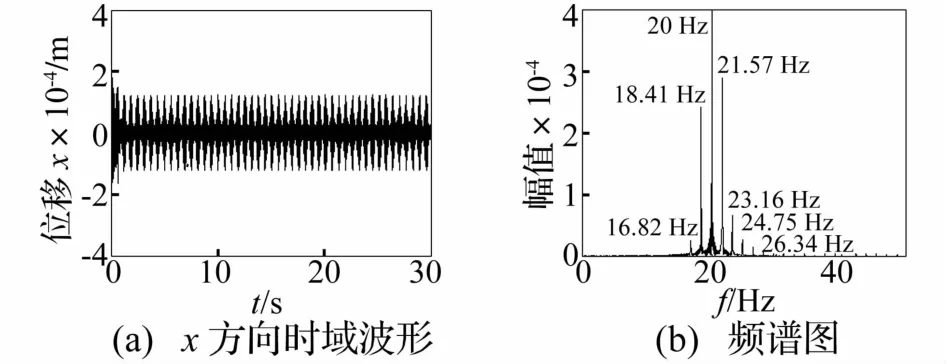
图12 质量慢变转子系统时频响应曲线(ω=20 Hz,ε=0.1)Fig.12 Timefrequency response of rotor system with slowlyvarying mass(ω=20 Hz,ε=0.1)
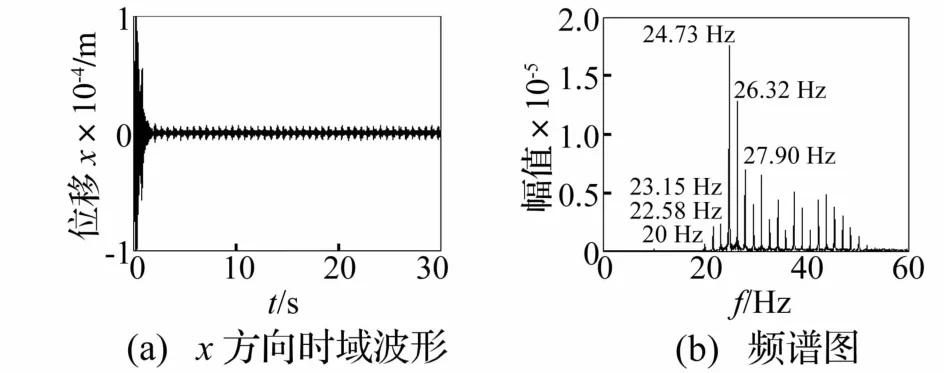
图13 高通滤波后质量慢变转子系统时频响应曲线(ω=20 Hz,ε=0.1)Fig.13 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering
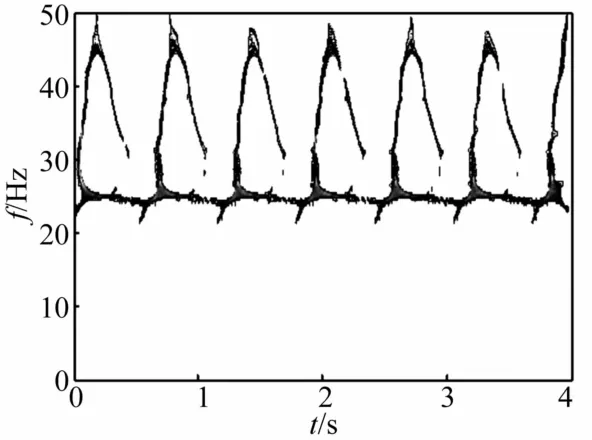
图14 高通滤波后质量慢变转子系统重排Morlet尺度图(ω=20 Hz,ε=0.1)Fig.14 Reassigned Morlet scalograms of rotor system with slowlyvarying mass after highpass filtering
质量慢变转子系统以稳态转速在30 Hz运转时,系统响应见图15、图16。由两图看出,系统稳定运转在固有频率变化范围内时,在共振区及附近以工频为基准Δf为增量,出现丰富的频率成分,且系统频率随时间的推移以 T=2π/(ωmε)=1/Δf周期作频率波动。
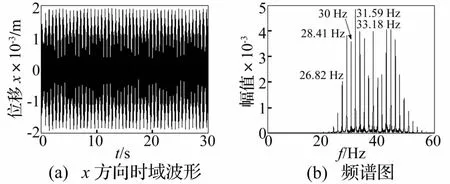
图15 质量慢变转子系统时频响应曲线(ω=30 Hz,ε=0.1)Fig.15 Timefrequency response of rotor system with slowlyvarying mass
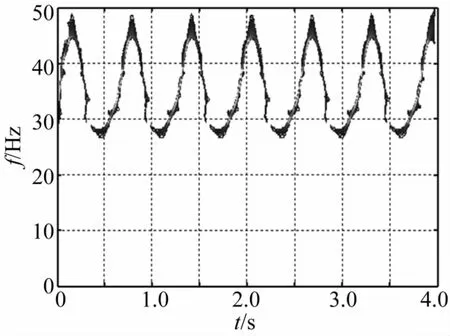
图16 质量慢变转子系统重排Morlet尺度图(ω=30 Hz,ε=0.1)Fig.16 Reassigned Morlet scalograms of rotor system with slowlyvarying mass
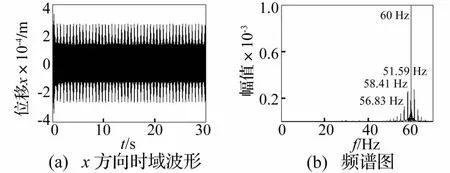
图17 质量慢变转子系统时频响应曲线(ω=60 Hz,ε=0.1)Fig.17 Timefrequency response of rotor system with slowlyvarying mass
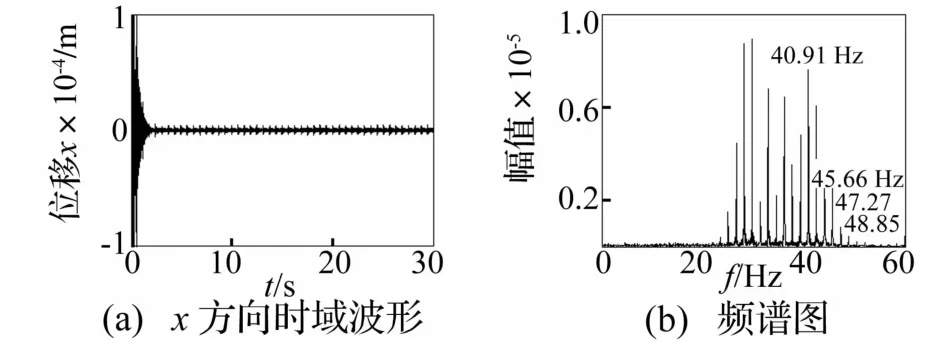
图18 低通滤波后质量慢变转子系统时频响应曲线(ω=60 Hz,ε=0.1)Fig.18 Timefrequency response of rotor system with slowlyvarying mass after lowpass filtering
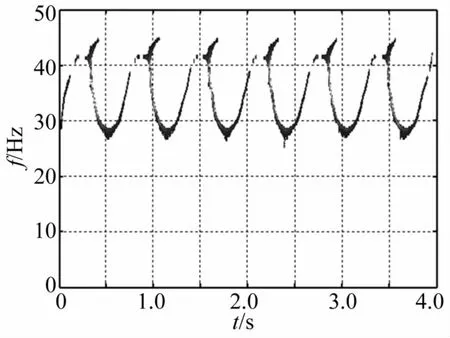
图19 低通滤波后质量慢变转子系统重排Morlet尺度图(ω=60 Hz,ε=0.1)Fig.19 Reassigned Morlet scalograms of rotor system with slowlyvarying mass after lowpass filtering
慢变质量转子系统以稳态转速在60 Hz运转时系统时频响应见图17。由图17看出,系统呈现与低于临界转速运转时的系统响应相似特点。因此对质量慢变模型 m(τ)=m0(1+λcos(ωmτ))而言,系统频率响应与ωm及 ε的乘积有关,即系统作周期为 T=2 π/(ωmε)的频率波动,频率成分随时间推移以工频转速为基准、Δf=ωmε/(2π)为增量进行简谐波动。
4 结 论
本文基于渐近法,给出质量慢变转子系统解析分析方法,推导出质量慢变转子系统响应的解析解,研究、讨论具有单一质量慢变模型的转子系统非线性动力学响应,结论如下:
(1)质量慢变导致系统固有频率产生时变,系统频率响应与ωm,ε的乘积有关,且频率成分随时间推移以工频转速为基准、以T=2π/(ωmε)为增量进行简谐波动。
(2)基于渐近方法的质量慢变转子系统响应解析解的一次近似解,对精度、分辨率而言已足够。
[1]闻邦椿,顾家柳,夏松波,等.高等转子动力学-理论、技术与应用[M].北京:机械工业出版社,2000.
[2]李以农,郑玲,闻邦椿.一类具有参数慢变的非线性振动系统[J].重庆大学学报,2000,23(6):16-18.LI Yinong,ZHENG Ling,WEN Bangchun.Study on the nonlinear vibration system with slowchanging parameters[J].Journal of Chongqing University,2000,23(6):16-18.
[3]米特洛波利斯基ЮА,著.吴沧浦,译.非线性振动系统中的不平稳过程[M].北京:科学出版社,1958.
[4]韩清凯,刘杰,闻邦椿.不对称滞回模型的一般形式及其参数慢变特性[J].振动与冲击,2000,19(3):14-16.HAN Qingkai, LIU Jie, WEN Bangchun. General formulations of asymmetrical hysteretic models and the slowlyvarying characteristics of their parameters[J].Journal of Vibration and Shock,2000,19(3):14-16.
[5]于涛.损伤转子动力学及其故障诊断若干关键问题研究[D].沈阳:东北大学,2007.
[6]Cveticanin L.Chaos in rotors with slowly varying mass[J].Journal of Sound and Vibration,1995,185(5):897-901.
[7]Cveticanin L.Normal mode of vibration for continuous rotors with slow time variable mass[J].Mech.Mach.Theory,1997,32(7):881-891.
[8]王宗勇,吴敬东,闻邦椿.质量慢变转子-滚动轴承系统的支承松动故障分析[J].中国机械工程 2005,16(13):1197-1200.WANG Zongyong,WU Jingdong,WEN Bangchun.Study on pedestal looseness faults of a rotorroll bearing system with slowly varying mass[J].China Mechanical Engineering,2005,16(13):1197-1200.
[9]王宗勇,龚斌,闻邦椿.激励幅值慢变转子系统的动力学研究[J].中国机械工程,2007,18(24):2969-2973.WANG Zongyong,GONG Bin,WEN Bangchun.Study on dynamics of rotor systems with slowly varying excitation magnitude[J].China Mechanical Engineering,2007,18(24):2969-2973.
[10]王宗勇.参数慢变转子系统动力学及其故障研究[D].沈阳:东北大学,2004.
[11]包戈留包夫НЯ,米特洛列斯基A,著.金福临,译.非线性振动理论的渐近方法[M].北京:科学出版社,1961.
[12]于海,陈予恕,曹庆杰.多自由度裂纹转子系统非线性动力学特性分析[J].振动与冲击,2014,33(7):92-98.YU Hai,CHEN Yushu,CAO Qingjie.Nonlinear dynamic behavior analysis for a cracked multiDOF rotor system[J].Journal of Vibration and Shock,2014,33(7):92-98.

