分布式摩擦激励下轴系振动研究

车凯凯，张振果，张志谊，华宏星

（1.上海交通大学 振动冲击噪声研究所，上海 200240；2.上海交通大学 机械系统与振动国家重点实验室，上海 200240）

舰船螺旋桨推进轴系支承较复杂，而艉轴承作为桨－轴－支承的重要组件直接关系系统的稳定性，多采用水润滑橡胶轴承［1］。低速重载下轴承与轴颈间不能形成良好润滑条件，使其工作在边界润滑或混合润滑状态，产生摩擦振动及噪声［2］进而影响舰船的隐身性能与生存能力［3］。

有关水润滑橡胶轴承摩擦振动研究多集中于摩擦性能、轴承润滑及摩擦噪声等［1］。文献［4－5］对水润滑橡胶轴承进行润滑机理及摩擦性能研究，文献［1，4，6－7］通过一般性试验研究，由粘－滑效应角度对摩擦噪声给予解释。Simpson等［8］用两自由度模型模拟轴承－轴颈摩擦诱导振动，利用摩擦力试验曲线［9］给出振动失稳的临界条件，并阐述粘－滑运动产生时的摩擦力变化规律。Mihajlovic等［10］探讨柔性转子摩擦诱导弯扭耦合振动，考虑不连续摩擦力模型与弯扭耦合诱发的扭转振动，认为摩擦－弯曲－扭转振动耦合作用客观存在。文献［11］分析摩擦激励及弯扭耦合作用对螺旋桨推进轴系振动影响规律，说明轴承－轴颈摩擦特性与小阻尼振动模态均为耦合系统出现摩擦自激振动的重要因素。对轴承支承的研究多采用将轴承支承简化为单点支承［11－12］。此等效处理方法适用短轴承，但当轴承较长时其合理性则需重新考虑；此外，点支承模型无法用于研究轴承分布支承及轴承倾斜等对轴系响应特性影响。

基于此，本文以低速重载轴系为研究对象，采用分布式轴承支承，建立轴系摩擦激励下系统振动非线性动力学模型，通过数值计算探讨摩擦激励响应与系统物理参数间关系，讨论转速、接触力、轴承倾斜等因素对轴系响应特征影响，为轴系耦合振动分析提供参考。

1 分布式摩擦模型

本文研究对象由转轴、水润滑橡胶轴承（BR2）、支座及两油润滑球轴承（BR1、BR3）组成，见图1。其中转轴分为具有不同截面特性的左、中、右三轴段。据研究假设为：① 左右两端油润滑轴承润滑良好，忽略其对系统振动影响；② 轴承在中间轴段长度方向的径向刚度均匀；③ 通过中间轴承座对BR2施加预载荷，以保证轴承－轴颈的持续接触状态，且轴承座可通过调节自身角度实现BR2倾斜。

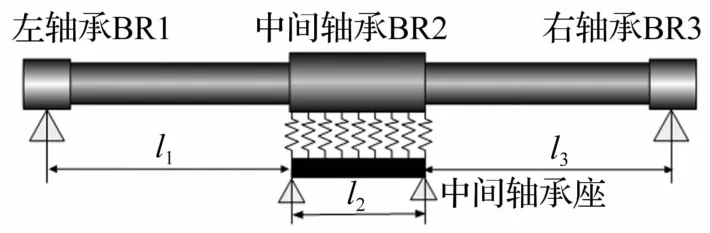
图1 分布式摩擦激励的分析模型Fig.1 Bearing friction test device

1.1 摩擦力数学模型

轴承－轴颈间接触特性可由分布式摩擦力F（x，t）描述，且假设其满足胡克定律，即摩擦力正比于分布接触正压力F（x，t）。为研究轴承摩擦对模型振动影响，须建立合理、有效的摩擦力数学模型。对液体润滑轴承，Stribeck曲线可清楚描述摩擦的各种润滑状态及转化过程，摩擦系数同载荷、速度及润滑液体粘度有密切关系［13］，在低速重载情况下，速度依赖型指数摩擦模型已得到广泛验证［14］。摩擦力计算公式为

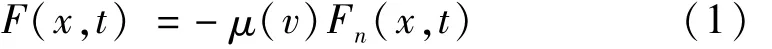
式中：v为轴承与轴颈间相对滑动速度；μ为动摩擦系数［14］，可表示为

式中：μ0，μ1，β0为由试验确定的参数；sgn（·）为符号函数。

1.2 耦合机理分析

据力系简化原理，分布摩擦力F（x，t）可等效为作用于转轴轴颈中心分布力 Ff（x，t）及分布力矩Mf（x，t），见图2。两者均能激发转轴相关振动。轴承－轴颈间相对滑动速度v、转轴转速n及摩擦力矩引起的扭转角位移Θ相关，可表示为

图2 轴承－轴颈接触受力示意图Fig.2 Contact force between the bearing and shaft

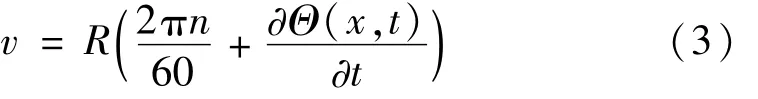
式中：Θ（x，t）／t为转轴扭转振动角速度。

由式（3）知v为变量，其变化可进一步改变摩擦力方向及大小，使转轴扭转振动与非线性摩擦相互耦合，导致自激振动。为确定分布摩擦力，需确定分布式接触正压力Fn（x，t）。由于摩擦激励与转子的陀螺效应会诱使转轴涡动，致接触载荷Fn（x，t）为变量，由轴系预载荷与由涡动派生的接触载荷组成。考虑的分布载荷见图3。

图3 分布载荷示意图Fig.3 Distributed load on the shaft

设转轴初始状态在预载荷作用下中间轴段所受分布载荷为n（x，α），且与同轴承座倾斜角度α有关；设分布载荷线性分布 n（x，α）＝k′x＋b，据N′推导出（num为所取分布弹簧个数）k′＝－kytanα／l2，b＝［2N′＋ky（x1＋x2）tanα］／（2l2）。

为保证轴承倾角α时轴承下部分与轴颈间发生紧密接触，需满足条件 n（x2，α）≥0。将 k′，b代入上式，推导出条件式 N′≥kyl2tanα／2。

在转轴横向振动作用下，中间轴段所受分布力为f（x，t），可表示为

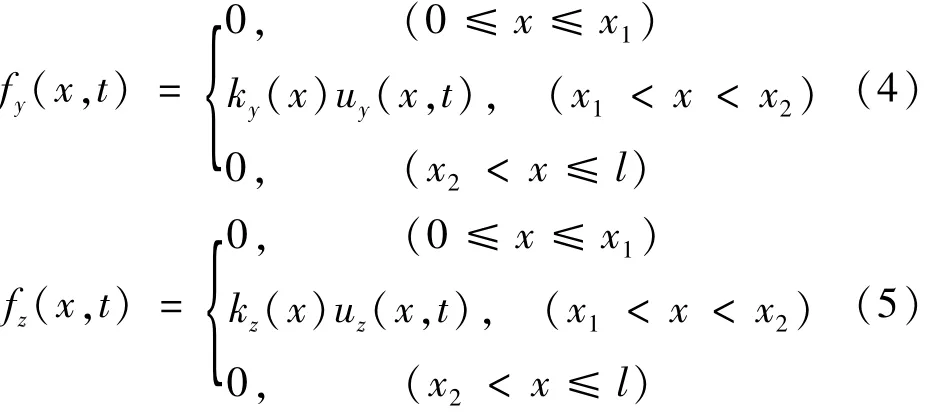
式中：ky（x），kz（x）为接触点处 y、z向轴承等效刚度；uy（x，t），uz（x，t）为接触点 y、z向位移；l2＝x2－x1。

由此可导出分布式接触正压力及摩擦力为

正压力：

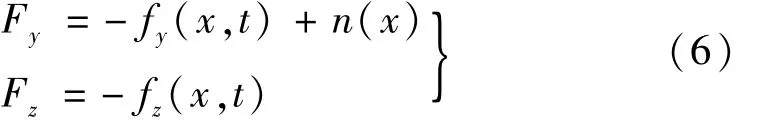
摩擦力：

由式（3）～式（7）知，轴系所受摩擦力及摩擦力矩为系统参数、摩擦参数的函数［11］，因此该系统具有力反馈与状态参数反馈，形成自振系统，摩擦激励及弯曲－扭转振动耦合作用为分析轴系自激振动基础。

2 非线性系统动力学模型

采用模态叠加法及拉格朗日方程建立该连续系统非线性动力学方程。利用通用有限元软件获取该变截面轴系主振型及模态频率，并通过三次样条插值方法将有限元软件所得振型列转化为振型函数列［12］。设轴挠度为 u（x，t），模态展开为

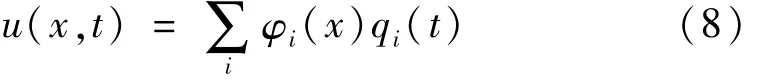
式中：φi（x）为第 i阶模态振型函数；qi（t）为广义坐标。设轴扭转位移为 Θ（x，t），模态展开为

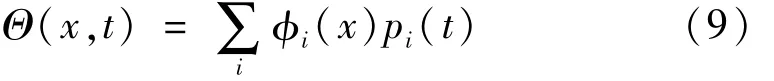
式中：i（x）为第 i阶模态振型函数；pi（t）为广义坐标。

利用主振型函数正交性，系统弯曲振动动能可表示为

系统弯曲振动耗散能可表示为

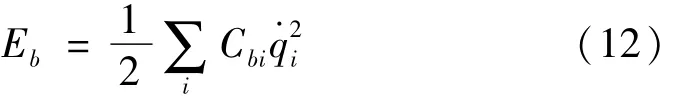
式中：Cbi为广义阻尼。由于系统模态阻尼通常难以确定，理论研究通常采用Rayleigh阻尼模型，即C＝α1M＋β1K，α1与 β1均为常数。

系统广义摩擦力可表示为

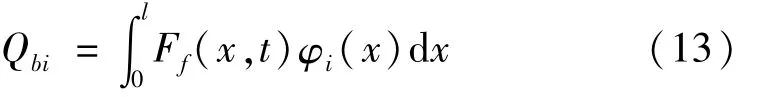
将式（10）～式（13）代入拉格朗日方程

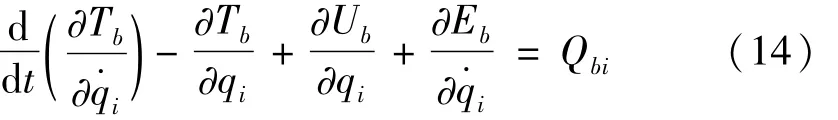
得弯曲振动下广义坐标动力学方程（下标表示y，z向）为

同样，系统扭转振动动能、势能、耗散能及广义摩擦力矩可分别表示为

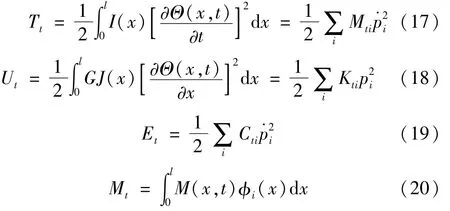
求解式（15）、（16）、（22）即可获得系统非线性动态响应。

3 求解结果与分析

3.1 求解参数

以某轴承试验系统为研究对象，讨论摩擦激励作用下耦合振动规律。图1为简化模型，计算参数为l1＝0.4 m，l2＝0.2 m，l3＝0.4 m，l＝1 m；三段轴径分别为0.1 m，0.15 m，0.1 m；轴密度、泊松比、弹性模量及剪切模量分别为 7.8×103kg／m3，0.3，2.1×1010Pa，8.076 9×1010Pa；橡胶轴承 Y，Z向总体刚度分布为2.62×106N·m，1.5×106N·m；轴系额定转速 0～100 r／min，取系统阻尼参数 α1＝0.1，β1＝1.2×10－6。采用四阶Runge－Kutta法求解系统非线性动态响应，时间步长1×10－5。

3.2 求解结果及分析

3.2.1 轴系固有特性

利用以上系统参数通过有限元法求出系统固有频率、固有振型（包括弯曲、扭转振动）分别见表1、图4。图4中横轴为轴系沿纵向位置坐标，纵轴为归一化的振型位移。3.2.2 摩擦参数影响

表1 系统前四阶固有频率Tab.1 The first four natural frequencies

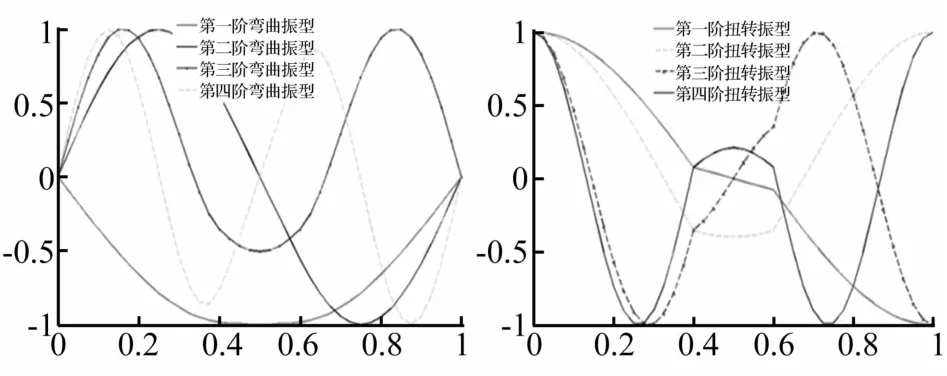
图4 系统前四阶固有振型Fig.4 The first four modes of the shaft

无特别说明，轴承座倾角均为零。不同摩擦参数时距轴系左端0.45 m轴承－轴颈接触处非线性动力学响应见图5。图5（a）的摩擦系数较小，对初始扰动，轴系激发的各阶模态振幅值逐渐减小，表明系统稳定；图5（b）、（d）的摩擦系数相对较大，由初始扰动激发的轴系各阶模态振幅值逐渐增大，当扭转振动角速度大小接近轴系转动角速度时，系统发生自激振动。比较图5（b）、（d）知，增大摩擦系数可缩短系统发生自激振动时间。图5（c）为对产生自激振动的时域响应的频域分析。此时系统的自激频率主要为扭转第二阶频率。计算发现该频率对应的阻尼较小，而模态响应相对较大。因此，第二阶模态更易被激发，与仿真结果吻合。图5（e）为系统发生自激振动时系统所受摩擦力矩。该摩擦力矩表现出的周期性负阻尼效应为导致系统模态失稳重要因素之一。该机理与文献［9］类似。

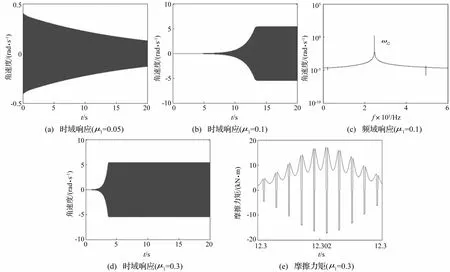
图5 距轴系左端0.45 m轴承－轴颈接触处非线性动态响应（μ0＝0.01，β0＝1，N′＝100 kN，n＝50 r／min）Fig.5 The nonlinear dynamic response at the 0.45 m bearingshaft neck contact point

3.2.3 转速及接触力影响

系统在不同转速、接触力下非线性动态响应见图6、图7。比较图6（a）、图5（b）、图6（c）看出，转速越快系统越不易发生模态失稳。对低速条件的时域响应进行频域分析，对比图5（c）、图6（b）看出，转速越低系统激发的扭转频率越多。除第二阶扭转振动频率外，在212 Hz，5 572 Hz附近有明显峰值，分别对应第一阶弯曲振动频率、第三阶扭转振动频率。比较图7（a）、图5（b）、图7（b）看出，接触力越大系统越易发生模态失稳。失稳时接触力越大系统达到稳定自激振动所需时间越少。图6、图7结果表明，相同条件下系统低速、重载时易发生自激振动。

图6 距轴系左端0.45 m轴承－轴颈接触处不同转速下非线性动态响应（μ0＝0.01，μ1＝0.1，β0＝1，N′＝100 kN）Fig.6 The nonlinear dynamic response at the 0.45 m bearingshaft neck contact point under different rotational speed

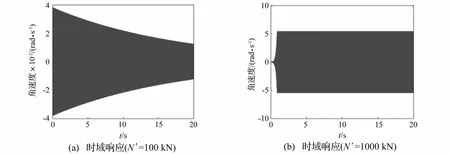
图7 距轴系左端0.45 m轴承－轴颈接触处不同接触力下非线性动态响应（μ0＝0.01，μ1＝0.1，β0＝1，n＝500 r／min）Fig.7 The nonlinear dynamic response at the 0.45m bearingshaft neck contact point under different contact force

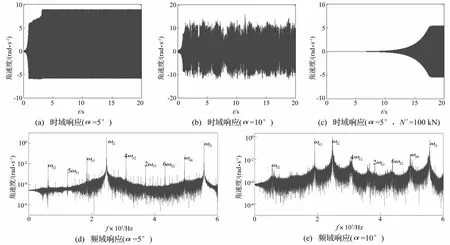
图8 距轴系左端0.45 m轴承－轴颈接触处不同倾斜状态下非线性动态响应（μ0＝0.01，μ1＝0.1，β0＝1，n＝50 r／min，N′＝1 000 kN）Fig.8 The nonlinear dynamic response at the 0.45 m bearingshaft neck contact point under different bearing inclination angle

3.2.4 轴承倾斜影响

以上分析均为轴承无倾斜，接触力均匀施加于中间轴段；但轴承倾斜与否亦为系统发生自激振动的重要因素。系统在不同轴承倾角条件下非线性动态响应见图8。参数选择满足条件N′≥kylztanα／2，以保证轴承下部分与轴颈间紧密接触。比较图7（b）、图8（a）、（b），当轴承倾斜时系统更易发生自激振动，且振幅值明显高于轴承无倾斜时振幅值。对比图8（a）、（b）看出，随轴承倾角增大系统发生模态失稳达到稳定振幅后出现周期性波动。由图8（c）看出，轴承发生倾斜时对相同摩擦系数及转速，减小接触力仍会发生自激振动。对产生自激振动的时域响应进行频域分析见图8（d）、（e）。此时系统激发出多阶弯曲、扭转模态频率及其倍频。

4 结 论

（1）通过仿真表明，轴系在低速、重载条件下，摩擦激励可能激发系统某些固有模态，引发自激振动。而摩擦负阻尼特性为引发轴系模态失稳的重要原因。

（2）除摩擦负阻尼效应外，轴系转速、接触力及轴承倾斜等均为系统发生自激振动的重要影响因素。转速降低、接触力增大及轴承倾斜角度加大，系统越易发生自激振动；轴承发生倾斜时振幅值明显高于轴承未倾斜时振幅值。

（3）本文所用分布式支承方式对轴承的建模，可为分析轴承分布支承力及轴承倾斜对轴系自激振动影响提供可能。

［1］姚世卫，杨俊，张雪冰，等.水润滑橡胶轴承振动噪声机理分析与试验研究［J］.振动与冲击，2011，30（2）：214－216.YAO Shiwei， YANG Jun， ZHANG Xuebing， et al.Vibration and noisemechanism analysis and tests for waterlubrication rubber bearings［J］.Journal of Vibration and Shock，2011，30（2）：214－216.

［2］王隽，杨俊，张雪冰，等.水润滑橡胶轴承振动噪声特性分析［J］.节能技术，2012，30（5）：392－396.WANG Jun，YANG Jun，ZHANG Xuebing，et al.Analysis of frictional noise of water lubricated rubber bearings［J］.Energy Conservation Technology，2012，30（5）：392－396.

［3］Peng E，Liu Z，Zhou X，et al.Study on nonlinear frictioninduced vibration in waterlubricated rubber stern tube bearings［J］.The Open Mechanical Engineering Journal，2012，6：140－147.

［4］段芳莉.橡胶轴承的水润滑机理研究［D］.重庆：重庆大学，2002.

［5］余江波.水润滑复合橡胶轴承摩擦学性能研究［D］.重庆：重庆大学，2002.

［6］Peng E G，Liu Z L，Tian Y Z，et al.Experimental study on frictioninduced vibration of waterlubricated rubber stern bearing at low speed［J］.Applied Mechanics and Materials，2011，44（47）：409－413.

［7］姚世卫，王娟，王隽，等.水润滑橡胶轴承摩擦行为及试验研究［J］.舰船科学技术，2009，31（12）：32－35.YAO Shiwei，WANGJuan，WANGJun，et al.Vibration and noise generation theory and experiment of waterlubricated rubber bearings［J］.Ship Science and Technology，2009，31（12）：32－35.

［8］Simpson T A，Ibrahim R A.Nonlinear frictioninduced vibration in waterlubricated bearings［J］. Journal of Vibration and Control，1996，2（1）：87－113.

［9］ Krauter A I.Generationofsqueal／chatter in waterlubricated elastomeric bearings［J］.Journal of Lubrication Technology，1981，103（3）：406－413.

［10］Mihajlovic N，Van De Wouw N，Rosielle P C J N，et al.Interaction between torsional and lateral vibrations in flexible rotor systems with discontinuous friction［J］.Nonlinear Dynamics，2007，50（3）：679－699.

［11］张振果，张志谊，陈锋，等.摩擦激励下螺旋桨推进轴系弯扭耦合振动研究［J］.机械工程学报，2013，49（6）：74－80.ZHANG Zhenguo， ZHANG Zhiyi， CHEN Feng，et al.Research on the coupling between torsion and lateral vibrations in propellershaft system with friction［J］.Journal of Mechanical Engineering，2013，49（6）：74－80.

［12］张振果，张志谊，王剑，等.螺旋桨推进轴系摩擦自激扭转振动研究［J］.振动与冲击，2013，32（19）：161－167.ZHANG Zhenguo， ZHANG Zhiyi， WANG Jian，et al.Frictioninduced selfexcited vibration in propeller shaft systems［J］.Journal of Vibration and Shock，2013，32（19）：161－167.

［13］温诗铸，黄平.摩擦学原理［M］.北京：清华大学出版社，2002.

［14］Vollebregt E A H，Schuttelaars H M.Quasistatic analysis of twodimensional rolling contact with slipvelocity dependent friction［J］.Journal of Sound and Vibration，2012，331（9）：2141－2155.