基于威布尔分布及最小二乘支持向量机的滚动轴承退化趋势预测

陈 昌，汤宝平，吕中亮

（重庆大学 机械传动国家重点实验室，重庆 400030）

准确预测滚动轴承退化趋势对预防设备性能退化及失效意义重大。滚动轴承趋势预测关键即建立合适的性能退化指标及预测模型［1］。单个时频域特征指标［2－4］对早期故障敏感程度低，不能较好确定初始损伤时间。融合时频域指标［5－7］虽能全面反应轴承退化信息，但会增加运算的复杂程度。因不同类型故障的发生时间具有间歇性，对振动数据进行统计分析可避免故障类型误诊断［8］。文献［8－9］提取的威布尔分布均值、方差及极大似然函数负值作为状态特征信息识别轴承故障及故障类型，能较好刻画轴承的运行状态；但该统计量对轴承故障发展的灵敏性较差，而威布尔分布形状参数值对轴承运行状态变化较敏感，且能随轴承故障的发展呈明显上升趋势，故用威布尔分布形状参数作为性能退化指标。

趋势预测另一重要步骤为在确定性能退化指标后建立可靠的预测模型。文献［5，10－11］分别采用神经网络及灰色理论建立预测模型，预测滚动轴承的退化趋势。由于灰色理论缺乏平稳性检验，且忽略非平稳信息，出现较大预测误差。神经网络存在局部极小、小样本推广能力差等难解决问题。而最小二乘支持向量机［6］在小样本、高维、非线性等数据空间下具有较好的泛化能力，但其核参数σ及正规化参数γ对模型预测、推广性能影响较大，用粒子群算法优化核参数及正规化参数可明显提高预测精度及预测结果的稳定性。

本文将威布尔分布形状参数与粒子群优化的最小二乘支持向量机相结合，提出轴承退化趋势预测新方法。该方法充分发挥威布尔分布形状参数在早期故障敏感度及粒子群优化的最小二乘支持向量机预测模型优势，预测精度较高。

1 轴承性能退化指标

滚动轴承出现早期故障时其信息较易淹没于噪声信号中。希尔伯特变换［8］对轴承早期故障信息提取效果良好，故在提取轴承性能退化指标前先对振动数据作希尔伯特变换。对正常轴承及不同类型故障轴承而言，振动信号的包络值均可用威布尔分布建立模型［12］。威布尔分布概率密度函数［8］为

据牛顿迭代法求参数β，η。由于极大似然方法估计参数时存在误差，采用修正方法［13］，修正形状参数β可减少估计误差。修正公式为

式中：N为数据长度；βU为修正值；β为估计值。

由Cincinnati大学实测的滚动轴承全寿命实验数据计算威布尔分布的两模型参数、极大似然函数负值（nLog）［9］及威布尔分布均值（mu）与方差（Std）［8］，同时计算时域特征值（均值、峭度、波形指标、裕度指标）、频域特征值（均值频率、均方根频率）、融合指标（主成分分析 （PCA）第一主成分（PC1）［6］）。各特征值趋势曲线见图1、图2。由两图看出，威布尔分布均值及方差、尺度参数η及时域特征量均值、均方根频率不随故障发展呈上升趋势，不适合作轴承的性能退化指标。而波形指标、裕度指标虽呈现一定退化上升趋势，但指标总体信息较嘈杂，亦不适合作轴承的衰退性能指标。峭度、均值频率指标随故障发展呈较好的上升趋势，但在700点后才呈现上升趋势，此时轴承已趋向严重失效状态，不能反应轴承的早期故障。威布尔分布形状参数及极大似然函数负值在约500点呈上升趋势，与PC1退化趋势相近，能较好、全面反映轴承的退化趋势，且对早期故障的敏感度更高。与极大似然函数负值相比，威布尔分布形状参数在500点前基本趋于一直线，整体趋势较纯净。故选威布尔分布的形状参数作为性能退化指标。

图1 全寿命轴承信号时、频域指标Fig.1 The time and frequency domain character indicators of the whole life bearing test signal

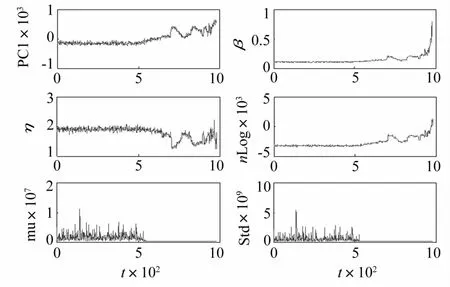
图2 全寿命轴承信号统计指标Fig.2 The statistical indicators of the whole life bearing test signal

用威布尔分布形状参数作为轴承性能退化指标具有两点优势：① 计算简单；② 对轴承早期故障的敏感程度高，能较好反映轴承性能退化趋势。

2 基于粒子群优化的最小二乘支持向量机

2.1 最小二乘支持向量机理论

最小二乘支持向量机将最小二乘线性理论引入支持向量机，为标准支持向量机理论的扩展利用［6］。LSSVM定义与标准支持向量机不同的约束函数，并据拉格朗日函数及KKT条件将不等式约束化成等式约束，构成LSSVM优化模型为

式中：ω为权向量；γ为正则化参数或曰惩罚因子，其可决定对超出误差样本的惩罚程度，为支持向量机拟合程度与推广能力的平衡参数；b为偏差向量；ξi为松弛变量，表明实际对象对逼近函数在样本数据点的误差期望。

由式（5）得最小二乘支持向量机的拉格朗日函数为

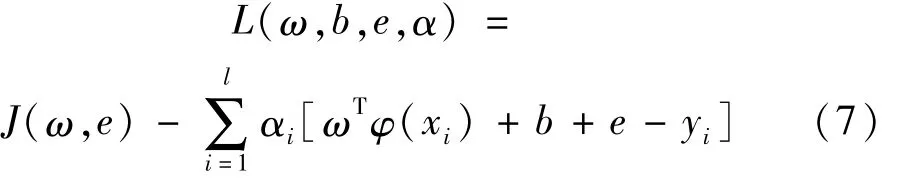
式中：αi为拉格朗日乘子。

对式（7）进行优化，即 L（ω，b，e，α）分别对 ω，ei，b，αi求偏导数，并令偏导数为零。消去变量ω，e得

用径向基函数（RBF）作为核函数，表达式为

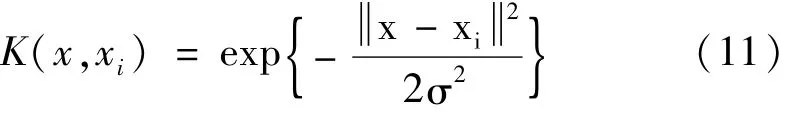
式中：σ为核函数宽度。

2.2 粒子群优化的最小二乘支持向量机

LSSVM虽能较好解决小样本、非线性、局部极小点等问题，但实际应用中LSSVM核参数σ及正规化参数γ对其预测推广性能影响较大，因此用LSSVM预测时需对核参数及正规化参数进行优化。LSSVM优化方法较多，如交叉验证法、梯度下降法、遗传算法、粒子群算法等。粒子群算法具有能获取全局最优结果、收敛速度快、鲁棒性好、寻优能力强及编程易实现等优点［14］。故选粒子群算法优化最小二乘支持向量机的模型参数。

选均方误差（MSE）作为PSO算法的粒子适应度函数，表达式为

式中：n为训练样本个数；yi为实际值；y＾i为预测值。

PSO优化LSSVM算法中，将寻优目标参数γ、σ作为粒子，均方误差作为适应度函数，算法基本步骤为：① 初始化种群参数，包括种群规模、最大粒子数及终止条件等；随机设置参数γ、σ的初始位置及速度。② 作一次LSSVM训练，计算训练样本均方误差作为粒子的初始适应值。③ 更新速度及位置向量。④ 将更新的γ、σ值重新代入SVM模型，并据②重新训练，保存其输出结果，计算粒子的适应值。⑤ 将④中所得适应值与当前粒子适应值比较，若优于当前粒子适应值，则更新当前粒子适应值，并将参数γ、σ更新为与④中相对应的γ、σ。⑥ 判断是否满足停止条件，满足则终止迭代，否则返回③。⑦ 输出最优解，结束算法。

3 基于威布尔分布形状参数及粒子群优化的LSSVM轴承趋势预测

本文用威布尔分布形状参数作为性能退化指标，利用LSSVM作趋势预测。由于早期故障易淹没于振动信号中，造成趋势预测精度下降，故引入Hilbert变换对振动信号进行预处理。对Hilbert处理后全寿命振动数据提取威布尔分布形状参数，将其作为性能退化指标，输入LSSVM模型中预测轴承的退化趋势；用粒子群算法优化LSSVM的核参数σ及正规化参数γ提高预测精度。具体流程见图3：

（1）先对振动数据作Hilbert变换，再计算其威布尔分布的形状参数；

（2）将该形状参数作为性能退化指标，输到LSSVM模型中；

（3）将粒子群优化的核参数及正规化参数作为LSSVM模型参数建立预测模型，获取预测结果；

（4）按步骤（1）、（2）处理轴承全寿命实验数据，将结果输入预测模型中进行预测。

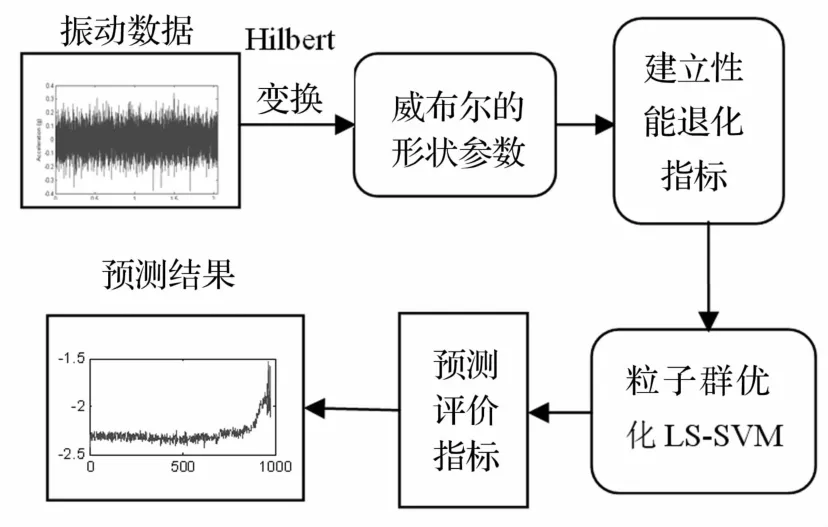
图3 滚动轴承退化趋势预测流程Fig.3 The flowchart of the rolling bearing degradation trend forecasting process

4 基于轴承全寿命实验验证

用实测的滚动轴承全寿命数据［15］进行验证，全寿命实验装置及采集仪器布置见图4。轴承实验台转轴上安装4个Rexnord公司ZA－2115双列滚子轴承，交流电机通过带传动2 000 r／min恒定转速带动转轴旋转，实验时为轴承施加6 000 lbs径向载荷。每个轴承的X，Y向各安装一PCB 353B33加速度传感器，采样频率20 kHz，采样间隔10 min，采样长度20 480点。轴承持续运行7天，直到失效。

图4 轴承全寿命实验装置及采集仪器布置图［15］Fig.4 The whole life bearing test equipment

选威布尔分布形状参数作为轴承性能退化指标，该指标部分数据用于训练LSSVM模型并完成预测，将所得预测值与实际性能退化指标进行对比分析。确定性能退化指标后利用粒子群算法优化最小二乘支持向量机的核参数σ及正规化参数γ。粒子群数目设为20，最大迭代次数设为200，加速因子 c1，c2均设为1.5，粒子群算法优化最小二乘支持向量机核参数σ为24、正规化参数γ为94.5，用此两模型参数构建最小二乘支持向量机模型进行训练及预测。在700点之前轴承基本处于正常运行状态。因此用700～900点进行训练，900点后的数据作预测。为评价预测结果的准确性，用平均相对误差作为预测效果［1］的评价指标。

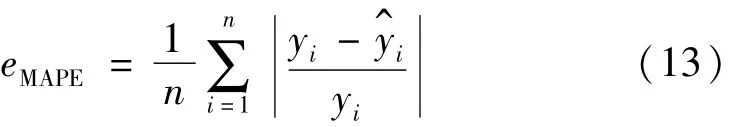
式中：n为测试数据个数；yi为实际值；y＾i为预测值。

预测中预测模型保持不变，将预测结果作为输入进行下一步预测，获得预测结果后再次作为输入进行下一步预测，如此循环迭代实现预测。该预测方法优势在于预测结果可作为输入用于预测之后结果，可用于新数据较难获取情况。预测数据部分结果见图5。由图5看出，20步预测范围内预测曲线与实际性能退化曲线较接近，平均相对误差为0.158 2。与实测数据作为输入预测方法对比知，平均相对误差为0.114 9。通常轴承的全寿命实验数据较难获取，用预测数据作为下一步输入可使预测更具实用性、推广性。

为进一步验证形状参数作为退化指标方法的准确性及整体算法各环节的必要性，进行对比验证，比较预测结果的平均相对误差值：① 峭度作为性能退化指标，PSO优化LSSVM建立预测模型；② 均方根值作为性能退化指标，PSO优化LSSVM建立预测模型；③ 裕度指标作为性能退化指标，PSO优化LSSVM建立预测模型；④ PC1作为性能退化指标，PSO优化LSSVM建立预测模型；⑤ 形状参数作性能退化指标，人为固定SVM模型参数建立预测模型；⑥ 形状参数作性能退化指标，粒子群算法优化SVM模型参数建立预测模型；⑦ 形状参数作性能退化指标，固定LSSVM的模型参数建立预测模型；⑧ 形状参数作性能退化指标，采用神经网络建立预测模型。对比结果见图6及表1。

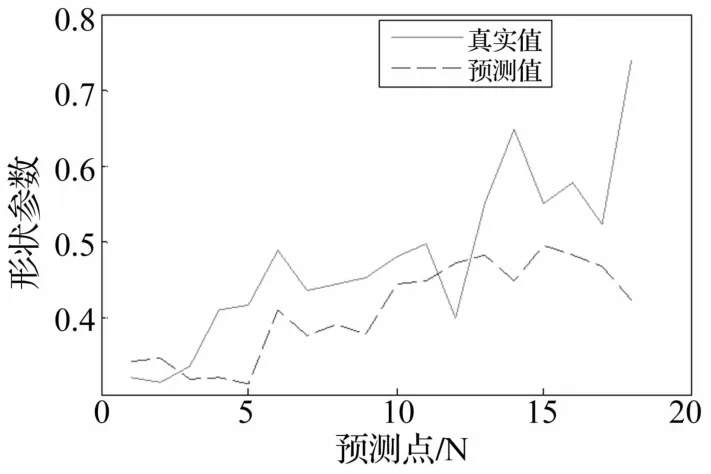
图5 滚动轴承趋势预测曲线与实际状态趋势曲线Fig.5 The actual state trend curve and the forecast trend curve

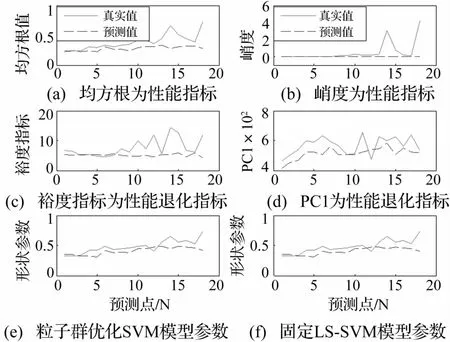
图6 其它方法趋势预测曲线与实际状态趋势曲线Fig.6 The forecast trend curve obtained by other methods and the actual state trend curve

由图5、图6、表1看出，形状参数作为性能退化指标能较好反应轴承的退化趋势，且预测效果优于峭度、裕度指标及均方根值作为性能退化指标的预测效果。而基于峭度、裕度指标及均方根等特征指标由于对早期故障不敏感，导致预测结果出现较大误差。形状参数作为性能退化指标的预测效果与PC1预测效果相近，且无需多特征信息融合，可减少计算复杂程度及运算量。采用PSO优化LSSVM建立预测模型预测效果优于PSO优化SVM预测效果，采用PSO优化LSSVM模型参数预测效果优于固定LSSVM模型参数预测效果。表明减少模型参数个数，合理选择模型参数可减少预测误差、提高预测精度。因此，威布尔分布形状参数作为性能退化指标能有效反映轴承性能退化趋势，预测精度较高。

表1 各方法预测结果与实际性能退化指标间误差比较Tab.1 The prediction error comparison of different methods

工程实际中轴承趋势预测通常用一个轴承训练建模预测另一同型号、同工况轴承的退化趋势。试验中2、3号为同型号、工况类似的两滚动轴承，用2号轴承训练模型预测3号轴承退化趋势，形状参数作为性能退化指标所得3号轴承预测结果的平均相对误差为0.235 8，而PC1作性能退化指标所得平均相对误差为0.522 9。反之，用3号轴承训练模型预测2号轴承退化趋势，形状参数作为性能退化指标所得2号轴承的平均相对误差为0.1496，而PC1作性能退化指标所得平均相对误差为0.271 4。实验表明，威布尔分布的形状参数作性能退化指标预测结果最优。

5 结 论

（1）本文通过分析常用时频域特征作为性能退化指标存在问题，提出采用威布尔分布的形状参数作为性能退化指标，在识别早期故障的同时亦能较好预测轴承的性能退化趋势。

（2）为获得更准确预测结果，选粒子群算法优化LSSVM模型参数，利用粒子群算法的寻优能力提高LSSVM预测精度。

（3）通过对比分析全寿命振动数据，表明本文所提趋势预测方法的有效性及各环节间关联性，能充分发挥各部分优势，实现较高精度的退化趋势预测。

［1］申中杰，陈雪峰，何正嘉，等.基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测［J］.机械工程学报，2013，49（2）：183－189.SHEN Zhongjie，CHEN Xuefeng，HE Zhengjia，et al.Remaining life predictions of rolling bearing based on relative features and multivariable support vector machine［J］.Chinese Journal of Mechanical Engineering，2013，49（2）：183－189.

［2］Gebraeel N，Lawley M，Liu R，et al.Residual life predictions from vibrationbased degradation signals：a neural network approach［J］.Industrial Electronics，IEEE Transactions on，2004，51（3）：694－700.

［3］Shao Y，Nezu K.Prognosis of remaining bearing life using neural networks［J］.Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2000，214（3）：217－230.

［4］Janjarasjitt S，Ocak H，Loparo K A.Bearing condition diagnosis and prognosis using applied nonlinear dynamical analysis of machine vibration signal［J］.Journal of Sound and Vibration，2008，317（1／2）：112－126.

［5］奚立峰，黄润青，李兴林，等.基于神经网络的球轴承剩余寿命预测［J］.机械工程学报，2007，43（10）：137－143.XI Lifeng，HUANG Runqing，LI Xinglin，et al.Residual life predictions for ball bearing based on neural networks［J］.Chinese Journal of Mechanical Engineering，2007，43（10）：137－143.

［6］刘宝英，杨仁刚.基于主成分分析的最小二乘支持向量机短期负荷预测模型［J］.电力自动化设备，2008，28（11）：13－17.LIU Baoying，YANG Rengang.Shortterm load forecasting model based on LSSVM with PCA［J］.Electric Power Automation Equipment，2008，28（11）：13－17.

［7］Liao H，Zhao W，Guo H.Predicting remaining useful life of an individual unit using proportional hazards model and logistic regression model［C］.Reliability and Maintainability Symposium，2006：127－132.

［8］Jiménez G A，Munoz A O，DuarteMermoud M A.Fault detection in induction motors using Hilbert and wavelet transforms［J］.Electrical Engineering，2007，89（3）：205－220.

［9］Abbasion S，Rafsanjani A，Farshidianfar A，et al.Rolling element bearings multifault classification based on the wavelet denoising and support vector machine［J］.Mechanical Systems and Signal Processing，2007，21（7）：2933－2945.

［10］Yan J，Guo C，Wang X.A dynamic multiscale Markov model based methodology for remaining life prediction［J］.Mechanical Systems and Signal Processing，2011，25（4）：1364－1376.

［11］徐东，徐永成，陈循，等.基于 EMD的灰色模型的疲劳剩余寿命预测方法研究［J］.振动工程学报，2011，24（1）：104－110.XU Dong，XU Yongcheng，CHEN Xun，et al.Residual fatigue life prediction based on grey model and EMD［J］.Journal of Vibration Engineering，2011，24（1）：104－110.

［12］龙凯，李刚成.基于 Hilbert变换与威布尔分布的轴承早期故障诊断［J］.科学技术与工程，2010，10（17）：4163－4167.LONG Kai，LI Gangcheng.A method of incipient fault diagnosis for rolling bearing based on hilbert transform and weibull distribution ［J］. Science Technology and Engineering，2010，10（17）：4163－4167.

［13］Ross R.Formulas to describe the bias and standard deviation of the mlestimated weibull shape parameter［J］.Dielectrics and Electrical Insulation， IEEE Transactions on，1994，1（2）：247－253.

［14］Eberhart R，Kennedy J.A new optimizer using particle swarm theory［C］.Pro Sixth International Symposium on Micro Machine and Human Science，Japan，1995：39－43.

［15］Lee J，Qiu H，Yu G，et al.Rexnord technical services，“bearing data set”［R］.IMS，University of Cincinnati，NASA Ames Prognostics Data Repository，＜http：／／ti.arc.nasa. gov／project／ prognosticsdatarepository ＞， NASA Ames，Moffett Field，CA，2007.