基于改进应力变化率法的空间杆系结构鲁棒性分析
刘国光,武志玮,刘慧源,谭 振
(中国民航大学 机场学院,天津 300300)
鲁棒性是结构不产生与起因不相称破坏的能力,包括结构抗倒塌性能、冗余度、敏感性及易损性等评价指标[1]。受构件截面类型和材料力学性能影响,空间杆系结构的鲁棒性与传统混凝土结构差异较大。在实际工程应用中多采用变换荷载路径法分析结构可能因局部敏感性强的易损构件破坏所造成的结构倒塌,如:蔡建国等[2]将结构倒塌分析方法归纳为五类,分别是:基于刚度、能量、强度、敏感性和基于经验及理论,并在新广州站索拱结构屋盖体系分析中采用变换荷载路径法研究了空间结构静力分析结果的动力放大系数[3-4]。赵楠等[5]在克拉玛依科技博物展览馆工程张弦梁结构抗连续倒塌设计中运用了抽柱法,考察了中间榀拉索失效时张弦梁结构的抗连续倒塌性能。周健等[6]运用直接拆除构件法分析了虹桥B3结构单元的鲁棒性,证明了结构具有较高的可靠度。然而,应用变换荷载路径法分析结构鲁棒性最大的难题在于如何确定杆件移除顺序,需要通过专家对构件的重要性进行排序并对构件拆除后的影响给出相应权重,对于空间杆系结构而言,此类可参考的因素集和权重集尚未有公认指标。
为建立空间杆系结鲁棒性的评价标准,吕大刚等[7]基于备用荷载路径法分析了结构连续倒塌鲁棒性,验证了该方法可有效分析结构鲁棒性且分析损伤强度更方便。丁阳等[8]利用显式中心差分法提出了适用于空间网架结构的实时删除构件的瞬时移除构件法。王磊等[9]利用了显示积分算法研究了动力效应对低冗余度结构体系的极限承载力影响。郑阳等[10]采用了非线性动力分析方法,引入柱的特征移除系数μ定量识别重要构件。上述诸多评价标准都是围绕变换荷载路径法通过移除杆件模拟结构破坏过程分析结构鲁棒性。为便于工程应用、降低主观因素对评价结果的影响,杜文风等[11]应用应力变化率法研究结构局部失稳,给出了结构易损性的量化指标,验证了其可靠性和有效性,并采用了蒙特卡洛法和拉丁超立方抽样法及增量动力时程分析方法,研究了预应力对张弦梁结构易损性的影响[12-13],收到了较好效果。但是,已有研究表明,在结构发生变形失稳前应力变化率的跳跃并不显著,当若干根杆件应力变化率水平接近时,现有应力变化率法可判断结构是否失效却难以预测结构失效模式。
为发挥应力变化率法在确定杆件失效模式方面的高效性和客观性,结合空间杆系结构受力特点,引入杆件关键系数改进了应力变化率法,用以判断杆件移除顺序及预测结构失效模式。通过对静力阶跃荷载和地震作用下某一单层星型穹顶结构的算例分析,讨论了改进应力变化率法在判断杆件移除顺序和预测结构失效模式方面的功能。然后应用改进应力变化率法对一新型张弦桁架结构进行了结构鲁棒性分析,利用敏感性分析方法和冗余度理论,研究了局部破坏对构件受力敏感性的影响,并同传统张弦桁架结构进行了横向对比,验证了该新型张弦桁架结构的可靠性,对其进行的动力分析结果表明,当两根杆件的应力变化率水平接近时,通过杆件关键系数可有效判断杆件移除顺序,从而判断结构失效模式。
1 基于改进应力变化率法的结构鲁棒性预测方法
1.1 杆件失效模式预测
在应力变化率法中,定义某一时刻t杆件总应变能为Π,其表达式如式(1)所示。

其中 μ为应变能密度,μ=σijεij/2,当处于弹性状态时σij=Cijεij,对 总 应 变 能 求 微 分 得 到 dΠ =其中Cij为弹性模量矩阵分量。杆系结构应用有限元法划分单元后,总应变能可写成dΠ =当结构发生动力失稳时,总应变能发生突变,dΠ会突然跳跃到一个相对大值,而应力向量σ是一个有界向量,因此,当应力变化率然跳跃到一个相对很大值时,可判定杆系结构发生动力失稳[12]。应力变化率法可有效判断杆系结构的杆件是否处于破坏状态,但由于在杆件破坏前应力变化率波动较小,难以预测杆件破坏,无法在杆件破坏前进行预警以供撤离或结构抢修,以避免发生局部破坏乃至连续倒塌。因此,改进应力变化率法引入了杆件关键系数K[10],可有效地放大杆件破坏前若干荷载步所对应的应力变化率,其计算公式如式(2)所示。

其中n指与待判断杆件相连(包括待判断杆件)的杆件数,Si指第i根杆件内力,Ri指第i根杆件的极限抵抗力,K反映了周围杆件在该根杆件破坏过程中的综合作用。由于K为小数,在应用改进应力变化率法时,需要将由改进应力变化率法获得的应力变化率曲线乘以放大系数,使得利用两种方法获得的杆件应力变化率具有相同的起始值,再比较不同荷载步的应力变化率跳跃幅度,实现根据周边杆件内力变化预测待判断杆件失效模式的目的。
1.2 结构可靠性分析方法
单根结构构件对整个结构抗连续性倒塌能力的影响与结构冗余度密切相关,并通过敏感性指标(SI)反映,其计算方法如式(3)所示[12]。

其中,0表示构件初始状态下的承载力系数,d表示构件失效后的承载力系数。当SI→0时,表明该构件损坏对结构连续性倒塌无直接影响(即非敏感构件);当SI→1时,表明该构件损坏会引起结构连续性倒塌(即敏感构件);当SI介于二者之间时,SI与R成反比例关系,可利用敏感性指标的变化趋势分析结构冗余度变化,从而评价结构抗连续性倒塌能力。采用改进应力变化率法分析某根构件损坏后结构剩余构件应力变化,获得第i个构件的敏感性指标关键是确定第i个构件的承载力系数SIi,j(见式(4))以评估结构鲁棒性。

其中,表示第i个构件初始状态的截面应力表示移除第j个构件后,第i个构件的截面应力表示第i个构件的材料许用应力,K表示杆件关键系数(见式(2))。
通过上述理论分析可见,将关键系数法引入应力变化率方法,反映了结构杆件内力和周边杆件约束力的共同作用,克服了传统应力变化率法仅针对单根杆件内力变化率判断杆件稳定性的局限;体现了局部失稳发生前相邻结构杆件协同工作效果,解决了传统应力变化率法在结构发生变形失稳前应力变化率变化不显著的问题,能用于计算结构局部失稳临界荷载,通过监测杆件内力对可能导致结构失稳的荷载工况进行预警;考虑了相邻拉杆和压杆的作用,客观、量化地判断杆件移除顺序,避免了传统应力变化率法中需要专家打分的主观判断方式,预测结构失效模式更符合结构受力特性。
引入关键系数法后计算得到的构件承载力系数SIi,j修正了传统敏感性指标SI仅考虑自身杆件承载力系数的缺点,考虑了局部杆件强度和稳定性共同作用,得到了杆件敏感性指标的数值结果,能更有效的评价空间杆系结构的局部稳定性、识别连续倒塌模式和评价结果抗联系倒塌能力,是分析结构鲁棒性的有效工具。下面通过两个算例对其可靠性及应用加以说明。
2 单层星型穹顶算例
2.1 有限元模型的建立
如图1和图2所示,单层星型穹顶结构杆件的弹性模量 E=3.03×109,泊松比 v=0.3,杆截面面积 A=0.000 317 m2,杆件密度为 50 g/cm3。利用通用有限元分析软件ANSYS建模进行数值模拟分析,杆件采用link8单元,六个支承节点为固定铰支座,其他节点为铰接。
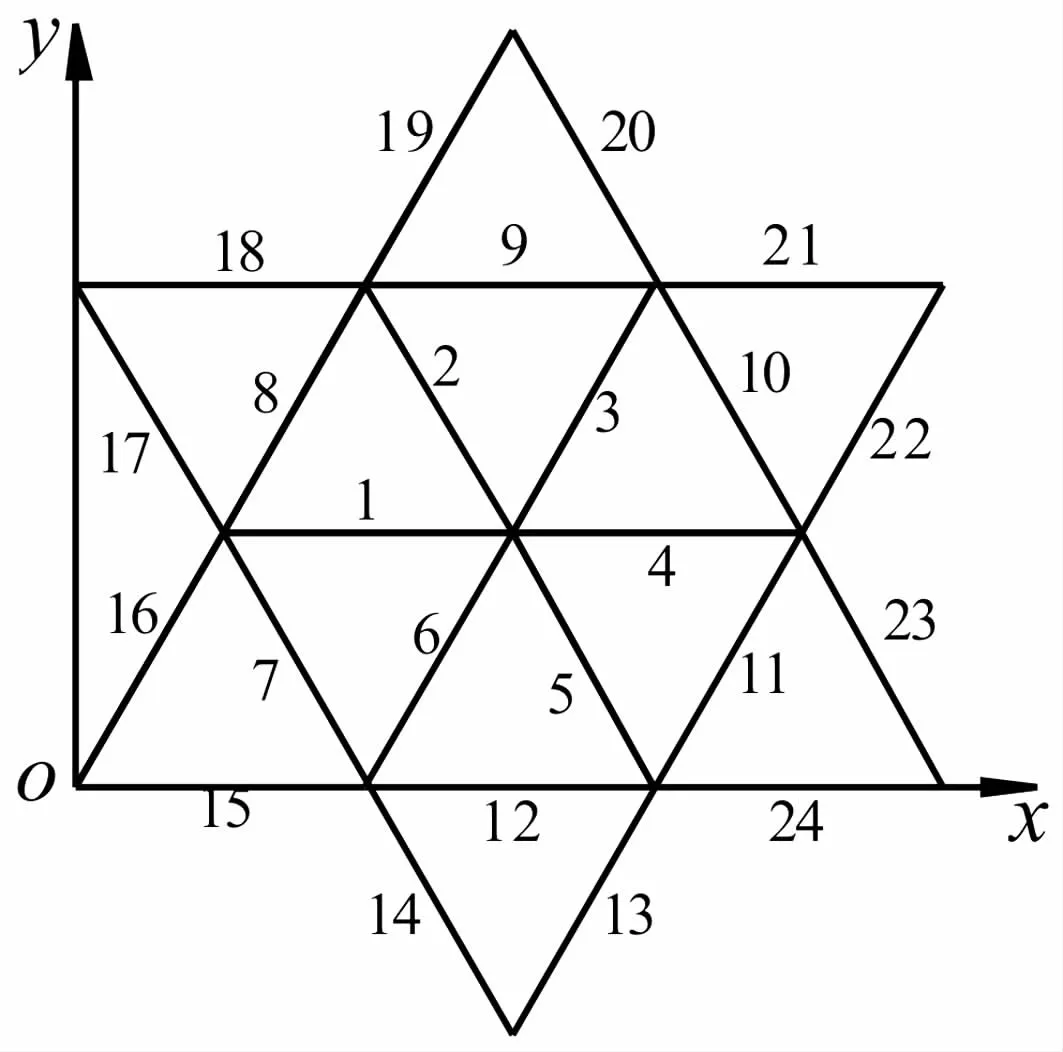
图1 单层星型穹顶结构平面图Fig.1 Plane drawing of single layer star dome

图2 单层星型穹顶结构立面图Fig.2 Vertical drawing of single layer start dome
2.2 不同荷载工况下杆件失效模式预测
分别计算均布阶跃荷载(起始荷载10 kN,荷载作用时间0.2 s,荷载增量为10 kN)、非均布阶跃荷载(荷载设计值 P=(x2+2y2)×100,荷载作用时间0.2 s,荷载增量为20 kN,其坐标系位置如图所示)和竖向地震作用(选取EL-Centro波的前300荷载步)下杆件应力变化率的改变情况,如图3所示。在验证经典应力变化率法判断结构失效模式准确性的同时,比较了改进应力变化率法对结构临界破坏发生前若干荷载步应力变化率幅值的放大作用。
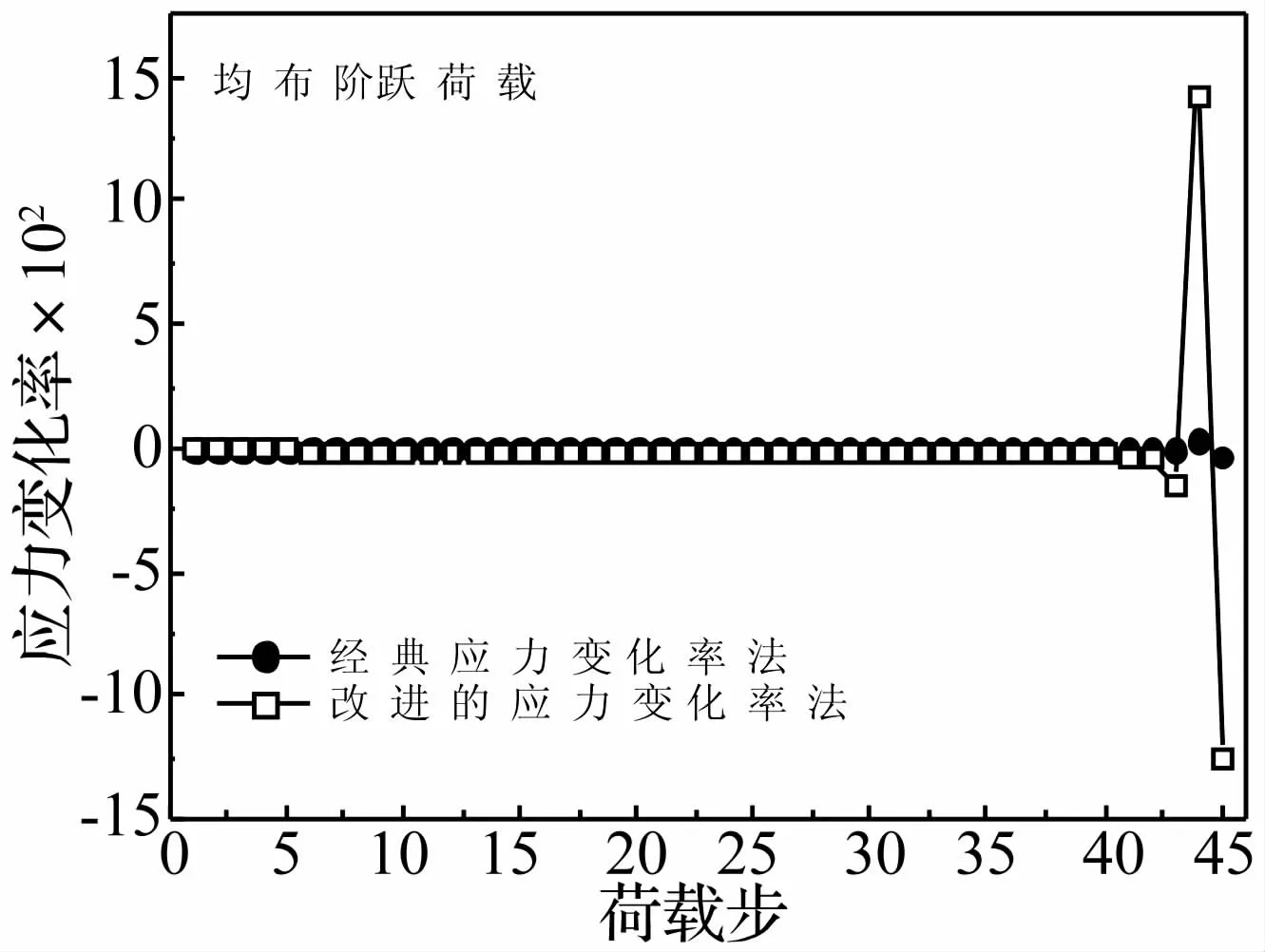
图3 两种方法计算的应力变化率曲线比较Fig.3 Comparisons of two stress ratemethods
由图3可知,尽管荷载工况不同,计算结果仍同文献[11]结论一致,验证了应力变化率法的可靠性。同时发现,在第42荷载步时,利用改进应力变化率法计算得到的应力变化率已经开始发生突变,而传统应力变化率法计算得到的应力变化率尚未突变;结构破坏发生前各荷载步的应力变化率跳跃更加显著,表明采用改进应力变化率法较传统应力变化率法在预测杆件破坏方面有了较大提高。图4和图5所示的单层星型穹顶结构在非均布阶跃荷载作用下的应力变化率曲线对比进一步验证了上述结论。
通过图6和图7所示的地震作用下杆件应力变化率曲线和结构失效模式可以发现,强震作用下结构发生大变形,穹顶失稳后在新平衡位置重新稳定、继续振动(如图6),对应的通过改进应力变化率法获得的应力变化率曲线在结构失稳发生前即产生较大跳跃(如图7),而传统应力变化率曲线变化则不显著,表明改进应力变化率法不仅适用于静力荷载作用,还适用于动力荷载作用,较传统应力变化率法有较大改进,且具有较好的预测杆件和结构破坏、失稳的能力。
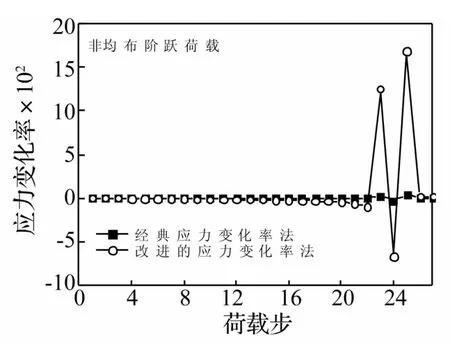
图4 非均布阶跃荷载作用下杆件1应力变化率曲线Fig.4 Stress rate curves of element 1 under non-uniform step load
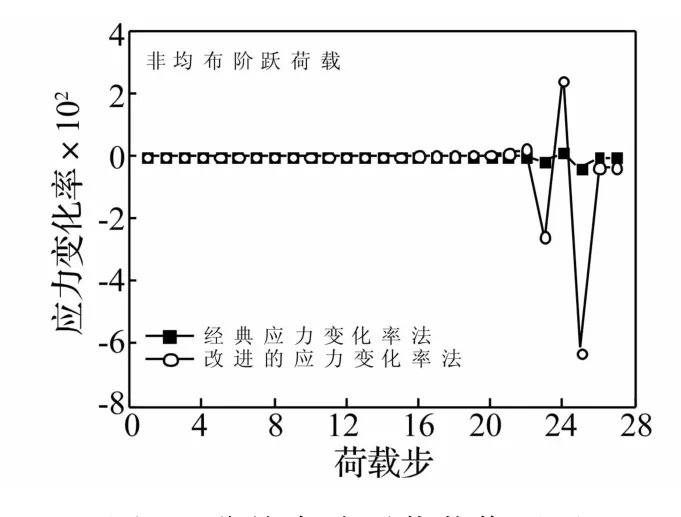
图5 非均布阶跃荷载作用下杆件7应力变化率曲线Fig.5 Stress rate curves of element 7 under non-uniform step load

图6 星型穹顶中央节点竖向位移曲线Fig.6 Vertical displacement of central node of star dome

图7 地震作用下杆件1应力变化率曲线Fig.7 Stress rate curve of element1 under seismic load
3 张弦桁架结构鲁棒性分析算例
张弦桁架结构是由索、上弦桁架及撑杆组成的全张拉空间杆系结构,近20年得到了广泛应用。但下弦索不但几何形状占用建筑净空,是敏感性最强的构件,其破坏还会导致结构整体倒塌。近几年,为提高张弦桁架结构鲁棒性,研究人员提出了若干种改进方法,如防连续倒塌的张弦结构[5],双索张弦桁架结构[14],改进悬臂型张弦梁结构[15],具有荷载缓和作用的张弦桁架结构[16]和高冗余度张弦桁架结构[17]等,研究重点是提高下弦索冗余度。下文利用改进应力变化率法分析了高冗余度张弦桁架结构不同类型杆件在多荷载工况下的敏感性,并同传统张弦桁架结构进行了对比,从数值解上证明了该新型张弦桁架结构具有更好的鲁棒性。同时,讨论了改进应力变化率法在识别空间杆系结构失效模式中的应用,利用关键系数法判断不同杆件应力水平接近时的移除顺序。
3.1 有限元模型的建立
为比较高冗余度张弦桁架结构与传统张弦桁架结构在抗连续性倒塌能力方面的改进,除拉索与撑杆数量布置不同外,张弦桁架跨度、尺寸、材料、边界条件、竖向撑杆与下弦拉索等完全相同,如图8和图9所示,各种构件的截面尺寸和材料特性如表1所示。

表1 张弦结构构件截面尺寸和材料特性Tab.1 Sectional and material properties of truss string structure
图8 张弦桁架结构平面布置图Fig.8 Horizontal drawing of TSS
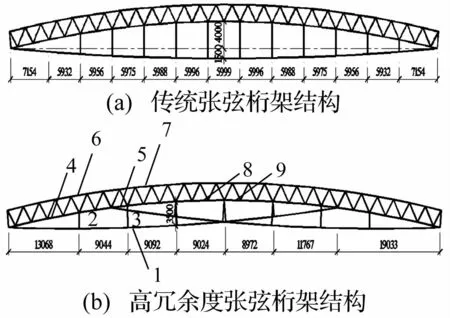
图9(a) 传统张弦桁架结构(b)高冗余度张弦桁架结构Fig.9(a)Traditional TSS(b)TSS of high redundancy
3.2 多荷载工况下结构敏感性分析
桁架梁杆件均采用Q345钢管,下弦索采用高强度钢绞线,屋面活荷载标准值取1.1 kN/m2,每榀桁架受荷面积810 m2,将屋面活荷载等效成节点集中力,分别加在桁架上弦节点上,平均每个节点8.5 kN。
利用有限元分析软件ALGOR计算了图2所示两种张弦桁架结构在设计荷载作用下初始状态的典型构件内力,如表2所示。可见,达到相同预起拱高度时高冗余度张弦桁架结构所需要下弦拉索预应力较传统张弦桁架结构下降17.5%,且能充分发挥上弦桁架杆件的力学性能,表明材料利用率较高。

表2 初始状态下结构部分构件内力Tab.2 Internal forces of elements under initial status
考虑移除一根拉索(工况1)和从跨边向跨中逐次移除竖向撑杆(工况2~工况7),分别计算在竖向静力荷载作用下结构构件的敏感性指标,以工况1为例,其计算结果如表3所示。
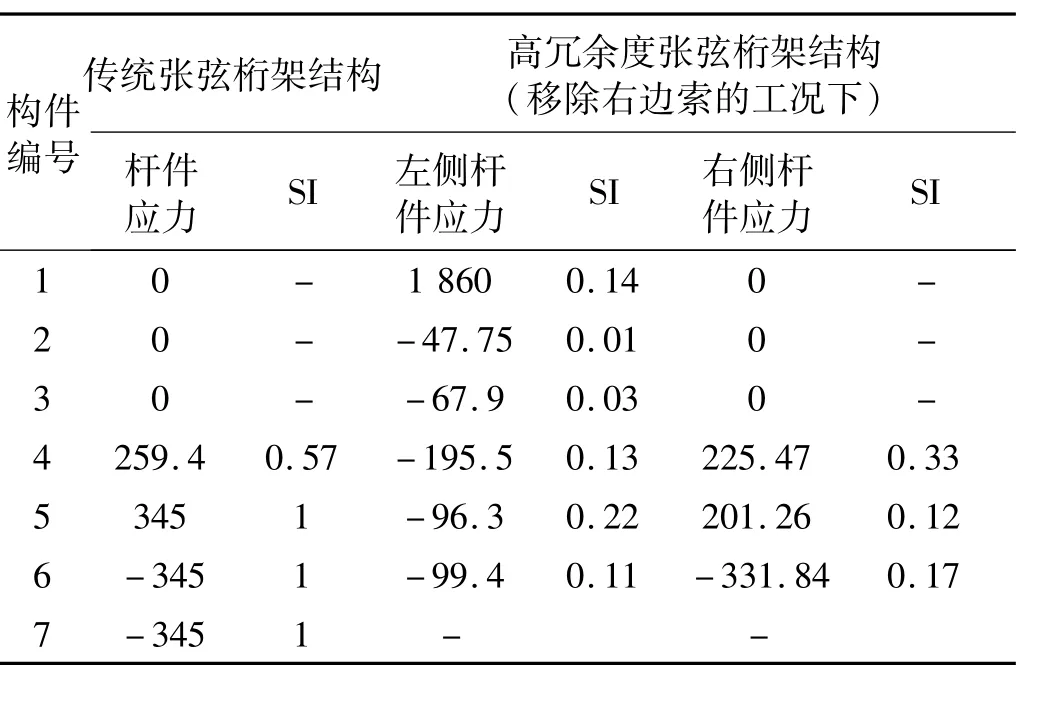
表3 初始状态下结构部分构件敏感性指标Tab.3 Sensitivity indexes of elements under initial status
由表3可知,当由于某种原因传统张弦桁架结构下弦索断裂后,竖向撑杆未发生破坏但成为附属构件不参与结构工作,其余内力由梁两端向跨中逐渐增大,传统张弦桁架结构的上弦杆件5~7立即破坏,杆件4随后破坏,表明结构破坏呈现连续性倒塌形式。
而高冗余度张弦桁架结构在单根下弦拉索破坏时,由于剩余索的约束作用,杆件压应力由梁两端向跨中逐渐减小,到跨中变为拉应力,在拉索破坏一侧个别杆件截面应力增加显著,但未达到其承载能力极限,大部分杆件截面应力变化并不明显,表明未破坏一侧下弦拉索的存在降低了其余构件对下弦拉索破坏的敏感性,提高了结构的冗余度,增加了结构的安全储备。对于工况2~工况8,经计算发现单根撑杆的破坏会引起结构内力重分布但不足以引起结构破坏。
通过改变下弦拉索的几何形状,降低了张弦桁架结构对建筑净空的限制,减少了相同预起拱形状时下弦拉索预应力值,显著提高了结构冗余度,克服了传统结构下弦拉索破坏后出现的连续倒塌破坏,为人员疏散提供了时间。证明了通过改进增强了高冗余度张弦桁架结构的鲁棒性,降低了各构件对下弦拉索破坏的敏感性,增强了结构抗连续性倒塌能力。
3.3 结构失效模式识别
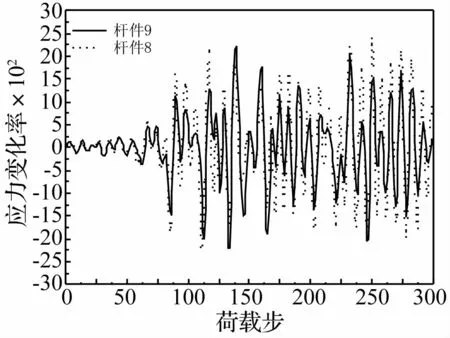
图10 两根杆件应力变化率曲线对比Fig.10 Stress rate comparisons of two elements

表4 部分杆件关键系数计算表Tab.4 Key coefficients of elements
利用应力变化率法逐一绘制杆件应力变化率曲线,发现在全部杆件中,杆件8和9的应力变化率最大且二者应力变化率幅值接近(如图10所示),难以判别二者谁先破坏。应用改进应力变化率法后分别计算杆件关键系数,如表4所示,可得杆件8的K值为0.42,杆件9的K值为0.36,从而可判别杆件8先于杆件9破坏。利用该方法逐一判断杆件移除顺序即可更准确获得结构失效模式。
通过算例分析可见,在杆件应力水平接近时,传统应力变化率法难以区分杆件移除顺序,引入关键系数法考虑相邻拉压杆贡献,可量化、直观判断杆件移除顺序,证明了改进应力变化率法在识别结构失效模式中应用价值。
4 结 论
(1)将杆件关键系数引入应力变化率法得到了一种改进的应力变化率法,即继承了传统应力变化率法判断杆件稳定性的优点,又体现了局部失稳发生前相邻结构杆件协同工作效果,解决了传统应力变化率法在结构发生变形失稳前应力变化率变化不显著的问题,通过关键系数K客观、量化地判断杆件移除顺序和预测结构失效模式,是分析结构鲁棒性的有效工具。为结构抗连续倒塌设计提供了技术手段。
(2)在静力阶跃荷载和竖向地震作用下,单层星型穹顶结构的失效模式为局部失稳造成的跨中节点位移突变,杆件内力从压力变为拉力,结构发生大变形失稳后在新的平衡位置平衡、振动,采用改进应力变化率法能在结构发生位移突变前进行有效预测。
(3)结构鲁棒性分析表明,当单根下弦索或单根撑杆发生破坏时,新型张弦桁架结构的敏感性系数小于1,表明结构不会因此立即发生倒塌,证明了高冗余度张弦桁架结构相对于传统张弦桁架结构具有较高的抗连续倒塌能力。
(4)新型张弦桁架结构改变了下弦索的数量和布置形式,使得建筑净空增加、拉索内力下降、上弦桁架跨中位置杆件拉应力增大,在设计中应适当增加跨中位置安全储备,在断索工况下该位置将出现塑性铰,从而延缓连续倒塌的发生、增强结构鲁棒性。
[1]张成,吴慧,高博青,等.非概率不确定性结构的鲁棒性分析[J].计算力学学报,2013,30(1):51-56.ZHANG Cheng,WU Hui,GAO Bo-qing,et al.Analysis of structural robustness with non-probabilistic uncertainties[J].Journal of Computational Mechanics,2013,30(1):51-56.
[2]蔡建国,王蜂岚,冯健,等.连续倒塌分析中结构重要构件的研究现状[J].工业建筑,2011,41(10):85-89.CAIJian-guo,WANG Feng-luan,FENG Jian,et al.Review of the key element for progressive collapse of structures[J].Journal of Industry Architecture,2011,41(10):85-89.
[3]蔡建国,王蜂岚,冯健,等.新广州站索拱结构屋盖体系连续倒塌分析[J].建筑结构学报,2010,31(7):103-109.CAI Jian-guo, WANG Feng-luan, FENG Jian, et al.Progressive collapse analysis of cable-arch structures of new Guangzhou railway station[J]. Journal of Building Structures,2010,31(7):103-109.
[4]蔡建国,王蜂岚,冯健.大跨空间结构抗连续性倒塌概念设计[J].建筑结构学报,2010,s1:283-287.CAI Jian-guo, WANG Feng-luan, FENG Jian. Concept design of progressive collapse for long-span space structures[J].Journalof Building Structures,2010,(sl):283-287.
[5]赵楠,马凯,李婷,等.防连续倒塌设计在张弦结构中的应用[J].钢结构,2011,26(5):38-44.ZHAO Nan, MA,Kai,LI Ting,et al. Application of preventing progressive collapse in beam string structure[J].Steel Structures,2011,26(5):38-44.
[6]周健,陈素文,苏骏,等.虹桥综合交通枢纽结构连续倒塌分析研究[J].建筑结构学报,2010,31(5):174-180.ZHOU Jian,CHEN Su-wen,SU Jun,et al.Progressive collapse analysis of a building in Hongqiao communication junction[J].Journal of Building Structures,2010,31(5):174-180.
[7]吕大刚,崔双双,李雁军,等.基于备用荷载路径Pushover方法的结构连续性倒塌鲁棒性分析[J].建筑结构学报,2009,(s2):112-118.LU Da-gang, CUI Shuang-shuang, LI Yan-jun, et al.Robustness analysis for progressive collapse of structures using ALP-based Pushover analysis approach[J].Journal of Building Structures,2010,(s2):112-118.
[8]丁阳,葛金刚,李忠献.空间网格结构连续倒塌分析的瞬时移除构件法[J].天津大学学报,2011,44(6):471-476.DING Yang, GE Jin-gang, LI Zhong-xian. Instaneous component-removing method for analysis of progressive collapse of space grid structure[J].Journal of Tianjin University,2011,44(6):471-476.
[9]王磊,陈以一.连续倒塌动力效应对极限承载力影响的数值分析[J].结构工程师,2009,25(4):30-34.WANG Lei,CHEN Yi-yi.Numerical analysis of the influence of dynamic effect in progressive collapse on ultimate bearing capacity[J].Structural Engineers,2009,25(4):30-34.
[10]郑阳,邹道勤,杨涛.基于悬链线理论的钢结构抗连续性倒塌分析[J].钢结构,2012,27(9):11-15.ZHENG Yang,ZOU Dao-qin,YANG Tao.Analysis of resist progressive collapse for steel structure based on the theory of catenary action[J].Steel Structures,2012,27(9):11-15.
[11]杜文风,高博青,董石麟,等.一种判定杆系结构动力稳定的新方法—应力变化率法[J],浙江大学学报(工学版),2006,40(3):506-510.DU Wen-feng,GAO Bo-qing,DONG Shi-lin,et al.New judgmentmethod on dynamic instability of truss structures:stress rate method[J].Journal of Zhejiang University(Engineering Science),2006,40(3):506-510.
[12]李志安,何江飞,高博青.大跨度张弦梁结构易损性及评估分析[J].建筑结构,2013,43(2):41-44.LI Zhi-an,HE Jiang-fei,GAO Bo-qing.Fragility analysis and assessment of large-span beam string-structures[J].Building Structures,2013,43(2):41-44.
[13]何江飞,高博青.桁架结构的易损性评价及破坏场景识别研究[J].浙江大学学报(工学版),2012,46(9):1634-1637.HE Jiang-fei,GAO Bo-qing.Vulnerability assessment and failure scenarios identification of truss structures[J].Journal of Zhejiang University(Engineering Science),2012,46(9):1634-1637.
[14] Liu Guoguang,Wu Zhiwei,Cai Jing.Study on static and dynamic behaviors of truss string structure with double cables,The seventh international conference on advances in steel structure[C],2012:900-907.
[15]杜文风,高博青,董石麟.改进悬臂型张弦梁结构理论分析及试验研究[J].建筑结构学报,2010,31(11):57-64.DU Wen-feng,GAO Bo-qing,DONG Shi-lin.Theoretical and experimental study of an improved cantilever string structure[J].Journal of Building Structures,2010,31(11):57-64.
[16]刘国光,武志玮.具有荷载缓和功能的双索张弦桁架结构静动力性能研究[J].空间结构,2013,19(3):82-87.LIU Guo-guang,WU Zhi-wei.Research of static and dynamic performances on truss string structure with double cableswith load relieving function[J].Spatial Structures,2013,19(3):82-87.
[17]刘国光,武志玮,谭振.一种高冗余度张弦桁架结构及实施方法[P].中国:CN 201210138384.4,2012.

