试件弹塑性阶段的地震模拟台控制方法研究
田 磐, 陈章位
(1.浙江大学 流体动力与机电系统国家重点实验室,杭州 310027;2.镇江高等专科学校 机械系,江苏 镇江 212003)
地震模拟台试验可在土木工程领域验证建筑物的抗震性能,该试验能够在实验室环境下比较直接和精确的模拟出实际地震的工况[1]。
为实现较高的试验精度,文献[2-3]采用加速度迭代控制方法,而文献[4]采用位移迭代控制方法,分别对系统的加速度阻抗或位移阻抗进行辨识,上述文献通过理论和试验研究表明,该类方法在试件弹性阶段下能获得较好的试验效果。上述方法在试验过程中不断对系统进行辨识,以适应被控对象传递特性的变化,但是存在如下缺点:① 没有同时对加速度阻抗和位移阻抗进行辨识(低频段加速度阻抗辨识精度会下降,而中频段位移阻抗辨识精度会下降);② 更新周期是以单帧试验时间为单位的,系统辨识的速度较慢。而对于地震模拟试验,随着试验量级逐渐增大,试件由弹性状态进入弹塑性状态,试件动态特性会发生较快变化,系统辨识的速度会落后于系统特性改变的速度,从而对试验精度产生较大影响。目前相关国家标准《GB 50011-2010建筑抗震设计规范》[5]已经对试件的弹塑性分析提出了要求。
针对出现的问题,本文通过仿真研究分析了地震模拟台在试件弹塑性阶段的传递特性变化;为适应试件动态特性发生较快变化,提出一种地震模拟快速迭代控制方法,实现了频域范围内的分段辨识,针对变化较快的中频段(通常为2-80 Hz)系统传递特性,采用短时间加速度控制信号进行辨识,提高辨识的更新速率;而对于特性变化较慢的低频段(通常为0.1-2 Hz)系统传递特性,采用长时间位移控制信号进行辨识,以满足地震模拟试验的下限频率。最后,在浙江大学构建的地震模拟台上,通过试验验证了该控制方法在试件弹性阶段和弹塑性阶段都能得到较好的控制效果。

表1 试件在不同试验阶段的仿真参数(输入量级1 g)Tab.1 Simulation parameters of specimen of different stage
1 地震台在试件弹塑性阶段的传递特性研究
1.1 试件弹塑性阶段中的特性变化
地震模拟试验多采用多次多级加载方案,随着试验量级逐渐增加,试件一般要经历弹性反应阶段(试验量级较小)和弹塑性反应阶段(随着试验量级增大,结构出现裂缝,损坏逐渐严重),叶献国等[6-7]通过理论和试验研究总结出,试件进入弹塑性阶段后,试件的固有频率和阻尼比会出现较大变化。文献[6]通过理论分析和试验验证表明,对某钢筋混凝土框架结构缩尺模型进行地震模拟试验,随着试验量级的增加,试件进入弹塑性阶段而出现开裂以及损坏现象时,其试件动态特性会发生变化,前几阶试件固有频率会下降,而阻尼比会出现增大,且一阶固有频率下降最大,不同试验量级下试件n阶固有频率fn与试件初始固有频率fn0比值如图1所示:
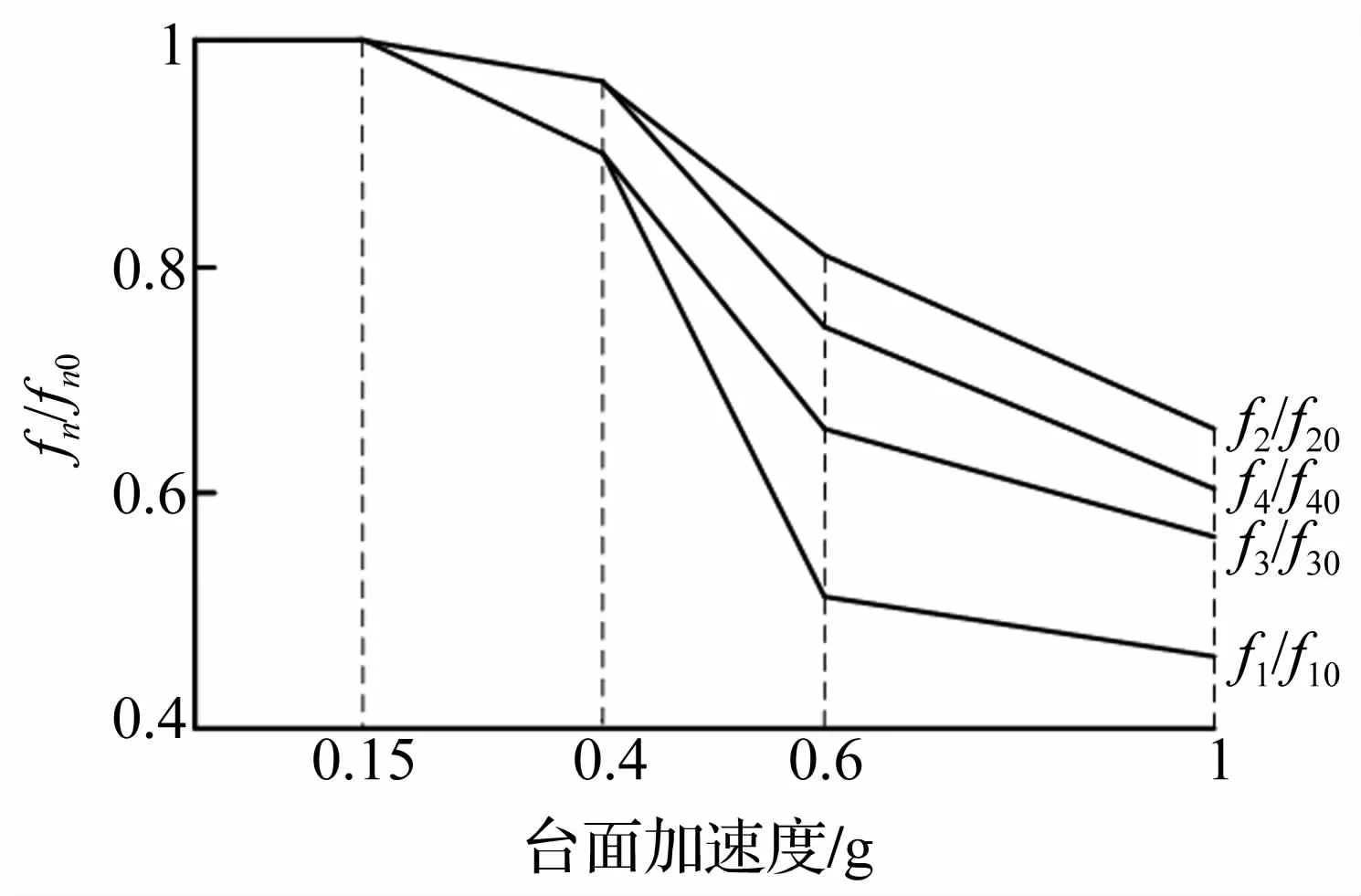
图1 不同输入量级下弹塑性阶段试件固有频率的变化Fig.1 Natural frequency changes of elastoplastic specimen under different inputmagnitude
1.2 地震模拟台系统传递特性仿真研究
试件特性的变化会导致地震模拟台系统传递特性的变化,故通过仿真对系统传递特性进行研究。利用典型小型地震模拟振动台作为仿真地震模拟平台,参数如下:振动台最大推力为40 kN,最大位移±130mm,最大速度0.5 m/s,满载时最大加速度2 g,频率范围为0.5-20 Hz,台面质量为500 kg。
建立500 kg试件模型,试件前两阶固有频率在试验频率范围内,模拟试件在弹塑性阶段的动态特性变化,参照图1中的输入量级为1 g的试验数据建立试件在弹性阶段和弹塑性阶段的参数如表1所示。
利用振动台和试件参数组成地震模拟仿真试验对象,利用文献[8]中介绍的三参量伺服控制方法对系统进行校正后,得到弹塑性阶段前后的系统加速度传递特性,如图2所示:
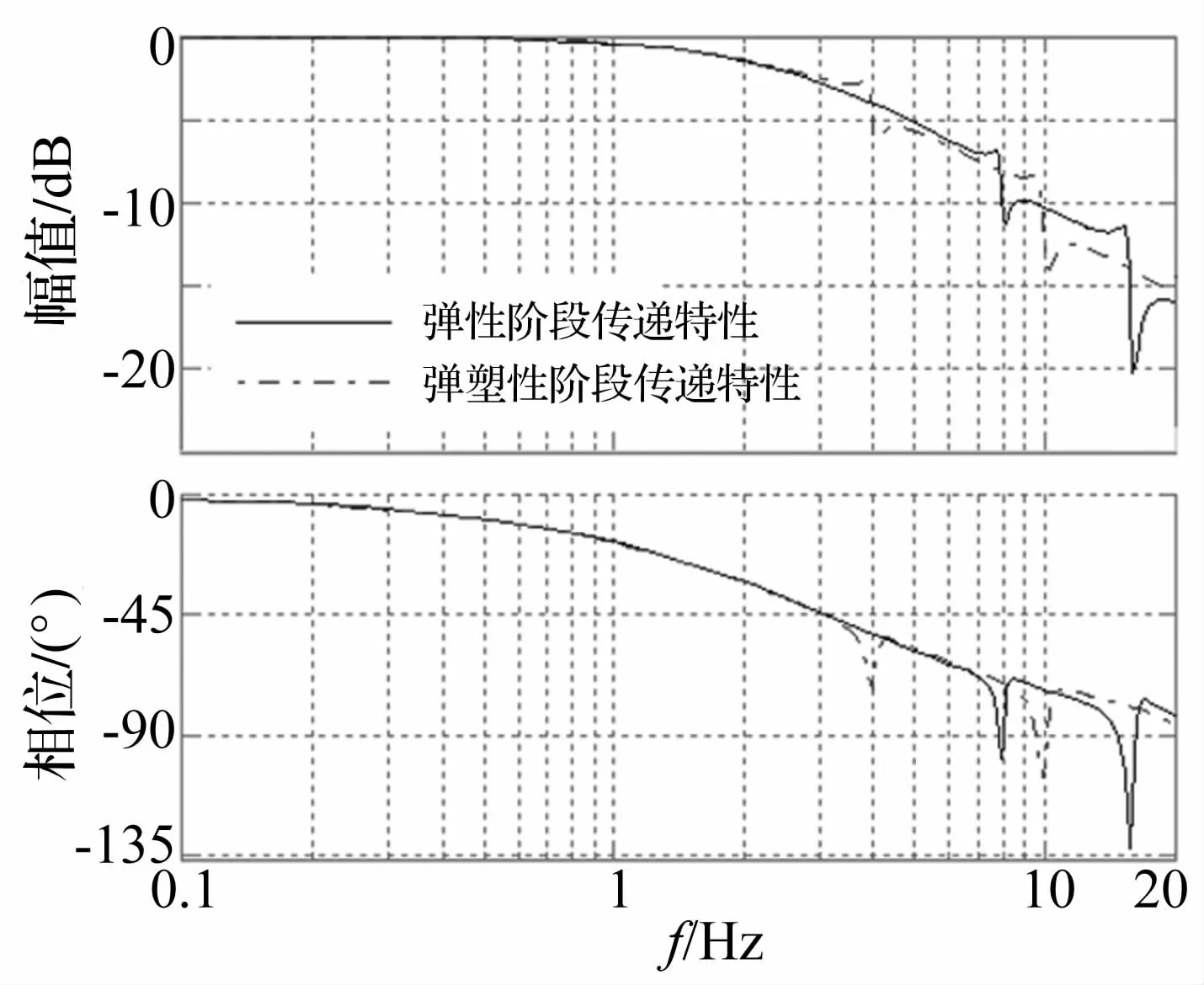
图2 弹塑性阶段前后的系统加速度传递特性Fig.2 Frequency response of shaking table before and after elastoplastic stage
从仿真结果来看,试件进入弹塑性阶段后的系统加速度传递特性出现一定的变化,变化规律如下:
(1)在试件1/2倍一阶固有频率范围内(低于2 Hz范围内),系统动态特性变化很小;
(2)在试件1/2倍一阶固有频率范围外,系统动态特性发生一定的变化,特别在试件的固有频率处,系统的加速度幅频特性和相频特性发生了较大的变化。
2 加速度迭代控制方法分析
加速度迭代控制不断对振动台系统传递特性进行辨识,进而对驱动信号进行补偿,以获得较好的地震模拟试验精度,其控制原理如图3所示。
2.1 控制原理
(1)预试验步骤:使用小量级白噪声信号作为驱动信号输入振动台系统,由驱动信号和相应的加速度控制信号估计系统加速度阻抗,再通过系统加速度阻抗和加速度参考信号获得系统的驱动信号,输入振动台开始首帧地震模拟试验;

图3 加速度迭代控制方法示意图Fig.3 Schematic diagram of acceleration iterative control
(2)迭代更新:测量在首帧驱动信号作用下的振动台加速度控制信号,利用新的驱动信号和加速度控制信号进行系统辨识并更新系统加速度阻抗,生成新一帧的驱动信号并实现驱动信号的平滑连接[9]。重复该步骤,不断更新驱动信号,并进行驱动信号之间的平滑连接,直到试验结束。
2.2 存在的不足
加速度迭代控制是以帧作为系统辨识更新周期的,通常一帧地震模拟时间在20秒以上,当试件传递特性迅速变化时(进入弹塑性阶段后),该控制方法的系统辨识会有明显的滞后。
将系统辨识的更新周期缩短,理论上能提高系统辨识的快速性。但是地震模拟试验下限频率很低(核电设备地震模拟试验下限频率可达到0.1 Hz以下[10]),根据数字信号处理理论,如果系统传递特性下限频率为0.1 Hz以下,则系统辨识所需时域信号长度在10秒钟以上[11],从而限制辨识快速性的提高。
3 地震模拟快速迭代控制方法
针对传统控制方法在试件弹塑性阶段下存在系统辨识滞后的缺陷,本文提出一种地震模拟快速迭代控制方法,在实现较高系统辨识分辨率的基础上提高系统辨识更新速度,与传统地震模拟控制方法相比,该控制方法的特点为:
(1)采用频域分段的方法利用位移和加速度控制信号分别对低频段和中频段系统阻抗进行辨识,设置不同的辨识参数,使得低频段系统阻抗具有较高的频率分辨率,而中频段系统阻抗具有较高的更新速率;
(2)设计驱动信号合成算法,使得系统总驱动信号由低频段系统阻抗和中频段系统阻抗合成生成。
3.1 系统传递特性的分段辨识
3.1.1 低频段系统阻抗辨识
在低频段,位移传感器输出精度要高于加速度传感器输出精度[4],所以低频段的系统传递特性是基于位移阻抗而生成;由上文可知在各个试验阶段系统低频段传递特性变化较小,故采用长时间时程数据(整帧地震模拟信号)对系统位移阻抗进行估计,能够满足低频段的系统时变性的要求;同时采用长时间数据进行系统辨识能实现较高的频率分辨率,满足系统下限频率的需要。
位移阻抗辨识方法采用基于输出误差模型的阻抗估计方法,即H1法:

式中:Si为驱动信号的自功率谱,Sdio为驱动信号和位移传感器输出信号的互功率谱位移阻抗以整帧地震模拟时间T作为辨识周期,当采样频率为f时,试验数据点数N=T×f,频率分辨率Δf=1/T。通常地震模拟整帧信号T大于20 s,即频率分辨率小于0.05 Hz,能满足地震模拟试验下限频率的要求。
利用低通滤波环节 GL(f)对位移阻抗 Zd(f)进行处理后,可得低频段系统阻抗:
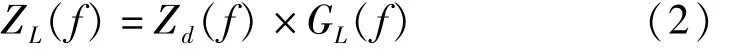
3.1.2 中频段系统阻抗辨识
在中频段,加速度传感器输出精度要高于位移传感器输出精度,所以中频段的系统传递特性是基于加速度阻抗而生成;考虑到弹塑性阶段中频段系统阻抗变化较快,故采用短时间时程数据(对整帧地震模拟信号进行分块)进行加速度阻抗估计,以实现较快的系统辨识更新速率。加速度阻抗估计方法如下:

式中:Si为驱动信号的自功率谱,Saio为驱动信号和加速度传感器输出信号的互功率谱。地震模拟试验整帧时间为T,当采样频率为f时,试验数据点数为N=T×f。将试验时程平均分割为m块,加速度阻抗以块数据时程长度T/m作为辨识周期,块数据的试验数据点数为N=T×f/m,频率分辨率Δf=m/T。与使用整帧数据辨识相比,进行分块辨识能够使得加速度阻抗更新速度加快m倍;加速度阻抗的下限频率(即频率分辨率f)也增加了m倍,为实现频率匹配,中频段的下限频率应高于加速度阻抗的频率分辨率。
利用高通滤波环节GM(f)对加速度阻抗进行处理后,可得中频段系统阻抗:

3.1.3 滤波环节的设计
设计滤波环节 GL(f)和 GM(f),使得低频段系统阻抗主要由位移阻抗构成;而中频段系统阻抗主要由加速度阻抗构成,滤波环节公式如下:
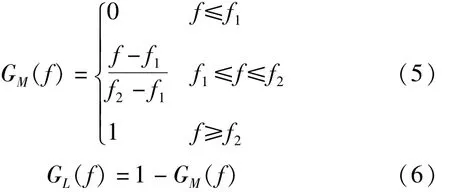
由于GM(f)+GL(f)=1,故滤波环节不会影响系统的动态特性。
式(5)中的f1和f2值决定着低频段和中频段的范围,低于f2的频率范围为低频段,高于f1的频率范围为中频段,为实现平滑过渡,两者有重叠区域。频率区域设置原则为:
(1)考虑到弹塑性阶段试件低阶固有频率处动态特性变化较快,应使得试件的低阶固有频率高于低频段频率范围,以实现对该频率段系统传递特性的快速辨识;
(2)为保证较高的系统辨识精度,位移传感器在低频段内应具有较为平坦的幅频特性,即f2要低于位移传感器0.5 dB上截止频率;而加速度传感器在中频段内应具有较为平坦的幅频特性,即f1要高于加速度传感器0.5 dB下截止频率。
3.1.4 驱动信号的合成生成
由文献[12]可知,对于地震模拟试验,无论采用加速度时域复现方式还是位移时域复现方式,其系统驱动信号相同,即:

式中:Ra(f)和 Rd(f)为加速度和位移参考信号的复频谱,Za(f)和 Zd(f)为估计出的系统加速度和位移阻抗。由式(2)、(4)、(7)求得系统驱动信号复频谱:

将式(8)进行傅里叶逆变换可得到系统时域驱动信号:

系统时域驱动信号由低频段驱动分量dL(t)(式右端第一项)和中频段驱动分量dM(t)(式右端第二项)组成,两者需实现同步输出。
因为dM(t)由更新较快的中频段系统阻抗生成,故只能直接得到中频段驱动分量片段,为得到整帧时域驱动信号,需采用重叠相加技术[13]对驱动分量片段进行连接,假设单帧地震模拟试验数据点数为512(含128点补零数据点数),当加速度阻抗辨识分块数m=4时(即加速度阻抗辨识周期为128数据点),其算法原理如图4所示:
(1)将单帧加速度参考信号ra(t)分为m-1=3块;
(2)将第n块加速度参考信号ran(t)与不断更新的中频段系统阻抗ZM(f)的逆(即滤波器序列hn(t)=IF-FT(ZM(f)))进行卷积生成中频段驱动分量片段 dn(t)=ran(t)×hn(t);
(3)将中频段驱动信号片段进行连接生成中频段驱动分量 dM(t)。
4 试验研究
利用浙江大学构建的地震模拟台进行试验研究,如图5所示,振动台推力为20 kN,最大位移±125 mm,最大速度1 m/s,满载最大加速度2 g。试验采用浙江大学和杭州亿恒公司开发的振动控制平台,在该控制器平台上实现加速度迭代控制和地震模拟快速迭代控制方法。

图4 重叠相加技术原理图Fig.4 Schematic diagram of overlap technology

图5 浙江大学水平式地震模拟台Fig.5 Horizontal shaking table of Zhejiang university
为验证本文讨论控制算法的有效性,设计两个4层钢框架结构试件,分别用来模拟实际试件弹塑性阶段前后的动力学特性(进入弹塑性阶段后,试件的固有频率下降而阻尼比增大),两个试件除楼板间连接钢片厚度不同外,其他结构完全相同。如图6所示,试件长边为350 mm,短边为250 mm,结构层高为207 mm,楼板高度40 mm,楼板间连接钢片厚度分别为4.5 mm(试件1)和2 mm(试件2),宽度为29 mm,楼板质量为17 kg,楼板和钢片采用螺栓连接,可近似为固定连接。试件为钢制材料,弹性模量E=2.0×1011Pa,密度ρ=7.8×103kg/m3,解析计算得出的试件低阶固有频率理论值如表2所示。
试验采用El-Centro地震波(时域未压缩),参考信号进行滤波后频宽为0.25~20 Hz,峰值加速度0.29 g,峰值位移为48.9mm,数据两端补零点后每帧长度为43.67 s。
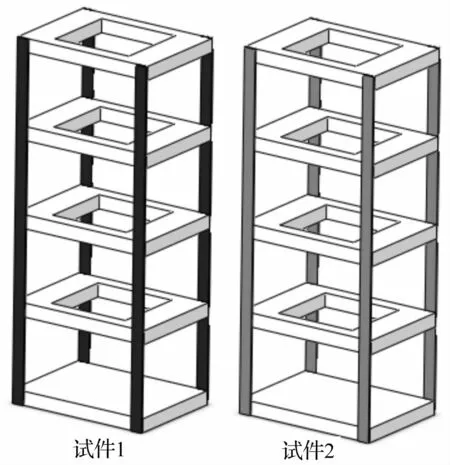
图6 地震模拟试验试件Fig.6 Specimens for earthquake simulation test

表2 试件的理论固有频率值Tab.2 Theoretical natural frequency of specimens
该地震模拟台采用MESSOTRON公司DLH型LVDT位移传感器和中国地震局力学所的941B加速度传感器。由相关技术手册可知,位移传感器在2 Hz处幅频特性下降小于0.5 dB;而加速度传感器在1 Hz处幅频特性下降小于0.5 dB。根据上文中对滤波环节参数的设置原则,确定f1和f2为1 Hz和2 Hz。
为克服非线性以及系统噪声的影响,控制策略必须要对系统阻抗进行平均化处理[14],在本试验中,两种控制策略辨识出的系统阻抗均经过相同的指数平均化处理,原理如下:
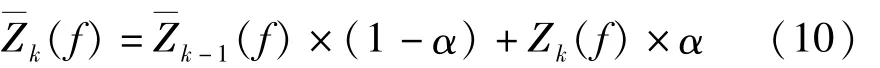
式中k(f)为第 k次平均值,Zk(f)第 k次新记录,α=0.25为加权系数。
首先使用加速度迭代控制方法进行五帧地震模拟试验,利用整帧数据对加速度阻抗进行辨识:辨识周期为 43.69 s,采样频率为 46.875 Hz,数据点数为 2 048,频率分辨率为0.022 9 Hz。对试件1进行地震模拟试验,三帧迭代修正后,生成的加速度控制信号如图7所示,为方便观测,加速度信号截取其中5秒钟的信号数据。
从控制信号和参考信号比较来看,其相关系数为92%(如图7所示),为模拟试件进入弹塑性阶段,保存此时的系统加速度阻抗(如图8所示)。

图7 加速度迭代控制方法试验第三帧的时域波形图Fig.7 Third frame waveform of acceleration iterative control

图8 加速度迭代控制辨识出的系统加速度阻抗(第三帧)Fig.8 The system acceleration impedance identified by acceleration iterative control(the third frame)
将试件1更换为试件2,利用保存的加速度阻抗直接生成驱动信号输入振动台继续进行试验,该步骤可较为真实的模拟出实际试件在弹塑性阶段的特性突然变化;对试件2进行两帧地震模拟试验,对驱动信号进行迭代修正,生成的第四帧和第五帧加速度控制信号如图9和10所示(截取5秒钟信号)。其控制信号和参考信号的相关系数分别为68%,79%。
上述数据表明该方法在试件特性发生突然变化后,试验控制精度出现较大下降,但由于系统辨识更新速率较慢,导致时域相关系数较低。

图9 加速度迭代控制方法试验第四帧的时域波形图Fig.9 Fourth frame waveform of acceleration iterative control

图10 加速度迭代控制方法试验第五帧的时域波形图Fig.10 Fifth frame waveform of acceleration iterative control

图11 快速迭代控制方法试验第三帧的波形图Fig.11 Third frame waveformof rapid iterative control
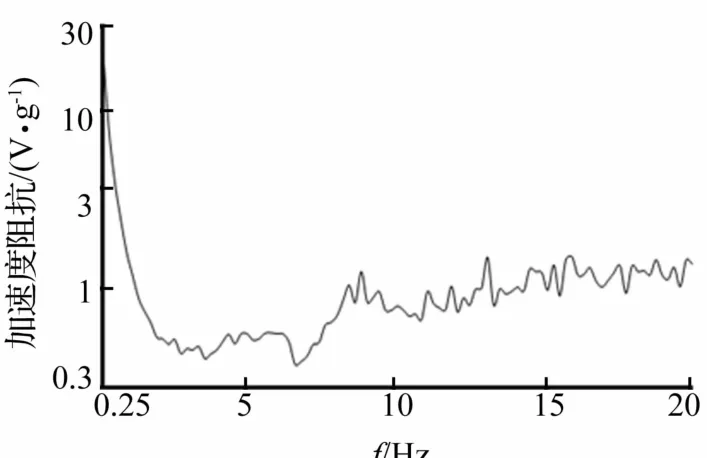
图12 快速迭代控制辨识出的系统加速度阻抗(第三帧)Fig.12 The system acceleration impedance identified by rapid iterative control(the third frame)

图13 快速迭代控制辨识出的系统位移阻抗(第三帧)Fig.13 The system displacement impedance identified by rapid iterative control(the third frame)
然后利用本文介绍的快速迭代控制方法进行五帧地震模拟试验,利用整帧数据对位移阻抗进行辨识:辨识周期为 43.69 s,采样频率为 46.875 Hz,数据点数为2 048,频率分辨率为0.022 9 Hz;将整帧数据均分为8块对加速度阻抗进行辨识:辨识周期为5.46 s,采样频率为46.875 Hz,每块的数据点数为256,频率分辨率为0.182 4 Hz。对试件1进行地震模拟试验,三帧迭代修正后,生成的加速度控制信号(截取5秒钟信号)如图11所示,其参考信号和控制信号相关系数能达到93%。
分别保存辨识出的位移和加速度阻抗(如图12和13所示),更换试件2后,利用保存的系统阻抗生成驱动信号进行地震模拟试验,模拟弹塑性阶段试件传递特性的变化,连续对驱动信号进行两帧迭代修正,生成的加速度控制信号如图14和15所示(截取5秒钟信号),其控制信号和参考信号的相关系数分别为74%,90%。五帧试验后辨识出的的系统加速度阻抗如图16所示。

图14 快速迭代控制方法试验第四帧的波形图Fig.14 Fourth frame waveform of rapid iterative control
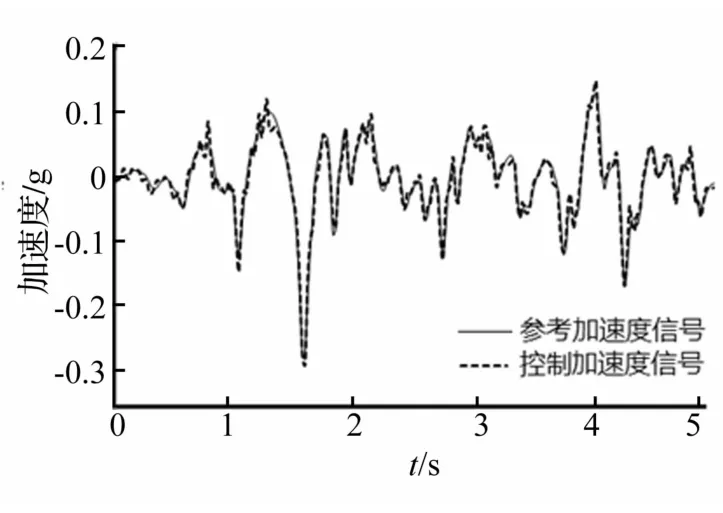
图15 快速迭代控制方法试验第五帧的波形图Fig.15 Firth frame waveform of rapid iterative control
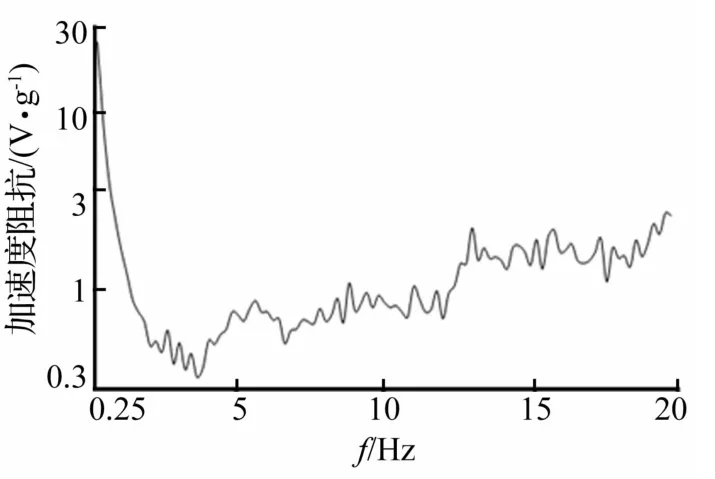
图16 快速迭代控制辨识出的系统加速度阻抗(第五帧)Fig.16 The system acceleration impedance identified by rapid iterative control(the fifth frame)
从试验结果来看,两种控制方法在试件动态特性变化较小的工况下(弹性阶段),控制精度均较高。当试件特性发生突变后(进入弹塑性阶段),虽然两种控制方法的控制精度都出现了较大下降,但是快速迭代控制方法的辨识速率是加速度迭代控制方法的8倍,故能较快的更新系统传递特性,快速提高地震模拟时域复现精度,有效的克服了传统加速度迭代控制系统辨识速度较慢的缺点。
5 结 论
本文针对试件弹塑性特性导致地震模拟试验精度下降,提出一种地震模拟快速迭代控制方法,和传统的加速度迭代控制进行比较。通过理论和试验研究,得到下列结论:
(1)通常地震模拟试验下限频率较低,而在试件进入弹塑性阶段后,系统的传递特性变化较快,采用频域分段辨识方法,不仅能保证低频段具有较高的系统辨识分辨率,同时在中频段实现了较快的系统辨识更新速率;
(2)在频域分段辨识方法的基础上,设计合成方法生成系统总驱动信号,在试件传递特性突然发生变化后,该方法能够在两帧试验时间内使得加速度波形复现时域相关系数能达到90%以上。
[1]王燕华,程文韍,陆飞,等.地震模拟振动台的发展[J].工程抗震与加固改造,2007,29(5):53-56.WANG Yan-hua,CHENG Wen-rang, LU Fei et al.Development of the shaking table[J].Earthquake Resistant Engineering and Retrofitting,2007,29(5):53-56.
[2]丛大成,何景峰,韩俊伟.地震模拟试验台数字控制系统研究[J].仪器仪表学报,2009,30(s6):480-484.CONG Da-cheng,HE Jing-feng,HAN Jun-wei.Study of digital control system for seismic simulation test rig[J].Chinese Journal of Scientific Instrument,2009,30(s6):480-484.
[3]Kuehn J,Epp D,PattenW N.High-fidelity control of a seismic shake table[J].Earthquake Engineering&Structural Dynamics,1999,28(11):1235-1254.
[4]严侠,牛宝良,宋琼.通过位移复现控制实现地震加速度波模拟[J].世界地震工程,2011,27(3):97-100.YAN Xia, NIU Bao-liang, SONG Qiong. Displacement waveform replication method for earthquake simulation[J].World Information Earthquake Engineering,2011,27(3):97-100.
[5]GB 50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2001.
[6]叶献国,徐勤,李康宁,等.地震中受损钢筋混凝土建筑弹塑性时程分析与振动台试验研究[J].土木工程学报,2003,36(12):20-25.YE Xian-guo,XU Qin,LI Kang-ning et al.Experimental research on inelastic time-history analysis and shaking table test for a reinforced concrete building damaged in earthquake[J].China Civil Engineering Journal,2003,36(12):20-25.
[7]汪梦甫,周锡元.高层建筑结构抗震弹塑性分析方法及抗震性能评估的研究[J].土木工程学报,2003,36(11):44-49.WANGMeng-fu,ZHOU Xi-yuan.Modified pushover analysis and seismic performance evaluation for tall building[J].China Civil Engineering Journal,2003,36(11):44-49.
[8]田磐,陈章位.基于弹性负载的地震模拟试验控制策略[J].振动与冲击,2013,32(5):26-30.TIAN Pan, CHEN Zhang-wei. A control strategy of earthquake simulation test based on elastic payload[J].Journal of Vibration and Shock 2013,32(5):26-30.
[9]于慧君,陈章位,王庆丰.一种加窗重叠信号平滑连接方法及其在振动信号预处理中的应用[J].振动与冲击,2007,26(8):39-40.YU Hui-jun, CHEN Zhang-wei, WANG Qing-feng. Ola signal smooth linking method and its application in vibration signal pre-processing[J].Journal of Vibration and Shock,2007,26(8):39-40.
[10]方重.大型模拟地震振动台主要参数的确定及技术经济分析[J].世界地震工程,2001,17(4):135-138.FANG Zhong.Determination of main parameters and technical-economic analysis for large scale earthquake simulator[J].World Information Earthquake Engineering,2001,17(4):135-138.
[11]胡广书.数字信号处理:理论,算法与实现[M].北京:清华大学出版社,2003.
[12]黄浩华.地震模拟振动台的设计与应用技术[M].北京:地震出版社,2008:153-160.
[13]Smith S W.Digital signal processing[M].SanDiego:California technical Publishing,1999.
[14]杭州亿恒科技有限公司.振动控制器,Super VT-系列[Z].

