推广的Stancu算子的A-统计逼近
刘生贵
(嘉应学院 数学学院,广东 梅州 514015)
0 引言
文献[1]中,Stancu D D 引入如下一类线性算子:
设0<αn,f∈C[0,1],

这里
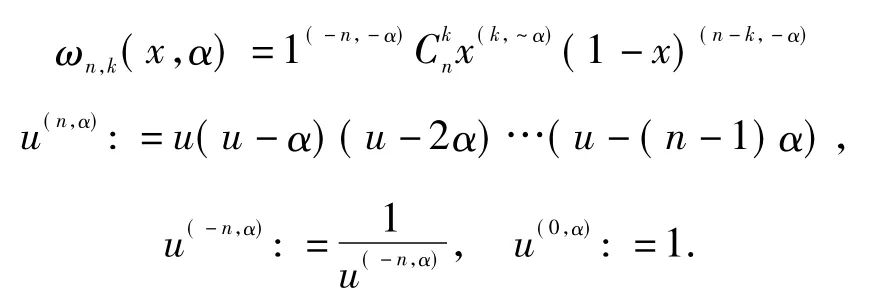
显然,当αn≡0 时,Stancu 算子即为熟知的Bernstein算子.Stancu 算子是非常重要的算子,它的逼近性质吸引了众多学者的研究和探索[2~3].
近年来,线性算子的统计逼近被逐步引入逼近论领域[4~7].把统计收敛的理念引入到逼近论领域大大促进了逼近论的发展,特别是Cesàro 型矩阵可求和方法有力弥补了各类线性算子(例如Hermite-Feiér 插直算子)收敛性质上的不足,因为这些算子在那些简单的不连续点上并不收敛[8~9].A-统计收敛正线性算子的求和上显得更为有效[5~7].
设{xn}n∈N是一个数字序列,如果对任给ε>0,有
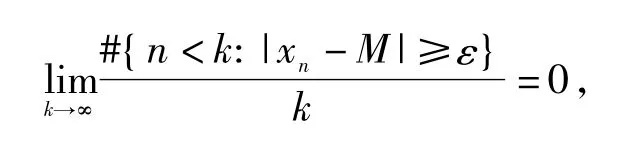
则称{xn}n∈N统计收敛于数M,这里#B 表示集合B的基数[10~11].{xn}n∈N统计收敛于数M,记为

设A=(ajn)是一个无限的可求和矩阵,记x=(xn),如果对每一个收敛,则记关于x=(xn)的变换为Ax:=(Ax)j.我们说矩阵A 正则的,如果当limj→∞xj=M 时,有limj→∞(Ax)j=M[12].例如,定义如下的Cesàro 矩阵C1=(cjn)

就是一个正则矩阵,设A 是非负可求的正则矩阵,Freedman 和Sember[13]引入了A-统计收敛.它是一种更为一般方法的统计收敛.我们说序列(xn)n∈NA-统计收敛到M,如果满足对任给ε>0,式子
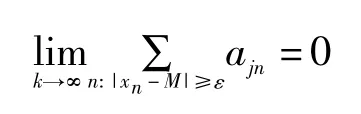
成立.A-统计收敛到M,记为
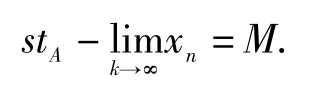
若将A 用单位矩阵代替,则A-统计收敛就是普通意义的收敛,不难看出,如果取A=C1,则C1统计收敛就是上面所提到的统计收敛,即

对任给的非负的正则矩阵,每一个收敛列A 统计收敛于同一的值,但它的逆命题不成立.特别,Kolk[14]已经证得,当非负正则矩阵A=(ajn)满足条件limnmax{ain}=0 时,A-统计收敛强于普通意义的收敛.
本文定义一类推广的Stancu 算子如下:设0≤αn,f∈C[0,1],

这里

本文将研究该算子A—统计逼近的性质,同时,借助光滑模,讨论A—统计逼近收敛速度的估计.
1 算子的A-统计逼近
先给出主要结果所需的两个引理.
引理1设n∈N 和0≤αn,f∈C[0,1],有

这里ei=tifor i=0,1,2.
证明
由Vandermode 公式

得

引理2[15]设A=(ajn)是一个非负正则可求和矩阵,若从C[a,b]到C[a,b]线性算子序列Ln满足
这里ei=ti,i=0,1,2.则对任意f∈C(a,b),有
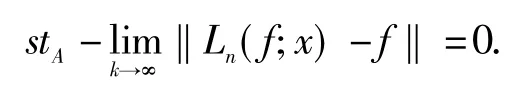
定理1设A=(ajn)是一个非负的正则可求和矩阵,序列{αn}满足

则对所有的f∈C[0,1],有

证明由式(1),(2),(3),显然有

对给定的ε>0,定义如下集合:
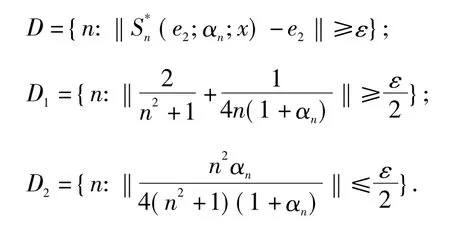
由(3)式可知D⊆D1∪D2.对每一个j∈N,有

在(8)式中让j→∞并应用(4)式可得
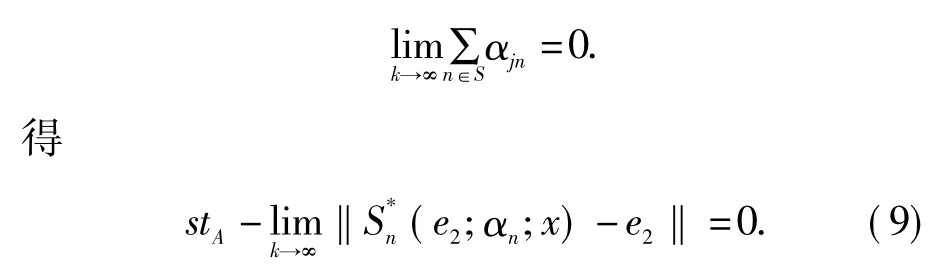
由引理2,并应用(5),(6),(9)式,可得定理结果.
2 A-统计逼近的收敛速度估计
我们将借助光滑模,计算算子A-统计收敛的收敛速度.
对于连续函数f,函数f 的光滑模ω(f,δ)定义为

又知,对于光滑模有limδ→0ω(f,δ)=0,由光滑模的性质,有
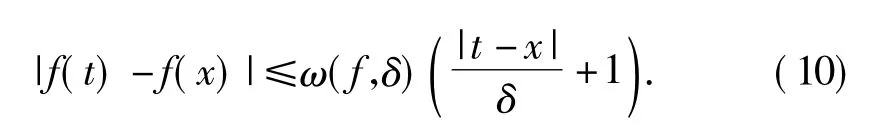
定理2设n∈N,f∈C[0,1],{αn}是满足0<αn的序列,则

证明由于算子是正线性算子,所以有

由(10)式,对任意δ>0,有


由正线性算子的Canchv-Schwarz 不等式,可得

上式中取即可得定理结果.

