三角模糊环境下城市出租车合乘需求预测
王保玲,黄承锋,蒋 思
(1.重庆交通大学 管理学院,重庆 400074;2.重庆交通大学 财经学院,重庆 400074)
0 前言
近年来,“打车难”和出租车“拒载”等问题在城市居民的日常出行中经常遇到.为解决类似的问题,目前可行的有两个方法:第一个方法是增加出租车的数量,第二个方法是提高出租车利用率.从我国实际出发,我国城市交通基础设施建设不是很完善,无法满足日益增长的城市汽车保有量增长速度;从社会环境出发,汽车尾气等温室气体排放所带来的全球气候变暖和温室效应,已经使各地环境问题频频发生;从国家政策出发,“低碳交通”和“低碳出行”也已成为可持续发展理念下国家的必要之举.因此,为了减少交通拥堵和改善城市环境,提高出租车的利用率,倡导出租车合乘方式相对于增加出租车数量是更为有效的途径.
Kwon 等人[1]基于HOV 车道研究利用合理费税设置等经济措施发展拼车出行方式.国内对于出租车合乘的研究主要集中在制度和运营模式这两个方面.张有恒(1997)[2]在文中详细的描述了车辆合乘的定义与实施的环境背景、车辆合乘的成本效益评估与需求预测模式以及实施车辆合乘的成功要件与行销策略的建立.覃运梅(2006)在《出租车合乘模式的探讨》[3]中提出了租车合乘的几种运营模式,考量司机、乘客双方利益,建立了相应的数学模型及乘客合乘查询系统,并得出了最佳行驶路线和合理费用.卢川,吴群在《城市居民出行合乘出租车问题的研究》[4]中讨论了合乘的类型划分和合乘车辆数的确定等问题。
出租车合乘是由实际需求量、保有量、政府补给量三者组成,通过横向链接组成链状或网络结构,它们的关系本质上表现为供给和需求的关系.在出租车客运的实际运作过程中,需求量在时间上存在明显的差异性和模糊性,合乘的具体操作模式也存在不确定性.本文基于可信性理论和统计学,预测出合乘的需求量,为加强出租车市场的管理和城市居民的出行导向提供一定的科学和技术支撑.
1 三角模糊环境下乘车需求
针对不确定性或信息偏好,学术界广泛使用模糊集理论来表述.特别是在缺乏确定性数据或较为完整的可用历史数据的条件时,模糊集理论可以比较好地屏蔽数据的缺陷,预测出评估值.这种方法对处理不确定的出租车需求量提供了一个选择和方便的框架.三角模糊数TRFN(Triangular Fuzzy Number)是一类利用模糊集来解决不确定性环境下决策问题的特殊模糊数,被广泛应用于风险管理、绩效评价和模糊规划等.本文拟用三角模糊数描述出租车供应链节点乘客面临的市场需求.
1.1 三角模糊数
本文拟用三角模糊数变量ξ=(a,m,b)描述出租车面临的市场需求.ξ=(a,m,b)表示的含义为“出租车客运的市场需求取值范围介于a 和b 之间,最可能取值为m”.三角模糊需求的隶属函数如图1 所示:

1.2 模糊环境下城市乘车需求
城市出租车的合乘现象大部分出现在如上、下班高峰、节假日等具有明显高峰出行需求的时间段.在这个时段,途中的出租车基本供需满载,市民打车相对困难,且地点主要集中于城市主城区,如大型商业圈、火车站等人口密集的区域.根据城市居民的日常出行情况,将一天划分为n 个合乘期,各个合乘期内的出租车需求是相互独立的.对模糊变量中最可能取值的大小进行排序,从而得到不同合乘期的三角模糊变量.由隶属度的定义可知最大可能需求量对应的隶属度等于1.经过排序后的隶属度函数见图2:
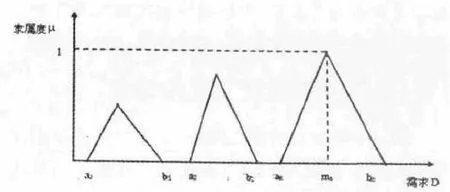
对三角模糊隶属度函数进行排序的目的是要找出城市居民日常出行中乘车最紧张的时段及出相应的租车需求量,这是因为市民出行高峰期,出租车供应最紧张的乘车时段是产生出租车合乘需求最多的时段.根据三角模糊数变量的隶属函数定义、估计变量取值范围和需求最可能的值,建立模糊环境和“一乘客一车”模式下城市出租车车辆需求的模型为:

2 合乘模式下的出租车合乘需求预测
“合乘”是指在客运高峰时段或路段,乘客经协商同意共同乘坐同一辆出租车,这是一种自愿行为、合法行为.“拼客”是指出租车司机为了追求更高的利益而多载客人,这种行为侵害了乘客的权益,是违规的.“合乘”和“拼客”是完全不同的法律行为.由合乘的概念可知,只有在出租车供不应求的情况下才会产生合乘需求,其需求量就是出租车客运实际需求量与保有量之间的供应缺口.根据“一乘客一车”的等比例关系式,由出租车实际需求量所能满足的人口数推算出客运缺口所能满足的人数,结合合乘模式下的概率因子,确定合乘车辆数占保有量的比例,进而预测出合乘的需求量.
2.1 “一乘客一车”模式下的供应缺口
假设一两出租车每次只搭乘一位乘客,地区出租车乘客量为P,地区总人口数为Z,现有的乘客量P 占该地区总人口Z 的比例为常数a(则P=a·Z),出租车现有保有量Q'和政府每年增加的供给量S(车辆供给呈均匀分布).
1)本年份出租车保有量Q.政府增加出租车车辆的供给成均匀分布,将分布函数的数学期望作为政府增加的出租车量,则有

2)出租车客运的供应缺口出租车量V.乘客对出租车的需求量与客运公司提供的出租车车辆数之间存在不均衡造成合乘需求,供应缺口就是供给与需求之间的差值,即

3)出租车供应缺口下乘不到出租车的人数为P'.根据一辆车只承载一乘客的等比例关系式,出租车需求量与城市乘客量之比等于供应缺口的车辆数与打不到车的人数之比,则有

4)出租车保有量Q 对应可乘出租的人数为P″.根据一辆车只承载一乘客的等比例关系式,出租车需求量与城市乘客量之比等于出租车保有量与打得到车的人数之比,则有

2.2 合乘模式下车辆预测
合乘的人数为供应缺口下对应的人数P'加保有量对应的一部分人数.根据现有出租车的车座数,假定以概率p1合乘人数为2,以概率p2合乘人数为3,以概率p3合乘人数为4,合乘的车辆占保有量的β.合乘模式下的合乘车辆数为M.则有以下关系式:
1)期望合乘车辆数在占保有量的比例.合乘车辆为出租车保有量的一部分,也就是在所有的客运出租车中只有一部分具有合乘现象,其他的出租车还是通常意义下的“一乘客一车”.则有

2)合乘模式下车辆人数比等于保有量人数比.合乘模式下一辆出租车车载有的乘客数为结合概率因子下的人数期望值(即一辆车的乘客数为2p1+3p2+4p3),将合乘模式下的多人转换为“一乘客一车”模式(即一辆车的乘客数为p3).则有
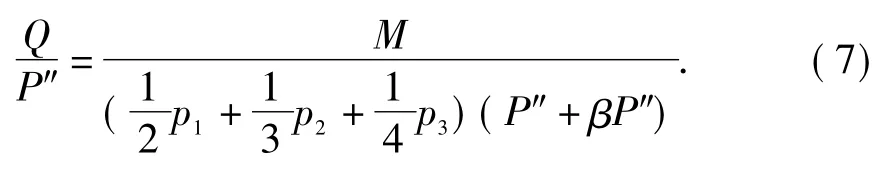
结合(8)、(9)式得合乘车辆数为
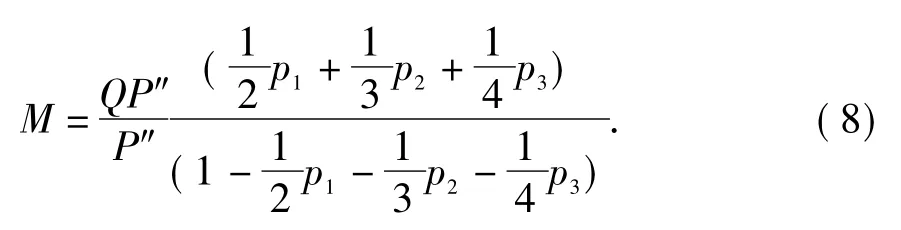
结合已知条件(6)式和(7)式,得城市出租车合乘预测为

2.3 合乘模型评价
对模型的结果进行评价,能够较为有效地检验模型的科学性和合理性,可以避免预测方法应用不当的现象.对出租车合乘需求进行预测,其误差指标要满足两个条件:反映合乘车辆数预测模型的精确度和无偏性.因此,本文选用平均误差(MAD)和平均预测误差(MFE)对模型进行评价.
平均误差这一指标是用来评价精确度、计算预测误差的.它既能用来检验预测与历史数据的吻合程度,也能用于判断预测模型是否可以继续使用的一个重要标准.平均误差用公式表示

平均预测误差是预测误差的和的平均值.如果预测模型具有无偏性,则平均预测误差公式的分子预测误差累积和应该接近于零.平均预测误差表达式

式中,Mt表示时段t 的实际值;表示时段t 的预测值;n 是整个预测期内的时段个数(或预测次数).
MAD 能较好地反映预测的精度,但不能精确地衡量无偏性;相反,MFE 能较好地衡量预测模型的无偏性,但不能精确地反映预测值偏离实际值的程度.因此,只有将两个指标综合使用,才能够避免片面的衡量,进而较为全面而准确地评价一个预测模型.
3 算例分析
为了验证基于三角模糊数的城市出租车合乘需求预测模型的实用性,本文引用一个实例进行具体分析,并在此基础上,分析各种不确定性对合乘车辆数量的影响.在不同时段点某市区对出租车的需求服从三角模糊数,六组具体数值如表格1 所示.该区的总人口为Z=820 万,在上下班高峰时段有乘出租车需求的人数占总人口的比例为a=1.38%,出租车现有保有量为Q'=11.4 万辆,政府以往会增加的供给为S=0.2 万辆,每时间段出租车使用频率为p=1.7(司机通常说的拉活的趟数),以的概率合乘人数为2,以概率V 合乘人数为3,以概率合乘人数为4.

表1 出租车的需求(万辆)
3.1 城市出租车合乘需求预测
因为城市居民出行的高峰时段是产生合乘需求量最大的时段,案例中上班高峰期8:30 左右是打车最困难的时间点,所以此时间段的需求为城市乘车需求
将以上算例中已给出的数据和前面已求得的城市乘车需求D=17.25 带入公式(11)
,经过计算得出最紧张时段的合乘车辆数为:M=11.4714 万辆(此时间段市场所供给的出租车车辆数p×Q=1.7×11.5=19.55 万辆).
3.2 合乘车辆数模型验证
参考文献《城市居民出行合乘出租车问题的研究》合乘车辆数的确定对本文模型进行验证。租车公司为满足居民合乘出行,可以确定合乘需求的出租车总量,如下关系式表达:
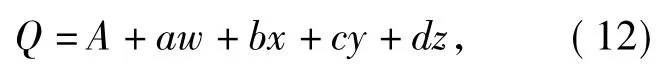
其中,Q 是出租车公司投放的满足人们合乘需求的出租车总量,A 是统计得到的相对稳定的居民合乘出租车的数量,a,b,c,d 为权重系数,w,x,y,z 分别表示当地的经济发展状况,居民出行习惯、出行总量、出租车保有量等因素。
与本文中的模型对比可知:出租车保有量、出行总量等影响因素是一致的;文献模型中提到居民出行习惯模型中乘出租车所占人口比例具有相同的本意;本文模型中的不同合乘模式下的概率包含了相对稳定的居民合乘出租车的数量这一因素,参考文献中经济发展状况这一因素较为难以衡量和评价,而本文中的区域人口数量简单易于操作,并且它也是经济发展的主要影响因素。
3.3 合乘模型评估
各时段内检测出有合乘的人数所占打的总人数的百分比,由此百分比数据计算出的合乘车辆数为实际值.运用预测误差指标评价模型的准确性,实际测量的合乘车辆数和预测模型计算出的合乘车辆数之间的差异用指标MAD 和MFE 表示,其误差指标均在0.6 以下(即合乘车辆数的预测误差小于一辆车),该评价结果显示本文中构造的综合预测模型是比较合理的.则两指标的数据如下表2所示:

表2 数据处理结果
3.4 不确定性参数对合乘车辆需求的影响
通过对模糊需求D、政府以往会增加的供给S,合乘模式下每辆出租车的车载人数的变化对合乘车辆M 的影响进行仿真,得到一些有意义的结论.
3.4.1 模糊需求对合乘车辆数的影响
根据公式(11),假设其他变量不变,研究不同模糊需求D 对合乘车辆数M 的影响.
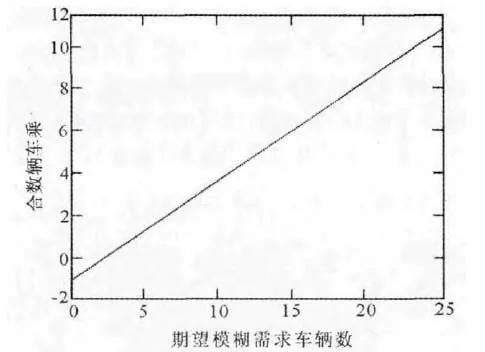
图3 (1)期望模糊需求下的合乘车辆数
图3(1)表明了模糊需求变化对合乘车辆数的影响,高的模糊需求迫使出租车客运公司持有高的车辆水平,且随着出租车苏求量本身的增大,出租车合乘的数量也相应地均匀增加.这是因为以乘客需求为中心的出租车客运管理需要在市场需求和出租车供应之间进行权衡,不能以一味地增加出租车保有量来满足城市居民的出行需求。简单地讲,人们出行选择出租车这种方式越多,与其他乘客合乘的概率越大.
3.4.2 政府年供给量对合乘车辆数的影响
根据公式(11),假设其他变量不就,研究不同政府年供给量S 对合乘车辆数M 的影响.

图3 (2)政府供给对应的合乘车辆数
图3(2)表明了政府出租车供给水平的变化对合乘车辆数的影响.高的政府供给水平使得出租车客运公司有机会持有高的车辆数水平.在相对稳定的出租车客运需求水平下,出租车合乘的车辆数会随着政府供给量地增加而相应地均匀减少.
3.4.3 每辆车合乘人数对合乘车辆数的影响
每辆车的合乘人数定义为每辆车的期望合乘人数:p1×2+p2×3+p3×4。期望值大小显然与合乘模式的概率有关。不同的合乘概率下合乘人数见下表:
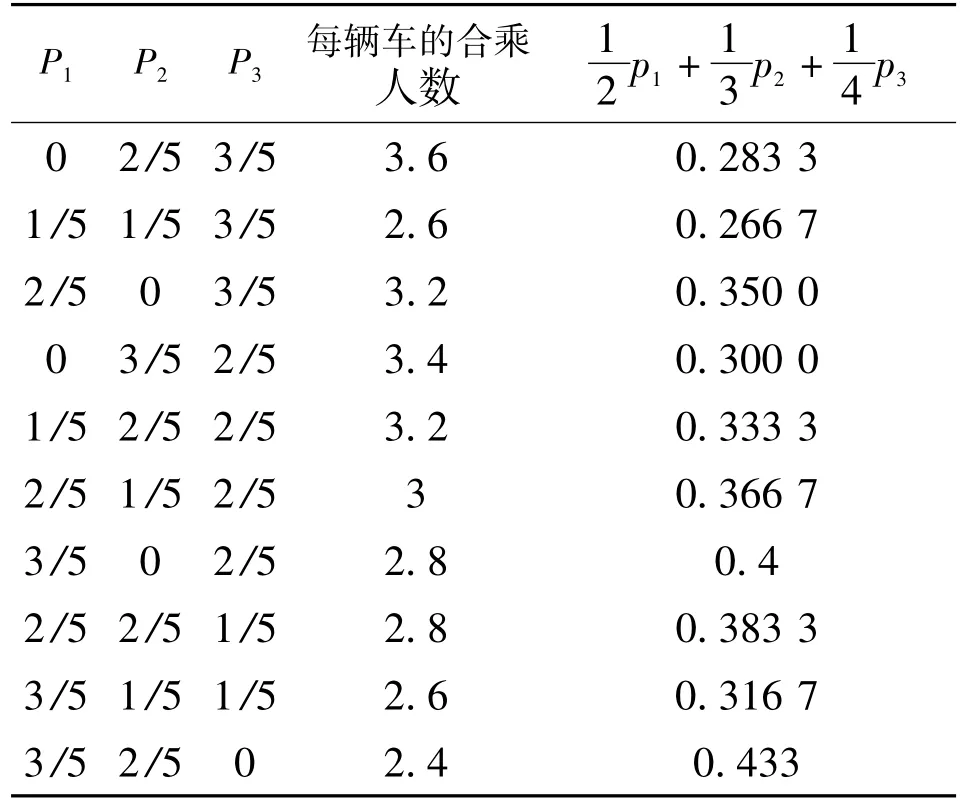
表3 数据处理结果
由上表的数据处理结果可知:合乘人数一定的情况下,合乘概率可能不同,进而导致合乘车辆数没有明显的关系.
在四人合乘概率确定的情况下,随二人合乘的概率增加,每辆车合乘人数与合乘车辆数的关系如下图所示:
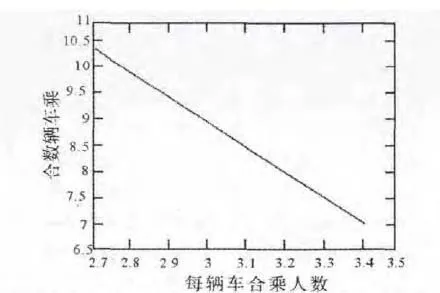
图3 (3)出租车单车合乘人数对的合乘车辆总数的影响
图3(3)表明了合乘模式下每辆出租车的车载人数变化对合乘车辆数的影响.四人合乘的概率一定的情况下,二人合乘概率越大,即人们偏向选择多人合乘这一乘车方式,要满足稳定的需求所需要的合乘车辆数就会相应减少.这一相关关私法,对缓解城市交通拥堵,增加出租车的有效利用率和环境保护等方面具有重要的现实意义.
4 结论与建议
在城市出租车的客运管理中,模糊市场需求是很难回避的现象,它们的存在使乘客的服务水平受到很大的威胁,而出租车合乘是行业应对这种情况的一种有效手段,应予以倡导推行.本文基于模糊可信性理论,研究了三角模糊需求下的出租车合乘预测的问题,主要完成了以下工作:1)建立了确定合乘车辆数的数学模型;2)探讨了市场需求、政府供给、每辆车的合乘人数的不确定性对合乘车辆数的影响.该模型同时考虑了以上三种不确定性对实现预定服务水平所需的合乘车辆数的影响,具有较强的科学性和实用性,希望能对城市出租车的科学管理提供技术支撑,为城市居民的便利出行提供政策导向.
——《2013年中国机动车污染防治年报》(第Ⅰ部分)

