圆锥曲线切线的对称轴作法

陈德华

(嘉应学院 数学学院，广东 梅州 514015)

圆锥曲线的切线作法一直是人们有着极大兴趣的课题，古往今来，人们借助于各种不同的条件，给出了圆锥曲线切线的多种作法［1～5］.本文首先探讨圆锥曲线切线的一组性质，然后借助于圆锥曲线的对称轴，利用点的对称性给出了圆锥曲线切线的一种作法.约定圆锥曲线的内部是指平面上含焦点的区域，外部是指平面上不含焦点的区域.

首先讨论椭圆的一条有趣性质.

性质1如图1，过椭圆外部的一点P，分别作对称轴的平行线与对称轴交于点Q，R，连QA，RB，分别作CA⊥AQ，DB⊥BR 与对称轴交于点C，D，分别作点C，D 关于中心O 点的对称点E，F，则点E，F在P 点关于椭圆的切点弦上.

证明设椭圆的方程为，P 点坐标为P(x0，y0)，则P 点关于椭圆的切点弦方程为b2+x0x+a2y0y=a2b2，又Q(x0，0)，A(0，a)，所以，KQA=于是AC 的方程为，则C，从而，显然点E 在切点弦上.同理可证，点也在切点弦上.由此性质，只需连接EF，就可作出P 点的切线关于椭圆的切点，从而得到点P 关于椭圆的切线，于是，有

作图问题1：已知椭圆外一点P，求作点P 关于椭圆的切线.

第一步：利用［1］中介绍的方法，作出椭圆的对称轴，中心O，长短半轴为半径的圆与椭圆对称轴的交点A，B；

第二步：过点P 分别作对称轴的平行线与对称轴交于点Q，R；

第三步：连QA，RB，分别作CA⊥AQ，DB⊥BR 与对称轴交于点C，D；

第五步：连接EF，与椭圆交于M，N 两点，则M，N就是为P 点的切线关于椭圆的切点，连接PM，PN，则直线PM，PN 就是点P 关于椭圆的切线，如图1 所示.

图1

注：当点P 在椭圆上时，问题就转化为确定切线上某点.过P 作PQ 垂直对称轴，垂足为Q；连接QA，作CA⊥AQ 与对称轴交于点C；再作点C 关于中心O 点的对称点E；连接PE，则直线PE 就是点P关于椭圆的切线，如图2 所示.

图2

下面给出双曲线类似的性质.

性质2如图3，过双曲线外部的一点P，分别作对称轴的平行线与对称轴交于点Q，R，连QA，RB，分别作CA⊥AQ，DB⊥BR 与对称轴交于点C，D，作点C 关于中心O 点的对称点E，则点E，D 在P点关于双曲线的切点弦上.

证明类似性质1 的证明可知，点E 在P 点关于双曲线的切点弦上，下证点D 也在切点弦上.

设双曲线的方程为，P 点坐标为P(x0，y0)，则P 点关于椭圆的切点弦方程为b2x0x-a2y0y=a2b2，又R(0，y0)，B(b，0)，所以于是BD 的方程为，则D(0，-，显然点D 在切点弦上.

作图问题2：已知双曲线外一点P，求作点P 关于双曲线的切线.

第一步：利用［1］中介绍的方法，作出双曲线的对称轴，中心O，实虚半轴为半径的圆与双曲线对称轴的交点A，B；

第二步：过点P 分别作对称轴的平行线与对称轴交于点Q，R；

第三步：连QA，RB，分别作CA⊥AQ，DB⊥BR与对称轴交于点C，D；

第四步：作点C 关于中心O 点的对称点E；第四步：连接ED，与双曲线交于M，N 两点，则M，N 就是P 点的切线关于双曲线的切点，连接PM，PN，则直线PM，PN 就是P 点关于双曲线的切线，如图3所示.

图3

注：当点P 在双曲线上时，问题就转化为确定切线上某点.过P 作PR 垂直对称轴，垂足为R，连接RB，作DB⊥BR 与对称轴交于点D，连接PD，则直线PD 就是点P 关于双曲线的切线，如图4 所示.

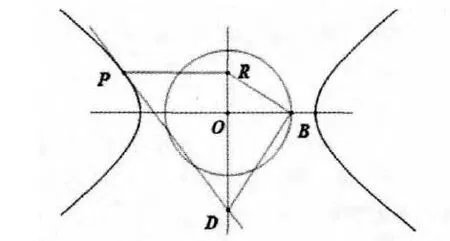
图4

最后讨论抛物线的一组性质.

性质3过抛物线外部的一点P，引其对称轴的平行线与抛物线交于点A，作P 点关于A 点的对称点P，再作QQ'垂直对称轴，垂足为Q'，作Q'关于顶点O 的对称点P'，连PP'，过Q 点作直线平行PP'与抛物线交于M，N 两点，则点Q 是切点弦MN 的中点.

证明设抛物线的方程为y2=2px，P 点坐标为P(x0，y0)，不妨取y0≠0(因为y0=0，P 点在对称轴上，结论显然成立)，则直线PQ 的方程为y=y0，于是，又PA=AQ，所以，从而，所以，kPP'=于是，过点Q 平行PP'的直线MN的参数方程可写为

将上式代入抛物线的方程y2=2px，得(y0+pt)2=

设它的两根为t1，t2，由韦达定理，有t1+t2=0，依参数t 的几何意义，则Q 为线段MN 的中点.又P点关于抛物线的切点弦方程为y0y=p(x+x0)，因为，所以MN 平行于切点弦.又M，N 在抛物线上，从而MN 就是P 点关于抛物线的切点弦.

性质4过抛物线上任意两点P，Q 的中点N引其对称轴的平行直线l，则l 必经过P，Q 的切线的交点M，且线段MN 被抛物线平分.

证明设抛物线的方程为y2=2px，P，Q 的坐标分别为P(x1，y1)，Q(x2，y2)，则于是，可求得MN 与抛物线的交点R 的坐标又切线MP，MQ 的方程分别为y1y=p(x+x1)，y2y=p(x+x2)，所以

容易验证，点R 是线段MN 的中点，所以MN 被抛物线平分.

下面利用这两条性质，给出抛物线切线的一种作法.

作图问题3：已知抛物线外一点P，求作点P 关于抛物线的切线.

此问题的关键是作出点P 的切线关于抛物线的切点.

第一步：利用［1］中介绍的方法，作出抛物线的对称轴，记顶点为O；

第二步：过点P 引其对称轴的平行线与抛物线交于A 点，作P 点关于A 点的对称点Q；

第三步：作QQ'垂直对称轴，垂足为Q'，作Q'点关于顶点O 点的对称点P'；

第四步：连接PP'，过点Q 作PP'的平行线交抛物线于M，N 两点；第五步：由性质3，则M，N 就是P点的切线关于抛物线上的切点，连接PM、PN，则直线PM，PN 就是P 点关于抛物线的切线，如图5 所示.

注：如果点P 在抛物线上，问题就转化为确定切线上某点.过P 作PQ 垂直对称轴，垂足为Q，作Q 点关于抛物线的顶点O 点的对称点P'，由性质4，则点P'在过P 点的切线上，连PP'，则直线PP'就是过P 点关于抛物线的切线，如图6 所示.

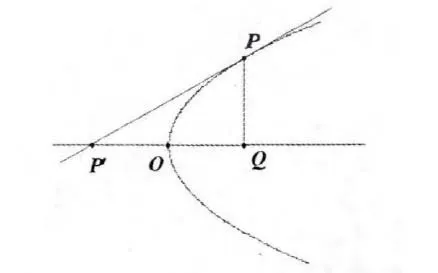
图6