轧机垂直振动三倍频颤振的分析与研究

石树正 孙丽红 王丽娜 徐 政

(1.河北建筑工程学院，河北 张家口 075024；2.张家口时代橡胶制品有限公司，河北 张家口 075024；3.河北钢铁集团宣化钢铁公司，河北 张家口 075024)

0 引 言

轧机轧制过程对轧制速度和强度有着严格的要求，生产过程中轧机辊系随机的出现垂直颤振结构失效现象.纵向颤振对产品质量影响比较突出，尤其是三倍频颤振对轧机轧制生产过程中产品影响最为严重.三倍频颤振产生的区间在120 Hz-250 Hz，有的在短时间能达到最大值，从而造成产品的薄厚不一，影响轧机的运行速度和产品质量，严重时导致产品断带.

1 对轧机三倍频颤振理论研究

如下图1所示工作辊系变形区的机械学模型.宽为B,轧制前后轧件厚度为h1和h2,速度为v1,和v2,辊的半径为R,工作辊速度为vr.由于工作辊半径比轧件厚度大(B/h>>10)，因此可以近似认为轧制前后的轧件宽度不变也为B，得：v1h1=v2h2

(1)

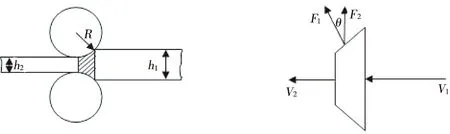
图1 轧机轧制模型 图2 轧件受力图

图3 轧机三倍频颤振模型

由于工作辊的半径远大于轧件厚度，所以轧辊的变形受力图等效为图2所示，根据式(1)中的v1h1=v2h2，F1为速度波动引起的与轧件斜面垂直波动，F2为F1的竖直分量，它影响轧制力的波动.假设运动速度的波动为余弦形式，则作用在F2上的分量也为余弦波，与实际运行轧机振动的情况相符合.

2 数学模型的建立与技术仿真

2.1 数学模型的建立分析

根据理论情况建立轧制非线性振动模型，如图3所示.

图中，轧辊的重量为m，将分析振子k1+k2x2分别定义为支撑辊分量和工作架的非线性刚度.稳定轧制时的刚度为k0，轧机工作过程中由速度变化而引起的轧制力的波动为Ecos(vt).

(2)

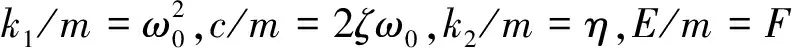
轧件张力的波动是轧机在轧制过程中速度的波动引起的，同时也影响轧制力的波动，假设上工作辊偏离心线的位移为：y=ys+Asin(ψt)

其中，ys是稳定轧制时工作辊位移，A为由于速度波动引起的振幅，ψ为垂直振动角频率.

可得：h2=h2s+2Asin(ψt)

(3)

由以上可知轧件的进口速度可表示为：

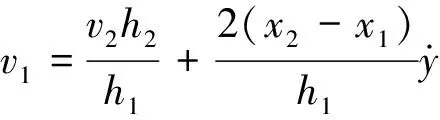
(4)

式中，L为轧件的长度,E为轧件的物理弹性模量.

其中，S为平均变形抗力，δΔ=0.7δf+0.3δb为平均张力，W为轧件的宽度，R为工作辊的半径，Δh为轧件轧制前后的厚度差.

(5)

(6)

从以上可知轧制力的不稳定，导致非线性阻尼的负阻尼特性(发散特性)，同时cΔ跟随轧制速度v2的升高显正向变化.所以，系统的垂直振动是由于后张力的不稳定引起的自激振动，振动幅度逐渐增大.

(7)

否则轧辊机架会发生三倍频颤振，同时工作辊与轧件之间出现了不稳定特性.

2.2 数学模型的仿真分析

通过建立轧机三倍频颤振数学模型，列出振动方程，然后对模型仿真分析.

图4为三倍频颤振轧机数学模型正阻尼下无激励数值仿真的时间频图和庞加莱截面图.在图中可以分析出，随着时间的变化垂直振动的幅值逐渐减小，在庞加莱截面中可看出，振动系统趋于稳定.

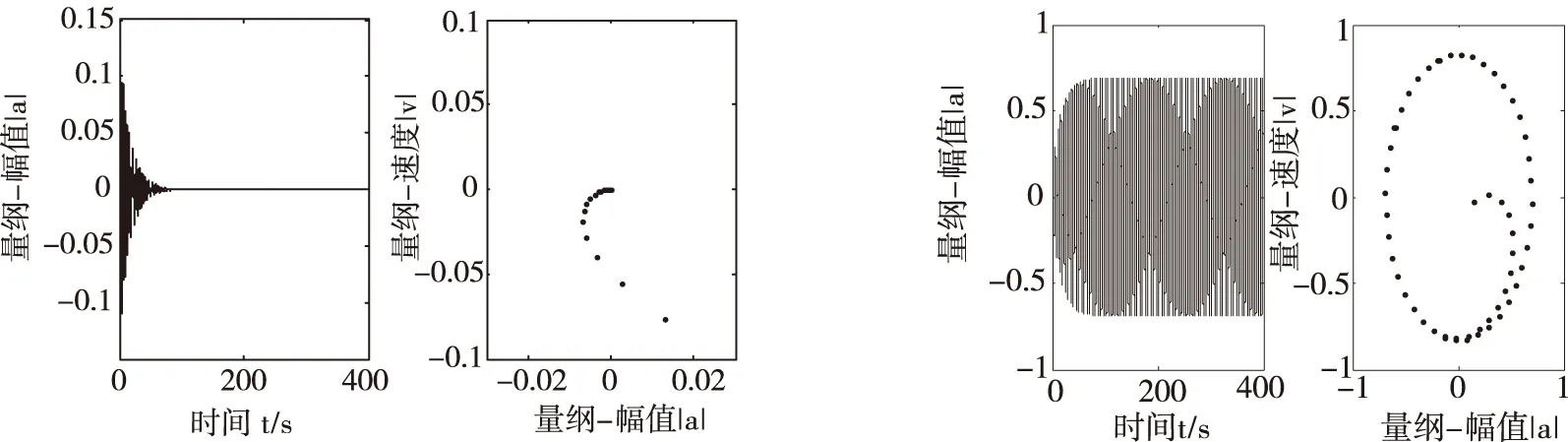
图4 正阻尼下无激励数值仿真 图5 正阻尼下有激励数值仿真

图6 负阻尼下无激励数值仿真 图7 负阻尼下有激励数值仿真

图5为轧机三倍频颤振在有激励正阻尼下的数值仿真.通过对时域图分析看出，系统振动趋于稳定，但是和外激励相比响应幅值有放大趋势，放大微弱.最终分析得出与外激励同频率的振动结果.庞加莱截面可以看出振动系统逐渐稳定.

图6为轧机三倍频颤振在无激励负阻尼下的数值仿真.通过对时域图分析看出，系统振动发散.由庞加莱载面可以看出，系统呈不稳定状态，系统发散.

图7为轧机三倍频颤振在有激励负阻尼下的数值仿真.通过对时域图分析看出，振动曲线杂乱，庞加莱截面杂乱无规律，系统不稳定.

3 结束语

根据工作中轧机轧制的垂直振动情况，分析了轧机实际受力模型和机械特点，建立了轧机轧辊的单自由度数学模型，分析三倍频颤振系统，建立数学建模并仿真.根据轧制工作面的机械受力分析，得到轧件表面产生的负阻尼效应是引起三倍频颤振的主要原因，并通过引起负阻尼的公式求出了速度对三倍频颤振的抑制方法.

参 考 文 献

[1]门艳忠.超高速机床切削颤振预报的探讨.煤矿机械.2004.3

[2]陈勇辉，刘世元，廖广兰.四辊冷带轧机三倍频颤振机理的研究.机械工程学报,2003.6

[3]闻邦椿.机械振动学[M].北京：冶金出版社，2011