离散变量结构优化的改进组合型遗传算法
谢 军 阎 杰 毕全超 朱守芹 郭鹏飞
(1.河北建筑工程学院土木工程学院,河北 张家口 075000;2.辽宁工业大学土木建筑学院,辽宁 锦州 121001)
0 序 言
遗传算法[1](简称GA)是一种基于生物自然选择与遗传机理发展起来的一种高效的随机搜索与优化的方法.遗传算法对所解的优化问题没有太多的数学要求,可以处理任意形式的目标函数和约束,无论是线性的还是非线性的,离散的还是连续的,甚至混合搜索空间;进化算子的各态历经性使得遗传算法能够非常有效地进行概率意义下的全局搜索,找到全局最优解;遗传算法对于各种特殊问题可以提高极大的灵活性来混合构造领域独立的启发式.因此,遗传算法在工业工程、经济管理、交通运输和工业设计等众多领域里获得了广泛的应用.
在工程优化问题中,经常会遇到非连续变化的一些参数,即离散变量.例如钢结构中梁、柱的板厚为有限的离散值,以及螺栓只具有有限的规格,这类优化设计问题即为离散变量结构优化设计.遗传算法在此方面已取得很多令人满意的成就,但在某些工程应用中也存在不足,比如搜索效率低、收敛于非全局最优解等.因此需针对相应问题改进基本遗传算法,同时将传统的离散变量结构优化设计方法融合到遗传算法中去,得到一种全新的混合遗传算法,其优化性能可能更佳.
本文对离散组合型法进行改进,并把离散组合型算法作为组合型操作算子融合到遗传算法中,构造一种新的离散变量结构优化算法-组合型遗传算法.运用模拟退火技术构造惩罚函数来改造适值函数,使算法更稳定地收敛于全局可行最优解.
1 数学模型的建立
以杆系结构为例,建立数学模型:
(1)
s.tgi(x)=σi-[σi]≤0(i=1,2,…,ns)
(2)
(3)
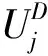
(4)
其中n是离散变量数,l是离散变量取值数.若出现各离散变量取值数不等的情况,可用某个自然数补足.一般取qij-1 本文对离散组合型法[7,8]进行改进,对其初始复合形的顶点的选择进行调整.随机方法产生的初始复合形的顶点有可能是不可行点,这可能造成需要花费过程的时间产生可行的初始复合形所需数量的顶点,导致算法的搜索效率降低. 本文按下述方法产生初始的复合形顶点:初始复合形顶点首先由随机产生,然后进行结构分析.若该顶点的第i个设计变量不满足对应的应力约束条件,且设计变量值的序号不等于n,表示该杆的几何尺寸不满足要求,可取该变量值下一个序号所对应的变量值.再进行结构分析,所有的应力和位移约束条件都必须满足.若不满足,重复上述步骤,直到满足为止;若满足,说明该点为可行点,继续找出构造初始复合形所需的可行点为止. 把离散组合型算法作为组合型操作算子融合到遗传算法中,构造一种新的离散变量结构优化算法-组合型遗传算法. 组合型遗传算法中,采用模拟退火技术构造惩罚函数来改造优化函数,将式(1)这种约束优化问题转化为式(5),即无约束优化问题 (5) 其中P(rk,X)是惩罚函数,rk是惩罚因子.本文P(rk,X)采用的具体形式是 (6) 其中rk=1/T(t),T(t)是模拟退火算法中的冷却进度表,本文采用的降温方式是 T(t)=T0/1+t (7) 式(5)为求解函数的极小值问题,将其改造成适值函数,适值函数为 F(X)=FP(X)max-FP(X) (8) 式中FP(X)max表示每一代种群的所有个体中目标函数的最大值. 达尔文进化论说明,初始种群的好坏决定着进化的方向.那么对于改进的组合型遗传算法,其初始种群决定优化的结果.因此其初始种群的个体,一部分可由改进的组合型遗传算法的优化解,其它的可随机产生.而改进的组合型算法的优化解当然是可行的,适应能力强,可以增强种群的竞争机制,推动整体寻优能力. 进化过程中,遗传算法的每一代种群的所有可行个体作为组合型算法的初始点进行局部性的搜索.同时种群个体按照适应度排序,采用最优个体保留策略直接复制到下一代,而适应度最差的那些个体由组合型算法搜索到的优良个体替换.那么下一代种群中继承了上一代的优良基因,而不良基因被淘汰,且其基因一般比上代更优,即寻优能力更强;且每一代种群个体是由遗传算法和组合型算法共同产生,保持了种群的多样化.种群的每一代再整体经过遗传算法的复制、交叉和变异等操作进行全局性的搜索.可以看出,遗传算法和组合型算法混合在一起,可以独立寻优,也需互相合作共同寻优. 图1 组合形遗传算法程序框图 图2 十杆钢桁架 十杆钢桁架如图2所示,杆件全部采用文献[9]中的单根热轧等边角钢,杆件的截面型号有16种,即每个变量有16个离散值:{113.2,143.2,145.9,174.9,185.9,235.9,265.9,297.1,308.6,334.3,338.2,497.8,507.6,736.7,791.2,1063.7}(mm2),钢材的E=200 GPa,ρ=77 kN/m3,许用拉、压应力分别为[σ+]=150 MPa和[σ-]=100 MPa.结构承受两种工况:Ⅰ:p1=40 kN,p2=0 kN;Ⅱ:p1=60 kN,p2=20 kN,表1为结构优化结果,并与文献[2]中所用方法的优化结果比较. 表2 结构优化结果 与基本遗传算法和组合型算法的计算结果比较证明:把离散组合型算法作为组合型操作算子融合到遗传算法中,构造的离散变量结构优化算法-组合型遗传算法,优化效果良好.改进的组合型遗传算法具有局部搜索快和全局性好的双重特点,是可行且有效的离散变量结构优化设计方法. 参 考 文 献 [1]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999,34~37 [2]谢军,郭鹏飞,等.离散变量结构优化的组合形遗传算法[J].辽宁工学院学报,2006,26(5):311~315 [3]郭鹏飞.离散变量结构优化的斐波那契遗传算法[J].辽宁工学院学报,2002,23(1):1~4 [4]郭鹏飞,韩英仕.离散变量结构优化设计的拟满应力遗传算法[J].工程力学,2003,20(2):95~99 [5]朱朝艳,刘斌,郭鹏飞.离散变量结构优化设计的复合形遗传算法[J].东北大学大学学报,2004,25(7):689~691 [6]张延年,刘斌,朱朝艳,等.离散变量优化设计的改进斐波那契遗传算法[J].机械强度,2006,28(1):55~60 [7]陈立周,路鹏,孙成宪,等.工程离散变量结构优化设计[M].北京:机械工业出版社,1989,43~44 [8]陈立周.机械优化设计方法[M]第3版.北京:冶金工业出版社,2005,205~214 [9]孙训方,方孝淑,关来泰,等.材料力学(上册)[M]第3版.北京:高等教育出版社,1994,420~435 [10]玄光男,称润伟.遗传算法与工程设计[M].北京:科学出版社,2000,1~28 [11]白新理,等.结构优化设计[M].郑州:黄河水利出版社,2008,171~1862 改进的离散组合形法
3 组合形遗传算法
3.1 基于模拟退火罚函数的适值函数
3.2 种群的形成和进化过程
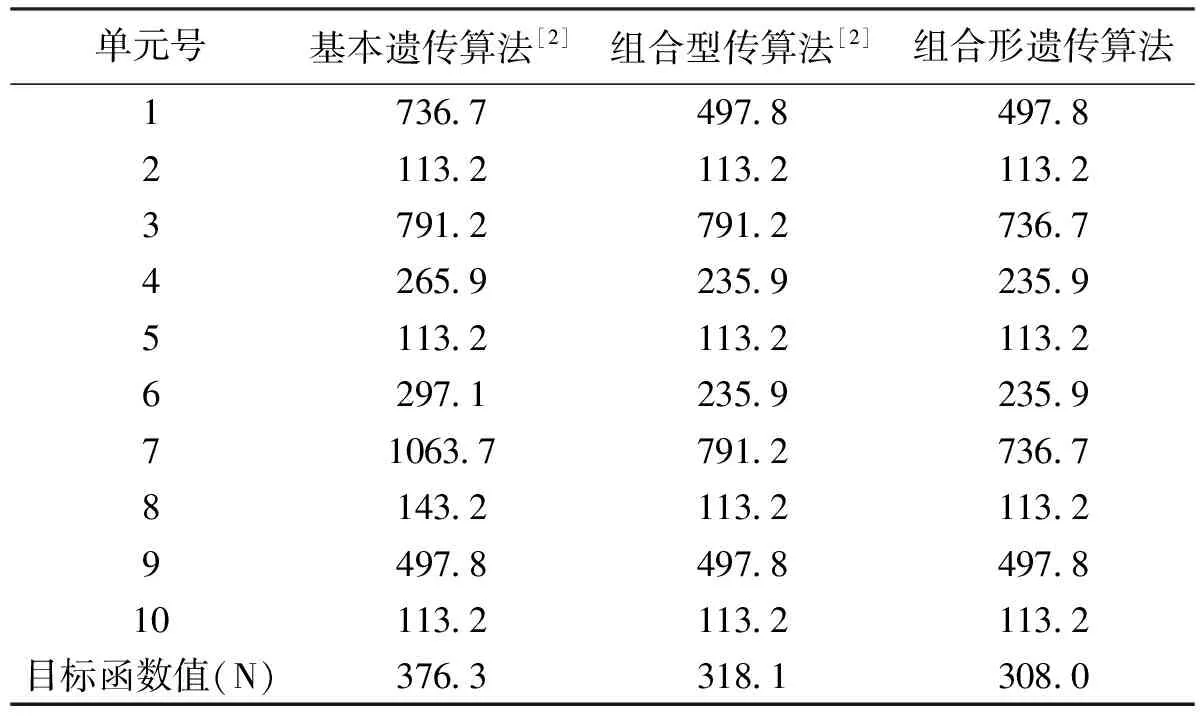
4 算 例

5 结 论

