自适应邻域选择的I somap算法

李燕燕 肖 丹 魏晓峰 王海东

(河北建筑工程学院，河北 张家口 075024)

0 引 言

随着信息时代的到来，高维数据以更加丰富的形式来描写着现实世界，并且已深入到各个领域.然而，高维数据中包含了大量的冗余信息，并且不容易被人们表示和处理，更无法感知数据内在的本质规律，所以要在保持原始高维数据的本质信息的前提下得到高维数据的低维表示.在这种背景下，数据降维技术应运而生，其实质是揭示高维数据内在的本质信息，挖掘出隐藏在高维空间中数据的低维本征表示.

在降维的发展历程中，首先被提出来的是线性降维方法，线性降维方法是数据集在线性结构的假设下提出的，目的是使得原高维数据之间的线性关系在低维空间中也是保持不变的.现有的线性降维方法有：主成分分析(principal component analysis，简称PCA[1])、多维尺度变换(Multidimensional Scaling，简称MDS[2]).这些线性降维方法运算简便、复杂度低、有利于线性结构的数据降维.然而，各个领域中高维数据多表现为非线性的，从而又兴起了解决高维非线性数据的降维方法，流形学习作为非线性降维的一种技术广泛应用于模式识别的各个领域.著名的流形学习算法有等规度映射ISOMAP[3](Isometric Mapping)、局部线性嵌入(Locally linear embedding，LLE[4])等.ISOMAP把任意两点之间的测地线距离作为流形的几何描述，能有效地避免短路问题，但是拓扑稳定性差，且容易受到流形稀疏的影响.LLE是一种局部优化算法，以局部线性信息的重叠来达到学习全局非线性信息的目的.

然而，Isomap在处理稀疏数据时，近邻点的选取很有可能造成“短路”现象，因此，本文通过邻域选取算法自适应的动态选择每一个样本点的邻域大小，再使用聚类信息来汇聚相似的样本点，保证了降维后的数据具有很好的可分性.实验结果表明，将该算法能成功应用于手工流形的降维，取得了很好的效果.

1 Isomap算法

1.1 Isomap算法的思想

Isomap的理论框架是MDS，不同之处是对数据之间相似性的衡量由原始欧式距离换成了测地线距离，通过这种整体几何特征的重构来最大程度的保持数据降维前后的整体拓扑结构.

算法的关键是正确的描述高维非线性空间中样本点间的距离，它认为传统的欧式距离不能代表样本点间的实际距离，而沿着数据流形区域分布的测地线距离能够更好的描述样本点间的内在关系.由于测地距离一般能够内在地反映流形的本质几何机构，所以Isomap通常能有很好的降维效果.Isomap的主要步骤如下：

Step1：构建近邻图G.主要用k近邻的方法确定xi邻域点xj.

Step2：计算近邻图G上成对的测地线距离.当图G有边xixj，设最短路径dG(xixj)=d(xi,xj)；否则设dG(xixj)=∞.则测地距离定义如下：

Step3：用多维尺度变换MDS求解流形的低维表示Y.

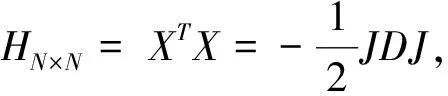
1.2 Isomap对稀疏数据失效的原因

对Isomap算法的分析可知，Isomap通过近邻算法构建近邻图，在数据稀疏的情况下，流形上样本点数目分布相对分散，k近邻算法的搜索范围相对扩大，可能将本不属于同一流形区域的点包含在同一近邻图中，从而导致短路现象，即流形上本不相邻的两个数据点成为近邻点.短路的出现可能使得拟合出的测地线距离严重偏离数据流形区域，难以正确反映高维数据的整体拓扑结构.

2 A-Isomap算法

2.1 算法思想

在数据稀疏的情况下，近邻图中短路边的出现是导致算法失效的重要原因，算法CN-Isomap通过对“流形邻居”的设定来鉴别和删除近邻图中短路边[5]，极大地削弱Isomap对邻域大小的依赖程度，并使其更具拓扑稳定性.本文在CN-Isomap算法的基础上，在近邻区内进行聚类分析，使相似的样本点汇聚在一起，保证了降维后数据具有很好的可分性.

聚类算法：利用k均值聚类后的各类中心以及总体样本中心信息来构建样本的数据可分系数，来约束测地距离.设样本点聚类分类的类别个数为C，mj为第j类样本的中心，n(j)为第j类样本的个数.则第j类样本点的类内平均距离为

(1)

第j类样本与总体样本中心的距离为

(2)

m为总体样本的中心.根据式(1)和(2)，我们定义样本点重构误差的近似重构系数为

(3)

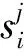
2.2 算法的主要步骤

Step1：利用k邻域法找到样本点的近邻点集合.

Step2：构建k个样本点的近邻图，并利用“流形邻居”算法，删除短路边.

Step3：在近邻区内进行聚类分析，利用数据可分系数将不同类别的流形分开.

Step4：应用最短路径算法得到任意两样本点间的最短路径距离，用这个距离来估计样本点间的测地线距离，完成对任意两点测地线的拟合.

Step5：将这些最短路径长度作为输入运行古典MDS算法，完成降维.

3 实验结果分析

3.1 手工流形实验

本实验采用的是经典的Swiss roll手工流形数据集，近邻点k=6，利用相同颜色的点标识近邻状态.下面两图呈现了采样数据点个数均为1000点和300点时各种算法的2维嵌入结果.

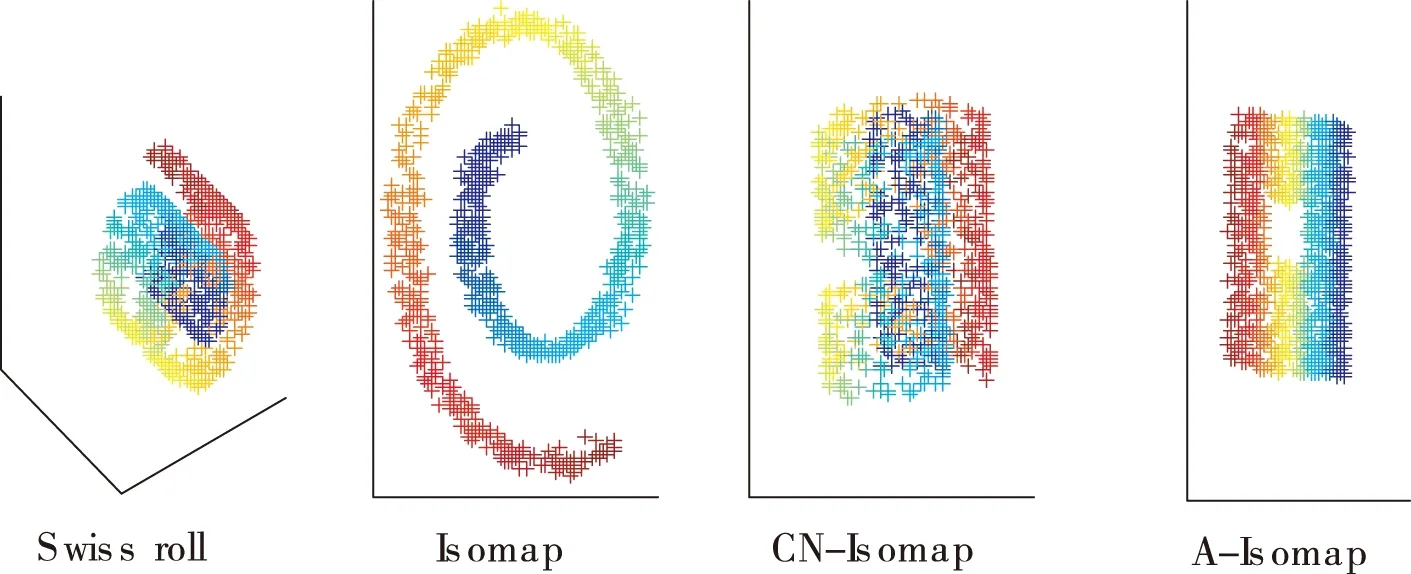
图1 采样点个数1000时的二维嵌入效果

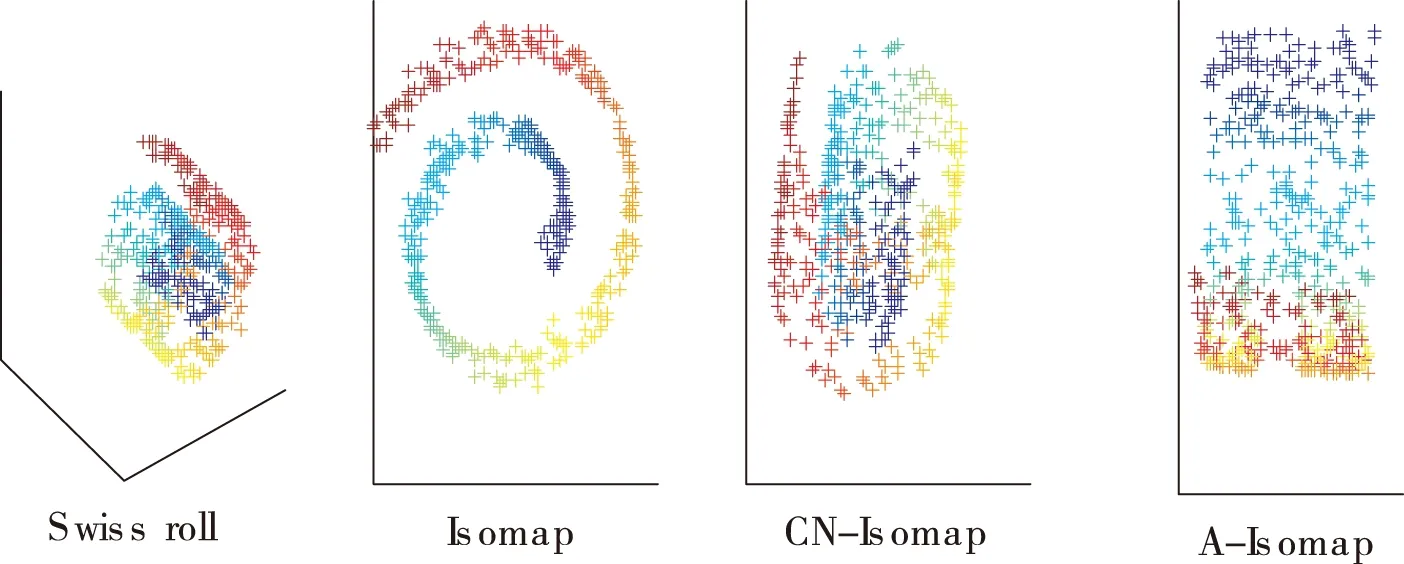
图2 采样点个数300时的二维嵌入效果

在数据集稠密的情况下，A-Isomap的降维效果优于Isomap和CN-Isomap，特别在数据稀疏时，Isomap和CN-Isomap算法很难保持数据间潜在的低维结构，降维后的二维数据呈现出了扭曲变形.而本文新算法A-Isomap却能在原数据空间数据信息量少的条件下，可以较好的保持数据间的相互关系.

3.2 算法效率分析

在Isomap算法中.影响时间复杂度的因素主要有3个：选取近邻所用的时间、计算最短路径所用的时间、计算特征向量所用的时间，这三者的时间复杂度分别是O(mN2)、O(kN2logN)、O(N3).CN-Isomap虽然增加了对流形邻居甄别、删除的时间，但是却减少了最短路径计算的时间.对比之下，增加的时间复杂度对算法的影响很小.本文算法A-Isomap在CN-Isomap的基础上，对邻域区内的点进行了聚类分析，其时间复杂度是O(kNt)，其复杂度是远远小于O(N3).其中，N维样本点的个数，m维输入空间的维数，k为近邻点的个数，t为迭代次数.通过表1各算法的平均时间比较可以看出，本文新算法A-Isomap的平均计算时间并没有显著的增加，而是和前两种算法相差无几.

表1 平均计算时间比较(单位/秒)

4 小 结

A-Isomap算法针对稀疏数据局部信息量不足的问题，通过邻域选取算法自适应的动态选择每一个样本点的邻域大小.同时，使用聚类信息来汇聚相似的样本点，保证了降维后的数据具有很好的可分性，加强了局部结构的刻画，通过实验结果展示出A-Isomap能够更好地保持稀疏数据的拓扑结构，更具鲁棒性.

参 考 文 献

[1]Jolliffe I.Principal component analysis[M].John Wiley & Sons,Ltd,2005

[2]Cox T,Cox M.Multidimensional Scaling.1994[J].Chapman&Hall,London,UK

[3]J.B,TENENBAUM,V.DE SILVA,J.C.LAGFORD.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319～2323

[4]S.T.ROWEIS,L.K.SAUL.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323～2326

[5]武森，全喜伟，陈学昌.稀疏数据非线性降维的CN-Isomap算法[J].数学的实践与认识，2010,40(17):182～188