造船供应链利益分配问题的Shapley值法分析

范德成, 胡钰

(哈尔滨工程大学 经济管理学院，黑龙江 哈尔滨 150001)

造船供应链是指以造船企业为核心，由供应商、协作厂、分段厂等相关企业或机构，为满足船东需求而形成的供需网络，其中各节点企业的有效合作是造船供应链存在的核心，互惠互利是长期合作的基础和前提条件。目前专门研究造船供应链利益分配的文献较少，孙彦等应用合作n人对等理论从利益分配的角度为造船供应链合作伙伴的选择提供思路[1]；陈超等利用不对称Nash谈判模型构建了造船供应链的利益分配机制[2]；马红燕等应用不对称Nash谈判模型设计了造船供应链合作利益分配的协商机制[3]。鲜有学者在该研究领域采用Shapley值法，而在供应链利益分配研究维度，较多学者运用了Shapley值法及其改进方法进行定性和定量分析，如Corbett等依据供应链成员企业的业绩状况和努力程度来确定成员企业的利益分配系数[4]；戴建华等在Shapley值法的基础上引入风险因子对供应链动态联盟伙伴企业的利益分配进行协调[5]；马士华等在Shapley值法中引入技术创新激励指数对供应链各成员企业的收益分配进行调整[6]。

由于造船供应链中所有的相关企业都是相互独立的利益主体，其加入造船供应链的主要目的便是实现最大化的利益获取，因此，如何设计和协调各参与主体的利益是造船供应链管理的关键问题。对利益分配的定量研究有多种方法， 但Shapley值法及其改进模型能够测算多主体合作的利益分配成果。从已有的研究成果来看，采用Shapley值法分配某行业供应链各节点企业利益的做法将是未来研究的主要趋势[7]。该方法能在利益分配的研究中体现各节点企业在整体收益中获得的风险补偿、技术创新能力对核心竞争力的提升效益以及成员的投资详情和合作程度。因此本文借助Shapley值法在供应链合作联盟中的建模思想，结合造船供应链的特点和相关企业间的互动关系，构建了造船供应链的利益分配模型，在对原始Shapley值法掌握的基础上，加入风险因子、技术创新激励和资源投入量3个影响供应链利益分配的因素对Shapley值法进行改进，以解决造船厂、供应商和协作厂等相关企业间的利益分配问题[8]。

1 Shapley值法模型及其改进

1.1 Shapley值法模型

设n个企业构成了一个供应链企业集合N(N=1，2...n)，这其中的一些子集S组成联盟，假设供应链企业合作联盟N的实值函数为v(N)风险管理收益，则合作联盟S的风险管理收益为实值函数v(S)。集合N中的任一子集S都满足条件：

在以上条件中，只有供应链创造的总价值大于每个成员单独创造的价值之和，即v(S1∪S2)≥v(S1)+v(S2)，才能保证企业加入供应链参与建立合作联盟是有利可图的。

设定φi(v)是集合N中的成员i从供应链合作利益v(N)中获取的收入，则合作关系的分配情况可以表示为Φ(v)=(φ1(v),φ2(v)...φn(v))，合理的合作利益分配方案要满足条件：

在集合N合作的前提下，用Shapley值法确定的各个伙伴i获得的利益分配值为：

(1)

(2)

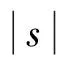
1.2 Shapley值法的局限性

根据对Shapley值法内涵和模型原理的理解，Shapley值法的核心思想强调价值的贡献，该思想仅考虑到合作企业对合作联盟整体维度的贡献，仅从价值贡献率的角度考虑供应链的利益分配情况。该方法建模的初始条件便是假定各成员企业的风险承担、技术创新能力以及合作过程中各供应商的资源投入都是一样的，而在现实的供应链运作中，这种假定是不成立的。

通常情况下，供应商合作联盟中各成员企业承担风险的能力、技术创新能力以及为供应链投入的资源成本是不同的，各成员企业的合作态度也必定存在差异。因此，为了更加全面系统地研究造船供应链的利益分配议题，需要对Shapley值法进行改进，按照风险补偿原则、技术创新激励原则和收益与投入资源相对称原则，引入风险因子、技术创新激励指数和资源投入量分别对各合作企业需要承担的风险因素、技术创新带来的激励影响以及供应商合作引起的资源整合作用进行定量表示[9]。

1.3 Shapley值法模型的改进

在文献[5]基础上，本文在Shapley值法模型的改进中加入风险因子R要素。在实际供应链中，各合作成员企业要承担内生和外来两部分风险，影响利益分配的风险种类主要有：生产风险(如生产组织与采购风险、分销商选择风险和物流运作风险等)、市场风险(如市场的不确定性需求风险、市场内的信息传递风险等)、政策风险(如经济政策风险、法律环境风险等)、合作风险(如合作企业文化差异产生的风险、企业道德风险等)。

设成员企业i在供应链运作中实际需要承担的风险因子为Ri(i=1,2...,n) ，成员企业i承担的风险因子计算为：

(3)

实际分配利益值为

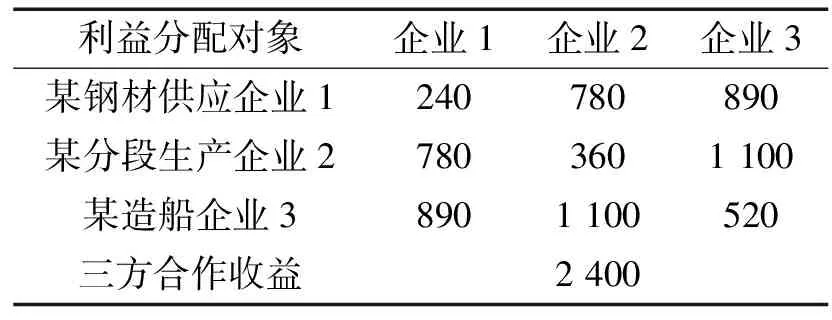
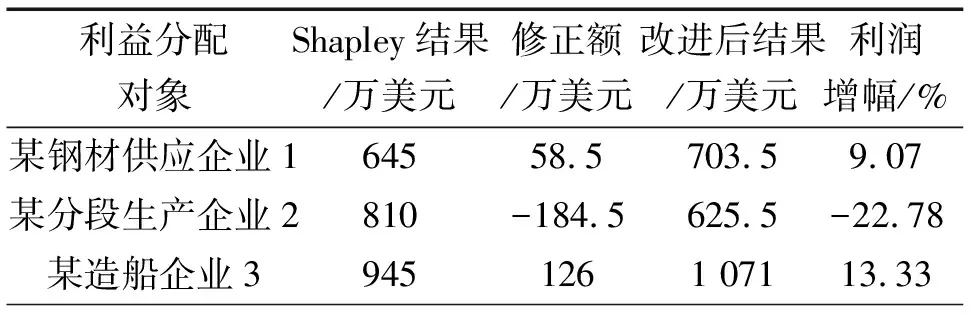
在文献[6]基础上，本文也在Shapley值法模型的改进中加入技术创新激励指数j要素。设成员企业i通过技术创新为供应链创造的收益为qi，则供应链上所有成员企业通过技术创新而创造的收益为∑qi，根据供应链所处行业对技术创新的要求差异，各成员企业可以接受的激励指数为j(0

在考虑技术创新激励指数的影响作用下，供应链成员企业i在实际合作中获取的利益分配修正量为

实际分配利益值为

qi/∑qi<1/n时，成员企业i技术创新成果不突出，相应利益会在原有分配计划中减少；qi/∑qi>1/n时，成员企业i技术创新成果突出，相应利益会在原有分配计划中增加；qi/∑qi=1/n时，成员企业i的利益获得与原有分配计划相同。

在文献[10]基础上，本文也在Shapley值法模型的改进中加入资源投入量C要素。设成员企业i在供应链合作中投入资源Ci(i=1,2...,n)，则供应链上所有成员企业资源投入的总和为∑Ci，每个成员企业的资源投入在所有成员企业资源投入总和中占有的比重是Ci/∑Ci，成员企业i的资源投入与所有成员企业的平均资源投入差值为

在考虑资源投入量的影响作用下，供应链成员企业i在实际合作中获取的利益分配修正量为

实际分配利益值为

Ci/∑Ci<1/n时，成员企业i的资源投入量较少，相应利益会在原有分配计划中减少；Ci/∑Ci>1/n时，成员企业i的资源投入量较多，相应利益会在原有分配计划中增加；Ci/∑Ci=1/n时，成员企业i的利益获得与原有分配计划相同。

综上所述，依据改进的Shapley值法模型，供应链成员企业i在实际合作中获取的利益分配总修正量为

实际分配利益总值为

经过运算得

因此改进后的实际利益分配模型符合要求。

1.4 模型参数的确定

在综合考虑风险因素、技术创新激励和资源投入量影响作用的基础上，用信息熵来测定风险因素的大小；用技术资本和人力投入比例来衡量技术创新激励指数；用合作投入状况来评定供应链各成员企业的合作程度；应用AHP法或模糊数学方法确定三要素各自的权重大小；还可采用调查问卷的形式应用Likert量表法定性确定模型的参数[11-12]。

2 应用实例

2.1 模型参数的确定

由于船舶行业的特殊性，分段厂的存在情况根据船市的具体状况而定，且造船企业即销售船舶的主体收益也会根据船市状况有所变动。假设当前船市处于乐观水平，分段厂能够独立且长期存在，此时造船企业销售巴拿马级散货船的利润收益为船价的20%左右，根据近年来巴拿马级散货船的销售均价约为2 600万美元计算，则造船企业3的销售收益约为520万美元，其他成员企业的利益分配情况见表1。

表1 造船供应链中成员企业的利益分配情况

2.2 Shapley值法基础利益分配额的确定

根据Shapley值法的利益分配公式，可得出造船供应链各成员企业基于Shapley值法的利益分配额，某钢材供应商企业1的基础利益分配额φ1(v)的计算过程如表2。

表2 某钢材供应企业1的基础利益分配额φ1(v)计算表

由表2可得，某钢材供应企业的基础利益分配额φ1(v)=80+70+185/3+1 300/3=645万美元，同理，可得某分段生产企业的基础利益分配额φ2(v)=810万美元，某造船企业的基础利益分配额φ3(v)=945万美元。可见，经过合作后，造船供应链的各成员企业均能获取额外的利润，且满足集合N中的任意两家合作得到的收益都大于两者单独获益的和，此外，也满足 ：φ1(v)+φ2(v)+φ3(v)=v(N)=2 400万美元；φ1(v)>v(1)、φ2(v)>v(2)、φ3(v)>v(3)，即各成员企业获取的基础利益分配方案均满足前文所述的合作条件。

2.3 实际利益分配额的确定

1)设定改进Shapley值法原始模型所需的变量值。

结合上述造船供应链中各成员企业的收益等实际情况，设定成员企业在供应链运作中实际需要承担的风险因子分别为：R1=0.42，R2=0.21，R3=0.37；造船供应链中各成员企业对技术创新的需求高低各异，在实际操作中，一般情况下钢材供应企业和造船企业对技术创新的需求较分段生产企业的技术创新需求高，而建造军用船舶和民用船舶的技术创新需求指数也存在较大差异，为便于实证运算，本文假设上述造船供应链中各成员企业可以接受的技术激励指数j=0.55，此外，假设各成员企业通过技术创新而创造的收益分别为：q1=630万美元、q2=450万美元、q3=720万美元；同时，假设上述造船供应链中每个成员企业的资源投入量在所有成员企业资源投入量总和中占有的比重分别是：0.31、0.33和0.36。

2)利用设定的改进参数计算上述造船供应链中各成员企业的利益分配修正量和实际的利益分配额。经过计算可得：

3)将改进后的利益分配方案与基础利益分配方案进行对比分析。

从表3中可以看出，改进后的利益分配方案使造船供应链中负责对船舶分段装配、对整装船舶进行测试及最终销售的造船企业3获利最大，利润水平上升了13.33%，较单独经营时有近3倍的利润增加；为船舶建造提供钢质原材料的钢材供应企业1在造船供应链中分得的利益额有所增加，尽管增加幅度较小，为9.07%，但较单独经营时也有多于两倍的收益量；而负责对钢材进行模块化建造的分段生产企业2收到了损失，利润水平下跌了近5成，但与单独经营时的收益相比却有明显的提升。

表3 改进的利益分配方案与基于Shapley值法的基础利益分配方案的比较

对于本文造船供应链利益分配方案中的3个主体，分段生产企业2在技术投入和风险承担方面都比钢材供应企业1和造船企业3承受的少，故在Shapley值法改进利益分配方案的过程中，分段生产企业2获得的利润有所降低，这符合“高风险高收益”的经济规律，也印证了高技术投入能够提高利润水平的原则。在资源投入方面，造船企业3较钢材供应企业1的基础投资额多，在最终利益分配方案和改进后的利益分配方案中，造船企业3获得的利益分配都多于钢材供应企业1，这满足按投资额和贡献度分配利益的原则要求。

改进后的利益分配方案与现实情况是相符的。在实际的船舶生产和经济贸易中，原材料供应商、分段生产企业和造船企业的合作往往能获得较高的利润。可见本文提出的利益分配方案在理论上具有合理性，在实践上具有应用性，这一切实可行的利益分配方案能够兼顾各成员企业的收益公平，保证各方利益，对提高造船供应链各成员企业的合作效率，齐头并进实现经济和社会效益的增长具有借鉴价值。

3 结束语

本文以造船供应链中钢材供应企业、分段生产企业和造船企业为研究对象，探讨了基于Shapley值法及其改进模型的合作伙伴利益分配思路和方法。改进后的利益分配方案在原始方案的基础上考虑了风险因素、技术创新激励和资源投入量对利益分配的影响，形成更为科学合理且公平的利益分配结果，该研究成果在理论上和实践上都具有一定的指导意义。

本文对Shapley值法的改进仅考虑了风险因素、技术创新激励和资源投入量对利益分配的约束，而影响供应链各成员企业利益分配的因素众多，其他因素的作用关系会改变利益分配模型的相关参数，进而影响最终的利益分配结果，这也是本文研究的局限性所在；此外，本文仅选择了钢材供应企业、分段生产企业和造船企业3个主体，这一研究结论可能并不适用于造船供应链中其他的节点企业。未来研究将进一步围绕造船供应链利益分配这一研究方向，运用其他方法进行实证分析和调研，以获取更为严谨且实用的研究结论。

参考文献：

[1]孙彦，张光明，盛永祥.应用合作n人对等理论选择船舶供应链合作伙伴[J].华东船舶工业学院学报，2003，17(6)：84-88.

SUN Yan,ZHANG Guangming,SHENG Yongxiang. Partner selection of shipbuilding supply chain based onncooperative game theory[J]. Journal of East China Shipbuilding Institute,2003,17(6):84-88.

[2]马红燕，张光明.造船供应链合作利益分配协商机制研究[J].船舶工程，2007(2)：69-72.

MA Hongyan,ZHANG Guangming.Study on bargain mechanism of cooperative benefit allocation of shipbuilding supply chain[J].Ship Engineering, 2007(2):69-72.

[3]陈超，裴春.基于不对称Nash协商模型的多Agent造船供应链协商机制研究[J].价值工程，2010(13)：23-25.

CHEN Chao,PEI Chun.Research on negotiation mechanism of multi-agent shipbuilding supply chain based on asymmetric Nash negotiation model[J].Value Engineering,2010(13):23-25.

[4]CORBETT C J,GROOLE X.A supplier’s optimal quantity discount policy under asymmetric information[J].Management Science,2000,46(3): 441-450.

[5]戴建华，薛恒新.基于Shapley值法的动态联盟伙伴企业利益分配策略[J].中国管理科学，2004，12(4)：33-36.

DAI Jianhua,XUE Hengxin.The strategy of profit allocation among partners in dynamic alliance based on the shapley value[J]. Chinese Journal of Management Science,2004, 12(4):33-36.

[6]马士华，王鹏.基于Shapley值法的供应链合作伙伴间收益分配机制[J].工业工程与管理，2006，4：43-46.

MA Shihua,WANG Peng.The study of profit allocation among partners in supply chain based on the shapley value[J].Industrial Engineering and Management,2006,4:43-36.

[7]郑鑫，朱晓曦，马卫民.基于Shapley值法的三级闭环供应链收益分配模型[J].运筹与管理，2011，20(4)：17-22.

ZHENG Xin,ZHU Xiaoxi,MA Weimin. Revenue distribution model of three echelon closed-loop supply chain based on shapley-value[J].Operations Research and Management Science,2011,20(4):17-22.

[8]SAHIN F,ROBINSON E P.Flow coordination and information sharing in supply chains:review, implications,and directions for future research[J]. Decision Sciences, 2002,33(4): 505-536.

[9]SHAPLEY L S．Cores of convex games[J]. International Journal of Game Theory,1971, 1(1):11-26．

[10]高洁，周衍平.Shapley值在植物品种权价值链利益分配中的应用[J].运筹与管理，2012，21(2)：168-172.

GAO Jie,ZHOU Yanping.Application of the Shapley value to profit allocation of plant variety right value chain[J].Operations Research and Management Science,2012,21(2): 168-172.

[11]孙世民，张吉国，王继永.基于Shapley值法和理想点原理的优质猪肉供应链合作伙伴利益分配研究[J].运筹与管理，2008，17(6)：87-91.

SUN Shimin,ZHANG Jiguo,WANG Jiyong. Study on profit allocation among partners in high quality pork supply chain based on the Shapley value and Ideal point principle[J].Operations Research and Management Science,2008,17(6): 87-91.

[12]吕萍，张云，慕芬芳.总承包商和分包商供应链利益分配研究—基于改进的Shapley值法[J].运筹与管理，2012，21(6)：211-216.

LYU Ping,ZHANG Yun,MU Fenfang.Study on profit distribution of general contractor and subcontractor in construction supply chain-based modified Shapley value[J].Operations Research and Management Science,2012,21(6): 211-216.