高速电磁阀动态响应特性响应面预测模型的研究
刘鹏,范立云,马修真,王昊,白云,宋恩哲
(哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001)
电控单体泵是目前应用于柴油机上,最适合中国国情的,能够满足欧三排放法规具有欧四潜力的,同时可以改善燃油经济性的时间控制式燃油喷射系统[1-5]。高速电磁阀是电控单体泵能否正常工作的最关键的部件之一,其动态响应特性直接影响了喷油量和喷油定时的控制精度,进而对柴油机的动力性、燃油经济性和排放物的稳定控制产生影响。高速电磁阀是一个电、磁、机、液耦合的复杂机构,采用传统的试验方法对其研究需耗费巨大的人力物力,且产品开发周期长,而预测研究正为高速电磁阀动态响应特性的研究提供了新思路。本文通过数值模拟并结合响应面方法及实验设计思想,得出了高速电磁阀动态响应特性的响应面预测模型。
1 电磁阀结构组成和工作原理
电控单体泵高速电磁阀的结构如图1所示。主要包括电磁铁、衔铁、控制阀杆、衔铁复位弹簧、出油堵头等零部件。其中,电磁铁主要由铁芯、励磁线圈、外壳等组成。通电后,电磁铁吸合衔铁,拉动控制阀杆,关闭密封锥面,切断燃油回路,从而在泵腔内建立起燃油喷射所需的高压;断电后,复位弹簧迫使衔铁推动控制阀杆复位,开启密封锥面,卸载高压燃油,停止燃油喷射。其对喷油量和喷油定时的控制通过调节控制阀杆的闭合时间和闭合时刻来实现[6]。

(a) 电控单体泵
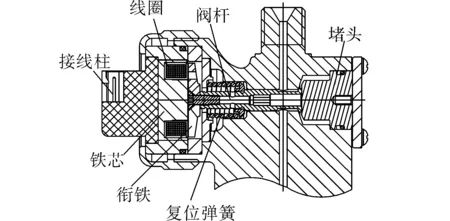
(b) 电磁阀
2 高速电磁阀仿真模型的建立
本文采取数值模拟和实验相结合的方法,建立高速电磁阀的动态响应特性数值模型,通过实验验证模型的准确度。在准确性满足要求的前提下,用数值仿真代替后续实验,这样易于获取研究所需数据,提高效率。
2.1 数学模型
电磁场求解基于麦克斯韦微分方程组:安培环路定律、法拉第电磁感应定律、高斯电通定律、高斯磁通定律,采用有限元离散形式,将工程中的电磁场计算转变为矩阵求解,进而直接或间接解得各物理量[7],具体为
(1)
(2)
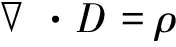
(3)

(4)
式中:H为磁场强度,J为传导电流密度,D为电通密度,t为时间,E为电场强度,B为磁感应强度,ρ为电荷体密度。电磁阀的机械运动方程为
(5)
式中:m为运动件质量,包括阀杆、衔铁和小弹簧等零件;x为衔铁位移;Fmag为电磁力;λ为考虑到流场影响的阻尼系数;k为弹簧刚度;F0为弹簧预紧力。
2.2 有限元模型
由于所研究电磁阀为非轴对称模型,为了保证计算精度,在Ansoft Maxwell中采取三维建模分析,并对模型进行了相应简化处理。因电磁阀的控制阀杆、衔铁复位弹簧、出油堵头、弹簧座、外壳、密封圈等为非软磁材料部件,其磁导率与空气相近,故建模时将其视为空气,包含于最后创建的求解域中[8]。由硅钢片叠压而成的电磁阀铁芯,根据实际外形尺寸建成一整体,在分配材料时,设置其属性为叠片,并给定叠压系数和叠压方向,建立的铁芯模型如图2(a)。由多匝铜导线绕制而成的励磁线圈,建模时将其等效为一个线圈环,同时做出环的一个纵截面作为激励输入端。加载激励时,指定线圈类型为绞线型,表示模型线圈环是由多匝线圈组成,并给定线圈匝数,建立的线圈模型如图2(b)。保持衔铁和铁芯之间的初始工作气隙为0.25 mm,根据衔铁的实际尺寸和结构建立的模型如图2(c)。由于电磁阀衔铁外表面、阻尼孔内表面为曲面,而Ansoft Maxwell三维瞬态磁场计算时要求运动物体必须是具有真实边界的三维实体,其表面不能为曲面,而必须是可分割的平面,于是需建立一多边形柱体空气包包裹衔铁,另建立一运动区域包裹衔铁的所有行程以将静止物体与运动物体分开,最后创建以空气环境包围整个模型的求解域,完整模型如图2(d)所示。

(a) 铁芯模型 (b) 线圈模型

(c) 衔铁模型 (d) 完整模型
图3为模型一切面的网格剖分示意图,铁芯、线圈、空气包的内部最大网格尺寸为3 mm,衔铁、运动区域、求解域的内部最大网格尺寸分别为2 、1 、4 mm。

图3 模型切面网格剖分示意图
2.3 实验与计算结果对比
电控单体泵系统油泵试验台如图4,通过单体泵堵头上开的安装孔把Kistler电涡流升程传感器安装在合适的位置(图5所示),升程传感器将控制阀杆位移转化为电压信号输出,并同时测量电磁阀线圈电流,即可得到高速电磁阀动态响应特性情况。

图4 电控单体泵系统油泵试验台

(a) 完整堵头与开安装孔堵头

(b) 传感器与堵头 (c) 传感器堵头的安装
将典型工况下(不同凸轮轴转速和喷油脉宽)实测电流数据分别导入Ansoft Maxwell软件作为激励进行仿真计算。表1、图6分别是各响应时间和阀杆升程曲线仿真与试验的对比。由表1可知,高速电磁阀关闭响应时间最大误差为2%,且仿真计算值均略小于试验值,关闭过程的阀杆升程曲线仿真也超前试验(如图6),这主要是仿真计算忽略了漏磁以及电磁阀温升致使衔铁和阀芯材料磁导率降低等效应,导致计算电磁吸力大于实际电磁吸力,使得仿真计算关闭响应时间缩短,阀杆升程曲线超前;开启响应时间最大误差为8.7%,同样仿真计算值均略小于试验值,阀杆升程曲线仿真也超前试验,其主要是因为仿真计算用铁磁材料的初始磁化曲线来近似表示其磁化过程,未考虑其磁滞现象,致使开启响应时间缩短。而在工程计算中,由于软磁材料磁滞回线很窄,用材料的初始磁化曲线近似表示其磁化过程,通过与试验对比可知,这种近似带来的误差是可以接受的。因此,利用该模型能够为高速电磁阀动态响应特性预测模型的得出提供准确的数据。
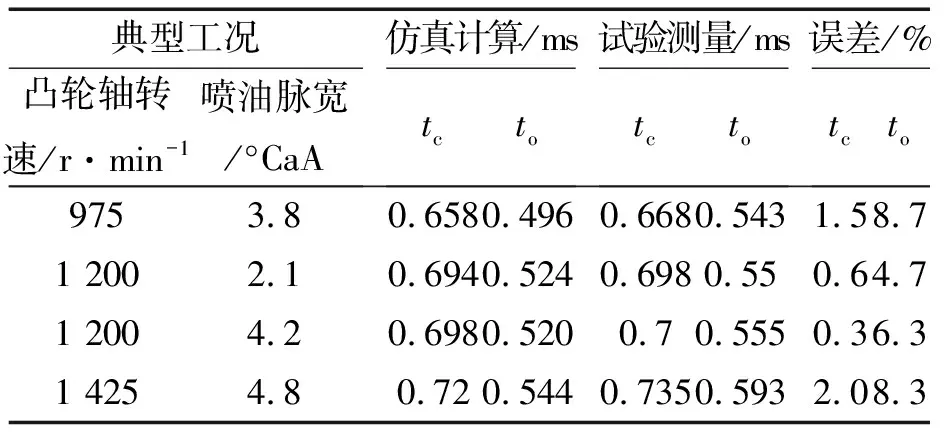
表1 响应时间仿真和试验的对比
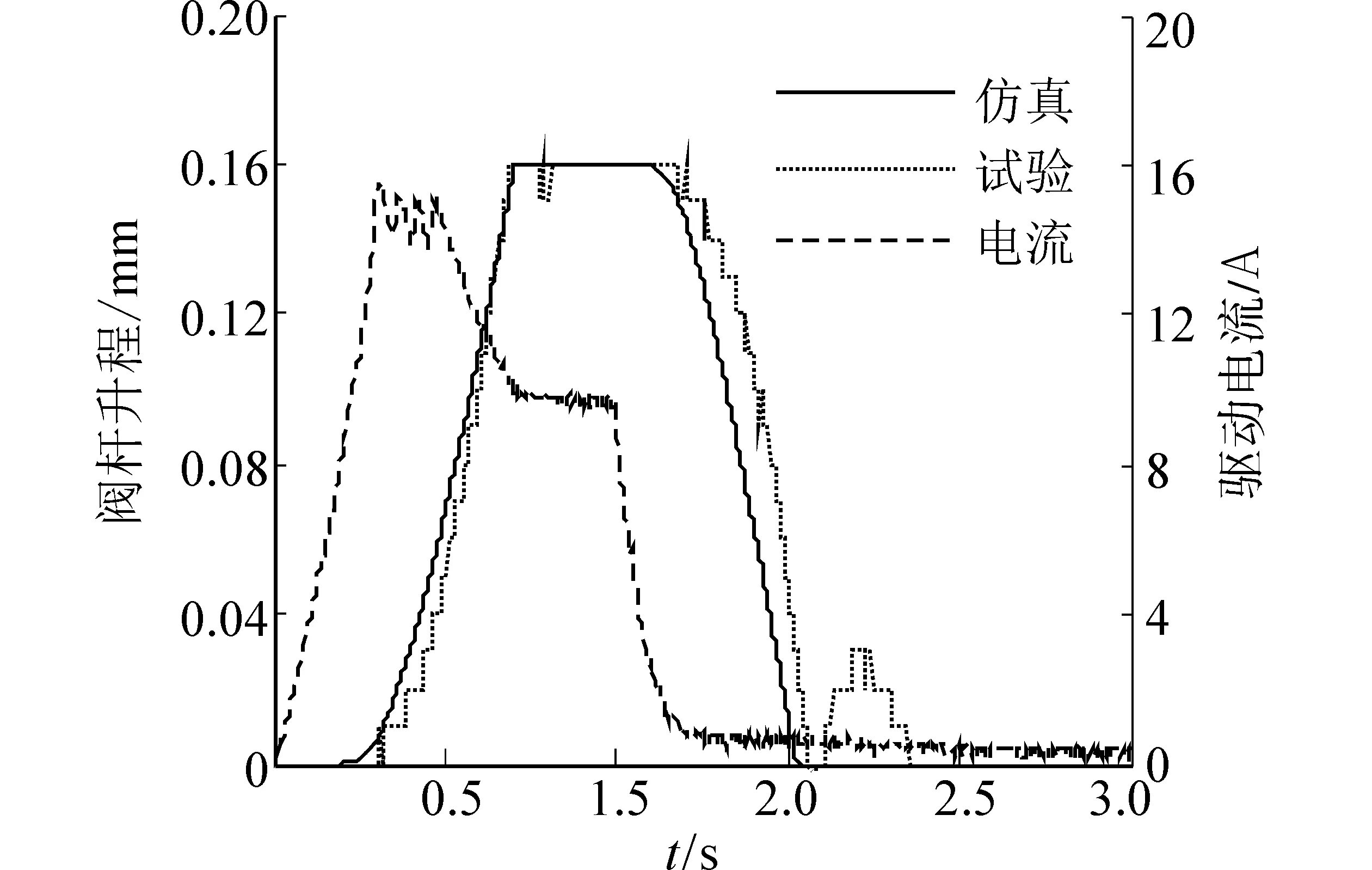
(a) 1 200 r/min,4.2 °CaA
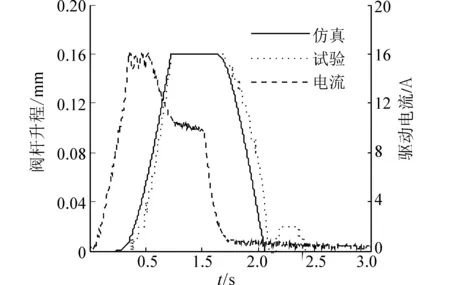
(b) 1 425 r/min,4.8°CaA
3 动态响应特性响应面预测模型建立
3.1 设计变量的选取
在电磁铁、衔铁结构参数和控制参数一定的情况下,由电磁阀的机械运动方程(式(5))可知,弹簧预紧力、运动件质量、阀杆升程等参数会对其动态响应特性产生影响,另外残余气隙也是其重要影响参数[9],因此本文针对这些参数进行高速电磁阀动态响应特性预测模型的建立。
3.2 响应面方法基本原理及建模
响应面方法最早由统计学家Box等提出,它是统计分析和实验设计方法相结合的产物,通常用于探究未知系统或过程的响应输出和影响因素之间的数学模型,应用系统的方式进行实验并取得所希望的响应值和因素水平,达到优化或预测响应变量目的,即通过合理的实验设计方法建立目标、约束与设计变量之间的近似函数[10]。响应面模型的建立如下。
通常假定参数或设计点是n维向量x∈Rn,与响应y存在如下关系为
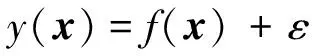
(6)
而真正的函数关系形式f是未知的,可能非常复杂,ε代表模型无法解释的其他来源的误差项。根据工程经验,通常应用上式的一阶或二阶Taylor展开式,作为相对小的区域内对真正函数的逼近形式。本文采用二阶模型,其能考虑模型曲性,且能拟合多种函数形式,所以常常能够逼近真实的响应曲面。二阶模型一般形式如下:
(7)
式中:φi(x)为基函数,k为基函数个数。
未知系数A=[α0α1…αk]T利用最小二乘法求取,即
可得
(8)
式中:Y为p(p>k)个实验点处的响应矢量,X为基函数矩阵:
(9)
3.3 实验设计
由式(8)可知,响应面模型的确定需要p个实验样本点及其响应值。而样本点的选取很大程度上决定了响应面的逼近精度,如何选择样本点,实验设计理论提供了指导思路。
中心复合设计(central composite design,CCD)是最为流行的二阶响应面实验设计方法,它将传统的插值节点分布方式与全因子或部分因子设计相结合,能以尽可能少的试验次数提供较多的信息,包括变量的效应以及试验误差。它的实验点由2n个析因设计或部分因子设计点(用于估计一阶项和交互作用项)、2n个轴向点或星点(用于估计二阶响应面模型纯平方项)和nc个中心点(提供一致精度和纯误差的估计)组成[11]。n为2的中心复合设计,如图7所示,中心点到因子高低水平的距离为±1(变量以规范化单位表示),轴向点或星点到中心点的距离为±α。
本文为4因素的中心复合实验设计,α取1,各因素的取值水平如表2所示,其中心复合实验设计示意图如图8。图8中每个立方体的3个坐标轴分别代表弹簧预紧力、运动件质量和残余气隙;坐标轴的箭头表示从变量的最小水平值到最大水平值;而从左到右的3个立方体则分别代表阀杆升程的最小水平值、中间水平值和最大水平值。中心点nc取3,最终设计了27个实验点(见表3)。
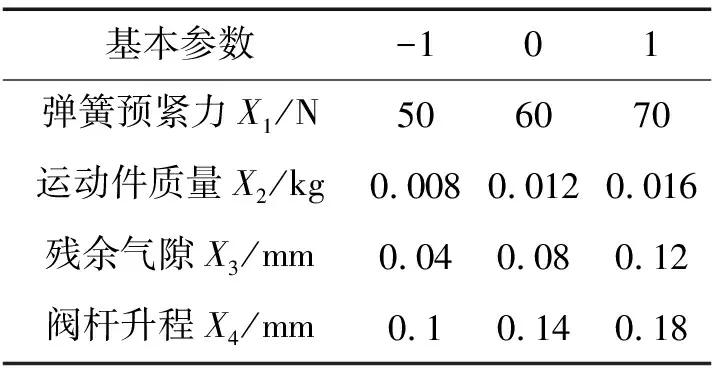
表2 实验设计因素水平

表3 实验设计表
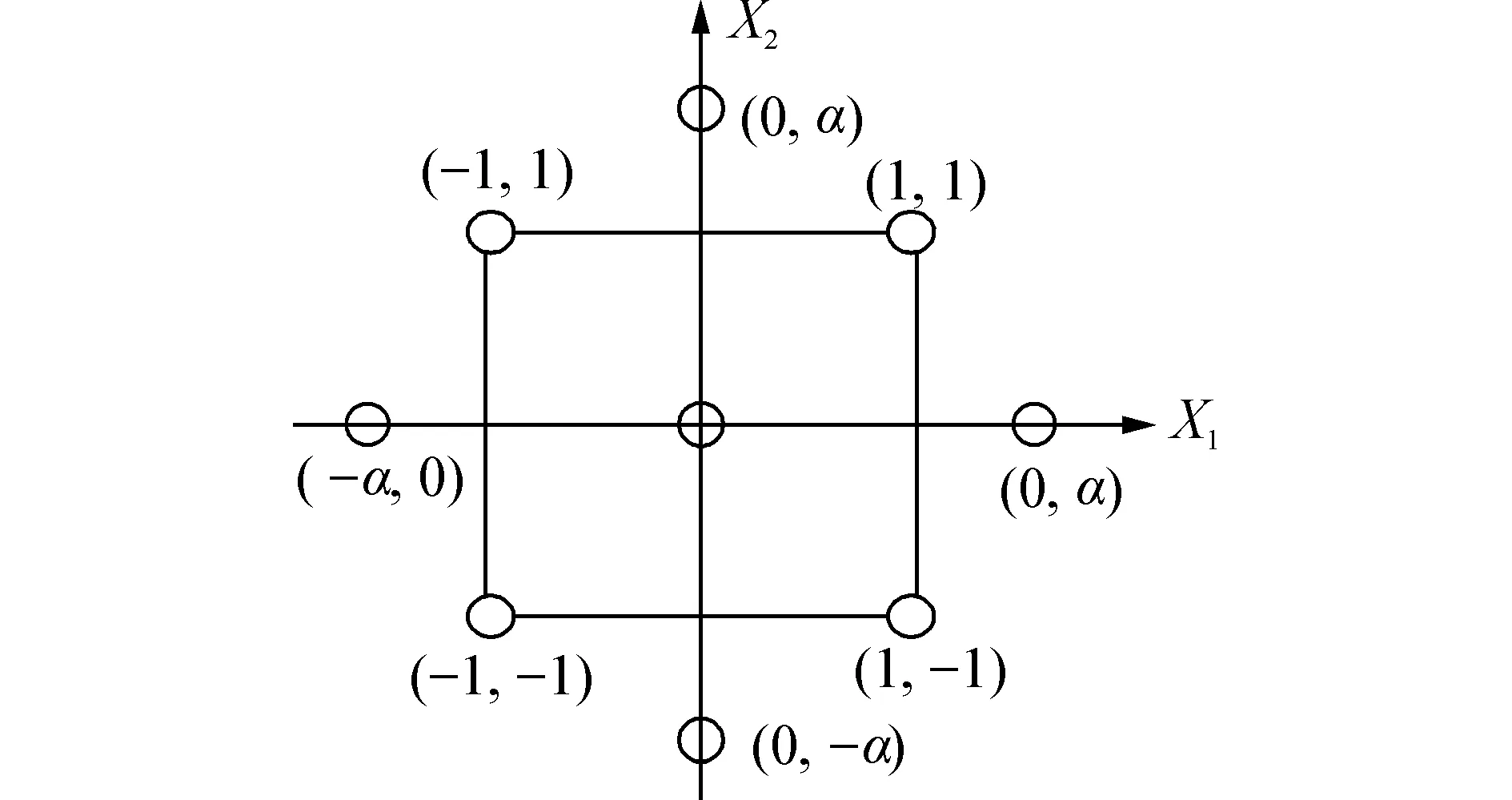
图7 两因素的中心复合设计
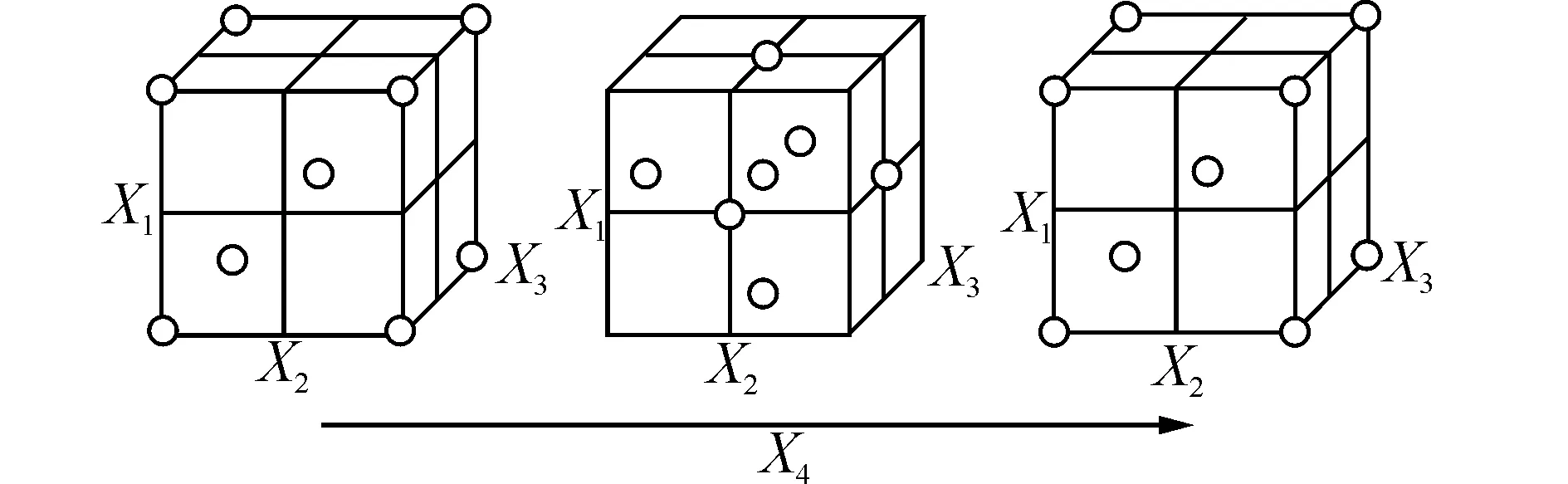
图8 四因素的中心复合设计
3.4 预测模型建立
以高速电磁阀的关闭响应时间tc、开启响应时间to作为模型的响应,利用Ansoft Maxwell中建立的高速电磁阀有限元模型按照实验设计表进行仿真实验进而得出响应值(如表3),通过式(8)进行回归分析,进而得出如式(7)所示的二次多项式的响应面模型。式(10)、(11)分别为高速电磁阀的关闭和开启响应时间的预测模型:
tc(X)=1.596 1-0.027 9X1-13.937 5X2-
6.678 5X3-6.797 2X4+0.000 1X12+
187.5X22+6.25X32+8.75X42+
0.131 3X1X2+0.071 9X1X3+0.093 1X1X4+
31.25X2X3+59.375X2X4+21.562 5X3X4
(10)
to(X)=0.764 3-0.013 3X1+10.317 7X2-
3.789 4X3+4.124 7X4+0.000 1X12-
76.388 9X22+11.111 1X32-0.763 9X42-
0.028 1X1X2+0.014 7X1X3-0.032 2X1X4-
8.593 8X2X3+11.718 8X2X4-0.078 1X3X4
(11)
4 预测模型的评价与验证
4.1 预测模型的评价
4.1.1 模型方差分析
由表4、5模型的方差分析可以看出,高速电磁阀关闭时间响应模型和开启响应时间模型F值均大于F0.05(14,2)=19.41,回归显著,且P值也都小于0.000 1,表明模型方程极显著。因此该回归模型与实际情况拟合良好。
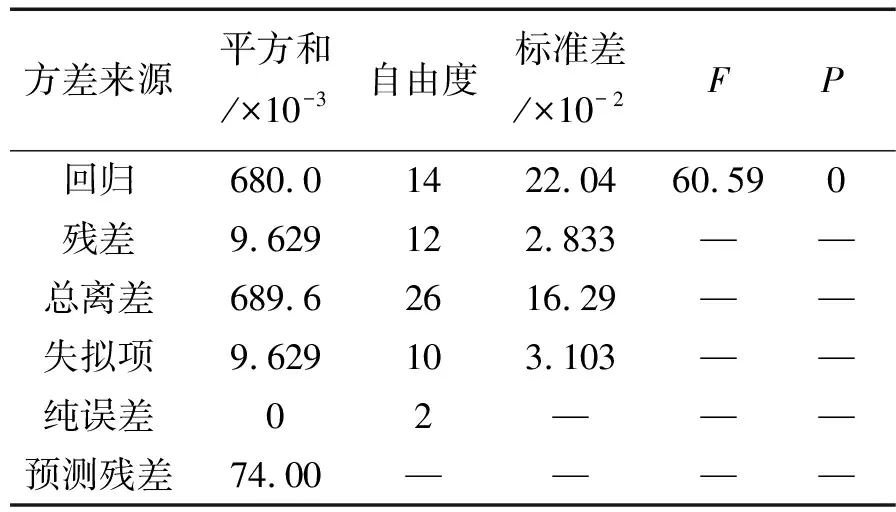
表4 高速电磁阀关闭响应时间回归模型的方差分析
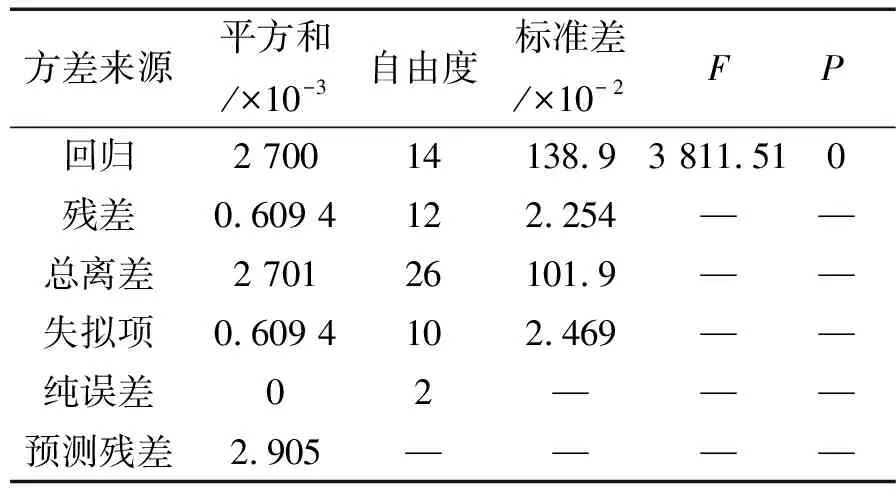
表5 高速电磁阀开启响应时间回归模型的方差分析
4.1.2 R2和Q2值评价
R2代表由回归模型所解释的实验结果的偏差百分比(R2=回归平方和/总离差平方和)表示回归模型与得出回归模型的实验结果之间的一致程度,它的取值在0~1之间,当R2>0.6时表示模型较好,且当R2>0.9时表示模型非常好;Q2代表由回归模型预测的实验结果的偏差百分比(Q2=(总离差平方和-预测残差平方和)/总离差平方和),表示回归模型的预测能力,取值在0~1之间。一般要求R2和Q2接近1最好,通常来说当R2>0.9,Q2>0.5,且两者的差不超过0.3时,就表示模型具有良好的一致性和预测能力,如果两者之间差值超过0.3,就表示模型不是很理想[12]。由图9可知关闭响应时间模型的R2值、Q2值分别为0.986、0.892 7,开启响应时间模型的R2值、Q2值分别为0.999 8、0.998 9,且两模型的R2值、Q2值之差均小于0.3,因此所建模型对实验结果具有好的一致性和预测能力。
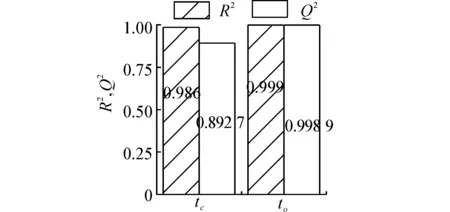
图9 各模型的R2、Q2
4.2 预测模型的验证
表6为各影响因素在各自给定取值范围内任意变化,实验设计模型预测结果与Ansoft Maxwell中仿真模型计算结果的对比。由表6可知,自变量参数取任意值时,实验设计数学模型预测所得关闭响应时间、开启响应时间和数值仿真计算结果对比,误差最大分别为5.1%、1.6%,说明了预测模型的精确性。
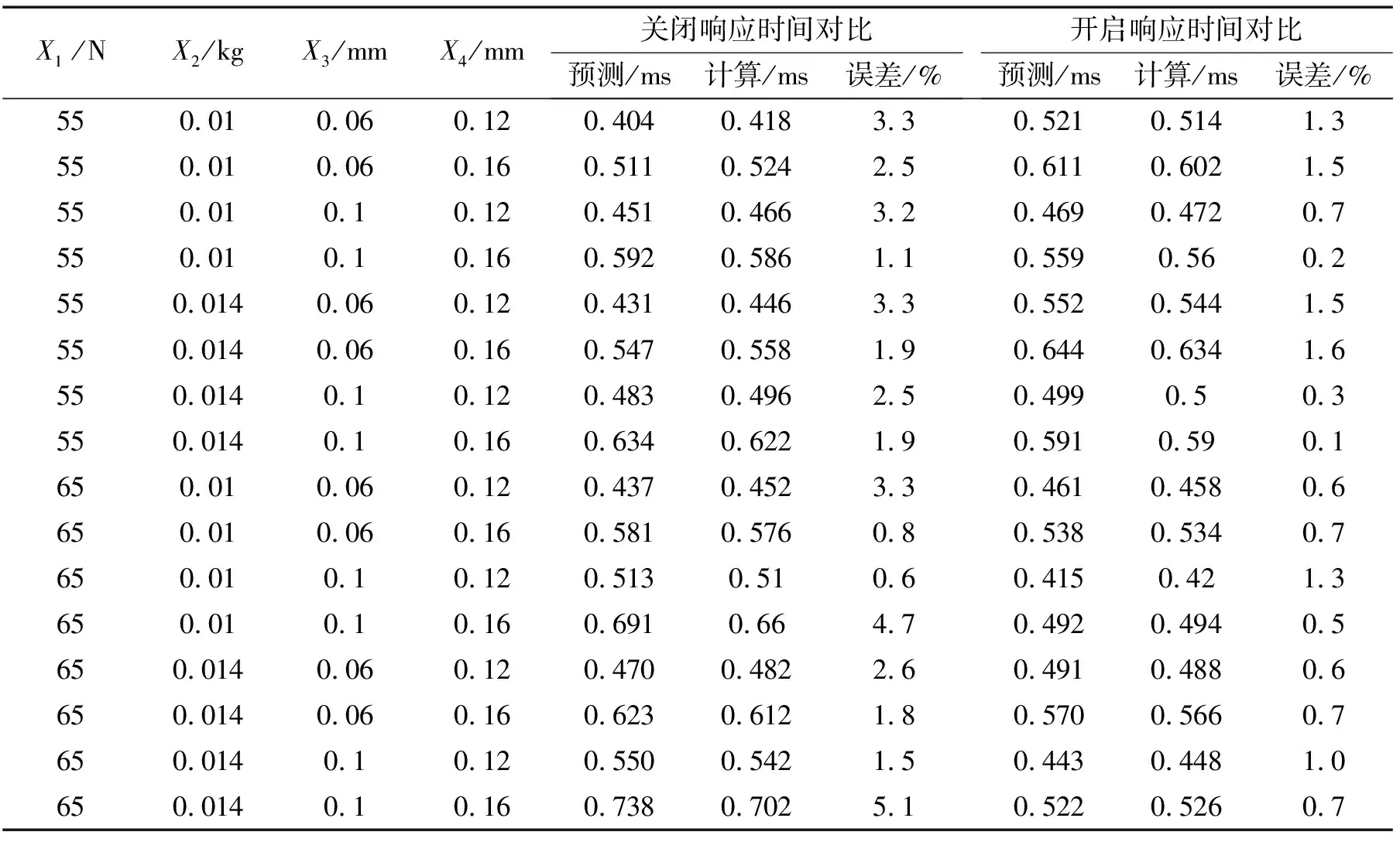
表6 预测与仿真计算结果的对比
综上,基于实验设计思想所得高速电磁阀动态响应特性关闭响应时间和开启响应时间预测模型具有良好的预测能力。
3 结论
1)Ansoft Maxwell环境中建立的电控单体泵高速电磁阀的三维有限元仿真模型具有良好的准确性,为高速电磁阀动态响应特性的研究提供了有效平台。
2)应用响应面方法,采用最小二乘法回归得出了高速电磁阀关闭响应时间和开启响应时间的预测模型。
3)高速电磁阀动态响应特性预测模型具有良好的准确性和预测能力,为其参数设计和匹配提供了有效工具。
参考文献:
[1]MULEMANE A, HAN J, SUBRAMANIYAM S, et al. Modeling dynamic behavior of diesel fuel injection systems[C]//2004 SAE World Congress. Detroit&Michigan, USA, 2004.
[2]仇滔,刘兴华,刘福水,等.电控单体泵燃油系统凸轮型线优化研究[J].内燃机学报,2008,26(5):476-479.
QIU Tao, LIU Xinghua, LIU Fushui, et al. The study for cam profile design of EUP[J]. Transactions of CSICE, 2008, 26(5):476-479.
[3]杨时威, 吴长水, 冒晓建, 等. 电控单体泵燃油喷射系统控制方法研究[J]. 内燃机工程, 2008, 29(3): 6-11.
YANG Shiwei, WU Changshui, MAO Xiaojian, et al. Research on the control strategy of fuel injection system with electronic unit pump[J]. Chinese Internal Combustion Engine Engineering, 2008, 29(3): 6-11.
[4]GREEVES G, TULLIS S, BARKER B. Advanced two-actuator EUI and emission reduction for heavy-duty diesel engines[C]//2003 SAE World Congress. Detroit&Michigan, USA, 2003.
[5]范立云,马修真,朱元宪,等.电控组合泵燃油温度动态特性研究[J].内燃机工程,2010,31(6):65-70.
FAN Liyun, MA Xiuzhen, ZHU Yunxian, et al. Investigation on dynamic characteristics of fuel temperature for electronic controlled assembly pump [J]. Chinese Internal Combustion Engine Engineering, 2010, 31(6): 65-70.
[6]FAN Liyun, Long Wuqiang, Zhu Yuanxian, et al. A characteristic study of electronic in-line pump system for diesel engines[C]//2008 SAE World Congress. Detroit, USA, 2008.
[7]刘慧娟, 傅为农. 薄壳单元法在接触物体间电磁力计算中的应用[J]. 电机与控制学报, 2012, 16(8): 101-106.
LIU Huijuan, FU Weinong. Computation of electromagnetic force on the interface using shell element method[J]. Electric Machines and Control, 2012, 16(8): 101-106.
[8]袁海军.基于Ansoft Maxwell仿真的电磁阀关闭过程动态特性研究[J].机电产品开发与创新,2011,24(5):82-84.
YUAN Haijun. Research of dynamic character of solenoid valve's closing process based on Ansoft Maxwell simulation [J]. Development and Innovation of Machinery and Electrical Products, 2011, 24(5):82-84.
[9]郝守刚,周明,夏胜枝,等.电控单体泵电磁阀动态响应特性数值仿真[J].内燃机工程,2003(2):10-13.
HAO Shougang, ZHOU Ming, XIA Shengzhi, et al. Numerical simulation of dynamic response characteristics of solenoid valve for electronically controlled unit-injection-pump[J]. Chinese Internal Combustion Engine Engineering, 2003(2):10-13.
[10]BOX G, WILSON K. On the experimental attainment of optimum conditions[J]. Journal of the Royal Statistical Society, 1951, 13(1):1-45.
[11]BOX G E P, HUNTER J S. Multi-factor experimental designs for exploring response surfaces[J]. The Annals of Mathematical Statistics, 1957, 28(1): 195-241.
[12]ERIKSSON L, JOHANSSON E, KETTANEH-WOLD N, et al. Multi and megavariate data analysis: part I: basic principles and applications[M]. Umea: MKS Umetrics AB, 2006: 58-61.

