全息数据外推与插值技术的极限学习机方法
孙超, 何元安, 商德江, 刘月婵
(1.哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001;2.哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001;3.船舶系统工程研究院,北京 100036)
近场声全息技术[1-4](near-field acoustic holography ,NAH)是一种研究噪声源识别和声场辐射问题的重要技术。通过测量声源表面附近的声场信息,逆向重建声源表面的各种声学量,进而重建声源外部三维声场。该技术用于水下结构振动的非接触探测和辐射噪声测量,声像清晰,噪声特性分析详尽,能够识别主要激励源,从而有效指导噪声控制方案。因此,该技术发展很快,并被应用于实际工程中。由于算法自身限制,通常要求全息测量孔径至少为声源尺寸2倍以上,以保证孔径边缘的声压得到足够的衰减,从而减小孔径有限性导致的误差。另外,对于大尺寸或结构复杂声源所产生的声场,测量时通常要布置较多测点,但需要大量的传感器和采集设备,使测量工作量大大增加,在一定程度上也限制了NAH技术的应用。近年来,局部近场声全息技术(patch NAH)的兴起在一定程度上突破了测量孔径的限制,可以在小孔径条件下实施NAH技术,从而为大尺寸声源重建提供了可能。全息数据外推就是一种典型的局部近场声全息技术,通过对较小测量孔径内的声压数据进行外推,获得了较大孔径内的声压数据近似值,间接地增大了测量孔径,从而减小了有限孔径效应对全息重建精度的影响。国内外都有相关学者对此问题已进行了较深入地研究,取得了较多成果[5-12]。
针对神经网络极限学习机算法(extreme learning machine,ELM)具有逼近非线性函数的能力,使其适用于解决信号处理过程中的分类辨识和回归拟合问题。本文将其与NAH技术相结合,提出了一种基于极限学习机的全息数据外推与插值技术。
1 极限学习机(ELM)理论
常规的神经网络主要有前馈、反馈和局部逼近神经网络。其中,单隐层前馈神经网络以其良好的学习性能在许多领域中得到了广泛应用。极限学习机ELM算法[13-15]是单隐层前馈神经网络的新算法,该算法随机产生输入层与隐含层之间的连接权值和隐含层神经元的阈值。在训练过程中,只需要设定隐含层神经元个数,便可获得唯一最优解。该方法与传统训练方法相比具有学习速度快、泛化性能好等优点。典型的单隐层前馈神经网络结构如图1所示。

图1 单隐层前馈神经网络结构
网络由输入层、隐含层和输出层组成,输入层与隐含层及隐含层与输出层间由神经元连接。设输入层有n个神经元,对应n个输入变量;隐含层有L个神经元;输出层有m个神经元,对应m个输出变量,设输入层与隐含层间的连接权值为w,隐含层与输出层间的连接权值为β,隐含层神经元阈值为b,则w、β、b可表示为
其中,wji为输入层第i个神经元与隐含层第j个神经元间的连接权值,βjk为隐含层第j个神经元与输出层第k个神经元间的连接权值。设隐含层神经元的激活函数为g(x),则网络输出为

(1)
式中:Q为训练集的样本数,wi=[wi1wi2…win],xj=[x1jx2j…xnj]T为训练样本,上式可表示为
(2)
H称为神经网络的隐含层输出矩阵,表达式为
(3)
在此基础上,由Huang等[20]提出的定理可知当激活函数g(x)无限可微时,单隐含层前馈神经网络的参数w和b在训练前可以随机选择,且在训练过程中保持不变。隐含层与输出层之间的连接权值β可以通过求解下面方程组获得

(4)
式中:h(x)为测试集的隐含层输出矩阵。Huang等给出当训练样本数远大于隐含层节点数时有:
(5)
否则
(6)

(7)
式中:K(u,v)为核函数,通常采用径向基核函数
(8)
对于参数C和γ,采用交叉验证方法寻找其最佳值,然后利用最佳参数训练模型。通过引入核函数,避免了选择隐含层神经元个数和定义隐含层的输出矩阵,进一步提高了ELM的学习速度和泛化能力。本文即采用这种基于核函数的ELM对全息数据外推和插值问题进行研究。
2 基于ELM的全息数据外推与插值
如图2所示,由测量区域S1中的测点声压外推区域S2-S1中的未测点声压,并保证预测值和尽可能接近真实值。将外推值与测量值组合获得更大全息孔径内的声场信息,相当于间接增大了全息测量面。这样,有效地减小了测量孔径,降低工作量,并提高了重建精度。

图2 全息数据外推示意图
概括起来,基于ELM的数据外推主要为以下步骤:1)选取测量区域S1中的坐标Xs、Ys和复声压作为训练样本集,其中坐标值为网络的输入值,而复声压的实部或虚部分别作为网络输出值,这样就构造出两类不同的网络并进行训练;2)根据需要外推的区域S2-S1确定位置坐标(Xpn,Ypn),n为预测的点数,同训练样本集中的坐标组成预测样本集中的输入值,输入至前面训练好的网络。网络的输出值为要预测的目标值,即扩展后的全息面S2上的声压实部和虚部,并保持初始全息面S1上的数据不变;3)根据外推后全息数据进行NAH计算,插值步骤与外推相似,插值区域为全息测量面S1测点间的插入点。
3 数值仿真
3.1 全息数据外推
首先验证该方法在解决全息数据外推问题的有效性。设平面内有2点声源,坐标分别为(0.2,0.2,0)和(-0.2,-0.2,0),两声源强度比为2∶1。测量面位于z=0.1 m,尺寸0.3 m×0.3 m(-0.15 m≤x≤0.15 m,-0.15 m≤y≤0.15 m), 测点间隔0.025 m,包含13×13个测点。外推面0.5 m×0.5 m(-0.25 m≤x≤0.25 m,-0.25 m≤y≤0.25 m)包含21×21个测点。分析频率为500、1 800、3 000 Hz。为了比较外推数据的准确性,定义外推误差公式:
(9)
式中:pt为各点理论复声压,Pa;pe为外推得到的全息面复声压,Pa。结果见图3。图中白色方框为初始全息测量孔径,由于全息面较小,测量孔径并未能完全覆盖声压峰值位置。通过外推方法,声场的辐射区域都被较好地恢复,外推结果与理论值基本一致。测量未得到的峰值区域得到了准确恢复,并且峰值和位置和理论值很相似。外推误差分别为7.91%、7.54%和12.43%。测量面的全息数据经外推后共441个测点,与实测点数相比增加1.6倍,说明本方法能够有效增大测量孔径的声场外推方法。

(a) 500 Hz理论声压

(b) 500 Hz外推声压

(c)1 800 Hz理论声压

(d) 1 800 Hz外推声压

(e) 3 000 Hz理论声压

(f) 3 000 Hz外推声压
接下来采用四周为无限大障板上的简支平板作为研究对象,平板在空气中受简谐力激励。选取参数如下:钢板长宽均为0.6 m,厚度为0.006 m,密度为7.8×103kg/m3,杨氏模量E=2.1×1011N/m2。选取板所在平面为z=0 m,全息面位置为z=0.06 m的平面。中心为坐标原点,激励点位置在(-0.05 m,-0.04 m),激励力幅值为5 N,频率分别为200、500、600、1 000 Hz。长宽方向的测量间隔均为0.025 m。全息面上S1的尺寸为-0.2 m≤x≤0.2 m,-0.2 m≤y≤0.2 m;扩展后的区域-0.3 m≤x≤0.3 m,-0.3 m≤y≤0.3 m。测量面S1共包含17×17个测点,扩展面S2共包含25×25个测点。计算过程中信噪比为30 dB,其中白色矩形框为S1中的仿真声压测量数据,采用ELM方法外推S2中的声压数据。测量面上复声压采用瑞利第一积分计算得出。另外,为分析本方法在较小测量孔径下声场外推精度,将全息测量孔径减少为0.3 m×0.3 m (-0.15 m≤x≤0.15 m,-0.15 m≤y≤0.15 m),测点间隔仍为0.025 m,扩展后的区域为0.6 m×0.6 m (-0.3 m≤x≤0.3 m,-0.3 m≤y≤0.3 m),即由13×13个测点外推25×25个测点。这里只给出600 Hz和1 kHz的仿真结果,见图4和图5,外推误差详见表1。
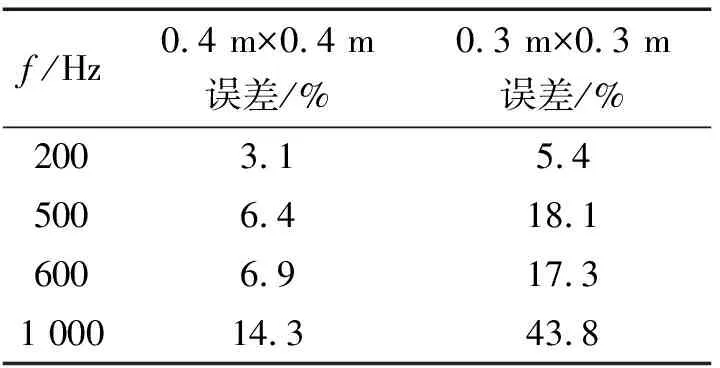
表1 不同全息孔径数据外推误差
能够看到,通过声场外推得到的声压分布峰值与理论值相比精度依然较高。不同频率全息面的声场外推结果与理论值吻合得较好。在较低频率时,外推精度较高;当频率变大时,声场分布变得复杂,精度有所下降。当输入的全息数据变少时,该方法的外推效果依然较好,全息数据经外推后与实际测点相比增加了456个测点。但高频时由于声场信息获取较少,外推精度有所下降。

(a) 600 Hz理论声压

(b) 600 Hz外推声压

(c)1 000 Hz理论声压

(d) 1 000 Hz外推声压

(a) 1 000 Hz测量声压幅值
3.2 采用外推数据重建声场
在前面平板辐射声场外推的基础上,基于外推数据采用统计最优近场声全息(SONAH)进行重建,并与基于初始测量值的重建效果和重建面的理论值相比较。全息面尺寸0.3 m×0.3 m,重建面位于z=0.02 m,大小0.6 m×0.6 m,其他参数不变。不同频率得到的重建误差见表2。
可以看到在不同频率时,采用基于初始测量值的重建声场和理论值相比误差较大,而采用基于ELM数据外推得到的全息面数据进行声场重建效果较好,重建精度提高很多。随着频率升高,误差逐渐变大,这是由于声场外推的精度随着频率的升高而下降造成的,但仍比外推前的效果要好,表明该方法是一种有效的Patch NAH技术。

表2 不同全息孔径数据外推误差
3.3 全息数据插值
仍采用单点激励无限大障板上的简支平板作为研究对象,测量参数和平板参数与上节相同。文中给出1 kHz时插值前后的声压幅值,见图5所示,表3给出不同频率时插值声压与理论声压的误差。为了比较方法的有效性及插值点个数对插值精度的影响,将全息面测点间隔设为0.05、0.1、0.15 m,插值后间隔0.025 m,即分别由13×13个、7×7个和5×5个的测点网格插值为25×25个虚拟网格。

表3 不同全息数据的插值精度
通过比较可知,基于ELM的插值方法在低频时精度较高,与理论声压相比误差很小;随着频率的升高,5×5个全息数据输入时将导致方法失效,这是由于频率升高,波长变小,单位波长内采集到的声场信息较少,而高频时声场更为复杂,需要更多的声场数据。当输入数据量增大时,插值精度显著提高,误差基本在10%以内,达到了预期效果。通过数值计算可知,该方法对于提高NAH采集效率进而提高NAH的重建精度是很有效的。
3.4 采用插值数据重建声场
采用上节7×7个测点,结合SONAH算法进行全息重建,并与采用插值后25×25个虚拟测点重建的结果进行对比。重建面位于z=0.02 m,其他参数不变。图6给出f=500 Hz情况下重建声压幅值对比。可以看出,插值后的全息面精度和重建图像的空间分辨率均明显提高,4个不同频率插值后的重建误差分别为4.05%、17.64%、23.9%和31.54%。

(a) 插值前重建面声压幅值

(b) 插值后重建面声压幅值

(c)重建面理论声压幅值
3.5 基于ELM的有限空间声场插值
基于ELM的声场插值技术除了可以将自由声场插值外,也可用于非自由声场插值。应用声学有限元软件ACTRAN对有限空间内声场进行仿真,有限元模型为边长1 m的立方体网格,如图7所示。

图7 非自由声场仿真
仿真过程中将其中一平面(图7中上表面)始终设置为水-空气界面,另外5个表面通过设置不同导纳使其满足阻抗边界、绝对软边界和绝对硬边界(反射系数分别为0.5、-1、1)。在立方体水域中声场由3个同相相干点源产生,点源位置分别为(0.1,0,0)、(-0.1,0,0)和(0.4,0,0),源强之比为1∶2∶1。全息面为半径为0.25 m的柱面测量面,长0.8 m,分析频率100~3 000 Hz。按照下面4种不同测点情况对不同边界条件声场进行插值:1)轴向间隔0.1 m,周向间隔18°;2)轴向间隔0.1 m,周向间隔36°;3)轴向间隔0.2 m,周向间隔18°;4)轴向间隔0.2 m,周向间隔36°。将每种测点均插值成为轴向间隔0.05 m,周向间隔18°的测量面,因此插值后每测量面有340个测点,将插值后的结果与理论值进行对比得到插值误差见图8所示。

(a) 阻抗边界

(b) 绝对软边界

(c)绝对硬边界
可以看到,在2 500 Hz以下不同边界的声场插值误差均小于6%,精度较高;随着频率的升高,误差逐渐变大,这是由于随着频率的升高,声波波长逐渐变小,在单位波长内的测点个数也逐渐变少,由于测点信息的不足导致了插值的精度有所下降。另外,从图中也能发现轴向插值倍数对插值精度的影响较大,误差随着轴向插值倍数的增加而变大,而周向插值倍数则影响较弱。当测量点个数为2)情况时,此时只有90个测点,通过插值得到了340个测点,且不同频率的误差都在5%以下。可见,通过声场插值可以大大节省工作量,提高了工作效率。

(a) 阻抗边界插值前声压幅值
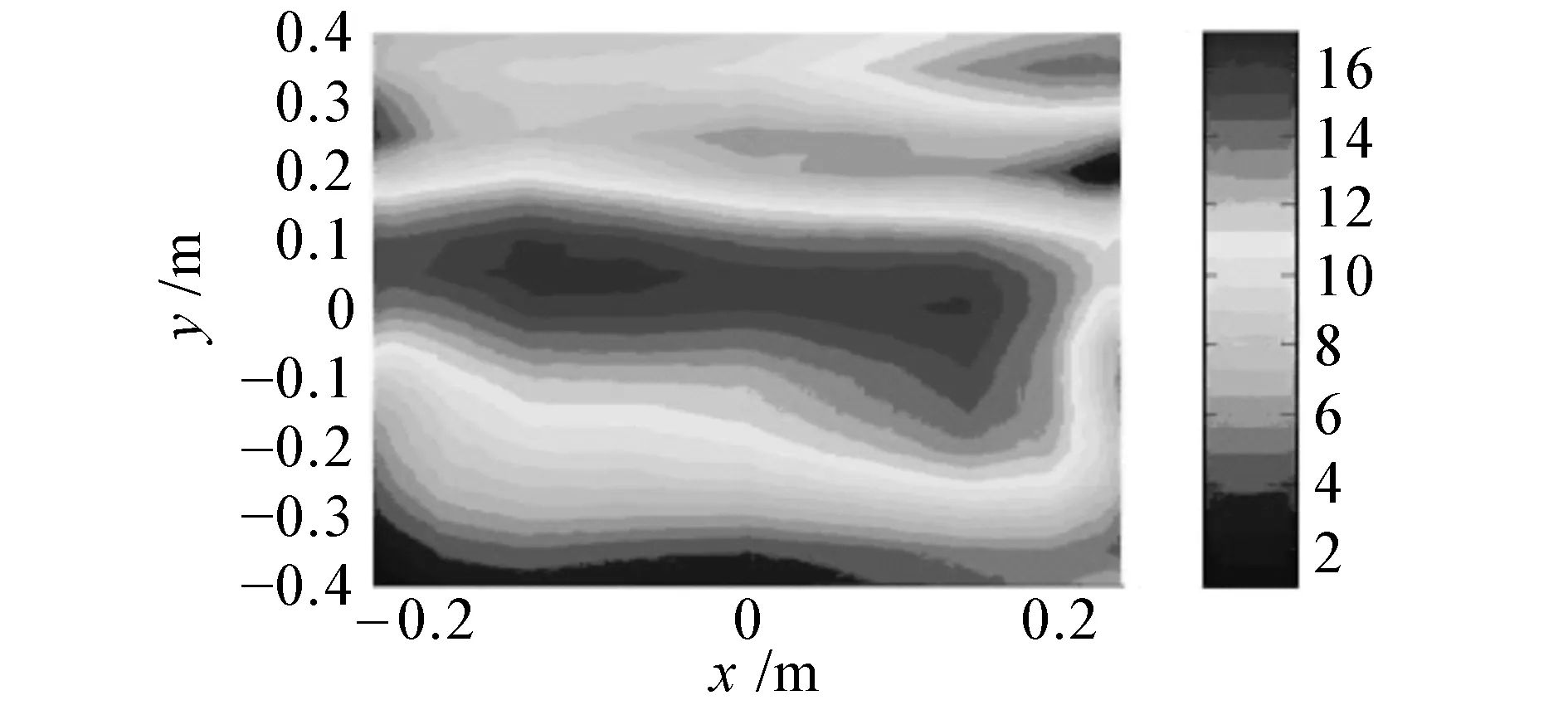
(b) 阻抗边界理论声压幅值

(c)阻抗边界插值后声压幅值

(d) 绝对硬边界插值前声压幅值

(e)绝对硬边界理论声压幅值

(f) 绝对硬边界插值后声压幅值
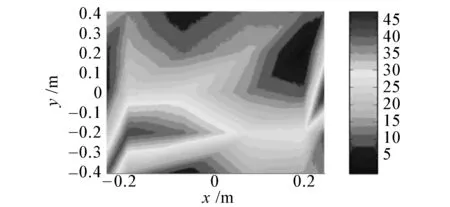
(g)绝对软边界插值前声压幅值

(h) 绝对软边界理论声压幅值

(i)绝对软边界插值后声压幅值
图9给出了频率在3 kHz时,测量点个数为条件4下的不同边界条件全息面测量声压和插值后的声压及声压理论值的对比图。可以明显看出,通过插值得到了由于测点间隔较大而遗漏的声场中的细节信息,从而有效提高了声场的空间分辨率。
4 结论
本文通过仿真对影响外推与插值结果的参数进行了分析,利用外推或插值后的全息数据进行全息重建。通过分析得出如下结论:
1) 采用ELM技术对小孔径测量面进行数据外推,有效地增大了测量面孔径。将外推得到的全息面数据进行NAH重建,能够有效提高声场重建精度,解决了测量孔径有限性造成的重建误差问题。
2) 在传感器个数较少时,采用ELM技术对全息数据进行插值,可以得到由于测点间隔较大而遗漏的声场中的细节信息,在不增加测点数量的情况下,提高了重建图像空间的分辨率,从而节省了工作量,提高工作效率。
3) 基于ELM的声场插值技术除了可以将自由空间声场进行插值外,还可应用于非自由声场环境中,对于不同边界条件插值效果均较好,验证了该算法的正确性与稳健性。
参考文献:
[1]WILLIAMS E G,MAYNARD J D,SKUDRZYK E. Sound reconstruction using a microphone array[J]. J Acoust Soc Am,1980,68(1):340-344.
[2]WILLIAMS E G,MAYNARD J D. Holographic imaging without wavelength resolution limit[J]. Phys Rev Letts,1980,45:554-557.
[3]何元安,何祚镛.基于平面声全息的全空间场变换:原理与算法[J]. 声学学报,2002,27(6): 507-512.
HE Yuanan,HE Zuoyong. Full spatial transformation of sound field based on planar acoustic holography:principle and algorithm[J]. Acta Acustica,2002,27(6): 507-512.
[4]何祚镛,何元安.近场声全息技术应用有关物理问题研究[J].声学学报,2007,32(2):137-143.
HE Zuoyong, HE Yuanan. The investigation on the physical acoustics problems of the NAH technique and its application[J].Acta Acustica,2007,32(2): 137-143.
[5]LEE M Y, BOLTON J S. Patch near-field acoustical holography in cylindrical geometry[J].J.Acoust Soc Am,2005,118(6):3721-3732.
[6]LEE M Y, BOLTON J S. A one-step patch near-field acoustical holography procedure[J].J Acoust Soc Am,2007,122(3):1662-1670.
[7]徐亮,毕传兴.基于波数域外推方法的近场声全息[J]. 机械工程学报,2007,56(5):2776-2783.
XU Liang,BI Chuangxing. Nearfield acoustic holography based on K-space data extrapolation method[J]. Chinese Journal of Mechanical Engineering ,2007,56(5):2776-2783.
[8]徐亮,毕传兴,陈剑.基于波叠加法的Patch近场声全息及其实验研究[J]. 物理学报,2007,37(9):1205-1213.
XU Liang, BI Chuangxing,CHEN Jian. Algorithm and experimental investigation of patch nearfield acoustic holography based on wave superposition approach[J]. Acta Physica Sinica, 2007,37(9):1205-1213.
[9]徐亮,毕传兴.全息声压场的加权范数外推方法[J].物理学报,2011,60(11):114304-2-10.
XU Liang, BI Chuangxing. Hologram pressure field weighted norm extrapolation method[J]. Acta Physica Sinica, 2007,37(9):1205-1213.
[10]杜向华,朱海潮,毛荣富.基于支持向量回归的patch 近场声全息研究[J]. 声学学报, 2012,37(3):286-293.
DU Xianghua,ZHU Haichao,MAO Rongfu.Patch near-field acoustic holography based on support vector regression[J]. Acta Acoustica,2012,37(3):286-293.
[11]张小正,毕传兴,徐亮.基于波叠加法的近场声全息空间分辨率增强方法[J]. 物理学报,2010,59(08):5564-5570.
ZHANG Xiaozheng,BI Chuanxing,XU Liang.Resolution enhancement of nearfield acoustic holography by the wave superposition approach[J]. Acta Physica Sinica, 2010,59(8):5564-5570.
[12]毛荣富,朱海潮.近场声全息中减少测量点数的研究[J].声学技术,2009,28(3):287-294.
MAO Rongfu, ZHU Haichao. A study of measurement point reduction in near-field acoustic holography[J].Technical Acoustics,2009,28(3):287-294.
[13]HUANG G B. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man and Cybernetics—Part B: Cybernetics, 2012,42(2),513-529.
[14]HUANG G B, SIEW, C K. Extreme learning machine with randomly assigned RBF kernels[J]. International Journal of Information Technology, 2005,11(1):16-24.
[15]HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006,70: 489-501.

