某扭转梁后悬架侧倾刚度的解算与优化*

赵 亮，晏海军，郭孔辉,2

(1.湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082；2.柳州孔辉汽车科技有限公司，广西 柳州 545000)

扭转梁式悬架是一种半独立悬架，整个后桥由扭转横梁和纵向摆臂焊接而成.当汽车曲线行驶时，悬架横梁产生扭转，起到增加悬架侧倾角刚度、减小车身倾角和提高汽车操纵稳定性的作用.

悬架的侧倾角刚度是影响汽车侧倾稳定性的主要因素之一[1]，直接影响到汽车操纵稳定性的一些性能指标，如不足转向度、中性转向侧向加速度.目前工程上对扭转梁的分析多采用生成扭转梁模态中性文件的方法进行分析,如文献[2-3]都是通过有限元软件建立模态中性文件对扭转梁悬架进行K&C分析；该方法是基于实际的物理结构,几乎没有进行优化的可能性,因此提出扭转梁悬架的侧倾角刚度的数值解析法.

本文根据扭转梁式后桥的结构特点，建立了悬架的侧倾力学模型，推导了带稳定杆扭转梁的扭转刚度等效在车轮处的侧倾角刚度的数学模型，并与虚拟样机ADAMS仿真的结果做了对比分析.在此基础上，进一步以扭转横梁和稳定杆截面尺寸参数为设计变量，采用改进的非支配排序遗传算法(NSGA-Ⅱ)对侧倾刚度及横梁质量进行了多目标优化，一次性获得pareto解集，通过选取合适的解，减少了悬架的非簧载质量，提高了悬架的侧倾角刚度，为补偿弹簧刚度的不足、提高整车平顺性、降低汽车的稳态振动频率、改善行驶特性提供了可能.对扭转梁后桥开发初级阶段总成特性参数的设计、选择具有深刻的理论指导意义，提高了扭转梁悬架的设计效率.

1 等效侧倾角刚度的计算

悬架侧倾角刚度是指汽车侧倾时(车轮保持在地面上)，单位车身转角下，悬架系统给车厢总的弹性恢复力偶矩[4].

1.1 悬架力学模型的建立

根据侧倾运动的实际行驶情况，当车轮位移较小即摆臂在小角度发生摆动时，与车身的连接衬套简化为球铰，后桥左右轮心处承受反向的垂向力，产生对横梁的扭矩，同时纵向摆臂与车体的铰接点处产生垂向支反力.结合扭转梁非独立悬架的具体结构可画出如图1所示的侧倾时的悬架受力图[5].

横梁的扭转力矩T由两对力偶产生，可以得到方程：

(1)

式中a为横梁轴线到车身连接球绞中心的纵向距离；b为横梁轴线到轮心的纵向距离.

扭矩T由横梁的扭转刚度k和两端面相对扭转角θ所得：

T=kθ

(2)

4个外力分别对悬架纵向对称轴线取矩,有力矩平衡便可得方程：

(3)

式中c为左右轮心的距离；d为左右球绞中心的距离.

图1 力学模型

1.2 扭转刚度计算

在杆件两端加上一对大小相等且反向的力矩M，如图2所示，设两端面的相对扭转角为θ，将扭转刚度定义：

(4)

横梁扭转刚度由两部分提供.一部分由V型截面梁，一部分由稳定杆.下面分别对两部分扭转刚度进行求解.

图2 带稳定杆的扭转梁示意图

1.2.1 V型截面梁扭转刚度计算

V型截面梁为非圆截面开口薄壁杆件，左右两端焊接在两纵摆臂上，因此横梁发生扭转时翘曲自由度受到了约束，因此只能通过约束扭转理论来计算横梁扭转刚度.运用约束扭转初参数解法求解之前，必须对约束扭转系数k进行求解[6].

(5)

折算弹性模量：

(6)

材料的剪变模量：

(7)

截面中线长度：

s=2(pr+L)

(8)

截面的自由扭转惯性矩：

(9)

式中l0为横梁长；r为截面中线圆弧部分半径；L为矩形部分长度；t为扭转梁厚度；p为圆弧所对应的弧度；G为材料剪切模量；E为材料弹性模量；μ为泊松比；E1为折算弹性模量；JW为截面主扇性惯性矩；Jd为截面自由扭转惯性矩.

下面用扇形面积法对JW进行求解.

由于是对称截面，截面与对称轴z相交于点M,将圆心o与M点分别设为参考扇性极点与参考扇性零点，如图3所示.将M0点沿截面中线顺时针旋转α角度到达M点,该点的参考扇性面积为：

w1=αr2,0≤α≤p

(10)

M点距z轴的距离为:

y1=rsinα

(11)

圆弧部分主扇性惯性矩为：

(12)

矩形与圆弧部分的交点c沿矩形中线方向移动长度b到c1点，该点的扇性面积为：

(13)

c1点距z轴的距离为:

y2=rsinp+bsinθ

(14)

矩形部分主扇性惯性矩为：

图3 主扇性极点求解示意图

(15)

整个截面的主扇性惯性矩为：

Jyw=2Jyw1+2Jyw2

(16)

整个截面对z轴的惯性矩：

(17)

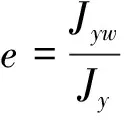
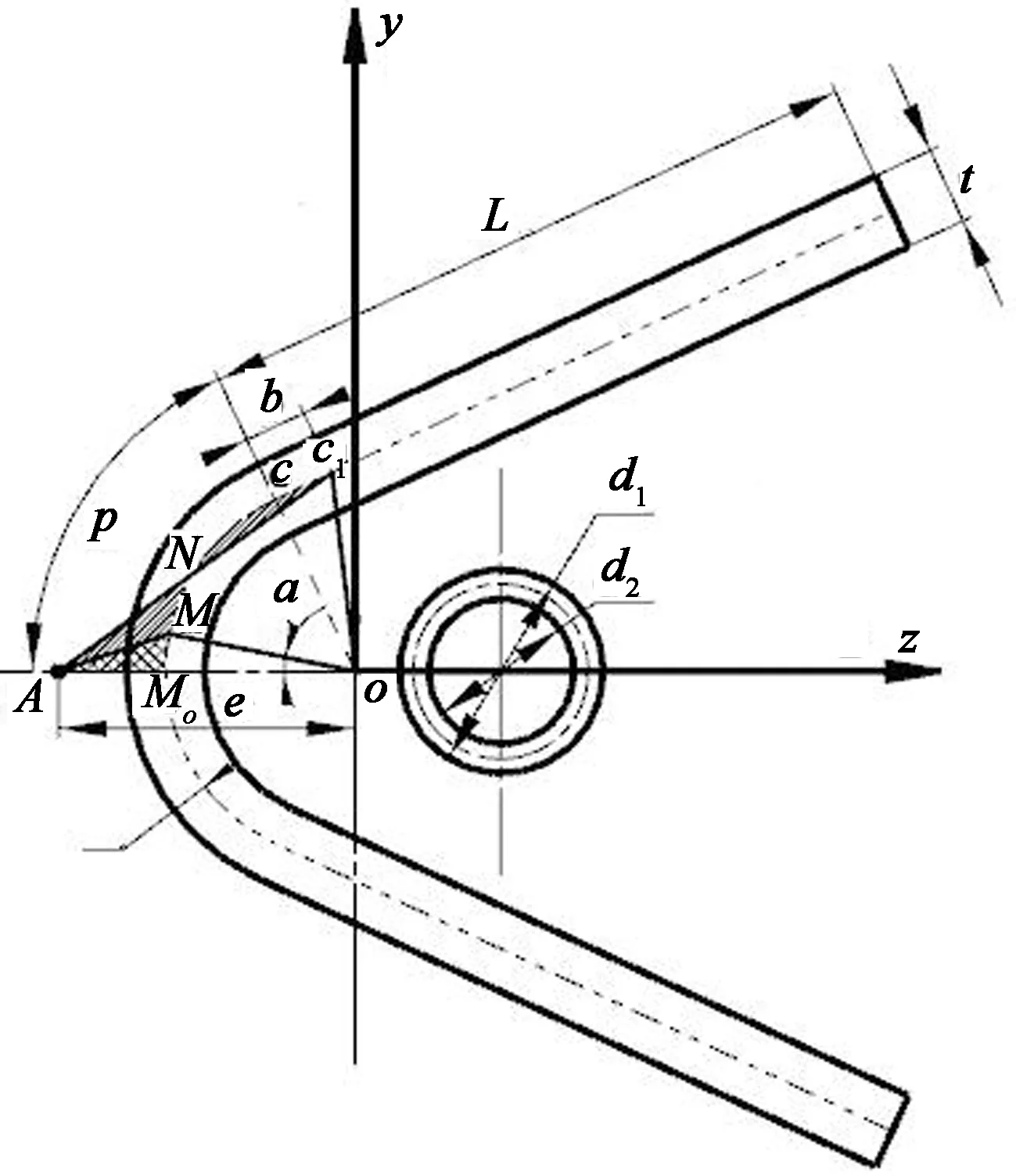
图4 主扇性惯性矩求解示意图

确定了主扇性的极点和零点，就可以得到M点的主扇性面积为：

(18)

则圆弧部分主扇性惯性矩为：

(19)

对矩形部分进行分析，c1点的主扇性面积为：

(20)

则2段的主扇性惯性矩为：

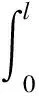
(21)

整个截面主扇性惯性矩为：

Jw=2Jwa+2Jwb

(22)

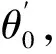
当x=l0时的边界条件有

根据约束扭转公式有：

根据第1，第2和第4个方程易解得

L0=M

在此便可以得到该薄壁横梁的扭转刚度:

(23)

1.2.2 扭杆扭转刚度计算

扭杆为圆截面闭口薄壁截面，在扭转载荷作用下不发生翘曲，其扭转刚度可以用自由扭转的公式计算：

(24)

整个扭转梁的扭转刚度为：

k=kl+kg

(25)

1.3 横梁扭转角

扭转梁悬架车轮的运动可以等效为以车身连接点o1与横梁对称面剪切中心(上文求得的主扇性极点)o2的连线矢量t为转轴摆动[7]，如图5所示.右轮心与右衬套硬点坐标见表1．

图5 等效运动学模型

表1 悬架硬点坐标

基于多体计算动力学欧拉四元素法[8]，定义：

纵向单位矢量p′=[1,0,0]T；

旋转轴的欧拉角矢量t=[tx,ty,tz]T；

欧拉四元素矢量：

q=[λ0,λ1,λ2,λ3]T=

T=

矢量p′绕摆轴转过β角得到矢量p=Tp′.

发生侧倾运动时如图6所示，横梁两端面的相对扭转角θ定义为[9]：

(26)

1.4 侧倾角刚度计算

根据定义，已知截面参数及悬架结构参数，由式(1)～(26)，设定轮跳范围(即对应的β的范围)，在每个分析步完成都有一个力矩和角度的变化，即可以求得侧倾角刚度CK:

式中B为轮距.

图6 横梁扭转角示意图

2 数学模型验证

考虑到衬套对扭转刚度的影响，将摆臂与车身用球铰链接，在有限元软件ABAQUS中建立了扭转梁式后悬架有限元仿真分析模型，如图7所示.

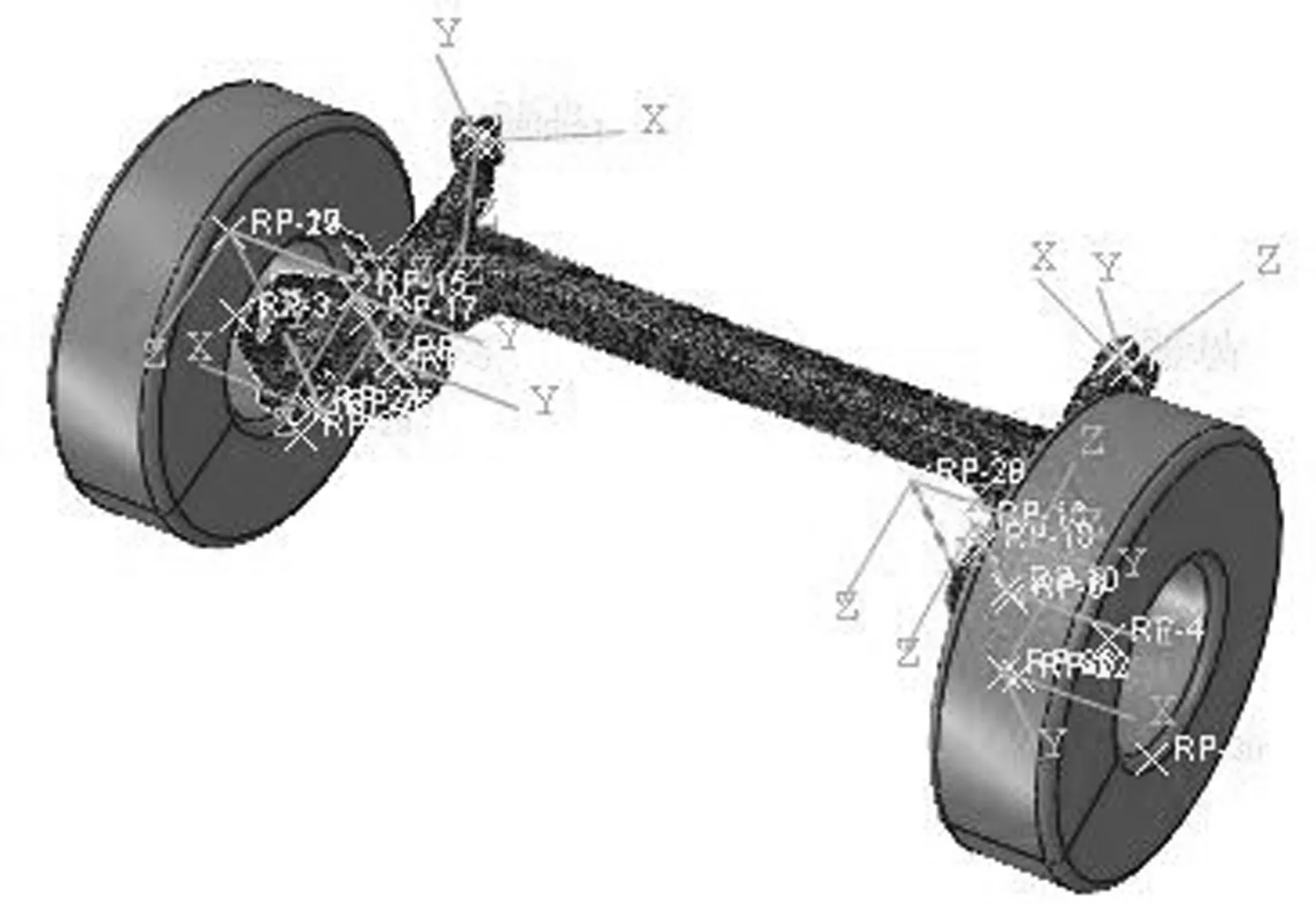
图7 ABAQUS有限元仿真模型

根据上文推导出的悬架侧倾刚度计算公式，在MATLAB中编写程序进行仿真，绘出悬架侧倾刚度随反向轮跳上下20 mm的变化曲线图，并将其与有限元仿真的数据作对比，结果如图8所示.

由图8可以看出ABAQUS悬架侧倾刚度曲线在小范围内随轮跳呈非线性变化，而理论模型侧倾角刚度呈线性变化，这是由于扭转梁悬架是一种半独立悬架，左右轮相互产生横向干涉，引起扭转角非线性变化，而理论模型完全等效成拖曳臂式独立悬架，故过程中扭转角随轮跳呈线性变化，所求得的曲线也呈线性变化.同时理论模型没有考虑到摆臂的弯曲及扭转刚度，这也导致理论值较仿真值要偏小的原因.总的来说，通过理论推导出来的侧倾刚度与ABAQUS仿真值比较接近，验证了该数学推导的正确性.

轮跳/mm

3 基于NSGA-Ⅱ算法多目标优化

NSGA-Ⅱ算法是一种基于快速分类的、采用精英策略的多目标遗传算法.首先,随机生成父代种群,然后对种群进行快速非胜出排序.根据每个非支配解的分级水平为指定适应值.进行选择、复制和变异操作生成具有N个个体的子代种群,父代和子代混合利用精英策略构造出新种群,并重复循环[10].

3.1 多目标优化模型的建立

考虑到该类悬架在横梁与纵臂焊接处往往会出现应力集中，需要通过加强板、拓扑优化等措施来改善其应力分布，而这对于数学求解应力带来了不便.

基于上述考虑，本文以横梁及扭杆的截面尺寸参数作为设计参数，其初始值与各变量范围见表2，建立以杆件的质量和侧倾刚度为目标函数的多目标优化数学模型如下:

s.t.xmin≤xi≤xmax

式中m为横梁的质量,m=2(pr+L)tl0ρ,ρ为材料密度；U为轮跳过程中的平均侧倾刚度；p，r，t，L，d2，d1分别代表设计变量x1，x2，x3，x4，x5，x6；l0为横梁长.

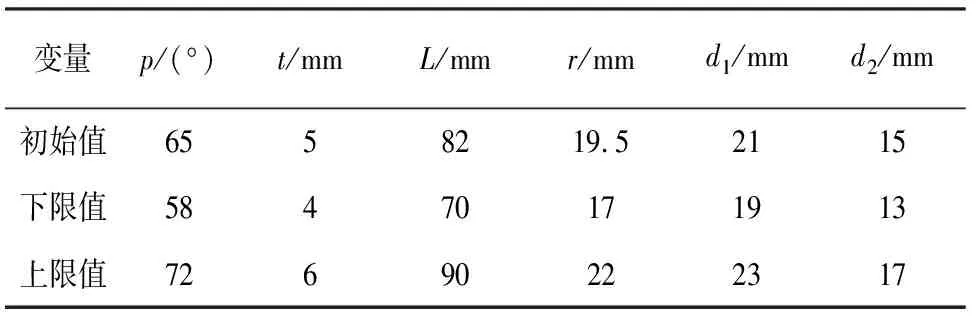
表2 截面尺寸设计参数

3.2 优化结果与分析

采用Matlab编写的NSGA-Ⅱ程序,应用上述数学模型,在悬架上下跳动20 mm的过程中,对两个目标函数进行优化.在种群规模为100,交叉概率为0.9,变异概率为0.1时,进行500代进化后得到该多目标优化的Pareto最优解集,如图9所示.

目标函数f1/kg

显然，从图9可以看出横梁的质量与平均侧倾刚度的倒数是一对矛盾体，往往不可能使得这两目标同时达到最优，只能在各目标之间进行协调权衡与折中处理，尽可能满足各目标达到最优.

为了使f1，f2尽可能最优，本文取A点.fn=(f1，f2)=(7.86,21.19)；响应的设计变量为：xn=(x1，x2，x3，x4，x5，x6)=(62.86，18.38，4，70，15.25，23).

对比优化前后目标函数的值，优化后带稳定杆的横梁总质量减少了10.95%，同时侧倾角刚度增加了10.77%，可以得出优化效果比较理想，为扭转梁开发提供了设计空间.

4 结 论

建立了带横向稳定杆的扭转梁截面参数与其等效在车轮处侧倾角刚度之间的数学模型，与虚拟样机ADAMS仿真的结果保持较高的一致性，验证了模型的正确性.基于该模型，采用改进的非支配排序遗传算法(NSGA-Ⅱ)对侧倾刚度和横梁的质量进行了多目标优化，获得pareto解，结果表明该优化方法是可行的.为补偿弹簧侧倾刚度的不足，提高整车平顺性能提供了可能[11].对扭转梁悬架设计初级阶段总成特性参数的设计、选择具有深刻的理论指导意义，提高了扭转梁悬架的设计效率.

[1]WINKLER C B,KARAMIHAS S M,BOGARD S E.Roll stability performance of heavy-vehicle suspensions[J].SAE Paper， 922426.

[2]CHOI B L,CHOI D H,MIN J,etal.Torsion beam axle system design with a multidisciplinary approach[J].International Journal of Automotive Technology,2009,10(1)：49-54.

[3]刘兴乾.扭转梁与四连杆悬架k&c特性分析及评价[D].长春：吉林大学汽车工程学院,2008.

LIU Xing-qian.The simulation analysis and evaluation for k&c characters of beam-twist and multi-link suspension[D].Changchun:College of Automotive Engineering,Jilin University,2008.(In Chinese)

[4]余志生,汽车理论[M].北京：机械工业出版社,2009:164-167.

YU Zhi-sheng.Theory of automobile[M].Beijing: China Machine Press,2009:164-167.(In Chinese)

[5]陈栋华,靳晓雄,黄海波,等.轿车扭杆式半独立后悬架动力学仿真和试验研究[J].汽车工程,2007,29(2):149-152.

CHEN Dong-hua,JIN Xiao-xiong,HUANG Hai-bo,etal.Dynamics simulation and experimental study on torsion bar rear suspension of passenger car[J].Automotive Engineering,2007,29(2):149-152.(In Chinese)

[6]包世华,周坚.薄壁杆件结构力学[M].北京:中国建筑工业出版社,1991:38-72.

BAO Shi-hua,ZHOU Jian.Structural mechanics of thin-walled bar[M].Beijing:China Architecture and Building Press,1991:38-72.(In Chinese)

[7]耶尔森·赖姆帕尔.汽车底盘基础[M].北京：科学普及出版社,1992:126,176.

YALE'S Lai Mparr.The automotive chassis engineering principles[M].Beijing:Popular Science Press,1992:126,176.(In Chinese)

[8]洪嘉振.计算多体系统动力学[M].北京：高等教育出版社,1999:37,49.

HONG Jia-zhen.Computational multibody system dynamics[M].Beijing: Higher Education Press,1999:37,49.(In Chinese)

[9]MUN K J,KIM T J,KIM Y S.Analysis of the roll properties of a tubular-type torsion beam suspension [J].Journal of Automobile Engineering,2010,224(1):1-13.

[10]DEB K，PRATA P A，AGARWAL S,etal.A fast and elitist multiobjective genetic algorithm: NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002(6):182-197.

[11]王望予.汽车设计[M].北京:机械工业出版社,2000:202- 205.

WANG Wang-yu.Automobile design[M].Beijing: China Machine Press,2000:202-205.(In Chinese)