高速∑-ΔDAC中插值滤波器的设计
张志龙,张长春,郭宇锋,刘蕾蕾,吉新村
(南京邮电大学电子科学与工程学院,江苏南京 210003)
射频识别(Radio Frequency Identification,RFID)是一种非接触式的自动识别技术。其中超高频(Ultra High Frequency,UHF)频段的应用最为广泛,它具有识别距离远、传送数据速度快、可靠性高等特点,被广泛地应用于物流管理、产品追踪、高速公路收费等领域[1-2]。
数模转换器(Digital to Analog Converter,DAC)是UHF RFID读写器发射链路中一个重要的组成部分,系统通过其产生模拟基带信号送至射频系统后进行调制、放大,最终通过天线发送出去。DAC按采样原理可分为两类:传统的奈奎斯特DAC和∑-ΔDAC。相比于传统型奈奎斯特DAC,∑-ΔDAC可以实现更高的分辨率、更易于集成,在高精度音频处理、视频、通信等领域正逐步取代传统型DAC并得到广泛的应用。
1 ∑-ΔDAC系统中的插值滤波器
terpolation Filter,IF)、噪声整形环路(Noise Shaping Loop,NSL)、低位DAC以及模拟低通滤波器(Low Pass Filter,LPF)。其中,IF实现过采样技术,NSL实现噪声整形技术,这是∑-ΔDAC主要采用的两种技术。IF在系统中的位置如图1所示。它主要作用是对高精度、低采样率的信号的进行升采样处理,并且滤除由于升采样造成的镜像信号,提高输出信号的信噪比以及过采样率。

图1 ∑-ΔDAC整体框图
插值滤波器一般由插值和滤波部分两部分组成,如图2a所示。插值部分主要作用是在相邻两个采样点中插入L-1个值并提高采样频率,插值的方法很多,最简单、最常用的是插零法,即在输入信号每相邻两个值x(n)和x(n-1)之间插入L-1个零值,这并不影响傅里叶变换,也就是插零后的信号频谱与原信号频谱一致[6],只是在频
∑-ΔDAC一般由四部分组成[3-5]:插值滤波器(In-带中产生了L-1个镜像。滤波部分一般由数字滤波器实现,其主要功能就是滤除前面插值部分产生的镜像。将采样频率从fs一次性升高到口OSR×fs,在理论上是可行的,但会导致整个电路都工作在最高的工作频率上,这不仅浪费了大量的功耗,而且占用了非常多的硬件资源。同时,由于低通滤波器要达到非常窄的通带和过渡带,这样就需要相当高的滤波器阶数,这样整个系统实现起来非常困难。因此通常采用多个滤波器级联[7],逐步提高采样频率的方法来实现。本设计采用的结构如图2b所示,在系统研究和理论分析的基础上,采用了三级级联的方式实现内插。从图中可以看出,插值滤波器的最前端为补偿滤波器用来补偿级联积分梳状(Cascaded Integrator-Comb,CIC)滤波器通带内的衰减,第二级为半带滤波器(Halfband Filter,HF)实现两倍的升采样,最后一级为CIC滤波器实现8倍的升采样,整个插值滤波器实现16倍升采样滤波功能。

图2 插值滤波器整体框图
2 插值滤波器的设计
本文根据ISO/IEC 18000-6C协议设计的插值滤波器,可用于UHF RFID发射机中。该插值滤波器采用三级级联结构,实现16倍插值,采样速率为3 MHz,最高工作频率为48 MHz,处理最大信号带宽为1.28 MHz。具体的设计方法为,首先确定设计指标,然后使用MATLAB对其进行系统级建模,并通过仿真对其系统级结构及参数进行优化,使得设计面积尽量减小,降低功耗,最后用Verilog HDL语言描述滤波器并对其进行仿真验证。
2.1 指标确定
本文设计的插值滤波器采样频率为3 M略高于奈奎斯特采样率,这样有两个好处:一是提高滤波器的过渡带带宽,降低了滤波器阶数;二是对于后面一级的滤波器的来说,其过渡带已足够宽,无需再用半带滤波器实现插值功能,而可以直接采用CIC滤波器从而减少硬件开销。由于后级的∑-Δ调制器采用的是5比特4阶的误差反馈型结构,为使性噪比达到70 dB以上,OSR必须大于8,由于OSR必须为2的幂指数,所以取16。数据传输速率和调制方式共同决定占用带宽。理论上,DBS-ASK、SSB-ASK和PR-ASK调制的最小信号带宽分别为传输速率的4倍、3倍和2倍[8]。UHF RHD从发射机到标签最大数据传输速率为128 kbit/s,调制后所得的最大基带信号带宽为512 kHz。从标签至发射机,最大传输速率为640 kbit/s,经调制后最大信号带宽不会超过1.28 MHz,所以确定滤波器的最大带宽为1.28 MHz。根据上述分析得到插值滤波器的主要设计指标如表1所示。

表1 插值滤波器的技术指标
2.2 补偿滤波器设计
由于CIC滤波器通带内存在较大的衰减,且半带滤波器通带内存在较小的波动,在级联以后,插值滤波器的通带衰减会变的很大,影响数据精度,因此需要设计一个补偿滤波器对通带内的频响进行补偿。补偿滤波器是一种典型的有限脉冲响应(Finite Impulse Response,FIR)滤波器,其系数为偶数个,并关于中心对称。补偿滤波器响应为反sine形状,刚好补偿了CIC滤波器sinc形状的响应。其系数比同阶半带滤波器多一倍的系数,本文对其系数进行了CSD编码[9]。为了降低系统的功耗要求,将补偿滤波器放在系统时钟最低的部分,即所有上采样滤波器之前。
2.3 半带滤波器设计
半带滤波器是一种特殊的FIR滤波器,具有通带截止频率和阻带起始频率关于0.5π对称,通带波动和阻带波动相等等特点。半带滤波器的中间系数为0.5,奇系数为0,这样相比于其它FIR滤波器就减少了一半的运算量,又由于其偶系数关于中心对称,可共用一个乘法单元,又减少了一半的运算量。用Matlab得到其系数,并对其系数进行CSD编码,即将乘法运算用移位相加来实现,减少了运算量,降低了硬件消耗。表2列出了第二级半带滤波器系数的CSD编码,其中第一位为符号位。本文对CSD编码略做改进,即得到滤波器系数的CSD编码后统一将其左移15位,这样减少总体的移位次数,也就是降低了运算量,最后将半带滤波器的结果统一右移15位,得到最终输出结果。
2.4 CIC滤波器设计
CIC滤波器[10]是一种结构十分简单的数字滤波器,只需加法器,运算速度快,在用作窄带低通滤波器时有着很高的计算效率。因此在多采样率系统中经常用在多级抽取、插值结构中的高频工作级中。CIC滤波器一般分为3个部分:梳状滤波器、插值器和积分器。对于插值滤波器,前半部分为梳状滤波器,中间为插值器,后半部分为积分器(可带延迟),而降采样滤波器刚好相反。N级传统CIC滤波器级联后的传递函数为
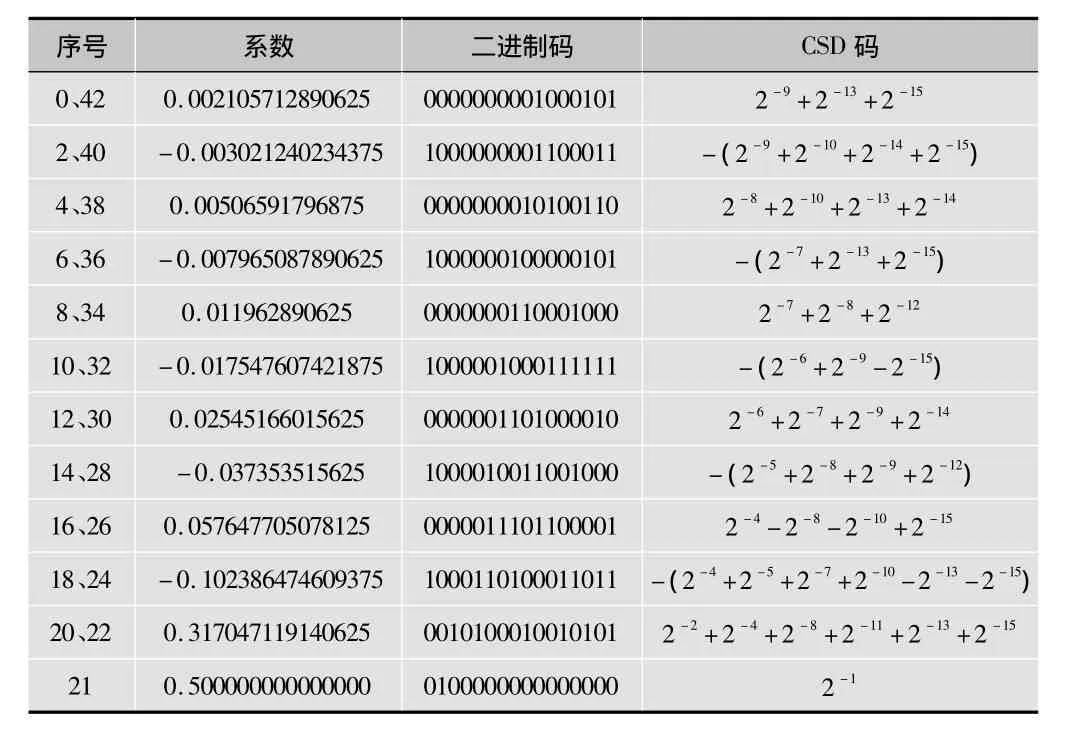
表2 半带滤波器系数的CSD编码

由式(1)可知CIC滤波器的性能由参数R,M和N共同确定,R是内插因子即CIC滤波器的升采样率;差分延迟M控制滤波器的频率响应,其决定插值后幅频特性曲线的零点位置,一般取1即可;级数N控制阻带衰减,加大N值可以加大阻带衰减和旁瓣抑制,减小通带混叠,但N越大通带内衰减就越大,所以N的值一般不超过5。
对于传统的CIC滤波器,以本参数为例,得到的CIC滤波器的结构如图3所示。从图中可以看出,积分部分为带有延迟的积分器,并工作在滤波器的最高频率上。该结构的主要特点是拥有很高的规则性并且不需要乘法器。但同时也可以看出,积分器是递归结构。为了避免积分器中的寄存器出现溢出,所以CIC滤波器的字长

式中:Bin是输入信号位宽,其他参数参考式(1)。当滤波器阶数或插值因子很高时,该结构的缺点将显现出来:积分器部分的内部字长会变得很大并且由于这部分工作在最高过采样频率下,所以功耗也会增大;另一问题是高的字长也会增加功耗。
为了解决上述字长效应和功耗大的问题,本文对CIC滤波器进行结构优化。对CIC滤波器传递函数进行约分,即消去分母部分得到的传递函数为

根据 Nobel恒等式[11],当多级系统包括线性系统,内插器和抽取器时,可以在处理信号的流程中重新排列几个部分的处理顺序,以便系统能够以更简单的方式实现。对于插值滤波器,则
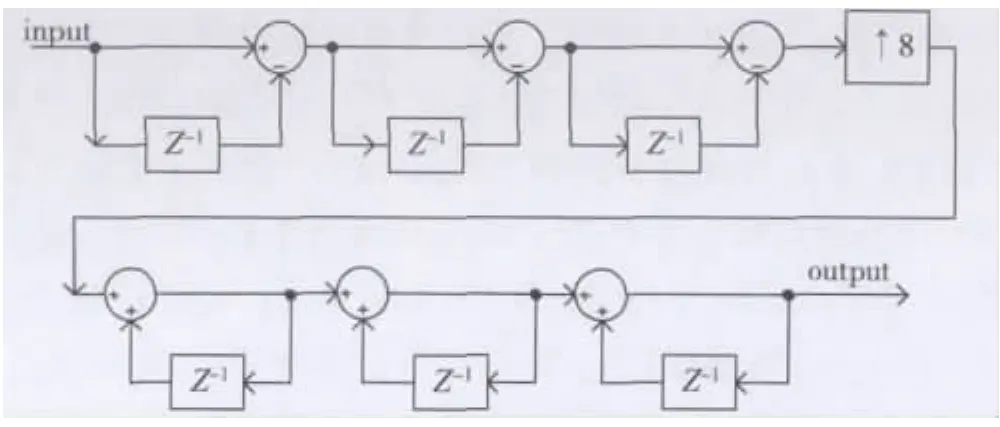
图3 传统CIC滤波器结构

图4给出了三级CIC滤波器分解过程,从图4c中可以看出,CIC滤波器的设计采用三级结构,实现8倍插值。每一级都由相同的低阶FIR滤波器构成,区别仅在于每一级滤波器的工作频率不同。该结构每一级位宽增加3位,共增加9位,与传统CIC滤波器位宽计算公式结果一致,解决了传统CIC滤波器需要考虑的位宽问题。这种高度规则的结构使结构设计和版图设计也变得更加容易。
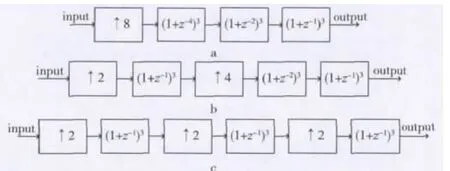
图4 三级CIC滤波器分解结构
3 仿真与验证
对于数字滤波器的系统仿真,主要是应用MATLAB中的Simulink仿真工具搭建插值滤波器系统,并在整个系统中对数字滤波器性能进行仿真验证。插值滤波器系统仿真如图5所示,其中输入的幅度为0.6 V,频率为0.5 MHz的正弦信号,采样率为3 MHz。图6为每个点的测试波形。通过对仿真波形进行分析可得出所设计的由补偿滤波器、半带滤波器和CIC构成的插值滤波器已经很好地完成了插值滤波的功能。
通过MATLAB产生10位量化0.25 MHz的正弦信号,采样频率为3 MHz。前仿真采用Modelsim软件,后仿使用VCS软件。图7所示为前后仿真对比,第一个波形为插值滤波器的输入信号,从图中可以清晰的看出,每个周期有12个采样点,没有满幅输入(满幅输入为1 023)是因为信号经过补偿滤波器补偿后输出会产生溢出;中间波形为插值滤波器最终输出,从图中可以看出插值后的波形很平滑,很好地实现了插值功能;最后一个波形是版图后仿的结果,使用VCS软件进行仿真,图中显示基本与前仿无多大差别。

图5 插值滤波器的simulink模型
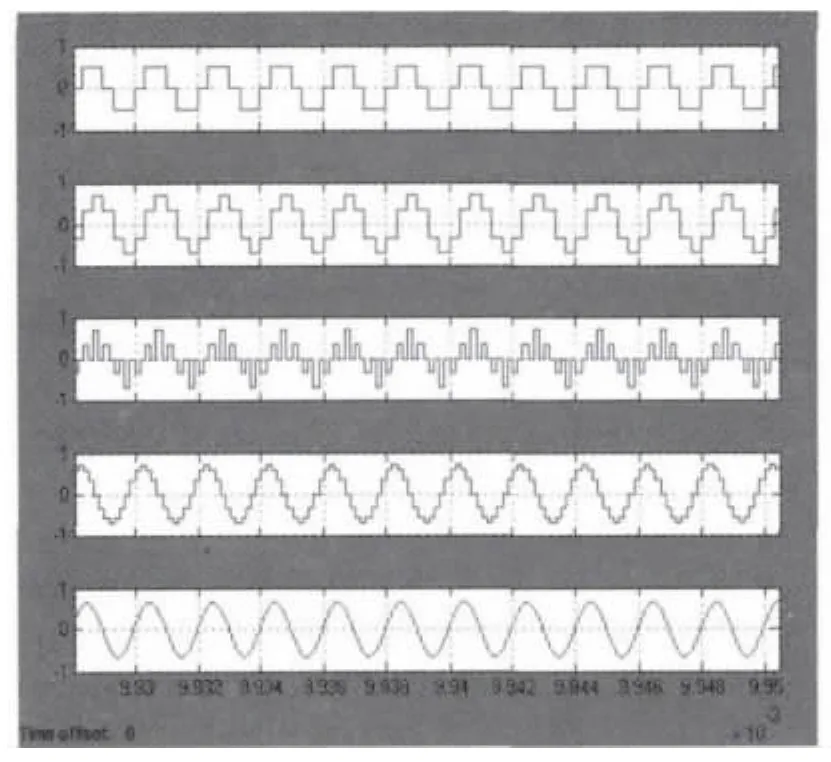
图6 插值滤波器的系统仿真波形(截图)

图7 前后仿真波形输出对比
整个插值滤波器的版图,核利用率达到0.68,芯片面积为720 μm ×720 μm,功耗约为5 mW,采用encounter软件自动布局布线。
4 小结
经过上述分析和仿真可以得出,本文设计的插值滤波器很好的实现了16倍插值滤波。补偿滤波器与半带滤波器的系数采用了CSD编码,降低了系统的复杂性和功耗,通过对CIC滤波器进行优化进一步降低电路功耗。基于标准0.18 μm CMOS工艺,实现了整个滤波器组,电路性能达到指标要求。

图8 版图(截图)
:
[1]刘宏伟,李成.ISO/IEC 18000-6C简析[J].信息技术与标准化,2007,7(7):17-20.
[2]ISO/IEC_CD 18000-6C,Information technology radio frequency identification for item management.part 6:parameters for air interface communications at 860 MHz to 930 MHz[S].2005.
[3]PARIKH V K,BALSARA P T,ELIEZER O E.All digital-quadraturemodulator based wideband wireless transmitters[J].IEEE Trans.Circuits and Systems,2009,56(11):2487-2497.
[4]QIU Dong,YI Ting,HONG Zhiliang.A low-power triple-mode sigmadelta DAC for reconfigurable(WCDMA/TD-SCDMA/GSM)transmitters[C]//Proc.Design Automation Conference(ASP-DAC),2011.Yokohama:IEEE Press,2011:119-120.
[5]邓玉清,唐宁.高精度音频∑-ΔDAC 的设计[J].电视技术,2011,35(7):56-58.
[6]金剑,唐宁.∑-ΔDAC中多级插值滤波器的研究与设计[J].电子器件,2009,32(5):916-919.
[7]CHEN Run,LIU Liyuan,LI Dongmei.A novel multi-stage interpolation filter design technique for high-resolutio∑-ΔDAC[J].Chinese Journal of Semiconductors,2007,28(11):1735-1741.
[8]陈梓敏,范国良.浅谈对《800/900MHz频段射频识别(RFID)技术应用规定(试行)》的理解[J].中国无线电,2007,8(13):31-33.
[9]FULLER A T G,NOWROUZ IAN B,ASHRAFZADEH F.Optimization of FIR digital filters over the canonical signed-digit coefficient space using genetic algorithms[J].Digital Signal Processing,1998,20(2):456-459.
[10]HOGENAUER E B.An economical class of digital filters for decimation and interpolation[J].IEEE Trans.Acoustics,Speech,and Signal Processing,1981,29(2):155-162.
[11]ZHOU Jinglei,LI Chengliang,QI Bo,et al.CIC interpolation filter design in the audio decoder[C]//Proc.International Conference on Computer and Communication Technologies in Agriculture Engineering.Chengdu:[s.n.],2010:141-144.

