Fe2TiAl热膨胀和弹性性质的第一性原理研究

路 庄，王少峰

(重庆大学结构与功能研究所，重庆 401331)

固体的热膨胀是指固体在有限温度下的体积增大行为，一般不改变固体的形状，由热平衡体积来描述。理论上，热平衡体积可以通过系统的自由能对于体积的极小值求得。研究固体的热膨胀是研究固体热力学性质的基础，基于此可以获得包括固体的热平衡体积、热膨胀系数、等温体模量、热容以及热弹性常数在内的一系列相关热力学参量，这就能有效地把材料的许多热力学参数从零温扩展到有限温度条件下，以便于更好地与实验进行对比和预测材料未知的热力学行为。

弹性是指固体材料在一定形变范围内可以恢复到原来状态的行为。固体的弹性性质一般由弹性常数来描述，它可以准确地确定固体中的应力-应变关系。理论上，弹性常数一般可以表示为系统的自由能对Lagrangian应变的二阶导数。弹性是固体的基本物理属性，对材料的弹性进行研究是对材料进行力学性质研究的基础。固体的很多基本固态性质都和弹性紧密相连，如原子间势、物态方程和声子谱等。此外，对弹性现象的研究还为研究固体的静力学和动力学行为搭建了桥梁。刻画弹性性质的参数还可以用来描述固体的比热、热膨胀、德拜温度、熔点以及格林爱森参数的热力学量［1］。

金属间化合物是指2种或2种以上的金属原子按一定规则排列所构成的化合物，一般分为2类:一类是具有低密度和良好的硬度、塑性、韧性以及抗高温蠕变性能的结构类金属间化合物;另一类是具有良好的光学、电学、声学、磁学性质的功能类金属间化合物。TiAl金属间化合物作为一种高温结构类金属间化合物，具有密度低、强度高、抗氧化性能好以及高温抗蠕变性能优异等性能，被广泛应用于航空航天以及汽车发动机领域，具有良好的工业应用前景［2-4］。尽管如此，TiAl金属间化合物在室温下脆性高、塑性差的特点却影响了其在工业上的广泛应用。围绕改善其脆性和塑性，国内外进行了广泛的研究，合金化就是其中的一种［4-7］。Fe2TiAl是通过在 TiAl金属间化合物中加入Fe元素来改善其室温塑性的典型材料，它除了具有TiAl金属间化合物所具有的所有优良性质外，还具有良好的室温塑性和韧性。目前对该材料的研究主要集中在Fe、Ti、Al之间的相互作用、成键性质和电子结构以及材料的磁性性质等方面［5，8-11］，而对其热膨胀和弹性性质，特别是对Fe2TiAl的塑性性质的研究还相对较少。

1 理论基础

准谐近似下晶体的自由能［12］为

式(1)中:第一项E(V)为基态能量，只与体积V有关;第二项为声子能量，其中T为温度，q为波矢，τ=1，2，…，3n，n 为单位原胞的原子数，ωτ(q)为声子频率，ωτ(q)和q之间的关系即为声子谱，可由式(2)［13-15］求出。

表示晶体中的格点A(AxAyAz)形变到格点B(BxByBz)，满足 AJ=B。Lagrangian应变定义为

其中I为单位矩阵。系统关于Lagrangian应变e的自由能F(e，T)可以在应变e=0附近展开为Taylor级数:

式(10)中:V0表示没有形变时晶格的体积。Lagrangian应变e也施加在V0的基础上。不难证明，Lagrangian应变张量e是一个对称张量，其在Voigt符号(xx→1，yy→2，zz→3，yz→4，xz→5，xy→6)下可以表示为

由此，可以把式(9)改写为

则式(12)可以进一步改写为

形变梯度矩阵可以通过反解式(8)获得:

形变后的基矢可以通过式(16)获得。

其中a表示未形变的基矢。

2 计算方法和结果

Fe2TiAl的晶体结构见图 1［4，18］。

图1 Fe2TiAl的晶体结构

不难看出，Fe2TiAl是属于面心立方的复式格子。定义平衡时次近邻Al原子间的间距为晶格常数a。显然，原胞的体积V=a3/4。单位原胞中的原子数n=4，原胞顶点处的8个Al原子共同构成了其面心结构的框架，在原胞长对角线的1/2处为一个Ti原子，分别在1/4和3/4处为2个Fe原子。

采用Vasp软件包来获取Fe2TiAl在实空间的力常数矩阵［19］。计算中采用一个2×2×2的超胞来模拟晶体中原子间的相互作用。平面波截断能选取为450 eV，倒空间的第一布里渊区在一个7×7 ×7 的 k 空间 Monkhorst-Pack［20］形式的格点上进行积分。采用Phonopy软件包来获取Fourier变换下的动力学矩阵，并获得Fe2TiAl的声子谱［21-23］。

从图2可以看出:Fe2TiAl的声子谱一共有12条。q=0时，ωτ(q)=0的声子谱有3条，称为声学波，代表了长波极限下原胞中原子的同向运动，即原胞质心的运动;q=0时，ωτ(q)≠0的声子谱有9条，称为光学波，代表了原胞中原子相对于质心的运动［15］。在Γ-X和Γ-L方向上，无论是光学波还是声学波，2支横波都是简并的;在XW-K-Γ方向上2支横波出现了分裂。声子频率在8～10 THz存在带隙，且声学波和光学波在声子频率在6～7 THz存在交叠。

Fe2TiAl的基态能量E(V)同样采用Vasp软件包［24-26］获得。在计算中，平面波截断能同样选取为450 eV，倒空间的第一布里渊区在一个15×15×15的k空间Monkhorst-Pack形式的格点上进行积分。声子的能量也由Phonopy软件包获得。笔者计算了18个体积点的自由能来获取Fe2TiAl在不同温度下的热平衡体积，且在0～1200 K，每隔2 K计算一次自由能。

图2 Fe2TiAl在高对称方向(Γ-XW-K-Γ-L)的声子谱

图3展示了Fe2TiAl热平衡体积的计算过程。可以看到:随着温度的增加，自由能等温线最小值位置对应的体积增大，表明晶体发生了热膨胀。

图3 不同温度下Fe2TiAl自由能F(V，T)随体积V的变化关系(自由能等温线间隔为100 K)

从图4、5可以看出:Fe2TiAl在温度小于50 K时的热膨胀并不明显。在温度小于200 K时，热膨胀系数与温度近似呈指数关系;在温度大于400 K时，热膨胀系数与温度近似为线性关系。

图4 Fe2TiAl的热平衡体积V(T)随温度T的变化关系

图5 Fe2TiAl热膨胀系数α(T)随温度T的变化关系

从图6可以看出:Fe2TiAl的等温体模量随着温度的升高而降低，表明温度越高，Fe2TiAl越容易被压缩。

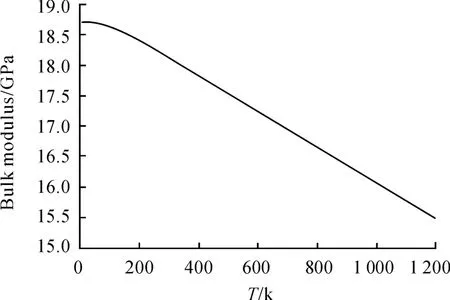
图6 Fe2TiAl等温体模量BT随温度T的变化关系

从图7可以看出:在温度小于200 K时，Fe2TiAl的等容热容和等压热容几乎无法分辨，且高温下Fe2TiAl的等容热容遵循能均分定理。

图7 Fe2TiAl等容热容CV和等压热容Cp随温度的变化关系

Fe2TiAl属立方晶系，其独立的弹性常数有3个(C11，C12，C44)。为了获得其完备的弹性常数，施加如下应变［27］:

对应的应变能密度分别为:

等温体模量可以表示为

要获得形变下的应变能密度，需要获得形变下的基态能量和形变下的声子能量。前者可以通过VASP软件包获得，但后者目前无法准确求出。大量实验结果表明:弹性常数随温度的变化主要来自体积膨胀，与温度关系不大［28-29］。基于此，温度为T时弹性常数就可以用该温度对应的热平衡体积V(T)来描述，即(T)=(V(T))。这样，就可以先计算出一系列体积V下的零温弹性常数，再根据热膨胀所获得的热平衡体积V(T)反解出T(V)，再把计算结果换为(T)即可获得弹性常数随温度的变化关系。由于基态能量已经考虑了声子能量对体积V的贡献，故可以用基态能量近似地代替零温自由能F(V)。不同体积V下的应变能密度就可以表示为

计算了应变ξ从-0.02到0.02间隔为0.002的21个应变能密度点，以此获取较为准确的应变能密度和应变之间的函数关系。对于立方晶系，等熵弹性常数和等温弹性常数之间有如下关系:

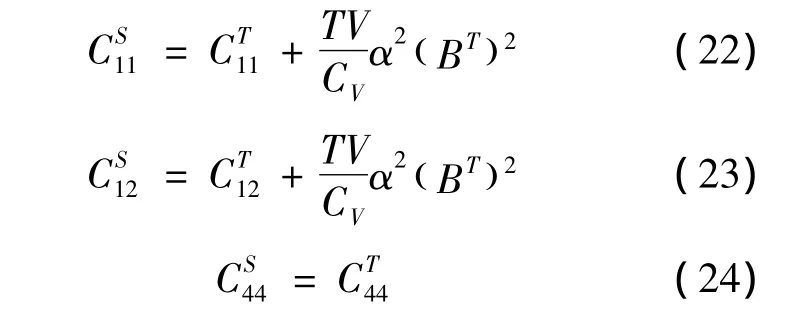
Caushy 压强［30］定义为

Caushy压强可以在一定程度上反映材料的塑性。通常塑性好的材料具有正的Caushy压强，且Caushy压强越大，材料的塑性越好;反之，材料的塑性越差。

从图8可以看出:Fe2TiAl的Caushy压强为正值，表明其具有较好的塑性;随着温度的升高，材料的Caushy压强逐渐减小，表明材料的塑性随温度的升高变差。

图8 Fe2TiAl的等熵弹性常数以及Caushy压强随温度的变化关系

最后，将计算结果与之前的计算结果及实验值作比较，如表1所示。

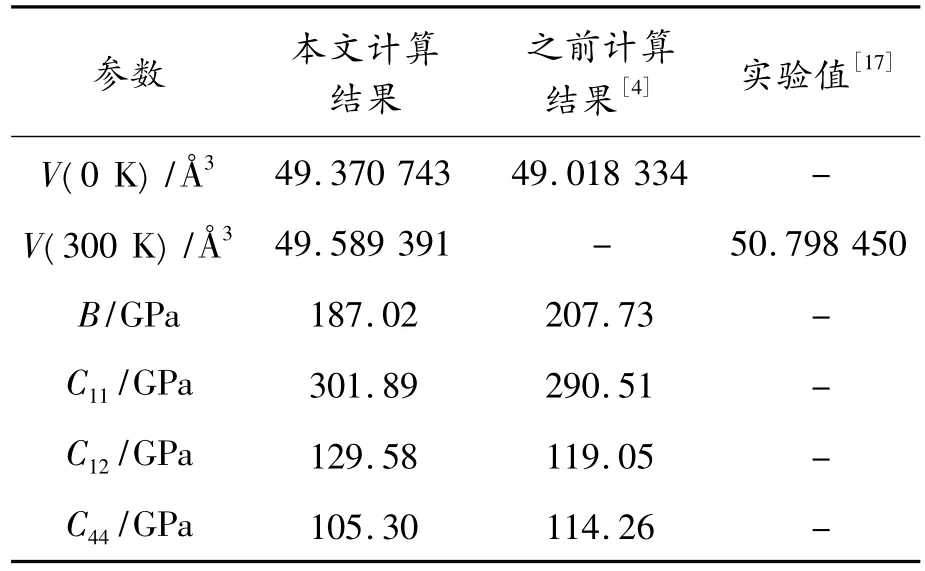
表1 Fe2TiAl的零温平衡体积V(0 K)、室温平衡体积V(300 K)、零温体模量B和零温弹性常数CIJ

3 结论

1)基于晶格动力学理论，获得了Fe2TiAl的声子谱共12条，包括3条声学支和9条光学支。

2)基于密度泛函理论和准谐近似求得了Fe2TiAl的热平衡体积，并在此基础上获得了Fe2TiAl的热膨胀系数、等温体模量、等容热容以及等压热容。

3)基于弹性理论，计算了Fe2TiAl的等熵弹性常数，并获得了Fe2TiAl的Caushy压强随温度的变化关系，得出了Fe2TiAl的塑性随温度升高而变差的结论。

4)将本文的计算结果与之前的计算结果及实验值作了对比，发现本文计算的零温平衡体积与之前的计算结果吻合较好，室温平衡体积接近实验值，但零温体模量和零温弹性常数与之前的计算结果有一定差距。

［1］Wallace D C，Seitz F，Turnbull D.Solid State Physics［M］.New York:Academic，1970.

［2］杨帆，田楠，王帆，等.基于TiAl多孔载体的钙钛矿型催化剂的汽车尾气催化性能［J］.功能材料，2013(18):2616-2619.

［3］林涛，刘小婷，邵慧萍，等.高Nb-TiAl合金凝胶注模成形的制备研究［J］.功能材料，2013(22):3359-3362.

［4］刘显坤，刘颖.Fe2TiAl结构和热力学性质的第一原理计算［J］.稀有金属材料与工程，2012，41(S2):479-483.

［5］陈玉勇，张树志，孔凡涛，等.新型β-γTiAl合金的研究进展［J］.稀有金属，2012(1):154-160.

［6］何鹏，李海新，林铁松，等.TiAl合金与镍基高温合金的扩散连接［J］.焊接学报，2012(1):591.

［7］孔凡涛，陈子勇，田竞，等.提高TiAl基合金室温塑性的方法［J］.稀有金属材料与工程，2003(2):81-86.

［8］Webster P J，Ziebeck K R A.Chem Solide［J］.Philosophical Magazine B，1973，34:1647.

［9］刘显坤，刘颖.Fe_2TiAl结构和热力学性质的第一原理计算［J］.稀有金属材料与工程，2012(S2):479-483.

［10］刘显坤，刘聪，郑洲，等.First-principles investigation on the structural and elastic properties of cubic-Fe_2 TiAl under high pressures［J］.Chinese Physics B，2013(8):561-566.

［11］Mohn P，Blaha P，Schwarz K，et al.Magn Mater［J］.Journal of Magnetism and Magnetic Materials，1995，140-144:1825-1828.

［12］Wang R，Wang S，Wu X，et al.First-principles phonon calculations of thermodynamic properties for ductile rareearth intermetallic compounds［J］.Intermetallics，2011，19(10):1599-1604.

［13］黄昆原，韩汝琦.固体物理［M］.北京:高等教育出版社，1988.

［14］韩述斌.固体物理效应与现代传感器技术［J］.压电与声光，1997(4):20-23.

［15］李正中.固体理论［M］.北京:高等教育出版社，2001.

［16］汪志诚.热力学与统计物理［M］.北京:高等教育出版社，2008.

［17］Brugger K.Thermodynamic Definition of Higher Order E-lastic Coefficients［J］.Phys Rev，1964，133:A1611.

［18］Blanco M A，Francisco E，Luana V.Comput Phys Commun［Z］.

［19］Kresse G，Marsman M.VASP guide［EB/OL］.［2013-12-21］.http://cms.mpi.univ-ie.ac.at/vasp.

［20］Monkhorst H J，Pack J D.Special points for Brillouinzone integrations ［J］.Phys Rev B，1986，13:5188-5192.

［21］Togo A，Chaput L，Tanaka I.First-principles phonon calculations of thermal expansion in Ti3SiC2，Ti3AlC2，and Ti3GeC2［J］.Phys Rev B，2010，81:174301-174305.

［22］Togo A，Oba F，Tanaka I.Defect energetics in ZnO:A hybrid Hartree-Fock density functional study［J］.Phys Rev B，2008，78:134106-134111.

［23］Togo A.Phonopy［EB/OL］.［2013-10-18］.http://phonopy.sourceforge.net/.

［24］Kresse G，Hafner J.Ab initio molecular dynamics for open-shell transition metals［J］.Phys Rev B，1993，48:13115-13118.

［25］Kresse G，Furthmüller J.Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set［J］.Comput Mater Sci，1996，6:15-50.

［26］Kresse G，Furthmüller J.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set［J］.Phys Rev B，1996，54:11169-11186.

［27］Wang R，Wang S，Yao Y，et al.The temperature-dependent elastic properties of B2-MgRE intermetallic compounds from first principles［J］.Physica B:Condensed Matter，2012，407(1):96-102.

［28］Wasserman E F.Ferromagnetic Materials［M］.Amsterdam:Elsevier Science，1990.

［29］Gulsern O，Cohen R E.High-pressure thermoelasticity of body-centered-cubic tantalum［J］.Phys Rev B，2002，65:064103.

［30］Pettifor D G.Theoretical predictions of structure and related properties of intermetallics［J］.Mater Sci Tech，1992，8:345-349.