运用一种集成方法的低碳供应商选择

钟映竑，张培新

(广东工业大学管理学院，广州 510520)

在绿色供应链中，供应商的选择扮演着很重要的角色。目前，许多学者从环境可持续发展的角度来研究绿色供应链的供应商选择问题，但是在此过程中很少研究考虑碳排放量问题。Trucost［1］的调查显示在供应链中只有19%的温室气体是直接来自企业的运营活动，81%的排放量是间接来源。因此，供应商的选择在减少供应链中的碳排放量具有一定的重要作用。近年来，一些学者对供应商选择问题进行了深入的研究。Amid和 O’Brien等［2］建立了只考虑成本、质量2个目标的模糊线性规划模;Yücel和 Güneri［3］为供应商评价提出了一种加权模糊规划方法，该方法运用了TOPSIS和模糊线性规划，且只考虑以成本、质量、按时交货率为目标;Amid等［4］建立了只考虑成本、质量、价格为目标且需求是确定的多目标规划，并用极大－极小权重模型求解;Krishnendu［5］考虑了碳排放因素和模糊需求，建立了只考虑总成本、质量拒绝率、延迟交货率、碳排放为目标的多目标规划，并用加权规划对其求解，得出各供应商的订购量。

本文在文献［5］的基础上，首先把文献［5］中已计算的指标权重应用到FTOPSIS中得出各备选供应商的价值，然后以总价值、总成本、质量拒绝率、延迟交货率、碳排放5个指标为目标函数，建立模糊多目标规划模型，运用极大－极小权重模型来求解，得出最优订购量。该方法的优点是:能够有效处理决策过程中的不确定性，保持各目标函数的隶属度与其权重之间的一致性，更能反映决策者的偏好。

1 模糊集和语言变量

Zadeh［6］提出了模糊集理论［7］，该理论用来解决决策过程中信息的模糊性。他在文中运用三角模糊数来评价决策者的偏好，其优点是容易理解且计算量很小。把(a，b，c)定义为一个三角模糊数，其中a≤b≤c。则三角模糊数运算的一些基本规则为

2个三角模糊数之间的距离公式为

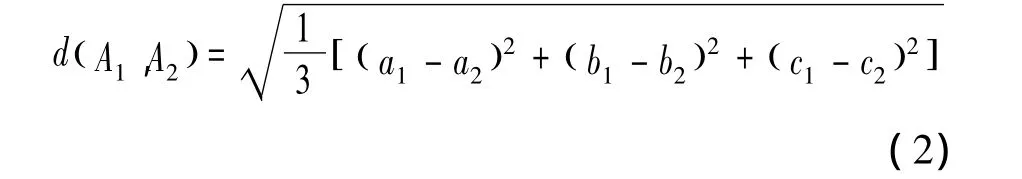
语言变量是一种用人类语言来表示某一客观对象重要程度的变量。Wang和Elhag［8］在研究中表明:语言变量有7个评价等级标准，即非常差(VP)、差(P)、较差(MP)、中等(M)、较好(MG)、好(G)、非常好(VG)，并且每个等级都对应一个三角模糊数。当决策者在对各方案的指标进行评价时，往往会遇到模糊性指标，这时决策者就会采用语义判断来表示，则评价结果就会受到决策者主观判断的影响，而语言变量的引入正好可以解决该类问题。表1表示语言变量的7个评价等级标准。

表1 评价指标语意变量及三角模糊数

2 模型的建立

2.1 运用FTOPSIS计算低碳供应商的价值

FTOPSIS是将TOPSIS和模糊集理论相结合的一种非常典型的多准则决策方法。与其他方法相比FTOPSIS优点突出，不仅延续了TOPSIS的简单易用的特点，而且能够有效处理决策中的模糊信息，其步骤如下:

1)根据表1的语言变量对应的三角模糊数来建立初始模糊矩阵，i=1，2，…，m;j=1，2，…，n。

2)根据式(3)

其中:I1为效益型指标;I2为成本型指标;将矩阵标准化为，其中 i=1，2，…，m，j=1，2，…，n。

5)分别计算各个备选方案到正理想解和负理想解的距离:

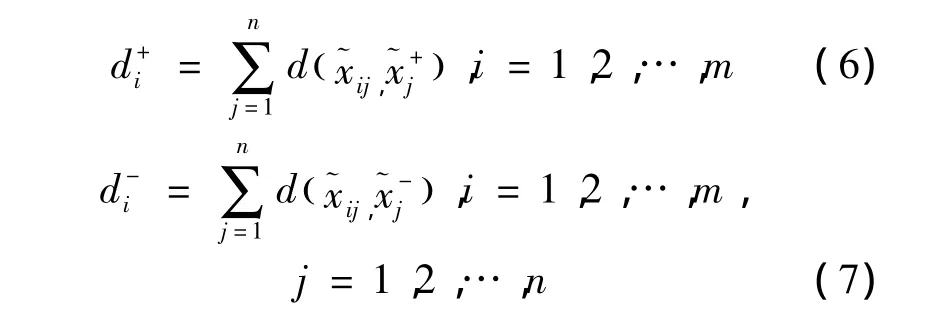
6)计算各方案综合评价指数，然后对其标准化，即各备选供应商的价值。

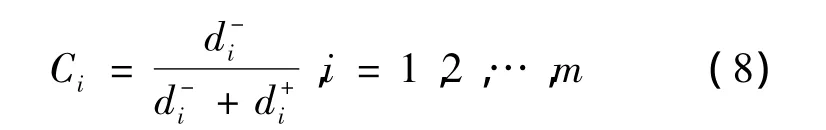
2.2 优化低碳供应商的订购量

2.2.1 模糊多目标规划模型

Zimmermann［9］提出了用模糊规划来解决多目标规划问题。因此，在低碳供应商的选择问题中，若供应商的总价值、总成本、质量拒绝率、延迟交货率、碳排放以及需求量均是模糊的，则可以建立以下模糊线性规划模型(FLP):

其中，xi≥0且为整数。这里，～表示环境是模糊的分别为决策者想达到的理想的总价值、总成本、质量拒绝率、延迟交货率、碳排放水平。在约束条件中，式(14)为满足的模糊需求约束，式(15)～(17)是确定性的硬约束。

2.2.2 确定隶属度函数

Bellman和 Zadeh［10］是目标函数和约束条件的隶属度函数的交集，即可变为如下形式:μS(x)=μZ(X)∩μC(x)=min μZ(x);μC(x[])。其中 μZ(X)，μC(x)，μS(x)分别表示目标、约束和解的隶属度函数，则含有J个目标和K个约束的模糊多目标规划模型的解为:

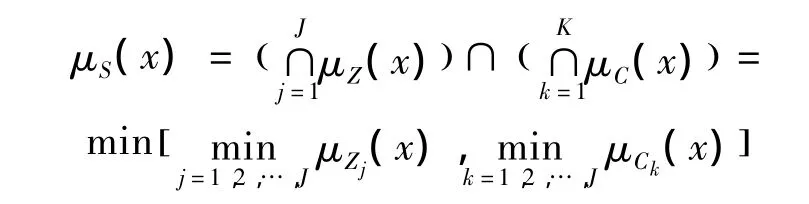
因此，模糊多目标规划求解的重点就是求隶属度函数μl(x)。本文对目标函数取最小值及约束取小于等于的情形采用降半梯形分布的隶属度函数;对于目标函数求最大值的采用升半梯形分布的隶属度函数。

其相应的目标隶属度函数表达式为:

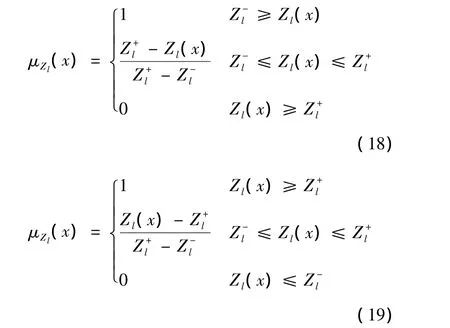
式(18)表示目标函数求最小值，式(19)表示求目标函数最大值。其中:Zl(x)是第l目标函数的值是目标函数Zl(x)偏离上线值;是目标函数Zl(x)的偏离下限值。对于约束条件的隶属度函数如下:

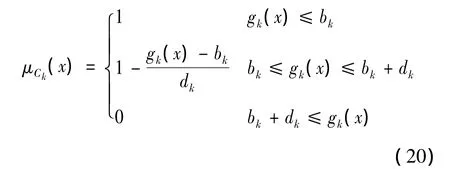
式(20)中:dk是采购商设定的常数，表示其对违反约束的容忍程度。

为了求解目标函数的隶属度函数，首先要求解目标函数Zl(x)偏离上线值 Z+l和目标函数Zl(x)的偏离下限值Z－l。本文采用Zimmermann提出的求解方法，即:

其中:x≥0 且为整数;l=1，2，…，L;k=1，2，…，K。然后，把求得的和代入式(18)、(19)中就可求出各目标函数的隶属度。

2.2.3 模型求解

根据Lin［11］提出的极大－极小权重模型，可以把上述模糊多目标规划问题转变为确定的单目标规划。该方法能够保持各目标函数的隶属度与其权重之间的一致性，更能反映决策者的偏好。其具体形式如下:

其中:Wl≥0;Wk≥0。

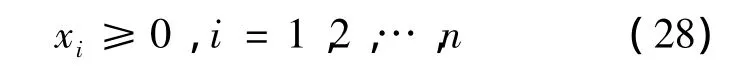
根据上述的求解过程，可以得到低碳供应商选择模型的最优解，同时决策者也可以很好地衡量各目标的重要程度。

3 算例的应用

3.1 运用FTOPSIS计算各备选低碳供应商的价值

某制造商准备从4家供应商采购同一种产品，在文献［5］的相关数据基础上得到如下结果:

1)表2是3位专家各自对4个备选供应商各个指标的评价。

2)根据文献［5］中各目标的权重 W=(0.257，0.224，0.184，0.202，0.133)和式(4)，求出加权标准化单因素判断矩阵(见表3)。

表2 专家对3个备选供应商各个指标的评价

表3 加权标准化单因素判断矩阵

3)根据式(6)、(7)可得各方案到正理想解和负理想解的距离为:

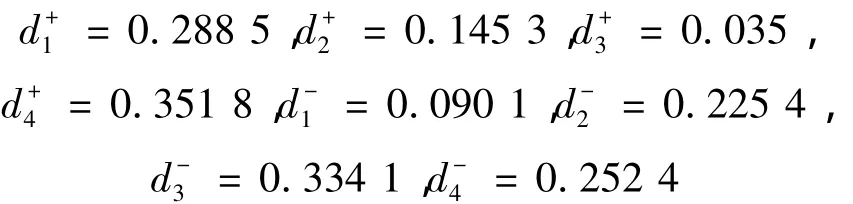
4)根据式(8)可以计算出各个方案与理想解的标准化相对接近度为:

由以上可得这4个供应商的价值分别是0.1097，0.2803，0.4174，0.1926。各供应商订单量的分配会影响总价值，当总价值最大时，订购量的分配将在下一节进行说明。

3.2 优化各低碳供应商的订购量

根据各专家的评价可知:在该制造业中其总价值和总成本的重要程度是一样的，即目标函数总价值和总成本的权重相同。本文运用文献［5］中的权重 W=(0.257，0.224，0.184，0.202，0.133)，并使 W总价值=W成本=0.257，对以上权重进行标准化，即 W'=(0.205，0.205，0.178，0.146，0.160，0.106)，然后根据式(22)～ (28)可以得到极大－极小权重模型如下:

其中 x1≥0，x2≥0，x3≥0，x4≥0，且 x1，x2，x3，x4都是整数。运用LINGO11.0求解以上规划可得:

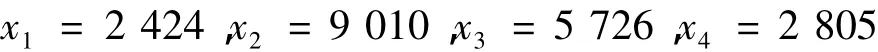
由以上知供应商的总价值为5721.7，总成本为108933，质量拒绝率是 618.22，延迟交货率为823.2，碳排放量是 28025。与文献［5］所提方法相比可知:本文中的总成本和拒绝率都较大，但是延迟交货率和碳排放量相对较小。说明运用该方法优化订购量更具低碳性，同时总价值、总成本、拒绝率、延迟交货率、碳排放的隶属度分别为0.5551，0.5510，0.5351，0.3954，0.4335，即μ总价值= μ成本＞ μ质量＞ μ碳排放＞ μ交货期，这与权重W总价值=W成本＞W质量＞W碳排放＞W交货期的顺序保持一致，更具现实意义。

3.3 敏感性分析

使总价值的权重分别和质量、交货期、碳排放和需求的权重相等，然后对这些权重进行标准化并代入模糊规划模型，得到的结果见表4。

表4 敏感性分析

从表4可以看出当 W总价值=W成本＞W质量＞W碳排放＞ W交货期时，μ总价值= μ成本＞ μ质量＞ μ碳排放＞μ交货期;当 W总价值=W质量＞W碳排放＞W交货期时，μ成本＞μ总价值= μ质量＞ μ碳排放＞ μ交货期;当 W成本＞ W质量＞W碳排放＞W总价值=W交货期时，μ成本＞ μ质量＞ μ碳排放＞μ总价值=μ交货期;当 W成本＞W质量＞W总价值=W碳排放＞W交货期时，μ成本＞ μ质量＞ μ总价值= μ碳排放＞ μ交货期。可以得到:无论总价值的权重如何变化，总成本、拒绝率、延迟交货率、碳排放的隶属度都和其权重的大小顺序保持一致，即 μ成本＞ μ质量＞ μ碳排放＞μ交货期。这表明这几个目标函数的隶属度和专家的偏好是一致的，也使决策的结果更准确。同时从表4还可得出:在这几种情况下本文方法的总成本和拒绝率都较文献［5］的大，延迟交货率和碳排放量都较文献［5］的小。尽管本文方法的总成本略高，但从长远利益来看还是较优，因为本文方法把环境作为企业长期发展的一个重要因素，这样能充分提升企业形象，从而企业的发展也就更长久，潜在的价值也就会慢慢地发挥作用，同时国家也会根据低碳环保相关政策给予一定的奖励、补贴等。

4 结束语

随着低碳经济的大力发展，企业对低碳原材料的要求越来越高，为了减少企业本身或所在供应链上的碳排放量，选择合适的供应商是关键。本文在文献［5］的基础上，提出了一种集成的低碳供应商评价方法，为决策者提供了一种决策工具。该方法运用文献［5］中的权重，首先把该权重放到FTOPSIS方法中计算出各备选供应商的价值;然后把总价值作为其中的一个目标函数建立了模糊多目标规划模型，并用极大－极小权重模型对其进行求解，优化供应商的产品订购量;最后对结果进行相关的敏感性分析来说明该方法的优越性。但本文仍有不足，例如:①没有考虑订购数量的折扣且只考虑了一种产品;②该方法是在不允许缺货且提前期是常数的条件下提出的;③ 碳排放计量是现在国内外研究的一个热点，也是低碳供应链研究的一个难题，而本文中的碳排放是一个常数，在以后的研究中可以考虑模糊碳排放因素;④在碳交易市场下，不同的碳税价格对企业业绩有较大的影响，在后续的研究中还可以考虑在不同形式的碳税价格下对供应商以及订购量的影响。

［1］Trucost.Carbon emissions-measuring the risks［EB/OL］.［2009］.www.nsf.org/business/sustainability/SUS_NSF_Trucost_Report.pdf.

［2］Amid A，Ghodsypour S H，O’Brien C.Fuzzy multi-objective linear model for supplier selection in a supply chain［J］.International Journal of Production Economics，2006，104(2):394 －407.

［3］Yücel A，Güneri A F.A weighted additive fuzzy programming approach for multi-criteria supplier selection［J］.Expert Systems with Applications，2010，38(5):6281－6286.

［4］Amid A，Ghodsypour S H，O’Brien C.A weighted maxmin model for fuzzy multi-objective supplier Selection in a supply chain［J］.International Journal of Production E-conomics，2011，131(1):139 －145.

［5］Krishnendu S，Ravi S，Surendra S Y，et al.Thakur.Supplier selection using fuzzy AHP and fuzzy multi-objective linear programming for developing low carbon supply chain［J］.Expert Systems with Applications，2012，39(9):8182－8192.

［6］Zadeh L A.Fuzzy sets［J］.Information and Control，1965(8):338－353.

［7］关峻，李京文.基于模糊集理论的生产系统柔性度量研究［J］.武汉理工大学学报，2009，31(13):153 －156.

［8］Wang Y M，Elhag T M S.Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment［J］.Expert Systems with Applications，2006，31(2):309－19.

［9］Zimmermann H J.Fuzzy programming and linear programming with several objective functions［J］.Fuzzy Sets and Systems，1978，1(1):45 －56.

［10］Bellman R E，Zadeh L A.Decision making in a fuzzy environment［J］.Management Science，1970，17(4):141－164.

［11］Lin C C.A weighted max-min model for fuzzy goal programming［J］.Fuzzy Sets and Systems，2004，142(3):407 －420.