基于时序模糊软集的群决策新方法
钱庆庆,吴 涛,宋 雷,许文浩
(安徽大学 a.数学科学学院;b.文典学院,合肥 230039)
随着科学研究的不断发展,人们发现很多问题往往存在着不确定性和模糊性,它们难以用传统的数学工具加以描述和分析。为了研究并解决这些问题,模糊集理论[1-2]、区间数理论[3]、粗糙集理论[4]和概率论[5]等不确定理论应运而生并得到了很好的发展和应用,然而这些理论自身也存在着固有的局限性[7]。为了克服这些理论的局限性,Molodtsov首次提出了软集[8]的概念,它是一种全新的处理不确定性的数学工具。由于软集理论自身的优越性,即能够更加灵活、细腻地刻画客观世界的不确定性,近年来,人们已将软集理论与其他不确定理论进行了结合并提出了模糊软集、粗糙软集等概念[9-11]。文献[12 -13]研究了软集之间的各种运算法则(交、并、补、子集等)。文献[14-15]重新定义了文献[7]中的软集概念并讨论了软集间的运算法则,且在此基础上定义了软矩阵并讨论了软矩阵的相关性质及运算。文献[16-18]分别将软集概念推广到模糊软集、直觉模糊软集和区间型直觉模糊软集,并讨论了各自的相关性质。同时通过设定阈值向量构造水平软集[16],将模糊软集和直觉模糊软集转化为经典软集,再通过计算论域中各对象的机会值得到最优决策。
然而,上述研究基本上是从静态角度去研究软集理论和模糊软集理论,而在实际生活中,时间的作用无法忽略。这使得决策者在决策过程中需要对问题进行动态的分析。因此,在此基础上,文献[19]在模糊软集中引入时间参数,并将其推广到时序模糊软集。理论上,时序模糊软集反映的是决策信息随时间变化的情况,不同时刻所对应的模糊软集对最终的决策影响并不相同。据此提出了一种基于指数衰减模型的时间权重确定方法,认为:不同时刻决策者所掌握的信息不同,越靠近最终决策时刻,掌握信息量越大,对最终决策的影响越大,时间权重越大;反之越远离最终决策时刻,对最终决策的影响越小,时间权重越小。但这种赋权方法具有主观随意性,不能反映出对象本身在动态状况下的特点,因此需要提供一种新的时间权重赋值方法。属性值因动态产生的这种变化通过横向观察每个对象在不同时刻的决策信息值可以反映出对象自身保持前一时刻属性值的能力,而纵向观察所有对象在同一时刻下的决策信息值则反映出对象间不同时刻的好坏差异程度,因此,将这种能力和差异程度综合为对象集整体的稳定程度。在同一时刻下,对象集越稳定表明对象间差异较小,不能明显反映出对象间的优劣;反之,越不稳定即离散程度越大,表明对象间有较明显差异。鉴于此,本文首先考虑到不同属性间物理刚量的差异,对每一个模糊软集进行规范化预处理,将所有属性归一为综合属性,通过计算平均绝对离差获得不同时刻模糊软集的权重值,然后通过集成思想和水平软集的方法,给出了一种新的基于时序模糊软集的群决策方法。
1 预备知识
定义1(软集) 设U是非空有限集,E是一个参数集合,P(U)是U上的幂集,且A⊂E,则序对(F,A)称为U上的一个软集,其中F:A→P(U)为一个参数子集A到P(U)的映射[8]。
定义2(模糊软集) 设U是一个非空论域,E是一个参数集合,I=[0,1],IU表示U上的所有模糊集的全体,称序对(F,E)为论域U上的模糊软集(FSs),其中F:E→IU为一个从参数集E到IU的映射,即对∀e∈E[20],
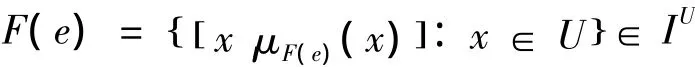
其中,μF(e)(x)表示元素x属于模糊集F(e)的隶属度。
定义3(时序模糊软集) 设U是非空论域,E是参数集,T是时间集合,I=[0,1],IU表示 U 上的所有模糊集的全体,称序对(F,E×T)为论域U上的时序模糊软集(TSFSs),其中F:E×T→IU为一个参数集E×T到U上的映射,即对∀(e,t)∈E × T,F(e,t)= {〈x,μF(e,t)(x)〉:x∈U}∈IU表示元素 x 属于模糊集 F(e,t)的隶属度[19]。
文献[19]指出:时序模糊软集就是一系列模糊软集按照时间参数排列形成的整体,即对于固定时刻,时序模糊软集其实就是一个普通的模糊软集。根据模糊软集的特点,每一个模糊软集都可以用一个矩阵的形式表示出来,记作模糊软矩阵(FSM),即
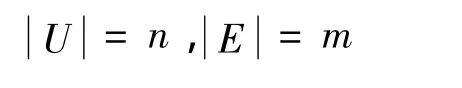
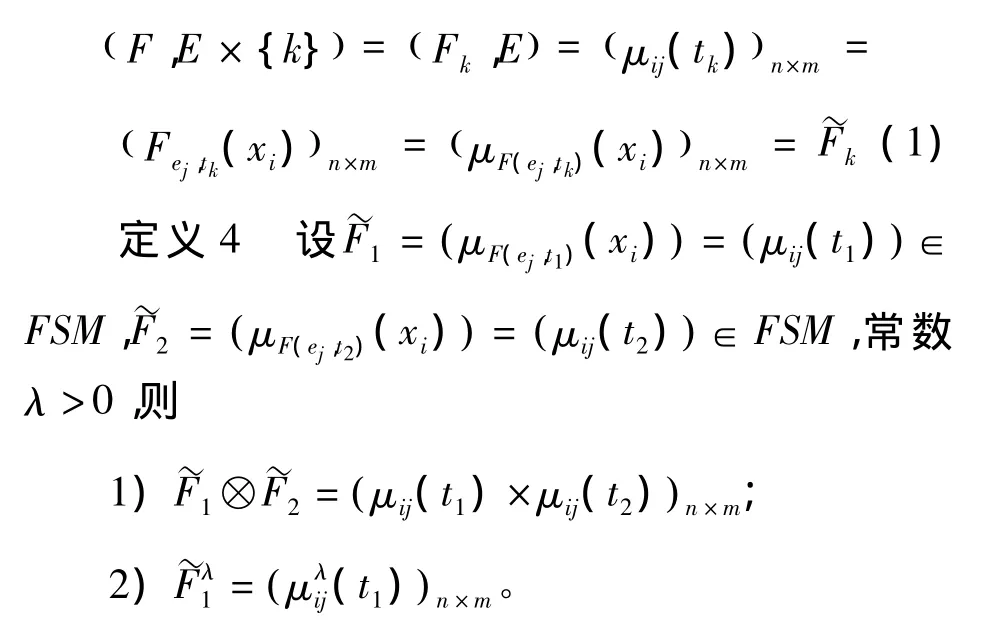
基于上述的基本运算法则,可以定义时序模糊加权几何平均算子。

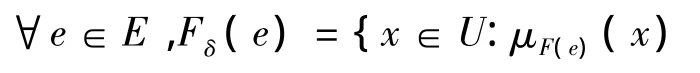
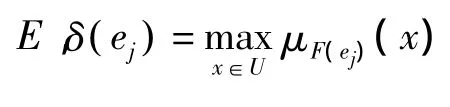
2 时序模糊软集的决策方法
2.1 模糊软集的规范化预处理
一般情况下,属性类型分为效益型和成本型,而属性类型的不同会在决策过程中造成难以避免的影响。为了减少这样的影响,需要对每一个模糊软集进行规范化预处理[2]的过程。
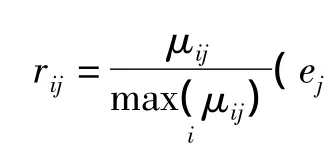
2.2 时间权重的确定方法
一般而言,对象集的稳定程度能反映出对象彼此之间的差异。在动态情况下,这种差异也表明了不同对象保持初始状态的能力及对象间的优劣差异程度。所以,对象集越稳定表明对象间差异较小,不能反映出对象间的显著优劣;反之,越不稳定即离散程度越大,表明对象间有较明显差异。把这种时间的作用转化为权重,然后给定时间权重。考虑到若计算不同对象各时间各属性下的差异,将大大增加时间和空间上的复杂度,这里简化算法,将多属性集成为一个综合属性从而达到简化的效果。下面考虑时序模糊多属性决策问题:

假设属性权重信息完全未知,记为 w=(w1,w2,…,wm),其中wj表示第j个属性权重。文献[2]中给出属性赋权方法:w1=(1-α)m+α,wj=(1- α)m,j≠1 且 α∈[0,1]。
定义综合属性为e,则对象xi在tk时刻下的综合属性值为
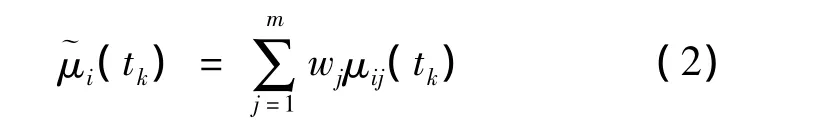
tk时刻下的平均综合属性值为

tk时刻下的平均绝对离差为

根据“平均绝对离差M(tk)越大,该时刻时间权重越小,反之越大”的思想,给定权重公式:
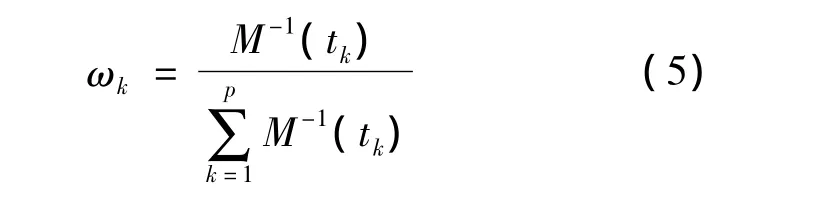
于是,得到基于时序模糊软集的决策方法的途径:
Step 1 根据属性的类型,利用本文2.1节的方法对原时序模糊软集进行规范化预处理;
Step 2 利用式(2)、(3)、(4)分别计算综合属性值、平均综合属性值及平均离差;
Step 3 利用式(5)计算各时刻下的属性值,并代入式(1)将时序模糊软集集成为综合模糊软集;
Step 4 计算最大值阈值向量并根据定义计算最大值水平软集;
Step 5 计算每个对象的机会值,从而得到最优决策。
3 举例说明
考虑航天设备的评估问题,有4种航天设备U={x1,x2,x3,x4}及评估指标(属性)E={e1,e2,e3,e4},所有指标均为效益型。对这4种航天设备进行了为期 4 周 T={t1,t2,t3,t4}的考查,并将考核结果以时序模糊软集的形式给出(见表1)。
因为4种指标(属性)都是效益型,所以将表1中4个模糊软集利用本文2.1节的方法进行规范化处理,得到规范化模糊软集(见表2)。
这里取 α=0.2,则属性权重为 w=(0.4,0.2,0.2,0.2),然后利用式(2)、(3)、(4)分别计算各对象各时刻下的综合属性及各时刻下的平均综合属性值(tk)、平均绝对离差M(tk),再利用式(5)计算各时间权重ωk,得到相关数据(见表3)。
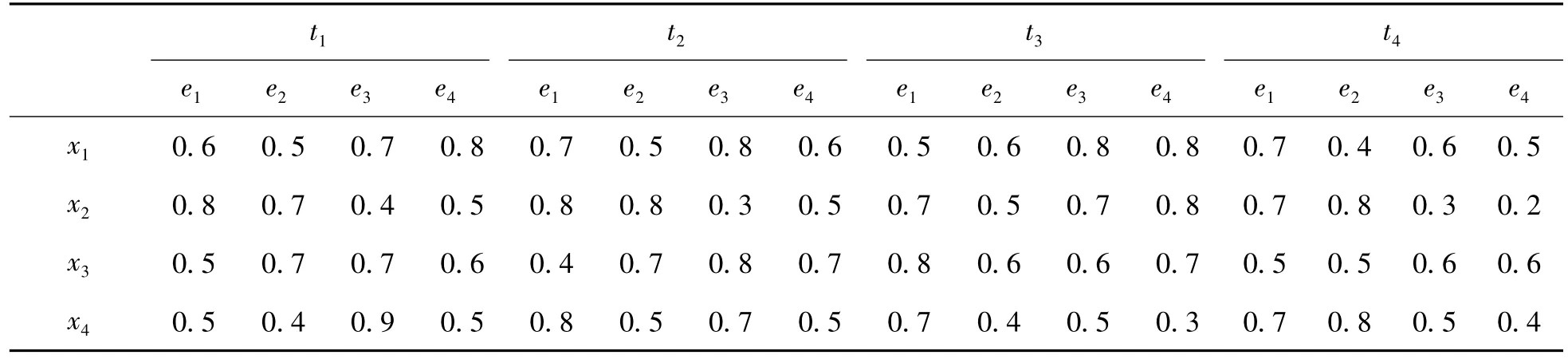
表1 时序模糊软集

表2 规范化模糊软集

表3 相关数据
由表3知:时间权重向量为 ω={0.2400,0.4171,0.1304,0.2125},再利用式(1)将时序模糊软集集成为综合模糊软集(见表4)。
计算最大值阈值向量为:δ(E)={0.9827,0.9765,0.9415,0.9172},从而得到最大值水平软集。计算各航空设备的机会值:S1=1,S2=2,S3=1,S4=0,则最优航空设备是 x2。
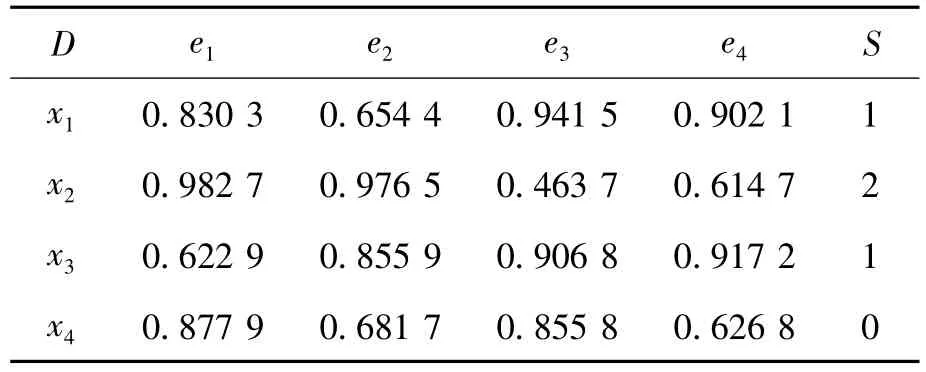
表4 综合模糊软集及机会值
4 结束语
本文主要研究时序模糊软集,考虑时间在决策过程中所产生的影响。随着时间的推移,不同对象的同一属性值必定有所改变。这种改变一方面可以反映对象之间的好坏差异;另一方面也可以表现出对象保持原有属性值的能力。本文基于这2种考虑,将这种差异和能力用可以量化的对象集整体在不同时刻下的稳定程度来表示。由于不同属性的量纲不同,所以先规范化处理原模糊软集,再将不同属性综合为综合属性,然后通过平均绝对离差量化差异性并确定时间权重,利用集成思想及水平软集的方法计算机会值,最后确定最优对象。
[1]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338 -353.
[2]Xu Z S.Uncertain Multiple Attribute Decision Making:Methods and Application[M].Beijing:Press of Tsinghua University,2004.
[3]Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87 -96.
[4]Pawlak Z.Rough sets[J].International Journal of Information and Computer Sciences,1982,11:341 - 356.
[5]Miao B Q,Hu T Z.Probability Theory(The Second Edition)[M].Hefei:Press of University of Science and Technology of China,2009.
[6]吴永,邵明阳.重尾索赔下常利力更新风险模型的破产概率[J].重庆理工大学学报:自然科学版,2010,24(10):97-100.
[7]Molodtsov D.Soft set theory-First results[J].Computers and Mathematics with Application,1999,37:19 -31.
[8]Maji P K,Biswas R,Roy A R.Soft sets theory[J].Computers and Mathematics with Application,2003,45:555 -562.
[9]Ali M I.A note on soft sets,rough soft sets and fuzzy soft sets[J].Applied Soft Computing,2011,11:3329 -3332.
[10]Feng F,Li C X,et al.Soft sets combined with fuzzy sets and rough sets:A tentative approach[J].Soft Computing,2010,4:899 -911.
[11]Feng F,Liu X Y,et al.Soft sets and soft rough sets[J].Information Sciences 2011,181:1125 -1137.
[12]Ali M I,Feng F,et al.On some new operations in soft set theory[J].Computers and Mathematics with Applications,2009,57:1547 -1553.
[13]Sezgin A,Atagun A O.On operations of sets[J].Computers and Mathematics with Application,2011,61:1457-1467.
[14]Cagman N,Enginoglu S.Soft set theory and unint decision making[J].European Journal of Operational Research,2010,207:848 -855.
[15]Cagman N,Enginoglu S.Soft matrix theory and its decision making[J].Computers and Mathematics with Applications,2010,59:3308 -3314.
[16]Feng Feng,Young Bae Jun,et al.An adjustable approach to fuzzy soft set based decision making[J].Journal of Computational and Applied Mathematics,2010,234:10-20.
[17]Jiang Y CH,Tang Y,Chen Q M.An adjustable approach to intuitionsitic fuzzy soft sets based decision making[J].Applied Mathematical modeling,2011,35:824 -836.
[18]Jiang Y CH,Tang Y,et al.Interval-valued intuitionisitic fuzzy soft sets and their properties[J].Computers and Mathematics with Applications,2010,60:906 -918.
[19]Mao J J,Yao D B,et al.Group decision-making method based on time-series fuzzy soft set[J].Systems Engineering-Theory & Practice,2014,34(1):182 -189.
[20]Majumdar P,Samanta S K,On similarity measures of fuzzy soft sets[J].International Journal of Advances in Soft Computing and Its Application,2011,2:1 -8.

