升降舵速率饱和引发的纵向PIO趋势预测方法
刘瑜, 王海维, 贾晓鹏
(1.中国飞行试验研究院 飞机所, 陕西 西安 710089;2.西安飞机工业(集团)有限责任公司 技术中心, 陕西 西安 710089)
0 引言
驾驶员诱发振荡(PIO)是由于飞机与驾驶员间不良的耦合关系而引发的一种持续的或失控的人机耦合振荡,即人机闭环系统出现了不稳定[1]。
随着航空技术的发展,飞机的飞行包线不断扩大,任务需求逐渐扩充并综合化,为了使飞机在性能、品质、机敏性等方面获得质的飞跃,广泛采用了放宽静稳定性技术和高增稳电传飞控,系统功能增强,复杂性显著提高。另外,电传飞机的操纵面大都较小,对小的操纵力和偏转指令很敏感,舵面偏转频繁,偏转速率非常快,且由于操纵信息都是电信号传递,使座舱操纵装置不能向驾驶员直接反馈操纵面速率限制或位移限制等信息,就可能导致PIO现象的发生[2]。
据国内外相关资料统计,由舵面速率饱和引发的PIO事件已成为电传飞机发生飞行事故的首要因素,典型事件就是瑞典的JAS-39和美国的F-22都曾在着陆期间发生过由升降舵速率饱和引发的纵向PIO,最终导致飞行等级事故的发生[3]。为确保我国型号试飞安全,开展速率饱和及由其引发的PIO趋势预测技术研究意义重大。
本文针对由升降舵速率饱和引发的纵向PIO趋势预测技术开展研究,结合飞控系统稳定裕度概念提出了一种时域预测方法,并基于YF12飞机空中加油任务的仿真数据对其进行了分析与验证。
1 速率饱和成因
当飞控系统舵机超出其速率限制指令时,认为该舵机发生了舵面速率饱和。一旦出现舵面速率饱和,舵机就不会对同一方向的附加指令作出响应,从而导致飞行品质降级,甚至引发PIO趋势,最终可能发生飞行等级事故[4]。
高增稳电传飞控产生速率限制有软件和硬件两种,速率限制器在飞控系统中的典型应用如图1所示。软件速率限制主要是指令通道软件速率限制和舵机软件速率限制,它们都是为了防止舵机出现饱和而有意设计的[4]。硬件速率限制主要源于舵机和操纵面的物理或液压限制。现代高增稳电传飞机大都采用了放宽静稳定性技术,为补偿机体的稳定性,飞控系统会以不同幅值、不同速率的指令频繁地驱动操纵面,使得速率饱和对飞控系统的危害不可避免。尤其随着放宽静稳定度范围的扩大,对操纵面速率要求会更高,引发PIO趋势的几率也将大大增加。
2 预测方法分析
速率限制环节的动特性是非线性的,它的启动与否飞行员也是不可预知的,只与速率限制器启动频率或启动速率相关。当速率限制环节启动时,它会为系统引入相位延迟,并降低驾驶员操纵增益的幅值,使飞行员操纵与期望的飞机响应出现差异,引发飞行品质降级,甚至导致或促进人机闭环不稳定,或引发PIO趋势[5-6];否则,它不会对系统产生任何影响。
研究表明,速率限制器的饱和水平是预测和分析速率限制引发PIO问题的关键,它通常与速率限制环节引入人机闭环系统的相位延迟成比例。因此,通过分析速率限制环节特性,找出衡量速率限制环节饱和水平的特征参数,将是预测由速率饱和引发PIO趋势的关键。
2.1 速率限制环节特性分析
当发生舵面速率饱和时,速率限制环节通常可描述为正弦输入/三角输出,其输入/输出特性如图2所示。图中,Xi(t)为输入,Xo(t)为输出,Xi为输入的幅值,Xo为输出的幅值,ti为输入时间,to为输出时间,td为输入输出的延迟时间。

图2 速率限制环节的输入输出特性Fig.2 Input and output characteristics of the rate limiter
速率限制环节的幅值比ARLE和相位差φRLE分别为:
(1)
φRLE=-arccosk*
(2)

(3)

(4)

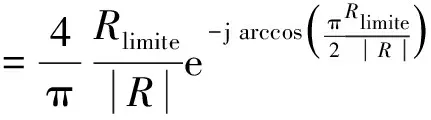
(5)
上式表明,速率限制器饱和时的频域特性可由速率限制器输入和输出信号的速率比(|R|/Rlimite)进行描述。
图3给出了Rlimite=1 (°)/s时速率限制环节的频域响应曲线。
从图中可以看出:|R|/Rlimite≥1时速率限制环节启动;否则不启动。当速率限制环节未启动时,幅值比和相位差都为零,对系统无影响。当速率限制环节启动时,在过渡段,会突然引入很大的附加相位延迟,操纵幅值也有轻微的减小;进入高饱和段后,引入的相位延迟和操纵幅值减小水平直接与|R|/Rlimite的大小相关,即|R|/Rlimite直接反映了速率限制器的饱和水平。因此,可将|R|/Rlimite作为描述速率限制器饱和水平的特征参数。
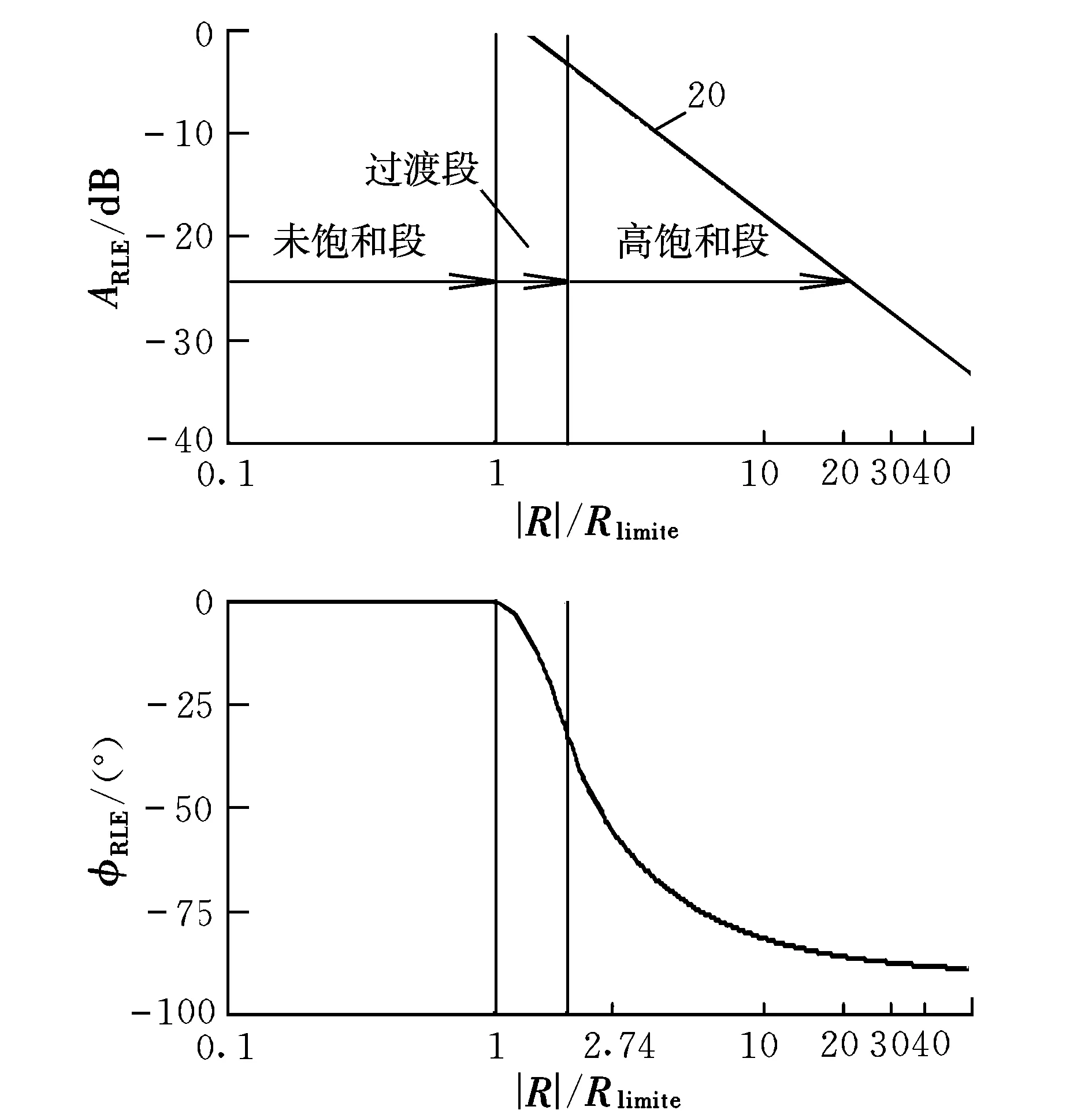
图3 速率限制环节的频响Fig.3 Frequency-domain response of the rate limiter
2.2 速率限制环节对人机闭环系统的影响
本文以如图4所示的系统为例,分析速率限制环节对人机闭环系统的影响。
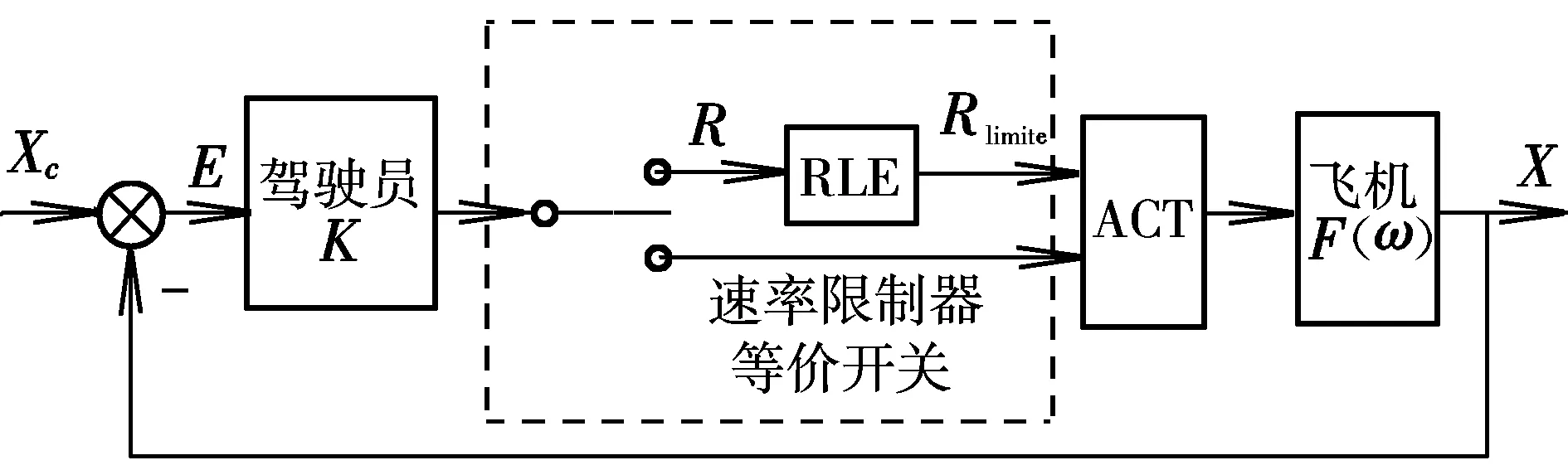
图4 系统速率限制简化框图Fig.4 Simplified diagram of the rate limiter in system
速率限制环节未开启时,开环系统和闭环系统的最大输入速率分别如式(6)和式(7),相位如
式(8):
|R|OLoff=XcKω
(6)

(7)
φCLoff=φOLoff+φlead=φF+φlead
(8)
式中,φlead为闭环系统引入的相位超前;φF为系统本身的相位差[7]。
闭环系统中速率限制环节开启时,其输入速率的最大幅值和人机闭环系统的总相位分别为:
|R|CLon=|R|OLon[1+KF(ω)]
(9)
φCLon=φF+φRLECLon
(10)
其中:
(11)
综合式(9)~ 式(11)可得,人机闭环系统的速率限制器发生饱和时,速率限制器的输入速率会突然增大,且会引入附加相位延迟,出现跳跃谐振现象,且其引入相位延迟的多少直接与Rlimite/|R|CLon的大小相关。
2.3 预测准则
在频域中,人机系统的开环交叉频率ωc广泛用作系统相对稳定性计算参数,随着开环增益的增大,ωc增加,相位裕度减小,系统稳定性减弱。当相位裕度减小到零,甚至到负值时,将会导致人机闭环系统不稳定。因此,提出将预测人机闭环系统PIO趋势与稳定裕度相结合,用ωc与速率限制环节启动频率ωonset之比评估速率饱和对人机闭环稳定性的影响,进而预测速率饱和是否会导致人机闭环系统不稳定或引发PIO趋势[8-9]。
综合式(4)和式(5),可将速率限制环节启动后引入的相位延迟表示为:
(12)
那么,当人机闭环系统到达稳定边界时,人机闭环系统的相位裕度将在ωc处或|R|=Rlimite处被由速率饱和引入的附加相位延迟消耗殆尽,变为0,甚至负值。因此,为确保人机闭环系统稳定,必须满足:
(13)
上式表明,只要提供速率限制器的输入速率信号,即可通过计算R*确定速率限制器的饱和水平,进而确定舵面速率饱和为人机闭环系统引入的相位延迟量,最终确定人机闭环系统稳定性,预测是否引发PIO趋势。
图5为由式(13)得到的预测边界判据图,图中曲线即为发生人机闭环系统不稳定和引发PIO趋势的临界条件,边界线左方为发生PIO趋势的区域。
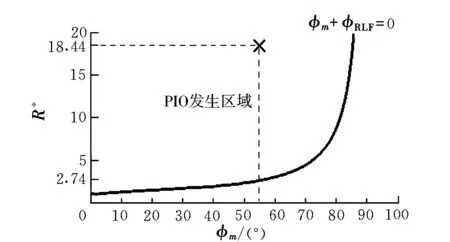
图5 PIO趋势预测边界Fig.5 Predicting boundary of the PIO tendency
3 仿真验证
下面基于图6所示系统的仿真数据,利用本文提到的R*准则对其进行分析和PIO趋势预测,并通过与时域响应数据对比分析,验证该预测方法的正确性和合理性。
图6所示系统为YF12飞机进行空中加油任务时的纵向控制律简化框图。其中速率限制器位于俯仰阻尼器回路,其限制值为15 (°)/s[10],通过频域分析求得人机闭环系统的相位裕度为55°。由图5可知,R*≤2.74时人机闭环系统稳定,此时不会发生飞行品质降级或引发PIO趋势。
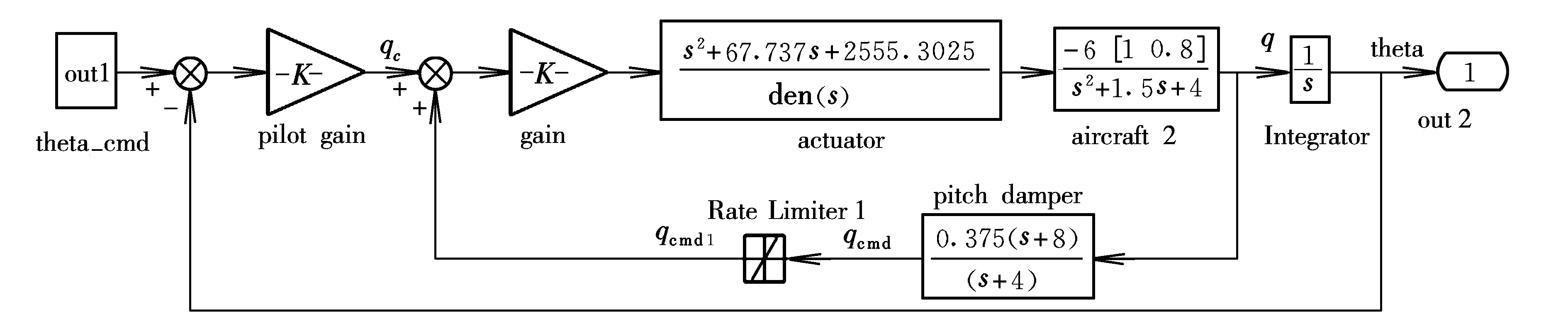
图6 YF12飞机空中加油任务纵向系统框图Fig.6 Longitudinal system structure of the YF12 in air-refueling task
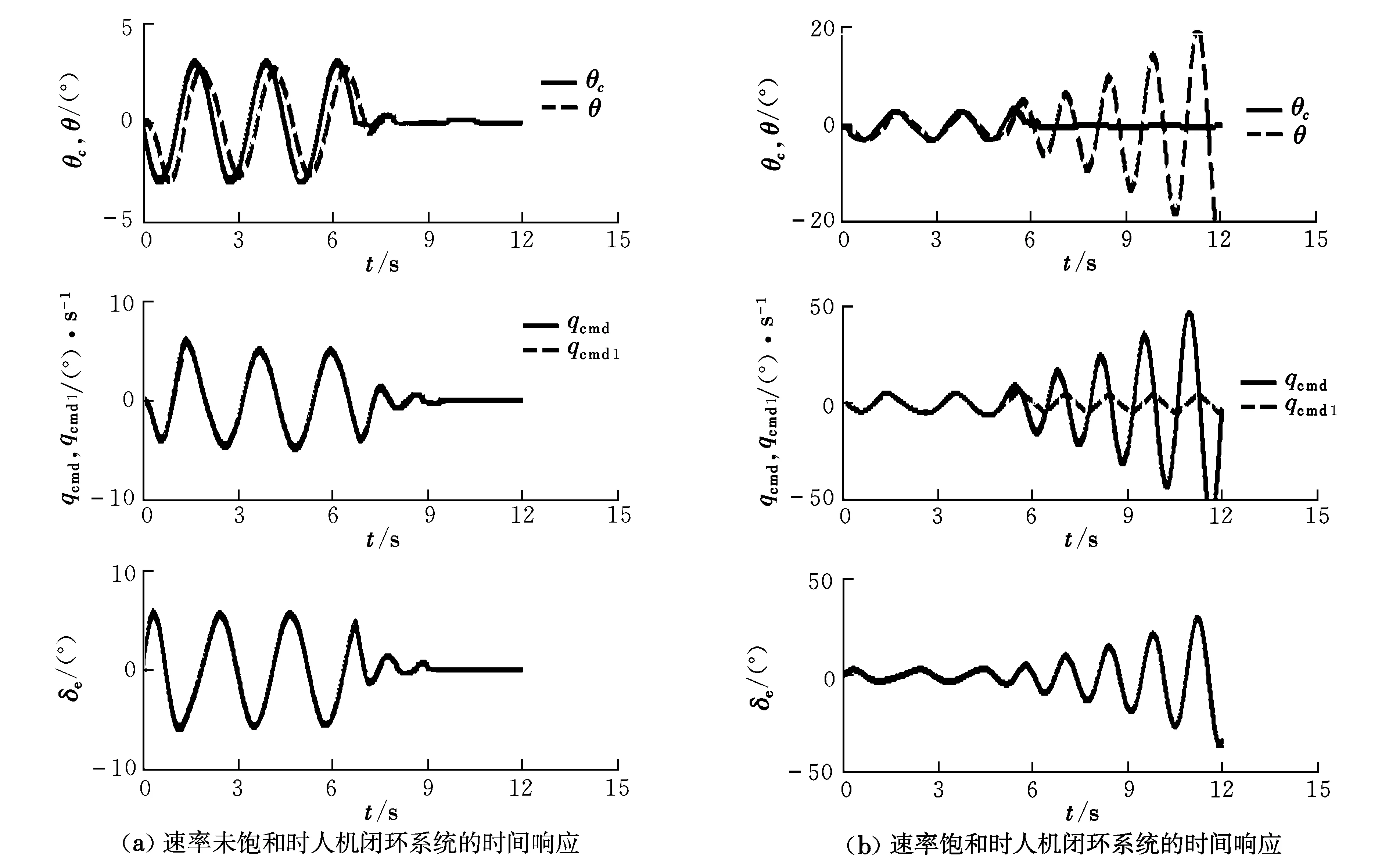
图7 YF12飞机空中加油任务的时间历程Fig.7 Response of the YF12 in air-refueling task
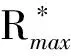

图8 R*准则计算结果Fig.8 Calculating results of the R* criterion
综上所述,通过对图6所示YF12飞机在不同任务频率进行空中加油任务的人机闭环系统特性对比分析结果表明,R*准则分析结果与时间响应曲线一致,从而证明了R*准则可用于确定是否发生速率饱和,并可通过饱和水平分析人机闭环系统的稳定性,进而预测速率饱和是否引发PIO趋势。
4 结束语
本文通过分析飞机速率限制成因及效应,结合飞控系统稳定裕度概念提出了一种预测由升降舵速率饱和引发纵向PIO趋势的时域方法,并基于YF12飞机的空中加油任务的仿真数据,用R*准则计算结果与飞机实际时间响应曲线进行了对比分析与验证。验证结果表明,在升降舵发生舵面速率饱和后约7 s内,R*以指数级增长至18.44,为人机闭环系统引入达85°的相位延迟,导致人机闭环系统不稳定,引发了纵向PIO事件,与飞机的实际响应一致。因此,说明R*准则分析结果正确、合理,能用于分析和预测由速率饱和引发的PIO趋势。另外,该准则是一个时域准则,且应用简单,可直接应用试飞数据进行在线预测,工程应用价值高,对确保型号试飞安全具有一定的意义。
参考文献:
[1] 高金源.飞机飞行品质[M].北京:国防工业出版社,2001:133-154.
[2] 张明廉.飞行控制系统[M].北京:航空工业出版社,1994: 347-358.
[3] Dornheim M A.Report pinpoints factors leading to the YF-22 crash [J].Aviation Week and Space Technology,1992,137(19):53-54.
[4] Ohmit E E.Augmented aircraft handing qualities [Z].Calspan Corporation,2006.
[5] 张爱民.自动化控制原理[M].北京:清华大学出版社,2007:244-298.
[6] Klyde D H,McRuer D T,Myers T T.PIO analysis with actuator rate limiting[R].AIAA-96-3432,1996.
[7] Hanke D.The influence of rate limiting elements in flight control systems on handling qualities[R].DLR-IB 111-93-61,1993.
[8] Hanke D.Criterion for predicting aircraft pilot coupling caused by rate limitation[R].DLR-IB 111-98-25,1998.
[9] Hanke D.Flight test evaluation and data analysis of rate limiting induced PIO’s[R].AIAA-2003-5317,2003.
[10] Duda H.Effects of rate limiting elements in flight control system:a new PIO criterion[R].AIAA-95-3304,1995.

