模块航天器姿态指向跟踪控制
李兆铭, 高永明, 牛亚峰, 黄勇, 李磊
(1.装备学院 研究生管理大队, 北京 101416;2.装备学院 信息装备系, 北京 101416;3.装备学院 航天装备系, 北京 101416)
0 引言
分离模块航天器是指将传统航天器拆解成若干个不同功能的模块,其构想是围绕整个任务,把传统的单个航天器的载荷、能源、通信、导航和计算处理等功能单元优化分解为多个模块,每个模块携带与航天任务相关的功能和资源,通过无线自组织网络组合成自由飞行空间集群系统[1-3]。其典型的代表即为F6(Future,Fast,Flexible,Fractionated,Free-Flying)项目。研究认为,应将空间能量获取及分配任务单独设计为一个模块,该模块通过空间反射镜聚光[4]等方式收集能量,并通过安装在该模块上的镜子系统[5]在轨道上形成充电区域,其余模块进入充电区域后,便可以接受其传输的能量。由于能量传输的定向性而对模块间方位有要求,为确保模块可以持续获得能量,有必要研究模块的姿态指向跟踪控制技术。
文献[6]针对姿态指向问题,考虑外部干扰和惯量不确定性设计了一种自适应滑模控制器,实现了受控航天器某个指向对运动目标的跟踪,但是其采用连续转动方式没有达到姿态快速指向,而且控制器设计较为复杂。文献[7]在描述姿态时采用欧拉角,很容易发生奇异。近年来,由于反步法可以解决Lyapunov方法缺乏构造性的问题而被用于航天器姿态控制系统的设计中。文献[8]利用反步法设计了一种自适应航天器姿态控制器,但文中没有考虑外界摄动干扰的影响。文献[9]提出了一种反步自适应滑模鲁棒容错控制方法,可以解决航天器在轨运行中存在的输入饱和等问题,但是其控制器设计比较复杂,控制器结构不够简洁。文献[10]利用反步法研究了挠性航天器姿态镇定的问题,提出了一种基于模态观测器的反步控制设计方法。
结合上述研究,本文利用反步法设计了一种自适应跟踪控制器,确保模块进入充电区域时接收装置实现对能量源模块的指向。首先介绍了分离模块航天器无线能量传输的方式,根据模块的实际特点选取了描述其姿态的数学模型。然后推导出模块姿态误差动力学方程并针对此方程设计了反步控制器,考虑到模块转动惯量的不确定性,设计了自适应律对其进行在线估计,最后的仿真结果表明了该控制器的有效性。
1 无线能量传输方式
无线能量传输技术是分离模块航天器关键技术之一。针对传统微波等方法传输效率低的问题,文献[4-5]提出一种聚光传输方法。聚光方式能量传输过程如图1所示。装有空间反射镜的能量源模块可以实现对日指向调整,以保证直径最大的主反射镜朝向太阳。主反射镜与小直径反射镜配合,最终将光束传递到直径0.1 m的小反射镜上,在该过程中能量聚焦100倍左右,小反射镜校准,将光束射向任务模块。该方案避免了太阳光到直流以及直流到射频的转换损失,整体效率在20%~25%。
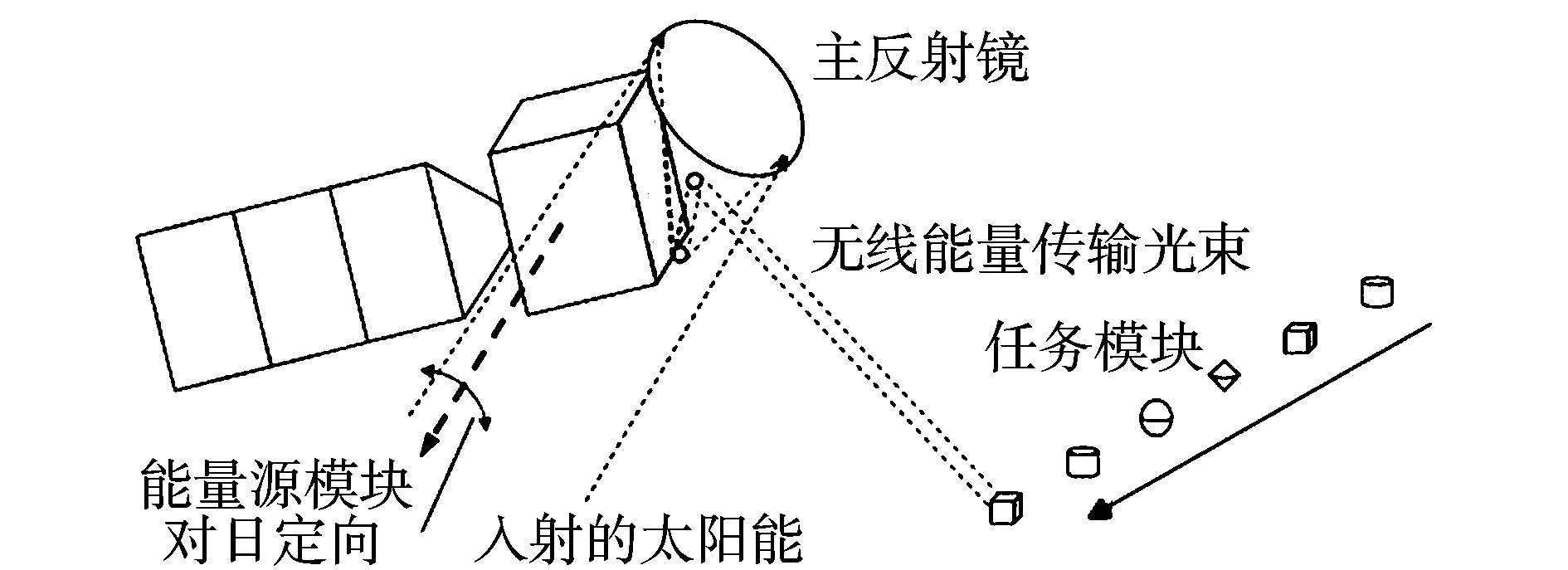
图1 无线能量传输示意图Fig.1 Wireless power transmission diagram
在接收端,任务模块需要安装一个低成本的热力发电机以接收高密度太阳光(见图2),将其转换成电能以对载荷和平台供电。图3为典型的模块航天器编队飞行方案,利用小反射镜的配合在相对轨道上形成一个充电区域,一旦任务模块进入该充电区域,就需要调整姿态使得发电机接收面对准能量源模块以接收能量。
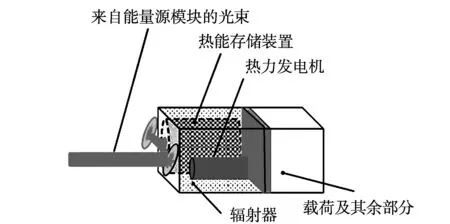
图2 能量接收装置示意图Fig.2 Energy receiving device diagram
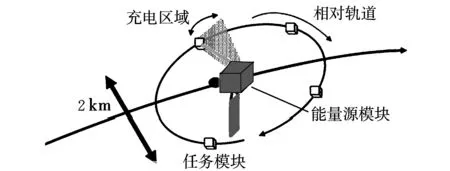
图3 典型的编队队形Fig.3 Typical formation
2 模块姿态数学模型
描述航天器姿态的参数有多种形式,修正的罗德里格斯参数(MRP)没有冗余参数,同时可以减小奇异的影响,因此本文采用MRP描述模块的姿态。其定义如下[11]:
(1)
式中,e为欧拉轴;Φ为欧拉转角。考虑分离模块航天器中各模块不需要安装太阳帆板,因而使用经典的欧拉转动方程描述模块的姿态动力学,其姿态动力学和运动学方程为:
(2)
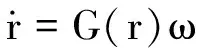
(3)
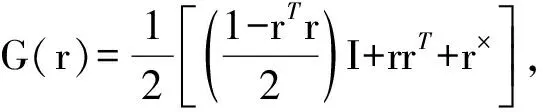
(4)
设模块的期望姿态为rd,期望角速度为ωd,则定义姿态误差为re=r-rd,姿态角速度误差为ωe=ω-Cωd,C为姿态变换的方向余弦矩阵,将其代入式(2)得到误差动力学和运动学方程为:
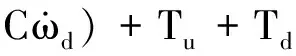
(5)

(6)
假设1:由于有效载荷的旋转等因素导致模块转动惯量得不到精确值,考虑J为未知的常量并假设0≤‖J‖≤cJ,模块受到的干扰主要有太阳光压力矩等,假设干扰有界为0≤‖Td‖2≤d,其中cJ,d∈R为未知常数。
3 指向跟踪控制器设计
3.1 期望姿态解算

对于任务模块,设R为目标线方向单位向量,则R可以表示为[cosβcosα,cosβsinα,sinβ]T,欧拉轴e垂直于x和R所在平面,则e和Φ为:
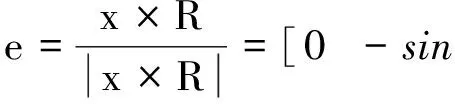
(7)
Φ=arccos(cosαcosβ)
(8)

图4 期望姿态解算示意图Fig.4 Desired attitude calculation eiagram
3.2 自适应反步控制器设计
引理1[12]:若正定函数V(t)满足如下不等式:
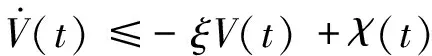
(9)
式中,ξ为正常数;对∀t>0,χ(t)>0。如果χ(t)为常数,则系统是全局一致有界稳定的。
由式(5)、式(6)可知,模块航天器误差动力学系统是级联系统,按照反步法步骤定义新的变量如下:
x1=re
(10)
x2=ωe-ωev
(11)
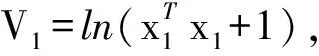
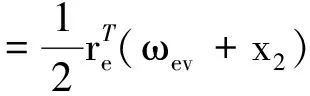
(12)
为了方便应用Lyapunov稳定性理论,这里选取ωev=-λre,其中λ为正常数,将其代入式(12)得:
(13)
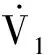
(14)
因此得到re渐近收敛于零,从而x2=0成为下一步设计的目标。考虑转动惯量的不确定性,应对其进行自适应在线估计,对x2求导并且将姿态误差动力学方程(5)代入得到:
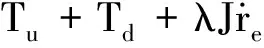
=-ω×Jω+Jε+Tu+Td
(15)
其中:
(16)
为了化简式(15),定义如下矩阵和惯量参数:
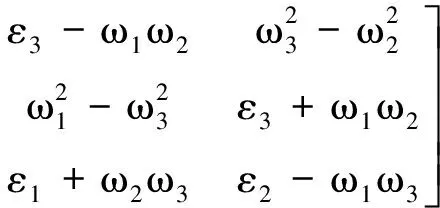
(17)
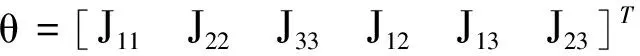
(18)
则式(15)改写成如下形式:
(19)
模块转动惯量的不确定性集中体现在参数θ上,因此需对θ进行自适应在线估计,设计其自适应更新律为:
(20)

(21)
对式(21)求导并将式(13)、式(19)、式(20)代入得到:

(22)
设计如下控制律:
(23)
式中,ρ和γ均为正常数;γx2是为了补偿式(2)中的干扰项而设计。将式(23)代入式(22)中得:
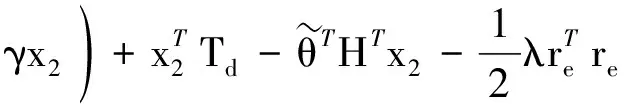
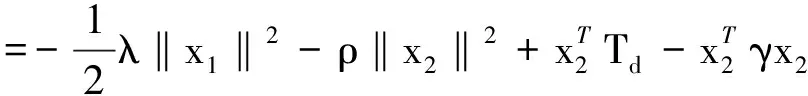
(24)
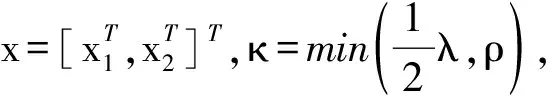
(25)
利用式(25)并结合假设1,式(24)转化为:
(26)
由式(21)可得:
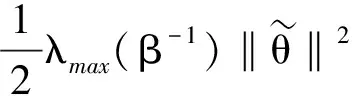
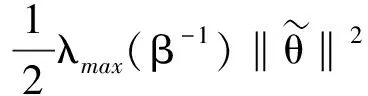
(27)

V2≤τ‖x‖2+μ
(28)
(29)
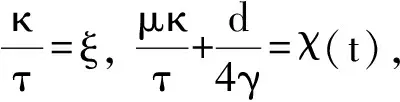
(30)
根据引理1知,该系统是全局一致有界稳定的。
4 仿真验证
为了验证式(23)的有效性,基于Simulink对模块跟踪控制进行仿真。假设模块的转动惯量为:


仿真结果如图5~图7所示。从仿真结果可以看出,模块航天器在4 s左右跟踪时变期望信号,表明该控制器实现了对模块转动惯量的估计,并且有效抑制了外部干扰力矩对模块的影响。
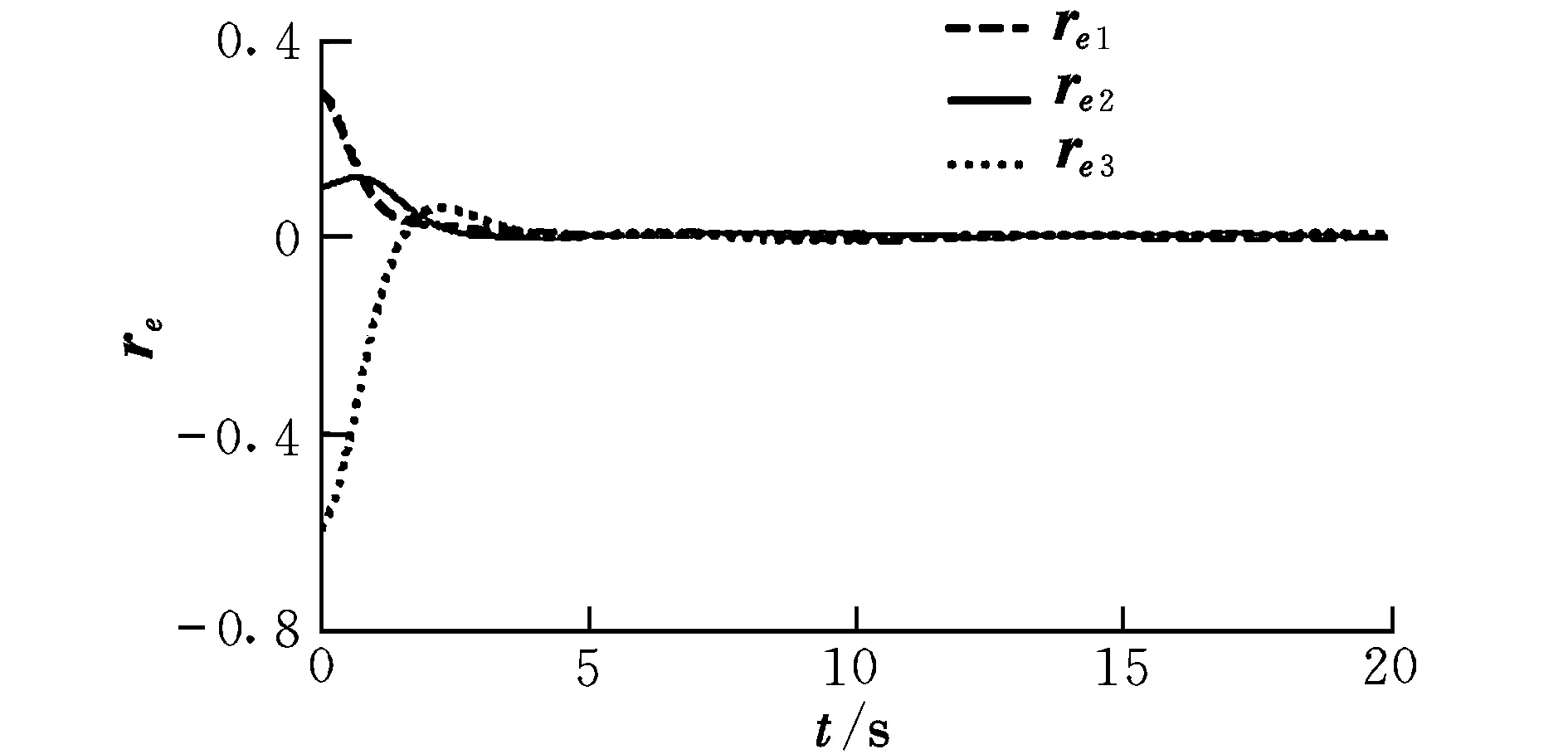
图5 姿态跟踪过程中MRP误差曲线Fig.5 MRP error during attitude tracking
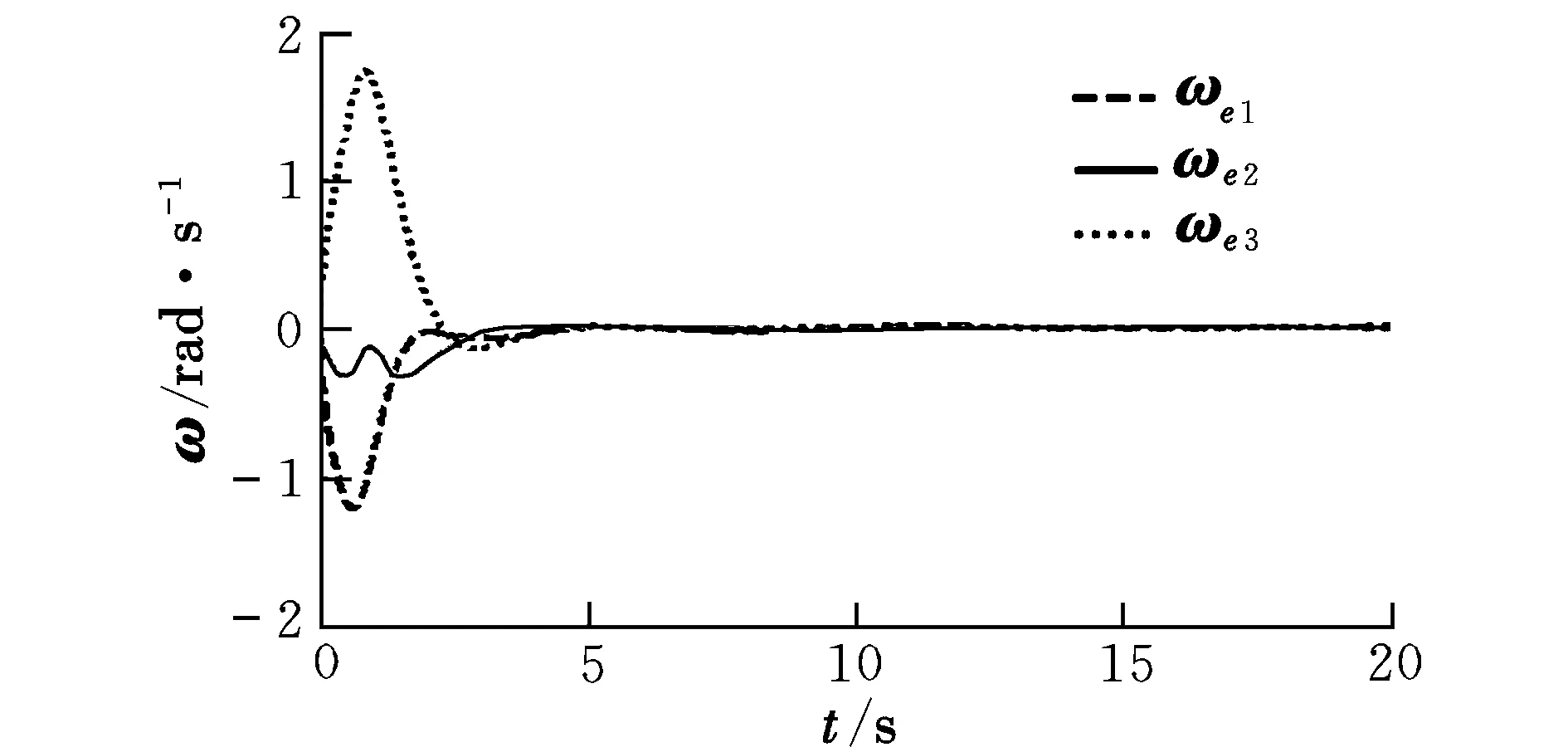
图6 姿态跟踪过程中角速度误差曲线Fig.6 Angular velocity error during attitude tracking
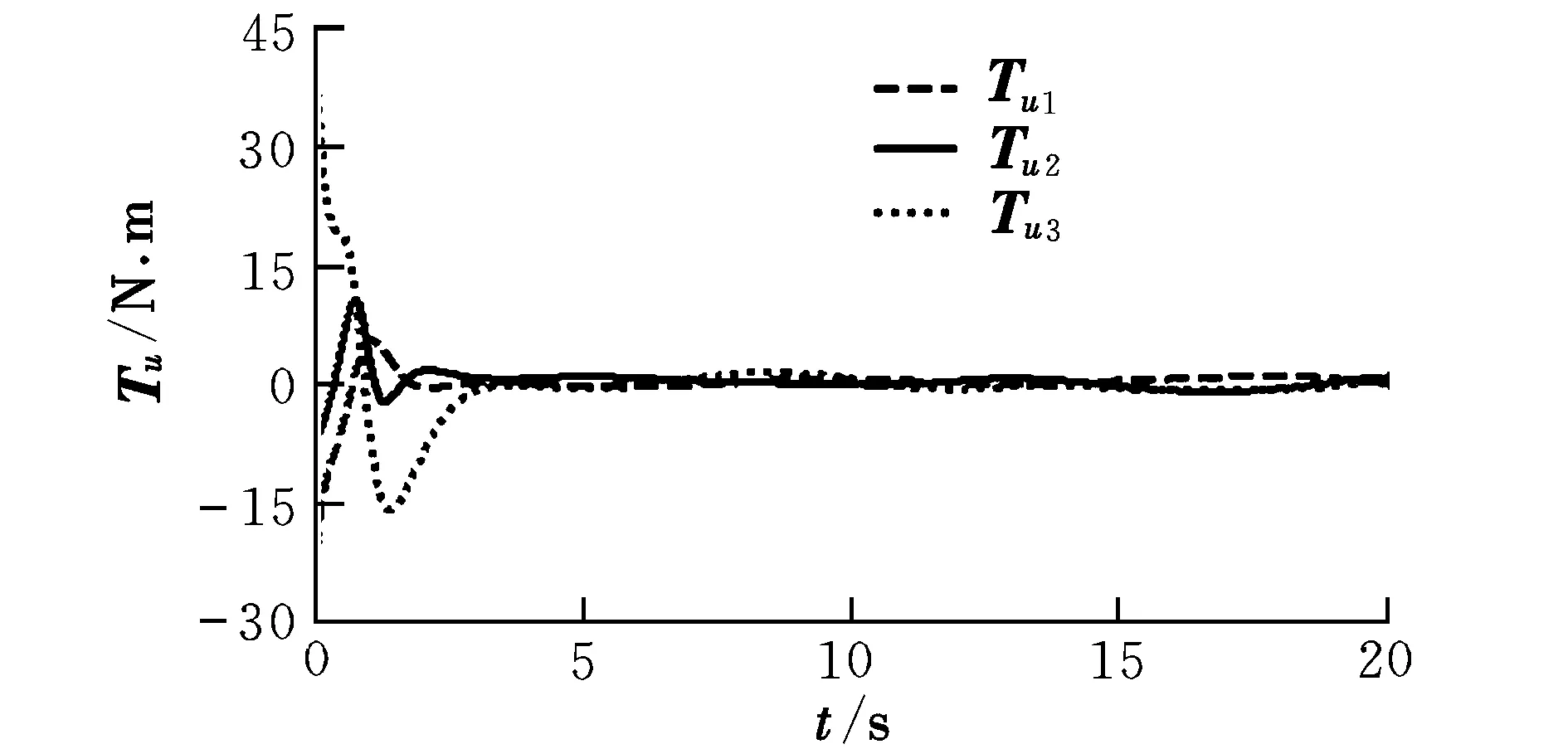
图7 姿态跟踪过程中控制力矩曲线Fig 7 Control moment during attitude tracking
5 结束语
本文利用反步法设计了一种模块航天器自适应姿态指向跟踪控制器,确保模块进入充电区域时接收装置可以指向能量源模块以获取能量。考虑到模块转动惯量的不确定性,设计了自适应律对其进行在线估计,同时设计了非线性阻尼项补偿外部干扰力矩。最后的仿真结果表明,该控制器可以实现任务模块对能量源模块的指向跟踪。本文设计的控制器结构简单,对外界干扰具有一定的鲁棒性,为模块航天器姿态跟踪控制器的设计提供了参考。
参考文献:
[1] 胡敏,曾国强.分离模块集群航天器发展概况[J].装备指挥技术学院学报,2011,22(4):62-65.
[2] 刘豪,梁巍.美国国防高级研究计划局F6项目发展研究[J].航天器工程,2010,19(2):93-99.
[3] O’Neill M G,Yue H K.Comparing and optimizing the DARPA system F6 program value-centric design methodologies[R].AIAA-2010-8828,2010.
[4] Turner A E.In-space power transfer using concentrated,unconverted sunlight[C]//International Energy Conversion Engineering Conference.Denver:AIAA,2009:4537.
[5] Turner A E.Power transfer for formation flying spacecraft[R].AIAA-2006-7493,2006.
[6] 王冬霞,石恒,贾英宏,等.航天器姿态指向跟踪的一种自适应滑模控制方法[J].空间控制技术与应用,2010,36(6):22-26.
[7] 高有涛,陆宇平,徐波.卫星编队飞行的探测目标指向动力学与控制方法研究[J].宇航学报,2009,30(3):1001-1005.
[8] 马广富,张海博,胡庆雷.基于反步法的主从航天器相对姿态控制[J].控制理论与应用,2012,29(6):798-802.
[9] 赵学民.反步自适应滑模变结构的小卫星姿态鲁棒容错控制[J].计算机工程与应用,2012,48(19):220-224.
[10] 王翔宇,丁世宏,李世华.基于反步法的挠性航天器姿态镇定[J].航空学报,2011,32(8):1512-1523.
[11] Schaub H,Junkins J L.Stereographic orientation parameters for attitude dynamics: a generalization of the Rodrigues parameters[J].Jouranl of the Astronautical Sciences,1996,44(1): 1-19.
[12] Qu Z H,Dawson D M,Lim S Y,et al.A new class of robust control law for tracking of robots[J].The International Journal of Robotics Research,1994,13(4):355-363.

