倾转旋翼机建模及其配平计算
王奇, 吴文海, 曲志刚, 何健
(海军航空工程学院 青岛分院, 山东 青岛 266041)
0 引言
倾转旋翼机综合了直升机垂直起降与螺旋桨飞机高速巡航的能力,因而,在过去几十年里,倾转旋翼机研究获得了各国航空界的广泛关注[1-3]。文献[4-5]建立了倾转旋翼机三自由度运动模型,但模型中旋翼动力学简化过多;文献[6]建立了较为完整的六自由度运动模型,但对桨叶惯性力处理过度,其余气动部件(尤其是机翼)又过于简化,未考虑短舱动态以及气动部件间的相互气动干扰;文献[7]建立了倾转旋翼机模型,该模型适合进行飞行性能计算、飞行仿真与本体稳定性分析;杨喜立等[8]建立的模型侧重于旋翼动力学,未对其他气动部件及干扰特性进行深入分析;文献[9]针对倾转旋翼机过渡模式下的气动力干扰、重心变化、陀螺力矩对机体干扰等动力学问题,建立了较为完善的基本动力学模型,但未对相关力与力矩产生机理及控制面作用进行分析。
为便于进行飞行控制设计与仿真,对于短舱倾转动态、模式转换引起的机体结构参数变化、旋翼与各气动部件间的相互干扰等特性,在模型中需要给予考虑。而旋翼模型可适当简化,以便于控制量的分离与计算负荷的减少。
1 基本动力学方程
倾转旋翼机具有直升机与飞机的运动特性,详细描述其运动需要综合直升机与飞机相关坐标系,两种旋翼系统相关坐标系定义一致,研究中用到的坐标系为:地理坐标系、机体坐标系、气流坐标系、短舱坐标系、桨轴坐标系与桨叶坐标系等。
1.1 平动动力学方程
倾转旋翼机动力学最大特点是具有短舱动力学特性,因此,在质心运动方程中需要考虑短舱动态的影响,可表示为:
fB=(m-mN)aB+mNaN
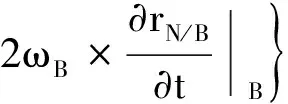
(1)
式中,vB=[u,v,w]T;ωB=[p,q,r]T;m为飞行器总质量;mN为短舱质量;rN/B为短舱质心相对于机体质心的矢径;fB为飞行器所受合外力在机体坐标系内的矢量,其表达式为:
=f0+f(u)
(2)

1.2 转动动力学方程
考虑短舱动态的转动动力学为:
ωB×(IBωB)+mNωB×(rN/B×vB)+
ωB×(IN/B×ωB)
(3)
式中,βM为短舱角(直升机模式为0°);IN/B为短舱相对于质心的惯性矩阵;mB=[L,M,N]T由各个气动部件产生的力矩叠加而成,并可拆分成常量与可控部分:
=m0+m(u)
(4)
2 多体部件模型
2.1 机身/机翼动力学
2.1.1 机身动力学
机身所受气动力与气动力矩是倾转旋翼机气动迎角与侧滑角的函数,由风洞试验得出,可表达为:
AF=qFfAF(αF,βF)
(5)
式中,AF为气动力或气动力矩;qF为机身处的动压值。将气动力与气动力矩转换至机体坐标系内,得到机身对机体的作用力与力矩:
(6)

2.1.2 机翼动力学
倾转旋翼机的机翼作用面积分为两部分:一是受旋翼气流影响的机翼部分,其面积随短舱倾转而发生变化;另一个是不受旋翼气流影响的自由流区。旋翼气流影响下的机翼面积可由下式简化计算[5]:
(7)
(8)
式中,Sssmax=2ηssRcW,ηss<1为修正系数;in=90°-βM;umax为临界速度值;a,b为匹配试验数据而选取的适当数值。
在机体坐标系内,机翼对机体总的力与力矩为:
(9)
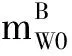
2.2 旋翼动力学方程
以右侧旋翼为研究对象,采用叶素理论,考虑短舱倾转导致桨叶陀螺力矩,得到桨轴坐标系内旋翼的拉力系数为:
(10)
旋翼后向力与侧向力为:
(11)
式中,Fy为平行桨盘力;FR=ρU2cCL/2。
左、右侧旋翼挥舞产生的俯仰力矩大小相同、方向一致,其大小为:
cosψHdFzdψH
(12)
将旋翼力和力矩转换到体轴系为:
(13)
2.3 平尾模型
在旋翼流影响下,平尾气流速度为:
(14)
通过此气流速度可以求出平尾的迎角αH与侧滑角βH。则平尾的升力和阻力为:
(15)
转换到机体坐标系,得到平尾对机体的力及力矩为:
(16)
2.4 垂尾模型
垂尾的侧力与阻力为:
(17)
得到垂尾对机体的力及力矩为:
(18)
3 计算结果及分析
将式(1)与式(3)进行配平计算,航迹量不参与配平计算(如ψ=0°,χ=0°),并令方程组中角速度值与各参数导数项为零。此时未知数(状态:u,v,w,φ,θ;输入:δa,δe,δr,θ0,θ1s,θ0d,θ1sd)多于方程数,采用文献[11]给出的角度公式进行补充:
(19)
式中,s*与c*分别表示sin*与cos*。由上式引入新未知量φV,由于空速V由外界指令输入,最终未知数为12个,方程组为9个。短舱角由外部指令赋值,期望配平飞行状态为定常水平直线飞行(γ=0°),所用数据来自文献[12]。
3.1 未知数多于方程组数的配平
采用Levenberg-Marquardt算法进行未知数多于方程组数的配平计算。倾转旋翼机在不同短舱角下保持定直平飞状态的纵向控制量如图1所示。在小短舱角(0~15°)时,飞行器状态与直升机类似,即总距随前飞速度增大先减小再增大;随短舱前倾与机翼作用的提高,空速越大所需总距也越大。图中给出了与GTRS模型配平结果的对比。由图1可知,在小短舱角(βM<15°)、低空速条件下,升降舵作用小偏度不大;随短舱倾角增大(βM<45°)、空速增加,舵面经历先增加再回收减小过程;大于45°的短舱角不再有上述过程。在相同短舱角、低速下,纵向周期变距随空速增大提供低头力矩的操纵量增大,在空速大于临界速度之后,气动面效率增大,旋翼纵向周期变距操纵逐渐减小。在整个配平结果中,升降舵偏度没有超出饱和值±20°,纵向周期变距小于±10°。
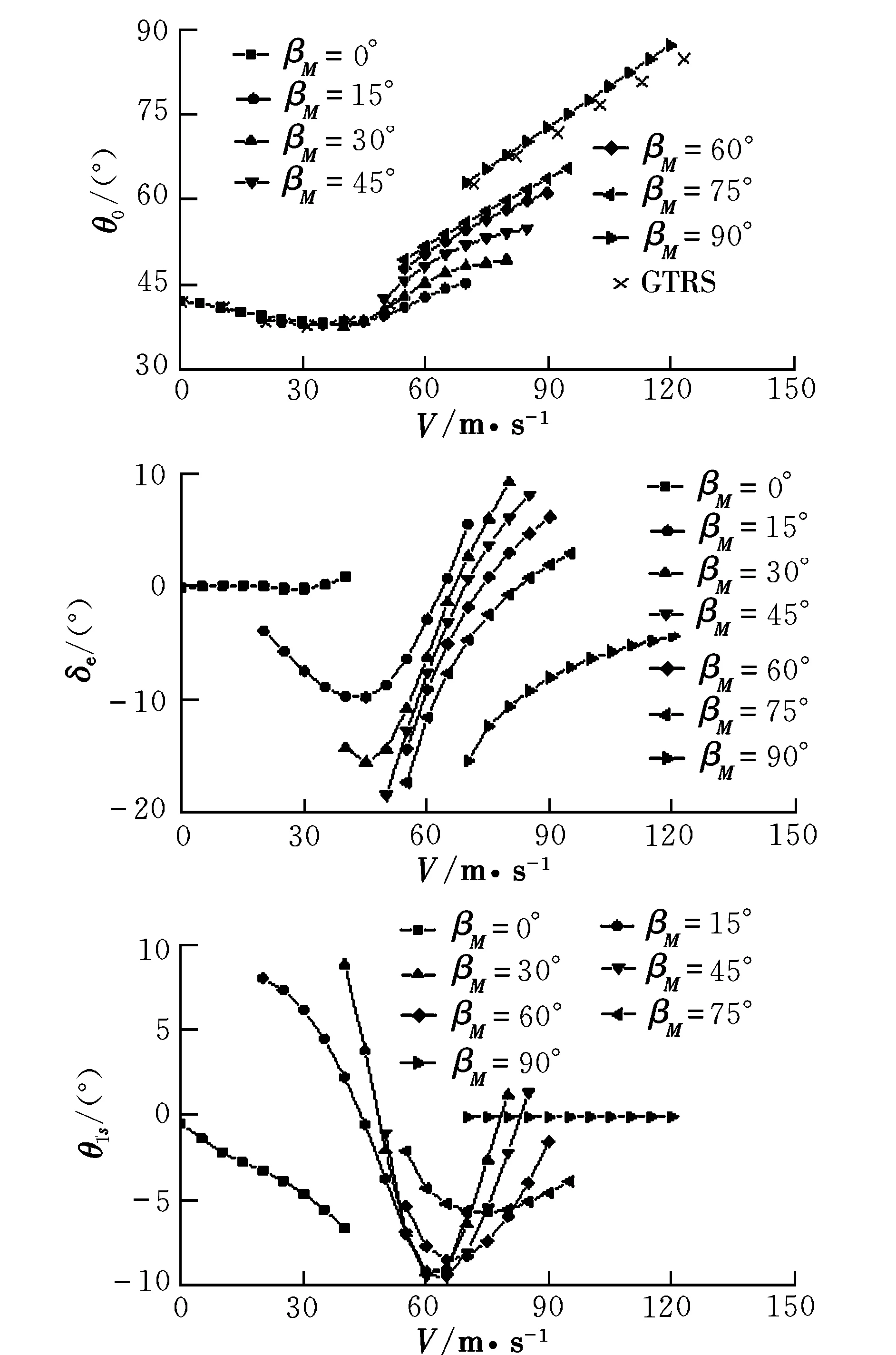
图1 不同βM下的平飞控制量Fig.1 Level flight controls at different βM
3.2 控制混合下的配平
控制混合的概念与控制分配思想相似,是将三轴姿态的控制指令按一定规律分配到冗余的操纵舵面上。控制混合通过驾驶杆与脚蹬将旋翼和空气舵面控制进行结合,其关联系数随短舱角倾转而发生变化。在开环情况下,旋翼总距和纵向周期变距与杆和脚蹬操纵的关系如下:
(20)
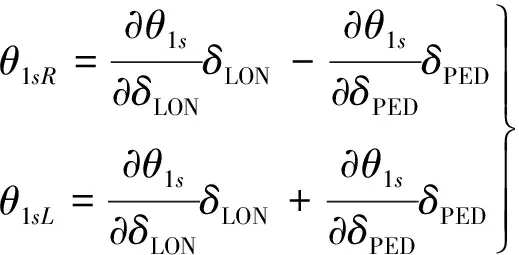
(21)
式中,δCOL,δLAT,δLON与δPED分别为总距杆、横向杆、纵向杆与脚蹬操纵量。由上式得到旋翼操纵量与气动舵面间的关系为:
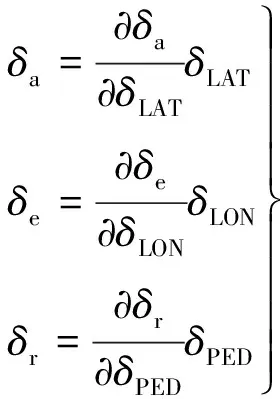
(22)
式(22)的补充使得未知数与方程组数相同,可采用常用算法进行配平计算,结果如图2所示。由图2可知,在短舱角为0°时,纵向操纵为正向推杆,此过程中俯仰角不断减小,旋翼拉力轴随之不断前倾,随气动舵面效率的提高,所需杆量有适量回复;其他短舱角下,随速度的增大,杆量都是由后拉变为前推,姿态角也是由大变小;βM=0°,45°,90°的配平姿态角与GTRS结果相差不大。

图2 控制混合下配平纵向杆与俯仰角Fig.2 Trimmed longitudinal controls and pitch angles by control mixing
4 结论
(1)建立了倾转旋翼机基本动力学运动方程,考虑了短舱倾转对运动方程的影响。较为完整地建立了各气动部件模型,满足计算仿真实时性与准确性的要求。
(2)采用Levenberg-Marquardt计算方法,对所建模型进行了未知量多于方程组数下的配平计算,得到了与倾转旋翼机特性相符的计算结果。
(3)采用控制混合进行了另一种方式的配平计算,得到了与上述方法相同的结果。
参考文献:
[1] Foster M.The future evolution of the tiltrotor[R].AIAA-2003-2652,2003.
[2] Alli P,Nannoni F,Cicalè M.Erica:the european tiltrotor design and critical technology projects[R].AIAA-2003-2515,2003.
[3] Choi S,Kang Y,Chang S,et al.Development and conversion flight test of a small tiltrotor unmanned aerial vehicle[J].Journal of Aircraft,2010,47(2):730-732.
[4] Carlson E B,Zhao Y J.Optimal city-center takeoff operation of tiltrotor aircraft in one engine failure[J].Journal of Aerospace Engineering,2004,17(1):26-39.
[5] Carlson E B,Zhao Y J.Prediction of tiltrotor height-velocity diagrams using optimal control theory[J].Journal of Aircraft,2003,40(5):896-905.
[6] Kleinhesselink K M.Stability and control modeling of tiltrotor aircraft[D].College Park:University of Maryland,2007.
[7] Miller M,Narkiewicz J.Tiltrotor modelling for simulation in various flight conditions[J].Journal of Theoretical and Applied Mechanics,2006,44(4):881-906.
[8] 杨喜立,朱纪洪,黄兴李,等.倾转旋翼飞机建模与仿真[J].航空学报,2006,27(4):584-587.
[9] Li H X,Qu X J,Wang W J.Multi-body motion modeling and simulation for tilt rotor aircraft[J].Chinese Journal of Aeronautics,2010,23(4):415-422.
[10] 肖业伦.航空航天器运动的建模——飞行动力学的理论基础[M].北京:北京航空航天大学出版社,2003:19-23.
[11] Gordon L J.Principles of helicopter aerodynamics [M].2nd ed.New York:Cambridge University Press,2006:95-96.
[12] Harendra P B,Joglekar M J,Gaffey T M,et al.A mathematical model for real time-flight simulation of the Bell model 301 tilt rotor research aircraft model 301[R].Bell Helicopter Company Report No.301-099-001,1973.

