时变双曲型发展方程的强解*
汤小燕,罗东升
(遵义师范学院)
1 预备知识
Banach空间X中的时变双曲型发展方程的初值问题:

其中无界闭稠定线性算子族{A(t)|t∈[0,T]}满足双曲型假设.Pazy,Kato等人[2-4]讨论了算子族{A(t)|t∈[0,T]}满足较强假设条件下Y值解和古典解的存在唯一性,然后又在较弱条件下引进温和解,给出温和解存在的一些充分条件.在该文中引进介于温和解与Y值解之间的广义解——强解,给出强解存在的充分条件.
设X和Y是Banach空间,其范数分别是‖·‖,‖·‖Y,Y是X的稠子空间且连续嵌入到X.对任意t∈ [0,T],A(t)是X上C0半群{St(s),s≥0}的无穷小生成元.双曲型假设(H)*:
(H1):{A(t)|t∈[0,T]}是稳定族,其稳定系数是M,ω,
(H2):对任意t∈[0,T],空间Y是A(t)-容许,(t)是A(t)在Y中的部分,算子族(t)|t∈[0,T]}在Y中是稳定的,其稳定系数为,,
(H3):对t∈[0,T],D(A(t))⊃Y,且A(·)∈C([0,T],B(Y,X)).
定理1.1 (见文献[2]推论 5.2.27)如果Y是自反Banach空间,算子族{A(t)|t∈[0,T]}满足假设(H)*,那么在X上存在唯一的发展系统{U(t,s),0 ≤s≤t≤T},满足(E1)、(E2)、(E3),且
(i)任意 0 ≤s≤t≤T,U(t,s)Y⊆Y,‖U(t,s)‖B(Y)≤e(t-s)同时U(t,s)是弱连续的.
(ii)任意ξ∈Y,0≤s<t≤T=A(t)U(t,s)ξa.e.,且是弱连续的.
定义1.2 函数x:[0,T]→X称为初值问题(1)的强解,如果:
(i)x∈L1([0,T],Y)∩C([0,T],X).
(ii)x在[0,T]上几乎处处可微,dxdt∈

2 时变双曲型发展方程的强解
情形1:当f=0时,考虑问题:

的强解.
命题2.1 如果Y是自反Banach空间,算子族{A(t)|t∈[0,T]}满足假设(H)*,那么对任意x0∈Y,初值问题(LE)1有唯一的强解,且
证明U(·,0)x0∈C([0,T],X).由命题1.1 中(i),对任意0 ≤s≤t≤T,U(t,s)Y⊂Y,且U(·,0)x0在Y空间中是弱连续的(见文献[1]),函数x是强可测的,且

故x∈L'([0,T]),Y).
由定义1.1 中的(ii),函数x(·)=U(·,0)x0是几乎处处可微的,且
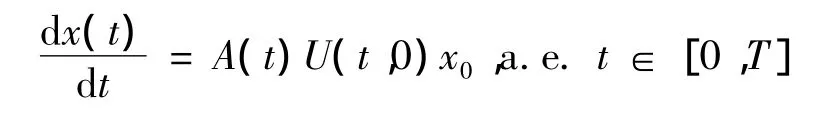
由假设(H)*知.由发展系统的唯一性,问题(LE)1有唯一的强解x.情形2 当f=f(t)时,考虑问题:

的强解.
命题2.2 如果Y是自反Banach空间,算子族{A(t)|t∈[0,T]}满足假设(H)*,对任意f∈L1([0,T],Y),x0∈Y,那么初值问题(LE)2存在唯一的强解x,且

证明 首先由温和解的定义,易证问题(LE)2有唯一的温和解x∈C([0,T],X).其次,由命题2.1,U(t,0)x0,t∈[0,T]是问题(LE)2对应齐次问题的强解.下面只需证明

是问题(LE)2对应于初值为0的强解.因f∈L1([0,T],Y),故z在Y中是可测的.又因

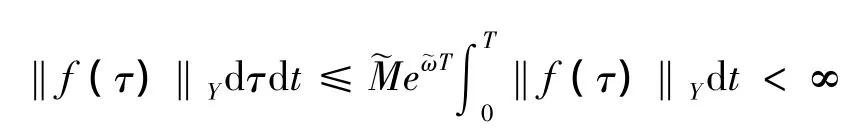
从而z∈L1([0,T],Y).由假设(H)*和f∈L1([0,T],Y),有

即A(·)f(·)∈L1([0,T],X).
对任意充分小的h>0,有

用定义1.1中(LE2)和(ii),对式子(2)和式子(3)取极限,得

即z几乎处处可微,且z'(·)∈L1([0,T],X).这就意味着

t∈[0,T]是问题(LE)2的强解.
情形3 考虑问题(1)的强解.
假设[F1]:
(1)f:[0,T]×Y→Y是一个映射,对任意ξ∈Y,f(·,ξ)∈C([0,T],Y),
(2)存在正常数L>0,对任意t∈[0,T],ξ,η∈Y,使得

命题2.3 如果Y是自反Banach空间,算子族{A(t)|t∈[0,T]}满足假设(H)*,假设[F1]成立.那么对任意x0∈Y,初值问题(1)在[0,T]上有唯一的强解x.
证明 由命题1.1中(i)知,存在常数存在M>0,使得对所有0≤s≤t≤T,有
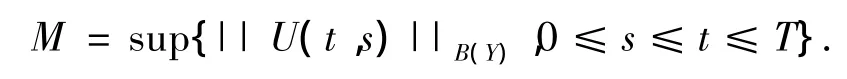
对固定的x0∈Y,在空间L1([0,T],Y)中定义映射F:

设x∈L1([0,T],Y),则

故,F:L1([0,T],Y)→L1([0,T],Y).
对任意u,v∈L1([0,T],Y),有
当n=1时,

当n=2时,

当n=3时,

重复上述过程,有

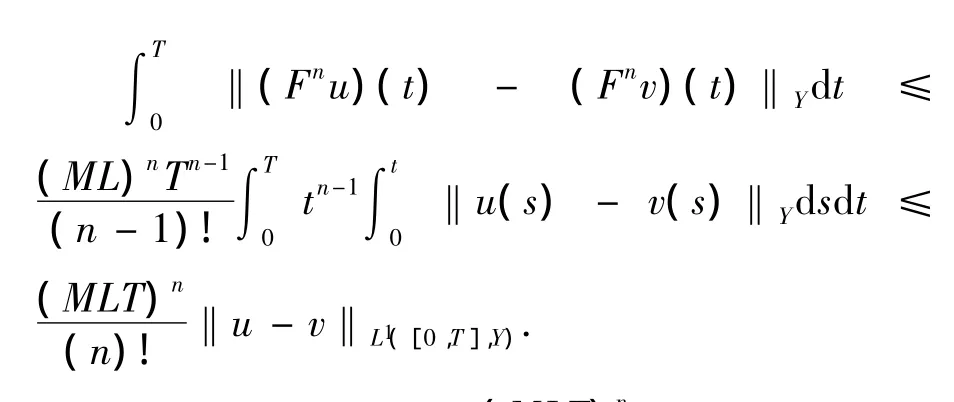
于是存在足够大的n,使得,从而Fn是L1([0,T],Y)的压缩映射,故F在L1([0,T],Y)中有唯一的不动点,且

由发展系统在空间X中的性质,可知
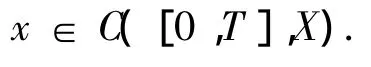
下证,x满足问题(1).对任意的t∈[0,T],令

由假设[F1]成立知,在空间Y中g是[0,T]上的可测函数,又

根据命题2.2,初值问题

存在唯一的强解v∈L1([0,T],Y)∩C([0,T],X),且对任意t∈[0,T],有

所以x是问题(1)在[0,T]上的强解.
3 结束语
由于时变双曲型发展方程的发展系统的性质没有抛物型发展系统的性质好,相应的假设比较繁杂,该文主要引进了自反Banach空间中发展方程的强解,并给出了存在定理的证明.这为进一步研究时变双曲型发展方程解的性质打下基础.
[1] 定光桂.巴拿赫空间引论.北京:科学出版社,1984.
[2] Pazy A.Semigroups of Linear Operators and Applications to Partial Differential Equations.New York,Springer-Verlag Inc,1983.
[3] Herbert Amann.Linear and quasilinear parabolic problems.Berlin,1995.
[4] Kato T.Abstract evolution equations of“hyperbolic”type.J Fac Sci Univ Tokyo,1970,25:241-258.

