关于多元函数极限的一点注记

蔡俊亮

(北京师范大学数学科学学院数学与复杂系统教育部重点实验室，北京100875)

1 引 言

众所周知，微积分教学工作已从过去的精英教学模式逐步转化为当前大众化教学模式. 即以前仅作为数学专业基础课的微积分教材，现已逐步变为诸如数学分析基础(讲义,原理),高等数学(引论,基础,教程)及大学数学等不同形式渗透到大学教学各专业领域中,作为必修课或选修课. 而与此相关的教材也应运而生，并且种类繁多[1-10]. 显然,作为这类教材内容的一个重要概念,极限,必须要简单明了、准确无误,更不能含糊不清甚至出现自相矛盾的现象. 然而，据作者多年教学经验，并经认真思考与研究后发现:一元函数极限概念相对标准,但多元情形较乱,甚至自相矛盾.本文试图就此问题展开研究,并以一元函数极限的概念为标准，给出多元情形一个标准定义.

2 有关极限的概念

通常,在给出函数、极限和连续的概念之前,先要介绍一些相关的集合概念.这些概念较简单,也易理解,但其表述方式有差异.为统一起见,尽量用标准语言和记号表述n-维空间的一些集合和函数的概念:全体实数集,自然数集(含0),整数集,正整数集+,有理数集等.

对于n∈+,n-维空间中全体点集称为全集,记为n,即n={(x1,x2,…,xn)|∀x1,x2,…,xn∈}. 空集记为∅.设x=(x1,x2,…,xn)，y=(y1,y2,…,yn)∈n, 则x和y两点之间的距离

具有某种性质P的全体点为n的一个子集,记为E={x|x∈n.满足性质P}⊆n;Ec=nE称为点集E的补集:如∅c=n,(n)c=∅. 另外, 点集有有限集,无限集等.

设x0∈n,δ为正数, 以x0为中心,δ为半径的开球称为点x0的δ-邻域, 记为

Uδ(x0)=U(x0,δ)={x|x-x0|<δ}.

点集U°δ(x0)=U°(x0,δ)={x|0<|x-x0|<δ}称为x0的去心δ-邻域.

设x0∈E⊆n. 若存在δ>0,使U(x0,δ)⊆E,则称x0为E的内点;E的补集Ec的内点称为E的外点;否则称为E的界点.E的界点的集合称为E的边界，记为∂E.点集E⊆n，若存在某个正数M使得E⊆U(O,M),其中O为n-维空间的坐标原点,则称E为有界点集. 否则无界点集. 若非空点集E的每个点都是E的内点,则称E为开集. 若有界点集E的边界∂E⊆E,则称E为闭集.一般地,点集E⊆n的闭集为⊆n.对非空点集Ω⊆n, 若其中任意两点均可用Ω中的折线连接起来, 则称Ω为连通集,简称区域；连通的开集称为开区域；连通的闭集称为闭区域.闭区域总有界.

设x0∈E⊆n,若存在δ>0使得U°(x0,δ)∩E=∅，则称x0为E的孤点; 若任意δ>0,使得U°(x0,δ)∩E≠∅，则称x0为E的聚点.

注意：点集E的孤点是界点，但非聚点；点集E的内点为聚点，但聚点并非内点；点集E的界点和聚点未必属于E.

n-元函数的定义设非空点集Ω⊆n. 若对每个点x∈Ω,变量y都会按照一定的法则f唯一地确定中的一个值与其对应，则称变量y∈为变量x的n-元函数，记为y=f(x)， 其中点集Ω称为函数y=f(x)的定义域(实为点集)，x称为自变(向)量,y称为因变(向)量. 数集{y|y=f(x),x∈Ω}称为函数y=f(x)的值域, 简记为

f(Ω)={y|y=f(x),x∈Ω}⊆.

由此定义的函数为“单值”函数，对所谓的“多值”函数可将其化为若干单值函数去研究.

在一元函数微积分的教材中，与极限有关的概念和内容基本上是正确的，且比较统一. 虽然在不同教材中的表述形式略有不同，甚至有些不够准确，但并不存在原则上的错误[1-10].既然一元函数的这套极限的定义是公认的“标准”，那么多元情形就应当以一元函数的情形为“标准”进行相应的推广. 本文的目的就是要给出多(n-)元函数极限的一个标准定义.

3 多元函数极限定义中的问题

在此首先要对已经出现在各类微积分教材中的多元函数极限的定义进行一次普查,并对这些定义进行仔细分析和研究. 为简单计,我们主要对二元函数极限的定义进行普查. 纵览有关微积分教材(共调研了100余套教材,本文挑选了其中有代表性的10套作为参考文献)中的二元函数极限的定义，没有发现一个定义是标准的、全面的. 不妨具体分析如下：

在所研究的这些微积分教材中，无论二元函数极限的定义形式如何变化，但究其实质而言可归结为下面的三种形式：

二元函数极限定义3.1[1,2]设函数f(x,y)在点P0(x0,y0)处的某去心邻域U°(P0)内有定义，A为一个确定的常数. 若对任意给定的正数ε, 总存在正数δ,使得当P(x,y)∈U°(P0,δ)时，恒有|f(x,y)-A|<ε成立，则称函数f(x,y)在点P0处的极限存在(收敛)，该常数A称为函数f(x,y)在点P0处的极限. 否则，称函数f(x,y)在点P0处的极限不存在(发散).

定义3.1的缺陷是没有给出函数在区域界点处的极限定义，从而无法讨论函数在闭区域上的相关性质. 另外，按此定义许多函数的极限问题将无法讨论. 如，常见的函数

(1)

等在原点O(0,0)处的极限就没有定义,由于这些函数不满足定义的前提条件：函数“在U°(O)内有定义”.

二元函数极限定义3.2[3-7]设函数f(x,y)的定义域为D，P0(x0,y0)为D的一个聚点，A为一个确定的常数. 若对任意给定的正数ε, 总存在正数δ,使得当P(x,y)∈U°(P0,δ)∩D时，恒有|f(x,y)-A|<ε成立，则称函数f(x,y)在点P0处的极限存在(收敛)，该常数A称为函数f(x,y)在点P0处的极限. 否则，称函数f(x,y)在点P0处的极限不存在(发散).

定义3.2比定义3.1的适应范围要广泛一些. 如，按照定义3.2，(1)式中的4个函数在原点处的极限均存在且为0,即当(x,y)→(0,0)时，

(2)

但定义3.2也有漏洞，如考察函数

f(x,y)=1, (x,y)∈{(x,y)|x,y∈}=2.

(3)

定义3.3的适应范围更为广泛些. 这个定义虽然在某种程度上克服了前两个极限定义中的缺陷与不足，但此定义自相矛盾.因为它把函数在区域“界点”处的“极限”等同于函数在“内点”处的极限，正如在一元函数的情形把左、右极限等同于极限的错误一样. 我们认为这个定义对于一元函数情形是“不可兼容”的.

显然这是不合理的,因为和函数g(x,y)在整个平面上根本就没有定义.

以上论证表明:当前多元函数极限的定义均有缺陷和漏洞，需要修正.下面提供一种修改的建议，以供参考.

4 多元函数极限的标准化定义

当n-元函数f(x)在点x0处的极限不存在时，我们给出一种单侧极限的定义.

多(n-)元函数侧极限的定义4.2设函数f(x)在某区域Ω上有定义,A为一个常数,且x0∈∂Ω. 若对于任意的正数ε, 总存在正数δ，使得当x∈U°(x0,δ)∩Ω时,恒有|f(x)-A|<ε成立，则称n-元函数f(x)在点x0处的侧极限存在，该常数A称为函数f(x)在点x0处的侧极限, 记为

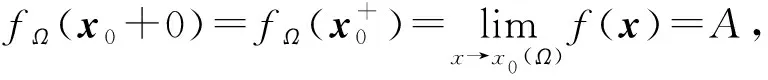
否则称f(x)在点x0处的侧极限不存在.

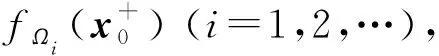
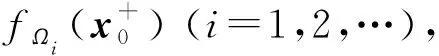
注意：(i)通常把多元函数的极限和侧极限统称为“极限”，具体的存在性须按定义考察.

(ii)无限远点处的极限可作类似定义，或用倒代换化为有限点情形讨论.

(iii)凡与极限有关的概念可作类似处理.

[参 考 文 献]

[1] 华罗庚. 高等数学引论[M]. 北京：高等教育出版社，2010.

[2] 欧阳光中. 数学分析[M]. 上海：复旦大学出版社，1993.

[3] 邝荣雨. 微积分学讲义[M]. 北京：北京师范大学出版社，2006.

[4] 张筑生. 数学分析讲义[M]. 北京：北京大学出版社，1990.

[5] 华东师范大学数学系. 数学分析[M]. 北京：高等教育出版社，2007.

[6] 马知恩，等. 工科数学分析基础[M]. 北京：高等教育出版社，2002.

[7] 同济大学数学教研室. 高等数学[M]. 4版. 北京：高等教育出版社，2005.

[8] 叶其孝，等. 实用数学手册[M]. 2版. 北京：科学出版社，2011.

[9] 邓东皋，等. 数学分析简明教程[M]. 北京：高等教育出版社，2000.

[10] 同济大学数学教研室. 高等数学[M]. 4版. 北京：高等教育出版社，2004.