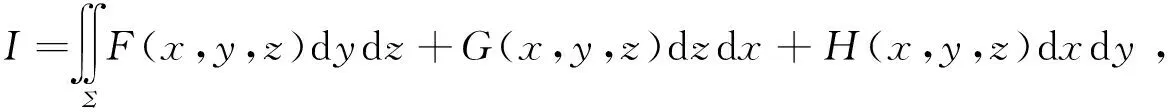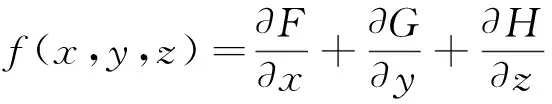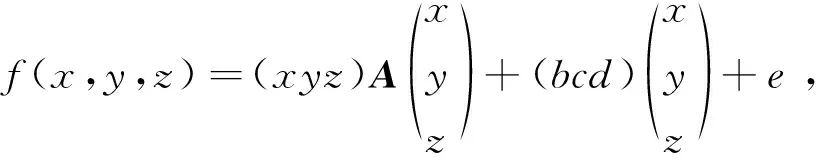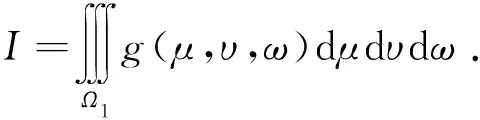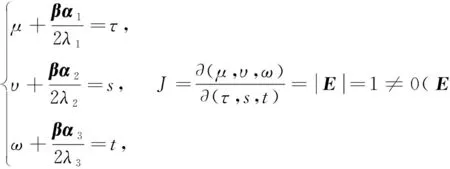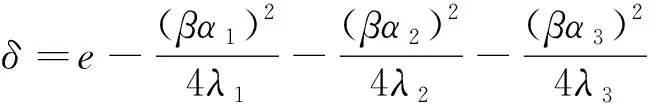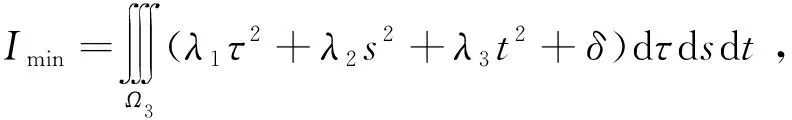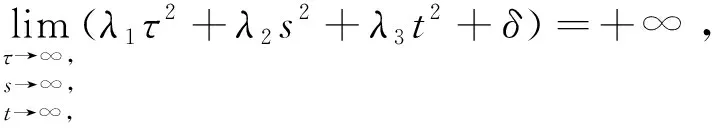关于一道全国大学生数学竞赛试题的思考
张立卓
(对外经济贸易大学统计学院,北京100029)
第五届(2013年)全国大学生数学竞赛预赛题:设Σ是一个光滑封闭曲面,方向朝外,给定第二型曲面积分
试确定曲面Σ,使积分I的值最小,并求该最小值.
解记Σ围成的立体为V,由高斯公式,
设椭球体V0:x2+2y2+3z2≤1,为使I的值最小,需讨论V与V0的位置关系:
(i) 若V在V0外,则在积分域V上,被积函数f(x,y,z)=3(x2+2y2+3z2-1)≥0.又f(x,y,z)不恒为0,
(ii) 若V=V1+V2,其中V1在V0外,
V2在V0内,在积分域V2上,被积函数f(x,y,z)=3(x2+2y2+3z2-1)≤0.又f(x,y,z)不恒为0,
(iii) 若V在V0内,
(iv) 若V=V0,
据三重积分性质,I4≤I3 作变换 积分域V0→V′0:μ2+υ2+ω2≤1,则依三重积分变换法及在球坐标系下三重积分的计算方法[1],有 下面考虑一般情形.设Σ是一个光滑封闭曲面,取外侧,给定第二型曲面积分 其中F(x,y,z),G(x,y,z),H(x,y,z)为3元3次实系数多项式,依高斯公式, 其中λ1,λ2,λ3为A的3个特征值.作正交变换 积分域Ω→Ω1.令正交矩阵P=(α1α2α3),其中α1,α2,α3为P的列向量,则 令β=(bcd),则 (1) 1.若A可逆,即A的3个特征值均不为零.不失一般性,设(1)式可化为 作变换 积分域Ω1→Ω2. (i) 当λ1>0,λ2>0,λ3>0,δ<0时,I有最小值. 但I没有最大值.这是因为 (ii) 当λ1>0,λ2>0,λ3>0,δ>0时,I没有最大(或最小)值.这是因为, 又令λ=max{λ1,λ2,λ3,δ},则λ>0,于是 取球体Ω′4:τ2+s2+t2≤ε2, 但I≠0,所以I没有最小值. (iii) 当λ1<0,λ2<0,λ3<0,δ>0时,I有最大值,但I没有最小值. (iv) 当λ1<0,λ2<0,λ3<0,δ<0时,I没有最小(或最大)值.证明方法同(ii). (v) 当λ1,λ2,λ3三者异号时,I没有最大(或最小)值.不妨设λ1>0,λ2>0,λ3<0,令椭圆柱体Ω6:λ1τ2+λ2s2≤1,t∈[t1,t2],则 (2) 对任意给定的正数M2,在(2)式中,固定t2,令t1充分大,注意λ3<0,则存在t′1,使 所以I没有最大值.又固定t1,令t2充分大,则存在t′2,使 所以I没有最小值. 2.若A不可逆,即A有零特征值.I没有最大(或最小)值.不妨设λ1>0,λ2>0,λ3=0,不失一般性,设(1)式可化为 作变换 积分域Ω1→Ω7,则积分 令椭圆柱体Ω8:λ1τ2+λ2s2≤1,t∈[t1,t2],则 与上述(v)同法可证,I没有最大(或最小)值. [参 考 文 献] [1] 同济大学数学系. 高等数学下册[M]. 6版. 北京:高等教育出版社,2007:229-232.