半桥型弧焊逆变电源的建模与仿真

常利建，田立欣，吕凯锋，金英博

（内蒙古工业大学电力学院，内蒙古呼和浩特 010080）

0 前言

弧焊逆变电源因其质量轻、体积小、动态响应范围广、控制性能好，以及焊接过程中便于实时控制等优点得到广泛的应用[1]。半桥电路结构简单，功率器件少，常应用于中小功率场合。本研究的弧焊逆变电源额定功率为4.2 kW，输出电流160 A，开关频率20 kHz。通过小信号建模以及设计PI控制器补偿，使弧焊逆变电源系统输出稳定，达到满意的效果。

1 半桥型弧焊逆变电源主电路的分析与动态建模[2]

半桥型弧焊逆变电源原理如图1所示。设开关器件IGBT1和IGBT2的栅极信号在一个周期内各有半周正偏，半周反偏，且二者互补。当IGBT1导通时，VDa由于承受正压而导通，经L、C3滤波后完成逆变。IGBT2导通时，同理。当VD1或VD2为通态时，变压器一次侧中贮藏的能量向直流侧反馈，反馈的能量暂时储存在直流侧电容器中，故而直流侧电容起缓冲无功的作用。

图1 半桥型弧焊逆变电源原理

1.1 工作模态1

当IGBT1导通时，一次电流由异名端流入，二次电流从异名端流出。当IGBT2导通时，一次电流由同名端流入，二次电流从同名端流出，方向一致，故可等效为同一工作模态，如图2所示。

图2 工作模态1原理

根据状态空间平均法，选电感电流、电容电压作为状态变量 x（t），ug为输入量 u（t），ig、uo为输出量y（t）。分析工作模态1，对二次侧回路列KVL方程

对电感L右侧节点列KCL方程

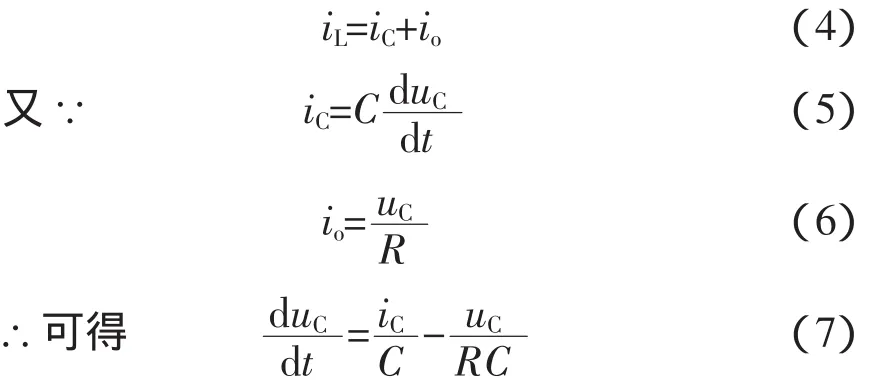
将式（3）和式（7）写成矩阵方程的形式：

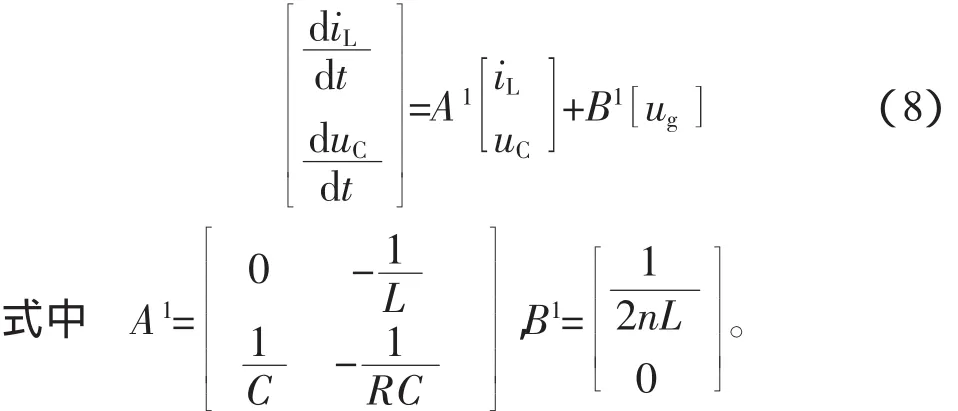
输入量、输出量的关系为

1.2 工作模态2

工作模态2原理如图3所示。当IGBT1、IGBT2均关断时，变压器二次侧由于上下两电感异名端并联且完全耦合，可相互抵消，因此可等效为导线[3]。

图3 工作模态2原理

依据分析模态1的分析方法，对图3所示回路列KVL方程

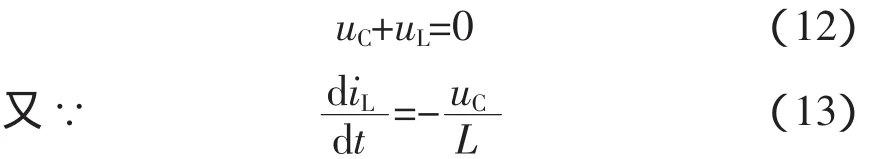
可得矩阵方程

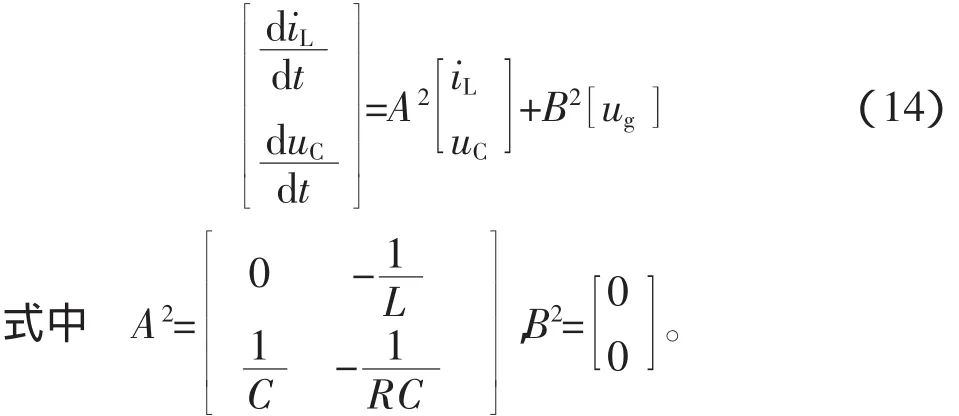
输入量、输出量之间的关系为

可得矩阵方程

静态工作点方程为

通过解静态工作点方程式得到

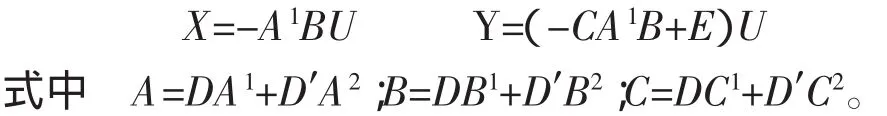
计算可得状态平均系数矩阵

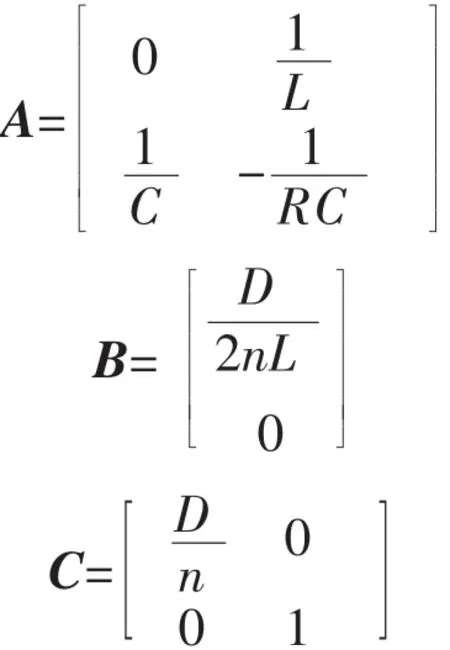
静态工作点矢量

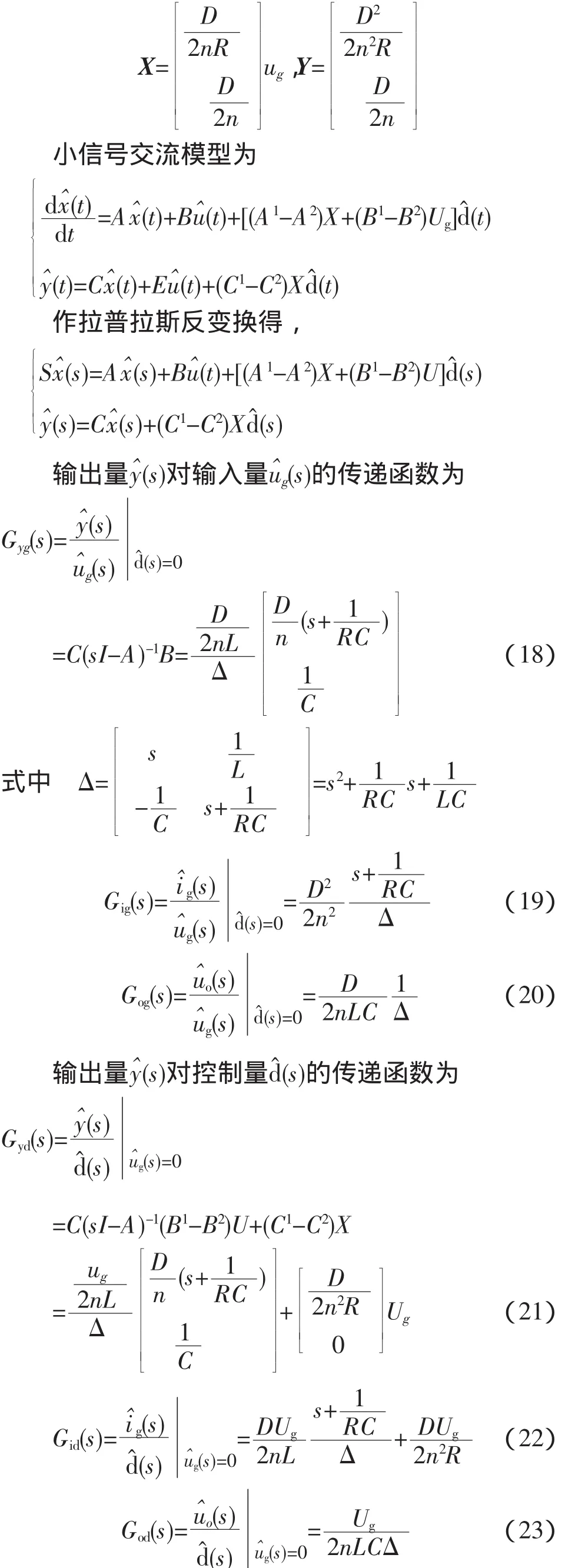
统一电路模型如图4所示。

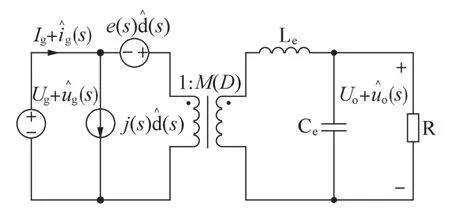
图4 统一电路模型

2 逆变输出滤波器的设计[4]

在图1中，忽略电感电阻和线路阻抗，滤波器输出电压相对于逆变桥输出电压的传递函数为

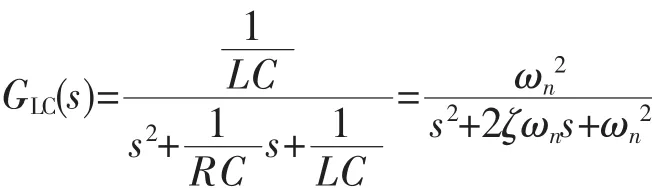
影响滤波效果的参数主要是转折角频率ωn和阻尼比ζ。选择逆变器的输出LC滤波器的转折频率fn（其中fn=）远远低于开关频率fs，它对开关频率以及其附近频带的谐波具有明显的抑制作用。在本设计中，开关频率fs=20 kHz，本设计选L=250 μH，C=18 mF，既保证了电感电流连续又能满足抑制谐波的需要。

3 PI控制参数设计

系统的控制框图如图5所示。其中Kpwm=为逆变桥的增益，这里n取4.5。Ug的最大值需考虑到逆变之前进行的整流输入电网电压波动及输入交流电压的有效值与整流滤波后所得直流电压之间的1.2倍关系。

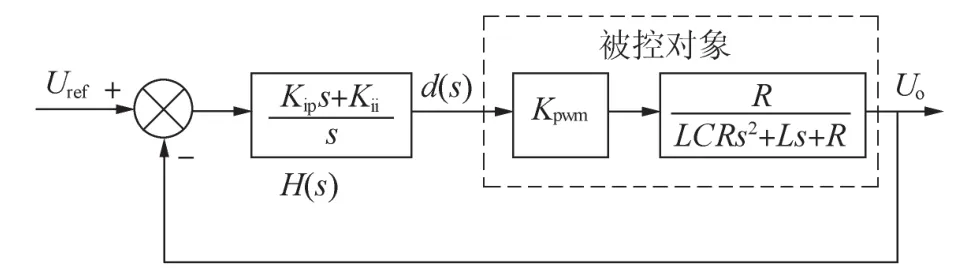
图5 弧焊逆变电源控制框图

本设计中电网电压设±10%的波动，纹波电压8%，电压摆幅为 Δu=1.2×10%U+8%×U=51.3 V，R/(LCRs2+Ls+R)为忽略电感L、电容C的寄生电阻后的LC滤波器传递函数，H(s)为PI调节器。

滤波器的转折频率fn=，把PI控制器的2零点设置在滤波器的转折频率处，即fz==fn，补偿后的穿越频率为转折频率的1/10，所以fc=0.1fn。

补偿后开环的传递函数为

由于在穿越频率处，回路增益为1，结合转折频率公式得到

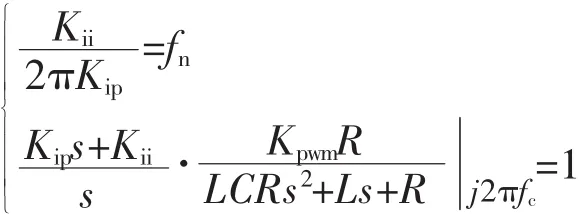
式中 R=0.164 Ω，L=250 μH，C=18 mF，Kpwm=30.14，解得 PI控制器的参数：Kip=3.29×10-3，Kii=1.533。

4 仿真验证

在MATLAB中的Simulink里建立闭环控制系统的传递函数模型，如图6所示。比较图7和图8，可以看到补偿后的阶跃响应在振荡次数、超调时间以及超调量方面明显好于补偿前。

根据上面设计的内环PI控制器，画出系统补偿前后的波特图，如图9所示。曲线1、2、3分别为补偿前、PI控制器、补偿后的被控系统的幅频相频特性。补偿前在低频时增益为29.6 dB，在2 620 rad/sec穿越0 dB线，相位裕量仅为7.59°。补偿后带宽增加，相位裕量为91.6°，稳定性增强。

图6 闭环控制系统的传递函数模型

图7 补偿前闭环系统输出电压阶跃响应

图8 补偿后闭环系统输出电压阶跃响应

图9 系统补偿前后的波特图

：

[1]程松鹤，丁 喆，刘艳兵，等.基于DSP双闭环控制的弧焊逆变电源设计与仿真[J].电源技术，2011，11(35)：1406-