机翼伸展对低速飞行状态的影响*

陈亚楠 余本嵩 金栋平

(南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016)

机翼伸展对低速飞行状态的影响*

陈亚楠 余本嵩 金栋平†

(南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016)

变翼飞行器在飞行过程中因机翼构型、面积等发生变化，引起质量分布、惯性及气动特性发生相应改变，飞行动力学因此受到影响．基于Lagrange方程，本文首先建立变形机翼飞行器的动力学模型，简化后得到伸展变翼的纵向运动方程，并通过气动仿真获得伸展机翼飞行器的低速气动特性．然后，借助线性插值确定气动参数随翼展的变化关系，研究了伸展变翼过程对于飞行器平飞、爬升、俯冲和盘旋的作用．结果表明，因变翼过程中升阻系数改变，飞行器将发生变速沉浮运动，此时为保持飞行状态的稳定，需对飞行器加以控制．

变翼飞行器， 飞行动力学， 机翼伸展， 气动特性， 稳定性

引言

为使飞行器在不同的飞行任务和飞行状态中保持与之相匹配的气动特性，人们提出了伸展机翼、折叠翼、变后掠翼等不同形式的变翼飞行器［1］．与固定翼飞行器不同，变翼飞行器能以最优的气动特性满足不同飞行状态对于飞行动力学的要求．例如，在爬升、平飞、盘旋、俯冲和格斗等不同飞行状态，变翼飞行器会以不同的翼展构型来达到其相应的最优气动特性，高效率地执行飞行任务．可展机翼飞行器因机翼伸展或收缩使飞行器翼面构型发生改变，以致重心与气动中心变化，继而引起飞行器动力学特性的改变:当机翼伸展时，提高飞行器低速性能和着陆性能;当机翼收缩时，提高飞行器的机动性能．王盼乐等设计了一种螺旋传动机构来实现机翼的伸缩，从机翼伸展速度和机翼振动、滑块和滑轨间摩擦力及驱动功率等方面对伸展机构进行了动力学仿真，证明所设计的螺旋传动机构可作为伸缩机翼飞行器的变形方案［2］．张伟等设计了可伸缩的机翼结构，并对该伸缩机翼在伸展过程中的振动进行了实验研究，发现伸展速度对机翼的横向振动具有较大影响［3］．Obradovic和Subbarao考虑气动、惯性等随时间的变化，通过非定常涡格法确定气动力并求解六自由度的非线性运动方程，研究了微小型飞行器变翼过程的飞行动力学，分析了鸥型翼飞行器在对称变形、反对称变形及不对称变形过程中飞行状态及变翼驱动力和力矩等［4－5］．乐挺等建立了解耦并简化的Z型翼变体飞机纵向多体动力学方程，在机翼折叠角速度较小且忽略非定常气动效应情况下，对变形过程中不同机翼折叠角速度下变体飞机的纵向动响应进行了数值仿真．结果表明，折叠过程中气动特性的变化是影响飞机动态特性的主要因素，机翼折叠后飞机的速度和迎角增加且飞行高度有较大幅度下降［6］．

本文针对沿翼展方向可伸展的变翼飞行器，研究变翼伸展对于低速飞行(小于0．4 Ma)状态的影响．基于Lagrange方程建立带有发动机推力的可伸展变翼飞行器纵向动力学模型，通过涡格法获得变翼过程低速气动力参数，经二次曲线拟合获得机翼伸展长度与升力和阻力系数的对应关系，详细研究了变翼过程对于飞行状态的作用．

1 变翼飞行器纵向运动方程

设对称布局飞行器以飞行速度V在其纵向对称面内飞行，攻角为α，爬升角为θ，如图1所示．建立固结于地球的惯性坐标系o－xyz和机体坐标系ob－xbybzb，其中xb沿机身纵向并指向机尾，yb垂直于飞行器纵向对称面，zb位于飞行器纵向对称面内且由右手定则确定．机体坐标系原点相对惯性系位置和速度为R0和V0，飞行器质心C相对惯性系和机体系的位置矢量为Rc和rc．在惯性系中，飞行器质心速度可表示为

式中ω为机体系相对惯性系的角速度，vc为机体系下飞行器的质心速度．

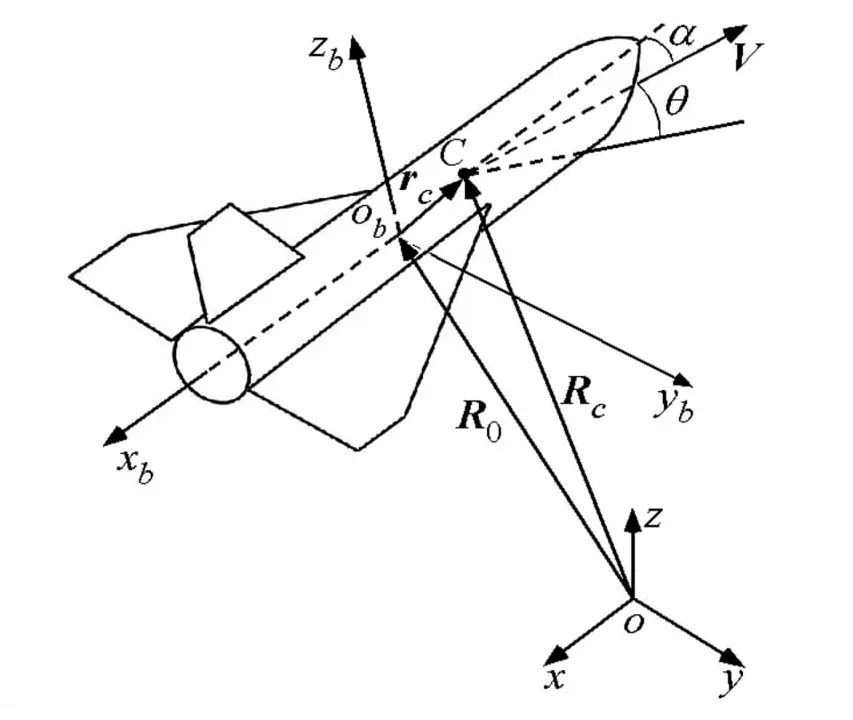
图1 机体坐标系与惯性坐标系Fig．1 The body－and Earth－fixed reference frames

飞行器在其全域Ω上的动能为

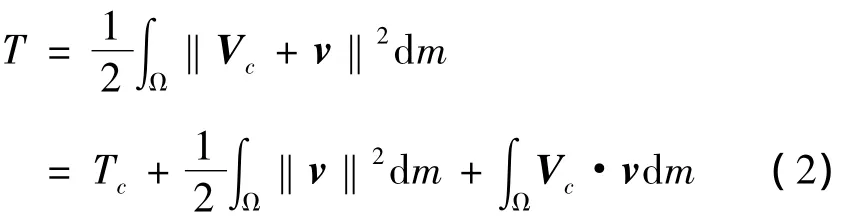
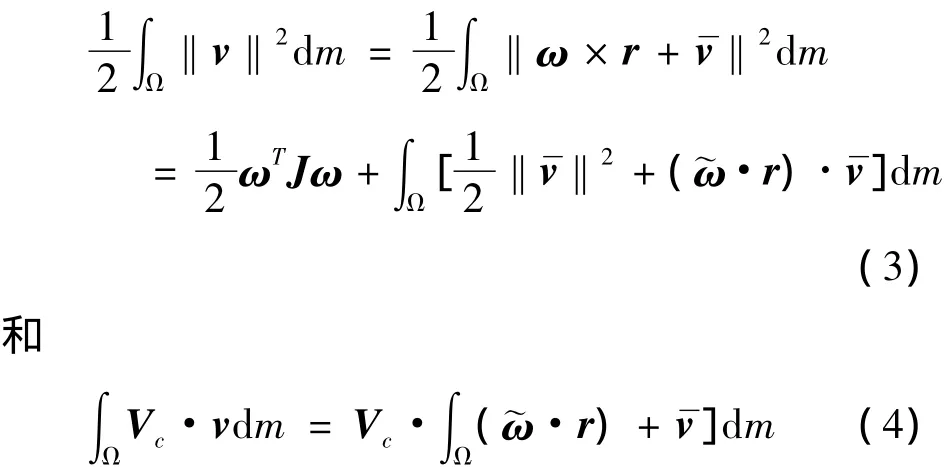
式中J和~ω分别为飞行器相对机体坐标系的惯量矩阵和反对称角速度矩阵．将式(3)和(4)代入式(2)，可得

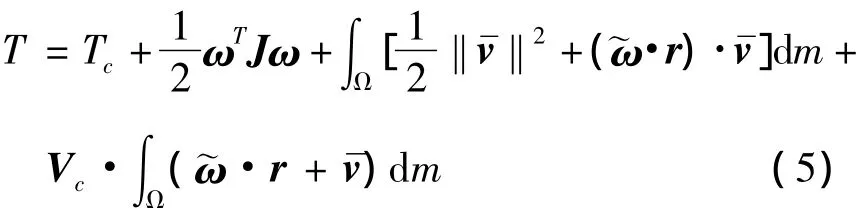
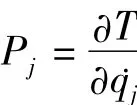
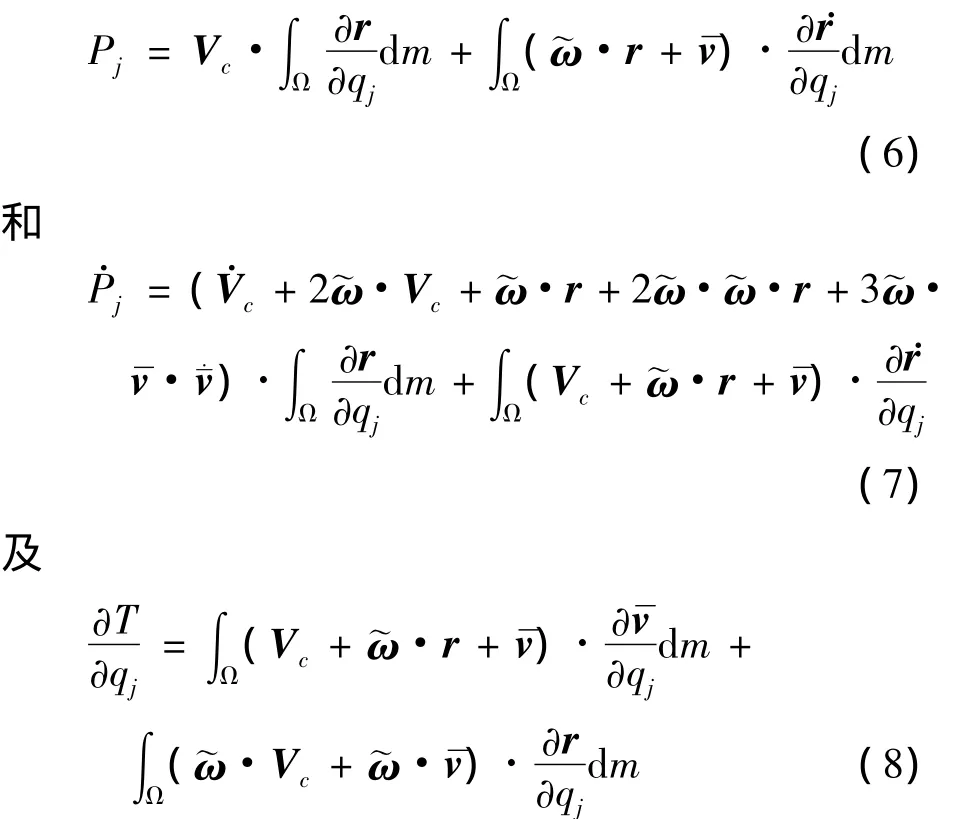
基于Lagrange方程，有

式中Qj为广义力．为简化上述方程，这里考虑纵向对称面内机翼匀速伸展的情形，如图2所示．假设质量为m的飞行器在密度为ρ的静止大气中飞行且发动机推力F沿机身方向．因而，可获得简化的纵向运动方程

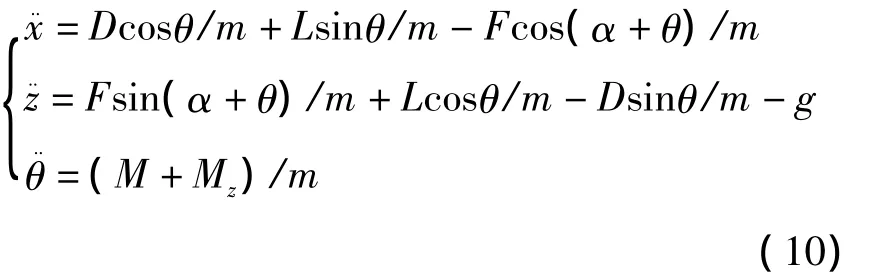
式中L=0．5CLρV2S、D=0．5CDρV2S和M=0．5CMρV2Sl分别为气动升力、阻力和力矩，CL、CD和CM为相应的升力、阻力和力矩系数，这里S和l分别为翼展面积和展长．Mz为飞行控制力矩，g为重力加速度．

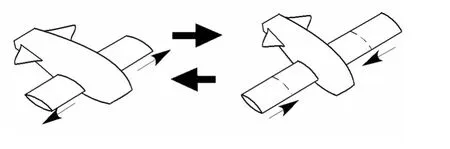
图2 机翼伸展示意图Fig．2 The sketch of planar deployable wing

2 气动模型

为认识变翼对飞行动力学的影响，需要获知作用于机翼的气动力．这里采用定常涡格法计算低雷诺数、低马赫数下固定展长的气动参数，然后根据线性插值获得气动参数随展长的变化关系．根据文献［7］对伸缩机翼气动特性的估算研究，采用固定展长的升力系数计算方法与CFD计算结果的最大相对误差仅为4．46%，能够有效反映展长变化时的情形．作为算例，本文采用双弧线翼型，翼型参数如表1所示．

表1 翼型参数Table 1 The parameters of airfoil profile

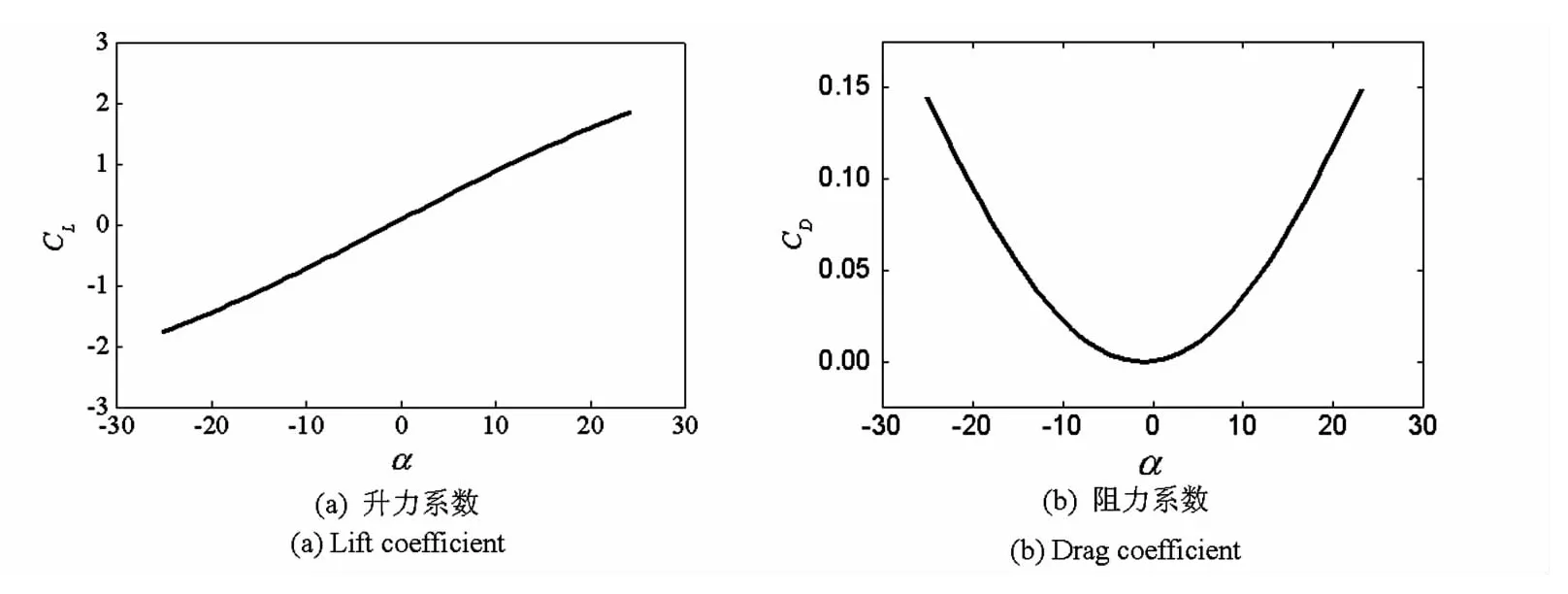
图3 机翼完全展开时的气动系数Fig．3 The coefficient of lift versus angle of attack with full scale wing

当机翼完全展开时，飞行器的升力参数计算结果如图3所示．从图3(a)可见，在一定的攻角范围内，升力系数与攻角近似成比例关系．

考虑攻角α=1°的情况，并设可展机翼飞行器基本参数如表2所示．由此可知飞行器升力系数和阻力系数随展长l变化的关系，如图4所示．通过二次曲线拟合，可得升力系数和阻力系数与展长的关系为

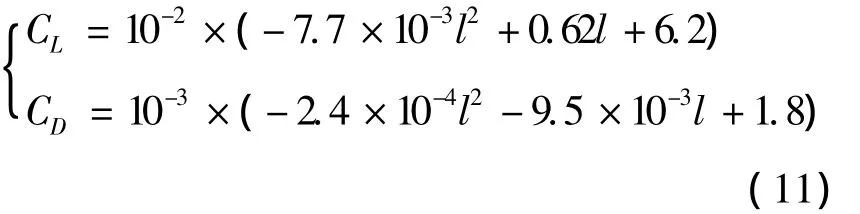
在上述气动模型的基础上，我们可研究飞行器在变翼过程中的飞行动力学行为．

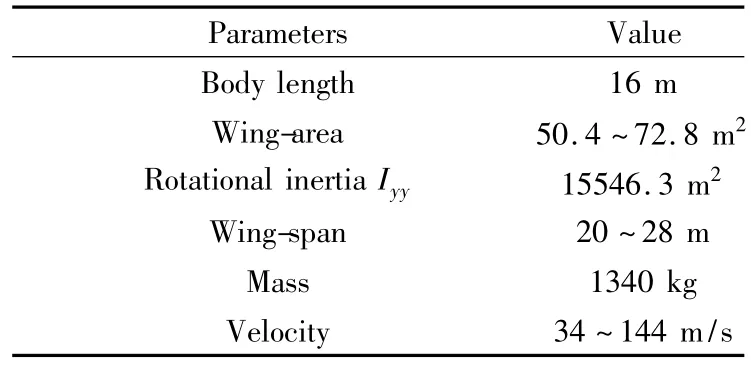
表2 飞行器参数Table 2 The parameters of aircraft

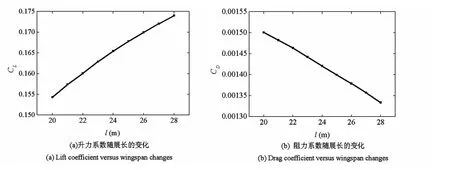
图4 气动参数随展长的变化Fig．4 The aerodynamic coefficients versus wingspan changes

3 变翼对飞行状态的影响

保持攻角 α =1°，取 ρ=1．29 kg/m3，g=9．8 m/s2．飞行器初始位于(x0，z0)=0，作平飞飞行 θ=0．初始平飞速度40 m/s、初加速度为零．设机翼以0．05 m/s的速度匀速收缩，并在Δt=80 s内完成变翼过程，发动机推力F=400 N．根据式(10)可计算变翼过程飞行器的飞行状态，结果如图5所示．从图5可见，机翼收缩使得飞行器沿水平方向作匀加速运动;在铅垂方向，因机翼收缩导致飞行器升力系数变小，由升力计算公式可知飞行器升力逐渐增大，以致飞行器发生加速沉浮运动．变形结束时沉浮运动速度为117．08 m/s，继而通过升力和阻力之改变而影响飞行状态．

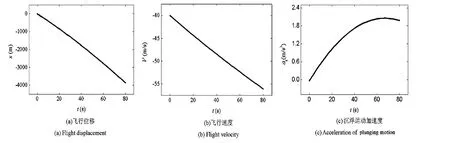
图5 变翼对平飞的影响Fig．5 The effect of wingspan change on level flight

对于匀速爬升情形．设机翼仍以0．05 m/s的速度收缩并在Δt=80 s内完成变翼过程，爬升角和发动机推力匀速增加，即θ=π/720rad/s和F=40N/s．其它条件为(x0，z0，θ0)=0，(x0，z0)=(－40 m/s，0)，初始发动机推力F0=900 N，计算结果如图6所示．图6(a)表明，飞行器以匀速增加的爬升角爬升时，最大速度并未出现在变形结束时刻．随着发动机推力的增大，飞行器速度不断增大，在此过程中重力和阻力沿机身的分力增大使得飞行器加速度减小，从而导致飞行器在后一阶段的速度减小．

对于俯冲情形．当机翼完全展开时，以固定攻角俯冲，即θ=π/18．设机翼收缩速度为0．5 m/s，发动机推力F=400 N，x=40 m/s，Δt=8 s．飞行速度和纵向加速度计算结果如图7所示．从图7(a)可见，俯冲时飞行器速度增加较快，为保证飞行器速度在102 m/s以内，机翼变形需在较短时间内完成．图7(b)表明，飞行器在俯冲过程中，铅垂方向会产生加速度，在变形结束时沉浮速度为15．22 m/s，继而通过升力和阻力之改变而影响飞行器的俯冲状态．

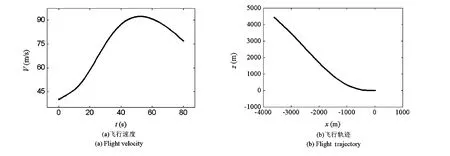
图6 变翼对爬升的影响Fig．6 The effect of wing－span change on climbing flight

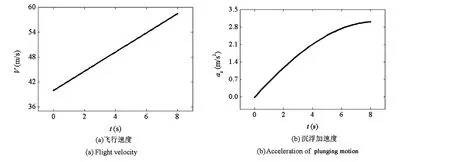
图7 变翼对俯冲的影响Fig．7 The effect of wing－span change on diving flight

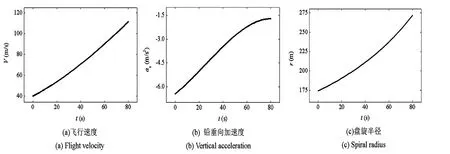
图8 变翼对盘旋的影响Fig．8 The effect of wingspan change on turning flight

对于盘旋情形．设机翼完全展开时以一定倾角α=π/180和速度盘旋，机翼收缩速度为0．05 m/s，θ0=π/9， θ=－π/1440 rad/s．其它参数设为x0=40 m/s，F0=900 N，F=15N/s，Δt=80 s．盘旋时飞行速度、铅垂方向加速度及盘旋半径变化如图8所示．图8(b)表明，铅垂方向产生了加速度，在变形结束时铅垂向速度为294．02 m/s，进而通过升力和阻力的改变而影响飞行器的盘旋运动．通常性能较好的飞行器盘旋半径约在300 m以内．从图8(c)可见，本算例得出的盘旋半径位于该范围内．

需要指出的是，由于所飞行控制力矩与飞行器重心、机翼压力中心等有关，在建立飞行器气动模型过程中，为使机身获得一定质量配比，只是给予其一定的总质量．因此，以上四个算例均未计算飞行器在变形过程中力矩的变化．在飞行器平飞、俯冲和盘旋过程中，若要飞行器在机翼构型发生较大改变时保持其飞行状态，则需沿铅垂方向施加控制以抑制变翼产生的加速度．显然，飞行器在变翼过程中，因升力系数和阻力系数的变化率不同以致飞行器在保持某个方向的飞行状态时，在另外的飞行方向会产生加速运动，因此需要对变翼飞行器进行稳定性控制．比如，若要始终维持飞行器的平飞状态，则需要不断调整飞行器的攻角．

4 结论

通过建立变翼飞行器的动力学模型，研究了可展机翼飞行器在低速气动力作用下的飞行动力学问题，包括平飞、俯冲和盘旋时的动力学响应计算．数值计算表明，采用基于定常涡格法的气动力来分析变翼对于飞行状态的作用，结果与实际飞行情况相一致．在飞行器变翼过程中，若要保持其原有飞行状态，则需对飞行器进行稳定性控制．注意到，更准确的动力学建模是基于柔性机翼模型，可能带来变翼过程更加复杂的非线性动力学行为，比如颤振、失速等问题．此外，高超声速下飞行器结构与气动相互耦合动力学是一项值得研究的重要问题．

1 Wlezien R W，Homer G C，McGowan A R，Padula S L，Scott M A，Silcox R J，Simpson J O．The aircraft morphing program．AIAA Journal，1998，98(1297):20～23

2 王盼乐，赵美英，严子焜．伸缩机翼变形机构多柔性体动力学仿真分析．科学技术与工程，2009，9(13):3708～3712(Wang P L，Zhao M M，Yan Z K．Analysis of stretching deformation of the spiral wing drive mechanism many flexible body simulation．Science Technology and Engineering，2009，9(13):3708～3712(in Chinese))

3 张伟，张谦，曹东兴．可伸缩机翼结构设计与振动实验研究．动力学与控制学报，2011，9(4):326～330(Zhang W，Zhang Q，Cao D X．Structural design and vibration experimental investigation of telescoping wings．Journal of Dynamics and Control，2011，9(4):326 ～ 330(in Chinese))

4 Obradovic B，Subbarao K．Modeling of flight dynamics of morphing－wing aircraft．Journal of Aircraft，2011，48(2):391～401

5 Obradovic B，Subbarao K．Modeling of dynamic loading of morphing－wing aircraft．Journal of Aircraft，2011，48(2):424～435

6 乐挺，王立新，艾俊强．Z型翼变体飞机的纵向多体动力学特性．航空学报，2010，31(4):679～686(Yue T，Wang L X，Ai J Q．Longitudinal multibody dynamic characteristics of Z－wing morphing aircraft．Acta Aeronautica et Astronautica Sinica，2010，31(4):679～686(in Chinese))

7 孙殿杰，谷良贤，龚春林．伸缩翼气动特性估算方法研究．飞行力学，2012，30(1):13～16(Sun S J，Gu L X，Gong C L．Investigation of an aerodynamic characteristic evaluation method for the deformable wing．Flight Dynamics，2012，30(1):13～16(in Chinese))

*The project supported by the National Natural Science Foundation of China(91016022)，Program for Changjiang Scholars and Innovative Research Team in University(IRT0968)，and the Fundamental Research Funds for the Central Universities(NS2012034)

† Corresponding author E－mail:jindp@nuaa．edu．cn

THE EFFECT OF WINGSPAN CHANGE ON LOW SPEED FLIGHT OF A MORPHING AIRCRAFT*

Chen Yanan Yu Bensong Jin Dongping†
(State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics，Nanjing210016，China)

The flight dynamics of a morphing aircraft is obviously depended on the wing shape，because it results in different aerodynamic properties due to the mass reallocation and inertia change．This paper studies the flight dynamics of a changeable wingspan aircraft in low speed flight．Starting with the modeling of the morphing aircraft on the basis of Lagrange＇s equation，a set of longitudinal dynamic equations for a planar deployable wing is established．At the same time，the low speed aerodynamic parameters for fixed wingspan are calculated with the vortex lattice method．Afterward，the corresponding aerodynamic coefficients versus the wingspan changes are determined through the use of linear interpolation method．The effect of wingspan changes on the flight dynamics of the simplified morphing aircraft are analyzed for different flight status such as level flight，climbing，diving and turning．The results show that wingspan change would influence the flight status of morphing aircraft especially in the longitudinal flight so that the relevant control must be taken in order to keep the stability of the flight of a morphing aircraft．

morphing aircraft， flight dynamics， deployable wingspan， aerodynamic property， stability

15 June 2012，

6 July 2012．

10．6052/1672－6553－2013－051

2012－06－15 收到第 1 稿，2012－07－06 收到修改稿．

*国家自然科学金(91016022)、长江学者和创新团队计划(IRT0968)、高等学校基础研究(NS2012034)资助项目

E－mail:jindp@nuaa．edu．cn